对称结构复模态向量的二阶泰勒展开

张文丹

（长春理工大学 理学院，长春 130022）

模态是一个机械结构的固有振动特性，它可以完整地描述一个结构的动力特性。每一个结构都具有特定的固有频率、阻尼比和模态振型，根据模态频率及模态向量等模态参数是实数还是复数，模态可分为实模态和复模态。工程应用中针对阻尼系统的结构优化和模型修正经常会用到复模态向量［1，2］，但目前多数研究只是使用复模态向量的一阶泰勒展开式［3，4］，关于复模态向量的二阶泰勒展开式的研究很少有文献提到。文献［5］中提出了关于复频率的一阶导数，但是复频率的二阶导数算法的讨论却很少出现。显然，在对复模态向量进行泰勒展开时，其一阶泰勒展开和二阶泰勒展开时的近似精度是不一样的。文献［6，7］中提出了多元向量值函数的高阶导数及一、二阶泰勒展开的理论，文献［8］中提出了求解实模态特征值和特征向量的一、二阶导数的算法，虽然此算法是无阻尼求解问题，但是对阻尼系统的相关研究有一定的推广价值。关于文献［9］中提出的相容性条件方程，为求解特征值的高阶导数提供了方便，其导出的算法公式，简洁紧凑、易于理解且编程方便。本文在这些研究的基础上提出了对称结构复模态向量的二阶泰勒展开算法，算例证明此算法的正确性及有效性。

1 多元向量值函数的一阶及二阶泰勒展开

u=(u1(b),…,uN(b))T每一维分量皆是向量b=(b1,…,bq)T的函数，因此u=(u1(b),…,uN(b))T是多元向量值函数，如果u=(u1(b),…,uN(b))T第i维分量 ui(b1,b2,…,bq)(∀i=1,2,…,N)的梯度向量为［6］

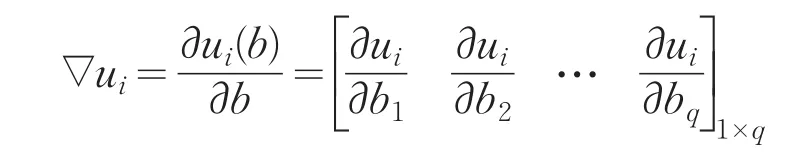
那么，它的梯度矩阵为

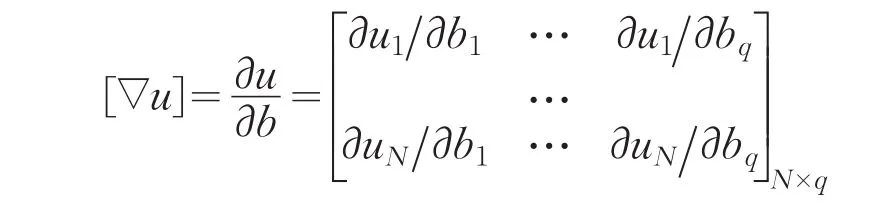
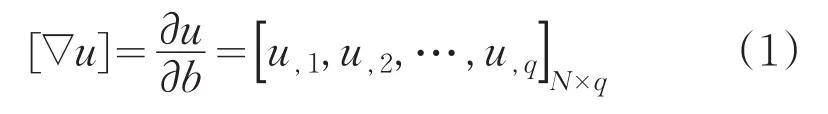
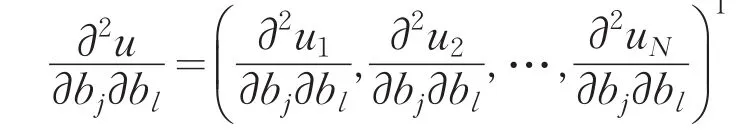
那么海森矩阵还可改写为［7］

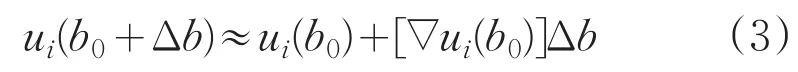
二阶泰勒展开形式为

2 复模态向量的一、二阶泰勒展开式

2.1 复模态参数

描述自由度为N的线性阻尼离散系统的自由振动方程为

式中M、C和K∈RN×N分别为对称的质量、阻尼和刚度矩阵，即该系统为对称系统。结构有限元分析时，作拉普拉斯变换 x(t)=uewt=uejωt(w=jω )代入(5)式可得(w2Mu+wCu+Ku)ewt=0。考虑阻尼时的系统极点及复模态对( )

si,ui(i=1),2,…,2N 满足方程

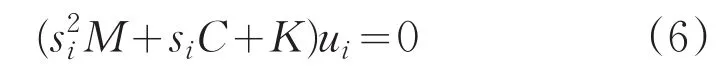
对于N自由度振动系统，特征方程det[s2M+sC+K]=0有2N个呈复共轭对出现的特征 值 s1,s2,…,s2N(其 中 si+1为 si的 共 轭（i=1,3,…,2N-1）)，该特征值又称为复频率。每个复频率对应着一组呈复共轭对出现的特征向量ui（ui∈CN），则ui称为系统(5)与 si相对应的第i个模态向量，这里将u1,u2,…,u2N(其中ui+1为ui的共轭（i=1,3,…,2N-1）)又称为复模态。如果系统的特征值全不相同，那么称之为单特征系统，对单特征系统，则存在规范正交关系为［10］

其中状态向量矩阵为 Φ=[φ1,φ2,…,φ2N]，状态向量为

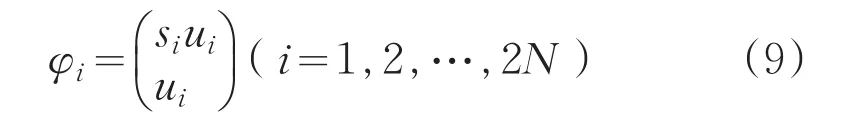
且

所满足的广义特征方程为

2.2 复模态向量的梯度矩阵的算法

值函数的有关理论。由（9）式可知，状态向量的后N维即构成系统的复模态向量，更由于阻尼的影响，使系统（5）的复模态的特征导数不能像无阻尼实模态的特征导数分析那样，在实模态空间中进行［6］，为此考虑引入状态空间来实现这一目标。定义状态向量φi关于对第 j个参数bj的一阶导数为

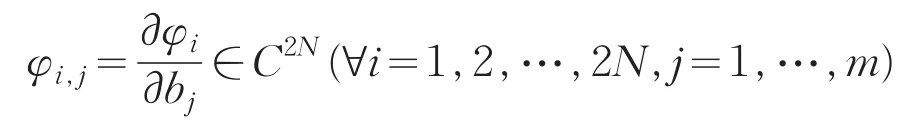
对于对称的单特征系统来说，根据文献［11］中提供的方法，将状态向量的一阶导数φi,j(j=1,…,q)在状态空间内表示为基底的某一线性组合，即

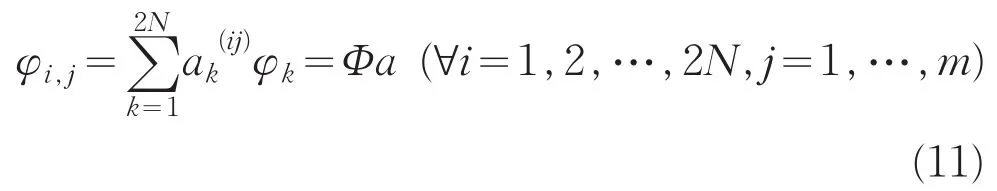
其中 φk(∀k=1,2,…,2N)是广义特征问题（10）式的状态空间的基底，是（11）式中的一阶线性组合系数。由（11）式可知

利用（11）式所具有某些数学性质来求解一阶线性组合系数，并代入（12）式，即可确定复模态向量的一阶导数，并由（1）式获得其梯度矩阵。

将(10)式两边对第 j个参数bj求导得

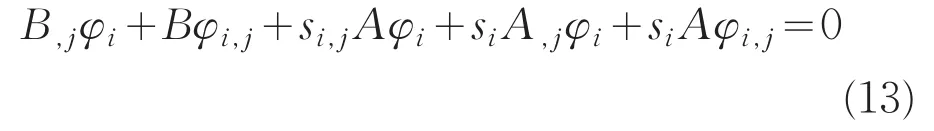
其中

整理(13)式得一阶导数φi,j的支配方程为

将(11)式代入支配方程，并左乘ΦH得

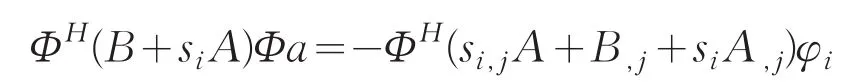
用状态向量之间的规范正交化关系（7）和(8)式解耦支配方程，即可析出一阶线性组合系数的控制方程如下

由第i个以外的方程可解得2N-1个一阶线性组合系数为

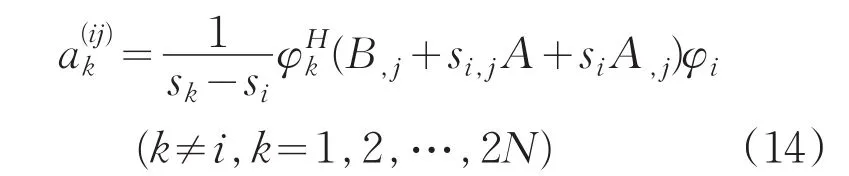
根据正交化条件 φkTAφi=0(k≠i)，（14）式可简化为

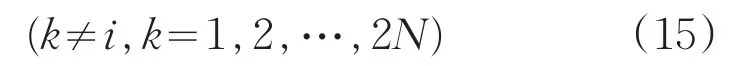
同时由于一阶线性组合系数的控制方程的相容性［9］，根据其相容性条件方程可得

因此解得复频率的一阶导数为

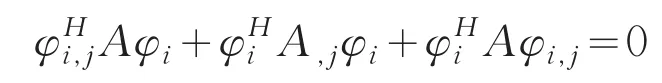
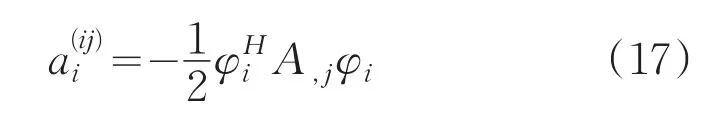
将（15）和（17）式的一阶线性组合系数化为N维空间形式为

代入（12）式就可求得复模态的一阶导数，再代入（1）式即可获得梯度矩阵。

2.3 复模态向量的海森矩阵的算法

将特征方程(10）对设计参灵敏bj求导得

再对设计参数bl求导得

整理上式得φi,jl的支配方程为

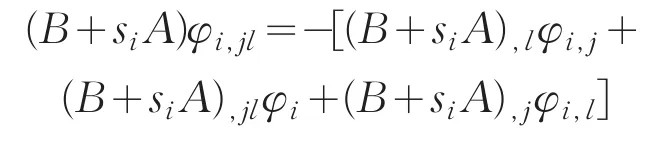
将(19)式代入支配方程，并左乘ΦH，用状态向量之间的规范正交化关系（7）和(8)式解耦支配方程，即可析出二阶线性组合系数的控制方程如下

由第i个以外的方程可解得2N-1个二阶线性组合系数为

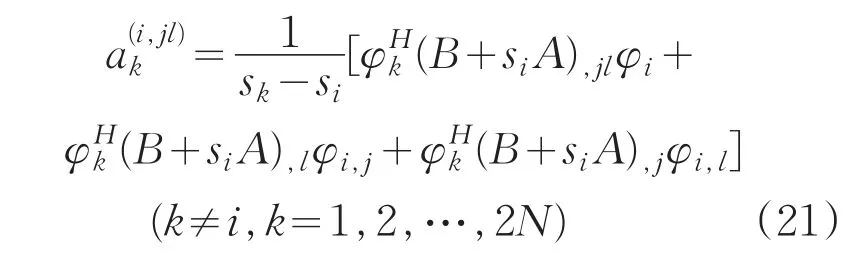
其中，

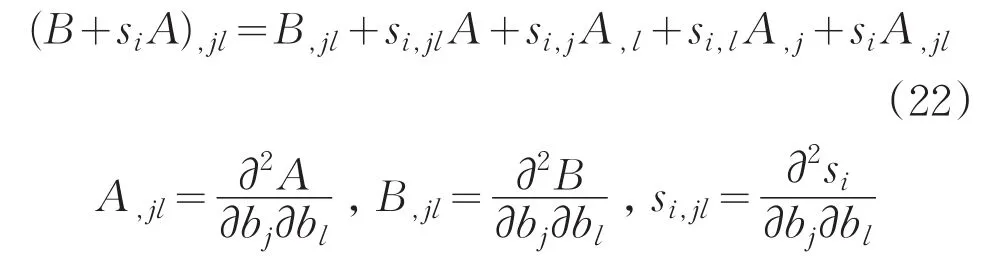
同时由于二阶线性组合系数的控制方程的相容性［9］，根据其相容性条件方程可得

可解得复频率的二阶导数为

其中si,l和ϕi,l可用与si,j和ϕi,j同样的算法求得。

关于bl求二阶导数得

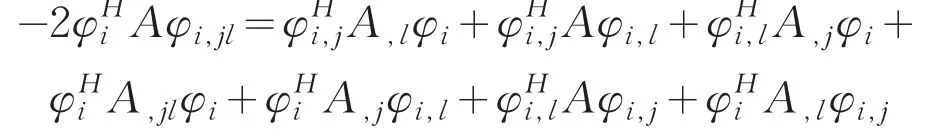
将（19）式代入上式即有

将（21）和（24）式代入（20）式就可求得复模态的二阶导数，再代入（2）式即可获得海森阵。

2.4 复模态向量的一、二阶泰勒展开式

由（18）式计算得到一阶线性组合系数代入（12）式，再代入（1）式即可构成第i阶复模态的梯度矩阵[∇ui]，再代入（3）式，获得系统（5）的第i阶复模态在处受到设计参数发生扰动量为的扰动后用一阶泰勒展开式得到的近似值。

将由（21）和（24）式计算得到的二阶线性组合系数代入（20）式，再代入（2）式即可构成第i阶复模态的海森矩阵[∇2ui]，再代入（4）式，获得系统（5）的第i阶复模态在处设计参数发生扰动量为的扰动后的用二阶泰勒展开式得到的新值。

3 数值算例

3.1 算法步骤

（1）输入系统参数b；

（2）构造对称系统的质量M、阻尼C和刚度矩阵K，此时b取初值b0；

（3）构造矩阵A、B；

（4）计算复模态参数si和ui；

（5）利用公式（15）和公式（17）求2N 个一阶灵敏度系数；

（7）利用公式（21）和公式（24）求2N 个二阶灵敏度系数；代入得到复模态的二阶灵敏度，即二阶导数，构成海森矩阵；

表1 计算所得结果

（8）将步骤（6）和（7）得到的梯度及海森阵代入公式（4），得到ui(b0+Δb)的二阶泰勒近似值；

（9）在系数参数取为b0+Δb时重新计算步骤（2）、（3）、（4），得到 ui(b0+Δb)，与公式（4）得到的近似值相比较。

3.2 数值算例

如图1所示，有阻尼的弹簧质量系统，如果m1=m2=m3=m，k1=k2=k3=k，

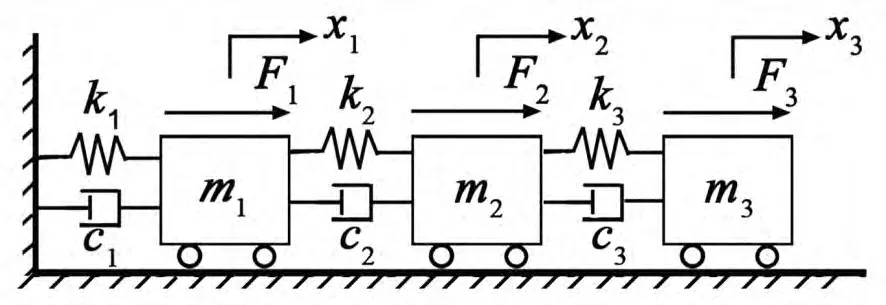
图1 弹簧质量系统

则该对称系统的质量M、阻尼C和刚度矩阵K分别表示为

本文取k2作为设计参数，为了更好地展示算法的可行性，在求二阶导数时，仍取为k2为设计参数，初始系统参数m1=m2=m3=1.0kg；c1=10.0N/(m⋅s-1),c2=10.0N/(m⋅s-1),c3=10.0N/(m⋅s-1) ；k1=k2=k3=100N/m及设计参数的初始值b0=(k2,k2)T，及设计参数第一次的扰动量及第二次扰动量 Δb=(Δk2,Δk2)T，取 Δk2=-5。计算所得的结果见表1。

由表1的第3列与第5列可知，复频率的二阶导数及复模态的二阶导数由本文算法计算与差分算法的计算结果差距不大，说明了本文算法的正确及有效性。再由表1的第6列可知，本文算法的计算结果可用于替代设计参数发生扰动后的复模态新值，精度与差分在该步长下的精度基本一致。

4 结论

本文首先根据相容性条件方程理论，给出了系统复频率的二阶导数的算法，然后给出了系统复模态的二阶导数算法，特别是利用了单特征系统的对称性解决了其线性组合系统控制方程组降秩的问题。再利用多元向量值函数的泰勒展开式理论，建立了系统复模态向量在某点处作泰勒近似的方法。为复模态向量应用于模型修正及结构优化等领域来提高模型精度提供了新的算法基础。数值算例说明了本文算法的有效性和正确性。

［1］殷磊，陈科，陈振华.轧钢机主传动系统的复模态分析［J］.机械传动，2014，38（6）：114-118.

［2］王刚，王远，周文松.轧钢机主传动系统的复模态分析［J］.地震工程与工程振动，2013，33（4）：89-94.

［3］于澜，张任，乐明锋，等.模态参数的灵敏度分析在结构工程领域中的应用［J］.长春工程学院学报：自然科学版，2012，13（3）：1-3.

［4］杨佑发，赵忠华，徐典.基于改进模态参数灵敏度法的结构损伤识别研究［J］.地震工程与工程振动，2011，31（1）：95-100.

［5］Sondipon A，Friswell MI.Eigenderivative analysis of asymmetric non-conserva-tive systems［J］.International Journal for Numerical Methods in Engineering，2001，51(6)：709-733.

［6］张淼.实模态向量梯度算法［J］.长春工业大学学报：自然科学版，2013，34（5）：551-554.

［7］张淼.非对称结构振型向量的海森阵算法及应用研究［J］.长春工业大学学报：自然科学版，2014，35（2）：216-220.

［8］张淼.结构实模态参数的高阶灵敏度算法［J］，长春工程学院学报：自然科学版，2014，15(1)：122-125.

［9］张淼，于澜，鞠伟.重频系统的频率灵敏度分析算法研究［J］.华南师范大学学报：自然科学版，2014，46（3）：39-43.

［10］张淼，鞠伟.计算各种振系模态灵敏度的统一算法［J］.长春工程学院学报：自然科学版，2012，13（4）：119-122.

［11］张淼，鞠伟.基于松驰技术的结构模态敏感性分析［J］.长春理工大学学报：自然科学版，2012，35（4）：157-160.