基于圆阵的超波束技术
2014-12-07徐伟东章新华郑文强
徐伟东,章新华,周 敏,郑文强,李 澍
(海军大连舰艇学院 水声信息研究中心,辽宁 大连116018)
0 引 言
目前,圆柱阵被广泛应用于现代被动声呐系统。被动声呐系统最主要的工作是对水声目标进行方位估计,主要通过采用常规波束形成(Conventional Beamforming,CBF)技术来实现,它有容易实现、鲁棒性强和对于相干信号不敏感的优点[1]。但随着潜艇隐身技术的发展,它方位分辨率较低的不足,使其难以有效探测水下目标。如何提高声呐系统的方位分辨率,提高对弱目标的探测能力成为了目前迫切解决的问题之一。
当前对于如何提高圆柱阵声呐的方位分辨率和水下弱目标的探测能力,主要有2 种方法,传统的方法是放大基阵尺寸,增加阵元数量,这种方式可以有效的增强声呐的方位分辨率,但是一般情况下受运载平台的限制,基阵尺寸难以扩大。另一种方式,也是目前水声领域研究的热点,是通过改进信号处理算法,在基阵尺寸一定的条件下,提高声呐系统的方位分辨率已经对弱目标的探测能力[5]。目前在较为普遍的做法是采用自适应算法,提高声呐的方位分辨率[5]。但是自适应算法也存在着计算量大,鲁棒性弱得不足。目前在国外已有人提出一种基于 CBF和分裂波束的超波束技术(Hyper Beamforming,HBF),它可以有效的抑制波束旁瓣,提高声呐的方位分辨率[2-3]。在国内,上海船舶电子设备研究所的周胜增已研究在线阵上采用HBF的技术。但是在圆柱阵上的HBF 技术应用研究还未有人着手。
1 算法原理
1.1 基于圆阵的常规波束形成
图1 给出了一个平面的均匀间隔的圆阵,其半径为r,阵元数为M,按顺时针方向依次为H1,H2,…,HM,把圆心O 通过阵元H1的方向设定为0°方向,阵元间距为a = 2π/M。

图1 圆阵几何模型Fig.1 Gemetry model of circular array
如果基阵在t 时刻接收到的信号为X(t)=[x1(t),x2(t),…,xM(t)]H,基阵的阵列流型W =[w1,w2,…,wi,…,wM]H,wi= e-jτi,τi是阵元Hi相对于O 点的延时,可表示为

1.2 基于圆阵的超波束的原理
通常我们利用声呐基阵,阵元信号在参加波束形成时的原始形式加以处理,提高声呐的方位分辨率。通过借鉴分裂波束的思想,基阵均等的分为2个均等的子阵,同时生成2个波束,再进行相关处理。采用这种这种方式可以使分辨精度接近克拉默—拉奥下界[5]。
在图2 中,将阵元个数为2N的某段基阵均等分为左右2个子阵,子阵的阵元数均为N。同时利用CBF 方法分别利用左右子阵在相同方向上输出2个波束,分别记为左波束Rl和右波束Rr。如图2所示。

图2 圆阵的分裂波束示意图Fig.2 Split beam of circular array
HBF 在CBF 产生的子波束的基础上,对左右子阵产生的左右波束Rl和Rr采取包括绝对值运算、和运算、差运算、加权运算、系数选择等处理,生成超分辨波束。HBF 算法主要步骤如下:
1)将基阵均等分为左右2个子阵,利用CBF算法生成左波束Rl和右波束Rr。
2)对左右波束分别取绝对值后采取加计算得到“和”波束RS=| Rl| +| Rr|。
问题银行市场化退出的关键是解决好“触发标准”。仅仅依靠“不能清偿到期债务”或“已经或可能发生信用危机”等定性标准来启动问题银行的风险处置,可能错过最佳救助时机,导致问题更加严重。可以借鉴国际监管经验,将可量化的风险处置标准,如银行的资本充足状况,引入风险处置相关法律条文,增强问题银行风险处置的科学性和可操作性。
3)对左右波束采取减计算后做绝对值处理得到“差”波束RD=| Rl-Rr|。
4)选取合适的超波束指数n。其中0.3 <n <1[6]。
5)通过加权计算得到超波束输出RH=|-|1/n。
2 仿真分析
接收阵采用32 条阵元均匀排列的圆阵,半径r = 0.8 m,声速c =1 500 m/s。假定目标信号频率为5 000 Hz,方位为0°,选取超波束系数n =0.5。分别用CBF和HBF 预生成波束。
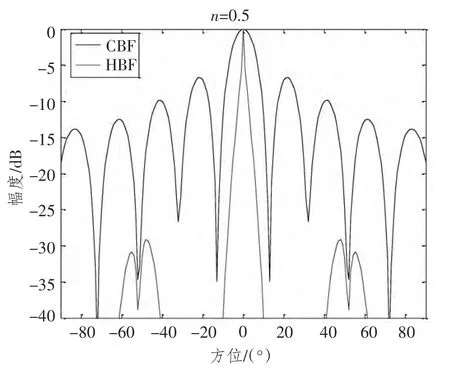
图3 CBF和HBF 指向性图Fig.3 Directed graph of CBF and HBF
从图3 可以看到,HBF的主瓣宽度比CBF 更窄,旁瓣幅度也减少了20 dB。通过分析可知,得出HBF 可有效减小主瓣宽度,抑制旁瓣幅度。
设置超波束指数n为{0.3,0.5,0.9 },分别在0°方向预成波束。

图4 超波束指数n=0.3,0°方位Fig.4 Hyper beam index n=0.3,direction is 0°

图5 超波束指数n=0.5,0°方位Fig.5 Hyper beam index n=0.5d,irection is 0°
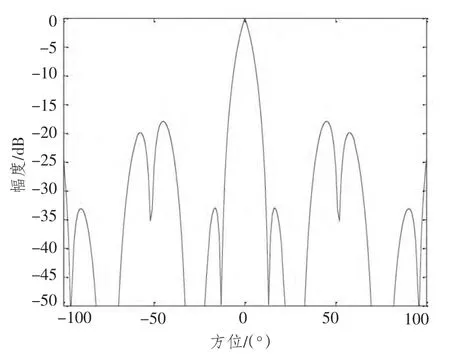
图6 超波束指数n=0.9,0°方位Fig.6 Hyper beam index n=0.5,direction is 0°
通过分析图4~图6 可以发现,在n =0.3 时,波束的旁瓣较n =0.5 时至少降低了15 dB,较n =0.9 时至少降低了25 dB。主波束的宽度也至少随着超波束指数n的减小而减小。
假定目标信号为2个不同强度的单频余弦信号,频率为{5 000 Hz,4 900 Hz},背景噪声为各向同性高斯白噪声,目标方位为{30°,17°},目标强度为{-5 dB,-13 dB},{-5 dB,-15 dB},{-5 dB,-18 dB},超波束指数n 取0.3,在-45°到45°方向上生成均等分布的128个波束。
图7 中,当弱目标强度为-13 dB 时,CBF和HBF 都能发现目标,但是HBF的情况好于CBF。图8 中弱目标强度为-15 dB 时,CBF 中的弱目标开始被噪声掩盖,但HBF 仍然能够清晰发现目标。图9中,CBF 中的弱目标已经完全被噪声掩盖,但HBF仍然能够发现目标,说明HBF 可以有效提高对弱目标的探测能力。

图7 目标1:强度-13 dB,方位15°;目标2:强度-5 dB,方位30°Fig.7 Target 1:intensity is-13 dB,direction is 15°;target 2:intensity is-5 dB,direction is 30°

图8 目标1:强度-15 dB,方位15°;目标2:强度-5 dB,方位30°Fig.8 Target 1:intensity is-15 dB,direction is 15°;target 2:intensity is-5 dB,direction is 30°

图9 目标1:强度-19 dB,方位15°;目标2:强度-5 dB,方位30°Fig.9 Target 1:intensity is-19 dB,direction is 15°;target 2:intensity is-5 dB,direction is 30°
假定目标信号为2个不同强度的单频余弦信号,频率为{5 000 Hz,4 900 Hz},背景噪声为各向同性高斯白噪声,阵元输入信噪比为{-5 dB,-15 dB},入射方向为{20°,0°},{20°,10° },{20°,15° },超波束指数n 取0.3,在-45°到45°方向上生成均等分布的128个波束。
在图10 中,在弱目标与强目标间隔20°时HBF和CBF 都能有效发现目标,但是CBF 目标强度不明显。在图11 中,强弱目标间隔为10°时,CBF 中的弱目标基本被强目标掩盖,而HBF 仍然能够有效发现目标。在图12 中,强弱目标间隔5°时,CBF 中弱目标被强目标完全掩盖,而HBF 仍然能够有效发现目标。通过分析可以得出结论,HBF 可以有效提高对于2个相邻不同强度目标的方位分辨率。在保持其他条件不变的基础上,将目标信号的目标信号方向改为{10°,20°},目标信号的强度改为{-5 dB,-5 dB}。

图10 目标1:强度-15 dB,方位0°;目标2:强度-5 dB,方位20°Fig.10 Target 1:intensity is-15 dB,direction is 0°;target 2:intensity is-5 dB,direction is 20°

图11 目标1:强度-15 dB,方位10°;目标2:强度-5 dB,方位20°Fig.11 Target 1:intensity is-15 dB,direction is 10°;target 2:intensity is-5 dB,direction is 20°
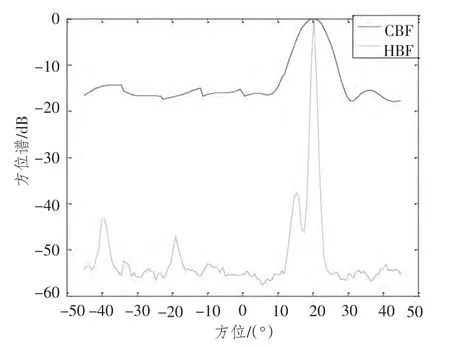
图12 目标1:强度-15 dB,方位15°;目标2:强度-5 dB,方位20°Fig.12 Target 1:intensity is-15 dB,direction is 15°;target 2:intensity is-5 dB,direction is 20°

图13 目标1:强度-5 dB,方位1°;目标2:强度-5 dB,方位20°Fig.13 Target 1:intensity is-5 dB,direction is 10°;target 2:intensity is-5 dB,direction is 20° targets
通过图13 可以清楚地看到,在两同强度目标信号间隔10o的情况下,CBF 已经无法有效分辨2个目标,而HBF 仍可以有效分辨。从而可以得出结论HBF 可以有效提高圆阵对同强度相邻目标的方位分辨率。
3 结 语
本文在介绍了圆阵的CBF 算法和分裂波束基本原理的基础上,给出了基于圆阵的HBF 算法和运用。通过仿真分析CBF与HBF的指向性图和不同超波束指数下HBF的指向性图。得出结论HBF 可以有效的减小波束主瓣宽度和抑制旁瓣,并且这种能力是随着超波束指数的减小而加强的。通过仿真分析,CBF和HBF 对于不同强度弱目标的方位谱图,相邻同强度和不同强度弱目标的方位谱图。得出结论HBF可以有效提高圆阵的弱目标探测能力和方位分辨率。
[1]周浩.基于MVDR 自适应波束的高分辨方位估计[J].武汉理工大学学报,2009,23(4):118-121.ZHOU Hao,High resolution DOA estimation algorithms based on MVDR beam former outputs[J].Journal of Wuhan University of Technology,2009,23(4):118-121.
[2]RAMA P.Krushna.Side lobe suppression of concentric circular arrays using non conventional beam forming technique[J].International Journal od Modern Engineering Research,2012,3(5):635-638.
[3]周胜增.超波束在被动声呐频谱分析中的应用[J].声学技术,2010,5(10):460-462.ZHOU Sheng-zeng.Application of hyper-beamforming in spectrum analysis of passive sonar [J].Technical Acoustics,2010,5(10):460-462.
[4]李启虎.声呐信号处理引论[M].北京:科学技术出版社,2012.
[5]HEIKO S.Passive sonar detection improved by hyperbeam TM technique[C].UDT,2006.
[6]聂良春.超波束(HBF)用于波束锐化[J].声学技术,2008,6(12);892-895.NIE Liang-chun.Hyper beamforming (HBF)technique for beam narrowing[J].Technical Acoustics,2008,6(12):892-895.
