适用于Kappel桨的面元法尾涡模型
2014-12-07王展智
王 睿,熊 鹰,王展智
(海军工程大学 舰船工程系,湖北 武汉430033)
0 引 言
流体力学的相关理论表明,对于近似为有限翼展的单个螺旋桨桨叶而言,存在很明显的翼端效应,它导致了桨叶的径向环量分布发生变化,从而形成尾涡面。面元法计算中的尾涡模型即是基于这样的实际给出的。对于Kappel桨,几何结构如图1所示。图中的Kappel桨选取了台湾海洋大学的Kap5XX 系列桨[1-3]。
由图1 可以看出,Kappel桨在叶梢端弯曲比较剧烈,从几何参数上表述即是Kappel桨叶梢端剖面的纵倾沿径向变化比较明显,具体情况如图2所示。
普通螺旋桨的纵倾线(叶片参考线在图2 平面内的投影)一般如图2 中OAC 段所示,即在AC 段纵倾不剧烈,但Kappel桨从图2 中A 点处开始向叶背一侧弯折,纵倾值沿径向剧烈变化。纵倾变化的不同导致了Kappel桨AB 段的桨叶剖面垂直于纵倾线,而不是垂直于图中的R 轴,否则在叶梢端桨叶厚度将不能保证。

图1 Kappel桨侧视图和正视图Fig.1 The side view and front view of Kappel propeller

图2 叶片参考线变化示意图Fig.2 The diagram of blade reference line
初步分析Kappel桨的几何结构与流场的相互作用可知,梢部弯折能够防止梢部绕流,起到了耗散梢涡的作用,从而增加了桨叶的载荷。基于这样的事实,若用面元法计算Kappel桨时,继续沿用已有的尾涡面,就没有考虑到梢部弯折所造成的梢涡耗散,有可能造成较大的误差。因此有必要对已有的面元法尾涡进行相关的修正,而如何定量描述梢部弯折后所带来的尾涡面的变化,是需要研究的问题。
1 面元法计算的相关说明
在修正尾涡前,先对面元法计算中的有关问题加以说明,以明确本文修正尾涡的思路。面元法是以调和函数的格林公式为数学基础,在桨叶表面和尾涡面上布置奇点来模拟流场经过桨叶时的运动状态。面元法基于势流理论,因此无法模拟流场中涡的形成过程,实际情况下,由于粘性作用,螺旋桨尾流是非势流区(严格来讲,桨叶周围流体也有非势流区),因此运用基于势流理论的面元法求解时需要将这一部分非势流区去掉,已有面元法的处理是将其视为无厚度的势流间断面,在这个间断面的两侧速度势有跳跃,速度势的法向导数连续,以此尾涡面及螺旋桨表面构成了整个面元法的求解边界。其中,尾涡面一般由根据经验和假设构建的尾涡模型表示。对于定常问题,假设尾涡模型上每一半径处的尾涡条带上,偶极子顺着尾涡模型下泄,因此偶极子强度相等,式(1)可以说明这一假设的合理性。


图3 叶剖面环量示意图Fig.3 The circulation of the section
图3 中,A,B 可以是尾涡面上的任意位置,而Γ1和Γ2相等。由此,结合式(1)可知,与每一剖面对应的尾涡条带上,速度势的突跃值相等,均等于绕剖面的环量值。而由尾涡面与螺旋桨的连续性,可以假定尾涡面上偶极子强度值等于对应的桨叶随边处上、下叶面的速度势之差,这也是Morino 库塔条件的由来,Morino 库塔条件如下式:
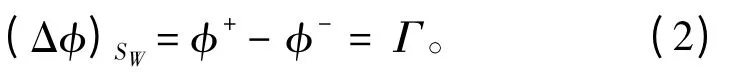
式中:Γ 对应桨叶叶剖面的环量;SW为尾涡面;φ+(-)为对应半径处随边上、下叶面的速度势。显然,对于二维问题,以上假设成立,但在实际流场中,由于积分周线内叶剖面区域外有涡的存在,这样的处理会有误差。
2 弯折三维翼和平直三维翼剖面环量计算与分析
式(2)的重要意义在于它建立了桨叶剖面环量与对应半径处尾涡条带上偶极子强度关系,联系到前面提到的Kappel桨梢部弯折能够起到桨叶加载的作用,可以认为Kappel桨的梢部加载实际上是增大了桨叶剖面处的环量值,因此有必要运用一定手段来模拟弯折后桨叶环量分布的变化情况。本文为了研究问题的方便而又不失模拟的有效性,选择几何尺寸相似的平直三维翼和弯折三维翼进行CFD 模拟,所研究的三维翼剖面参数和展长以及弯折情况都是以Kappel桨单个桨叶为原型的。CFD 计算的过程 中,选 择 0.3R,0.4R,0.5R,0.6R,0.7R,0.8R,0.9R的剖面处环量作为计算的目标,积分周线选取包围剖面的圆周线,理论上积分周线可以是包含桨叶剖面的任意周线,但实际情况中,考虑流场中涡的存在,积分周线最好不要延伸到尾流区,同时,积分周线应避免在叶剖面的边界层内(实际上本文对同一剖面不同半径的积分周线环量进行了计算,结果略有差别)。具体三维翼的几何外形和积分周线的选取如图4和图5所示。
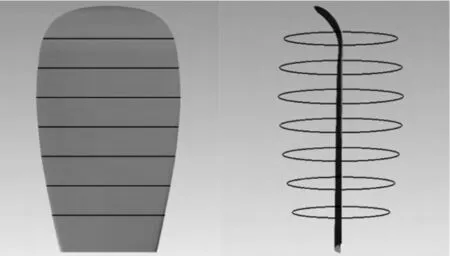
图4 弯折三维翼几何外形和积分圆周线Fig.4 The geometry and circular integral line of curve 3-D foil

图5 平直三维翼几何外形和积分圆周线Fig.5 The geometry and circular integral line of stright 3-D foil
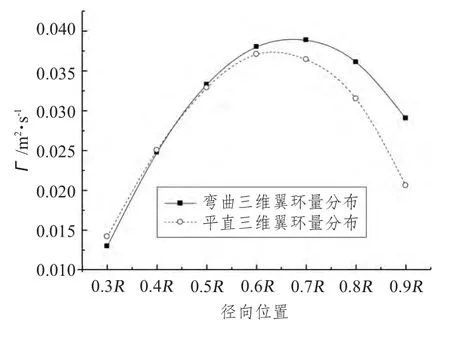
图6 弯折三维翼和平直三维翼环量分布对比表Fig.6 The circulation distribution of curve 3-D foil and straight 3-D foil
CFD 基于粘性流求解,它考虑了流场中涡的存在,面元法仅在桨叶表面布置奇点,但它也等效得到了桨叶周围速度的分布状况。因此,在一定的误差范围内,运用CFD 计算得到各个周线上的速度分布,将其沿周线积分即得到各个剖面的环量分布与面元法求得的环量分布等效,因此可以将其作为面元法计算中的桨叶剖面环量分布。具体计算结果如图6所示,计算过程中来流速度设为2.5 m/s,翼根界面当作对称面。本文对计算得到的剖面环量运用升力公式求得的升力能较好符合CFD 求得的三维翼的升力,从而可以认为环量的结果可信。由图6 可知梢部弯折后的三维翼环量在0.3~0.5 R 之间比平直三维翼环量略小,从0.5 R 左右环量分布开始逐步增大,越靠近梢端环量值增大越多,在0.9 R 处环量增幅最大。因此可以认为弯折的梢端对三维翼加载的范围有限,对于本文所研究的问题可以认为加载范围是从0.5 R 左右到叶梢端,由此对比可以近似认为,Kappel桨的梢端加载范围也是0.5 R 以后。
3 尾涡修正及计算
在大多数情况下,尾涡面模型是经验的模型,在某种程度上,它能够得到较好的计算结果。但这并不能说明它很好的模拟了尾流真实的运动状态。因此在遇到特殊问题时,已有的尾涡模型可能得不到较好的数值计算结果。例如,对于本文所研究的Kappel桨,已有的尾涡模型就无法模拟出叶梢部的加载情况。这就有必要在分析流体与Kappel桨的作用状况后,对已有的尾涡模型进行相关修正,以得到较好的数值计算结果。目前已公开发表的有关面元法分析Kappel桨的文章[2-5]还很少,尤其对细节方面的处理描述不多,对于已有面元法计算分析Kappel桨的效果也没有较明确的说明。对Kappel桨分析时,最初运用已有面元法对台湾海洋大学的Kap5XX 系列桨进行敞水性能计算,所得到的结果与试验值差距较大,于是在前面分析基础上,考虑对面元法计算分析Kappel桨的尾涡进行修正。
修正尾涡模型主要从两方面考虑:1)Kappel桨叶梢端的弯折,导致了叶梢端的加载,从而叶梢部分半径处剖面的环量将增大,叶梢剖面的环量增大后,所对应的尾涡半径处的偶极子强度将增大,若运用以前的尾涡模型将不能很好的体现这一点;2)由于Kappel桨的梢端弯向叶背一侧,梢端的螺距角较小,因此来流在Kappel桨沿叶梢端的径向也有一定的速度,面元法中认为尾涡的走向和流线平行,因此可以认为尾涡收缩的比率比普通螺旋桨要大。
基于以上尾涡模型修正的考虑,一方面应增大尾涡半径的收缩比率,多收缩的径向长度可以近似认为是桨叶叶梢端弯折段的长度。另一方面应增大叶梢附近的尾涡面上偶极子强度,偶极子强度增加值应以CFD 计算得到的三维弯折翼的剖面环量增加值为基础。但在本文中,为了利用已有的尾涡模型,采取了一种等效上述效果的处理办法。本文的Kappel桨桨叶从0.9 R 左右开始剧烈弯折,于是选择将0.9 R 到桨叶叶梢的尾涡条带上偶极子平均叠加到桨叶0.5~0.9 R 半径段的尾涡条带上,而0.9 R 到桨叶叶梢的尾涡条带上偶极子强度将置0,同时,对尾涡收缩到不变的半径值减小0.1 R。将0.9 R 到桨叶叶梢的尾涡条带上偶极子置0,即是将这一部分尾涡去掉,相当于尾涡收缩,而将0.9 R 到桨叶末端的偶极子强度叠加到0.5~0.9 R 段的尾涡条带上,相当于增加这一半径段的剖面环量值。处理办法可用下式表示:

式中:mp为径向划分网格数;Δφi为尾涡面第i个半径处的偶极子强度。对于本文的20 ×20 网格划分,mp-9 近似为0.5 R 左右,符合前文验证的弯折三维翼的剖面加载范围,mp-3 近似为0.9 R 左右。
实际上式(3)是一种等效的处理办法,它是尾涡收缩和梢端环量加载的一种综合作用效果,这样的处理并没有改变尾涡作为势流边界这一原则性问题,只是将边界上值的大小和范围作了改变,而实际上决定尾涡面上的偶极子强度的Morino 库塔条件也只是近似成立。因此从面元法数值求解角度看以上的处理办法合理。
修正尾涡面后,重新对Kap505桨和Kap512桨进行了敞水性能的分析并与未修改尾涡的面元法计算结果以及试验值进行对比。计算过程中选择Kap505和Kap512桨作对比,主要是考虑到它们几何构造的差别相对较大,叶梢剖面最大弯折角度(剖面与纵倾线的夹角)分别为66.04°和88.2°。具体结果如图7和图8所示。图中BEMG 代表修正尾涡面的面元法计算结果,BEM 代表未修改尾涡面的面元法计算结果,EXP 代表试验值。

图7 Kap505 敞水性能计算结果对比图Fig.7 The open water performance comparison of Kap505

图8 Kap512 敞水性能计算结果对比图Fig.8 The open water performance comparison of Kap512
由图7和图8 可看出,修正尾涡面后,面元法的计算结果有很大改善。图7和图8 采用的计算结果均是Morino 库塔条件下得到的结果。这是由于在用此方法进行尾涡修正后,等压库塔条件的数值处理还有待进一步探讨。但目前面元法计算时,大部分采用牛顿迭代法,以Morino 库塔条件求出的奇点强度作为迭代初值,以等压库塔条件作为迭代式,而实际上牛顿迭代法要求初值与真值很接近,因此可以认为Morino 库塔条件结果与等压库塔条件结果差别不大。结合前文对于Morino 库塔条件的说明,认为文中所提出的尾涡修正,能很好的符合Kappel桨敞水性能的计算精度要求。
对于Kappel桨,大部分从0.875 R 左右开始弯折,计算过程中也对从不同径向处(分别是0.8 R,0.9 R,0.93 R)开始弯折的三维翼进行了剖面环量值的计算,结果表明梢端弯折所造成环量增加范围和大小变化不大。另外计算所选的Kap505桨和Kap512桨叶梢端的弯折程度不同,因此,可以初步认为文中所提出的尾涡模型对Kappel桨适用。
4 结 语
本文运用CFD 对几何尺寸相似的弯折三维翼和平直三维翼进行环量分析,得出了梢端弯折后对三维翼剖面环量分布状况的改变。并以此为基础,结合Kappel桨特殊结构对梢端流场的影响,对已有面元法的尾涡模型进行修正,在Morino 库塔条件下得到了与试验值符合较好的计算结果,同时针对Kappel桨的库塔条件进行相关分析,对本文选择Morino 库塔条件下的面元法计算结果作出说明。
[1]JUSTIN E K,SPYROS A K,LEE J T,et al.A surface panel method for the hydrodynamic analysis of ducted propellers[J].Tran.SNAME,1987.
[2]ANDERSEN P,FRIESCH J,KAPPEL J J,et al.Development of a marine propeller with non-planar lifting surfaces[J].Marine Technology,2005,42(3):144-158.
[3]CHENG Hsun-jen,CHIEN Yi-chung,HSIN Ching-yeh,et al.A numerical comparison of end-plate effect propellers and conventional propellers [J].9thInternational Conference on Hydrodynamics,Shanghai,China,2010,10(11~15):495-500.
[4]ANDERSEN P,FRIESCH J,KAPPEL J J.Development and full-scale evaluation of a new marine propeller type[A].97thHauptversammlung der Schiffbautechnischen Gesellschaft,Hamburg,2002.
[5]ANDERSEN P.1997 A comparative study of conventional and tip-fin propeller performance,Proceedings,21stSymposium on Naval Hydrodynamics, June 1996,Trondheim,Norway.Washington,DC,National Academy Press,930-945.
[6]大翼尖倾斜螺桨之设计与空间几何表示[D].基隆:台湾海洋大学,2008.
[7]黄意程.非平面螺桨之效率与空化性能探讨[D].基隆:台湾海洋大学,2008.
[8]锺佩珊.非平面螺桨之效率与空化性能探讨Ⅲ[D].基隆:台湾海洋大学,2010.
