船舶系泊系统动力分析
2014-12-07李继锁朱克强孙培军
李继锁,朱克强,孙培军,王 晨
(宁波大学 海运学院,浙江 宁波315211)
0 引 言
海洋作为战略性的资源基地,其中蕴含着极其丰富的油气资源[1]。然而这些资源的探测、开采和运输都要用到海洋平台以及各类船舶。要使这些海洋结构物安全地生产,必须要有可靠的系泊系统来为它们定位,这就促使系泊动力分析成为一项重要的 技 术 领 域。Childers,Niedzwecki,Casarella 及Nath and Felix[2-7]等对系泊缆索的动力分析做出了重要贡献。
为了逼真地模拟系泊系统的动力特征,必须满足以下要求:
1)建立一个数学模型模拟系统;
2)获得所有环境载荷的计算方法[8];
3)确定并将系泊系统的刚度特点应用到船舶的动力分析之中。
一旦得到缆索恢复力与时间的关系,就可以推导出船舶的运动方程。
通过对船舶运动方程的求解,可以得到缆索的张力特性,这对系泊系统的动力分析非常有意义。
本文讨论船舶在系泊系统作用下的动力特征,采用拉格朗日方程对缆索的动态特性进行计算,得出缆索在动态情况时张力随时间的变化关系。通过船舶的三自由度运动方程比较缆索在准静态和动态时的张力特点,得出船舶的动态特性对缆索张力的影响。
1 缆索数学模型
为了得到一种预测缆索动态特性的方法,Khan和Ansari 把缆索抽象成由多个部分组成的动态系统,然后用运动方程来表示张力与船舶位移之间的关系。缆索的数学模型可由多阶自由变量构成,并且可以把2个节点之间的部分看成是无质量的刚性连接。
以锚的坐标为(x0,y0)建立坐标系,根据拉格朗日方程:
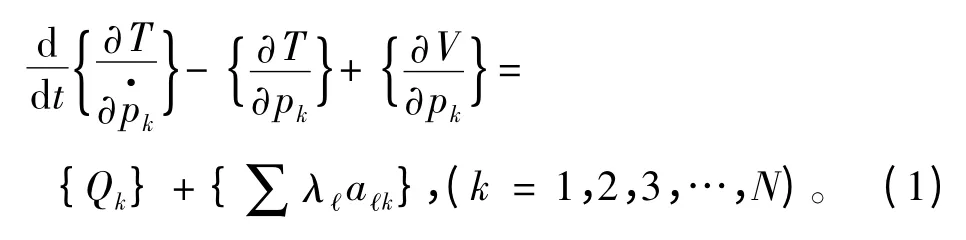
式中:T,V 分别为系统的动能和势能;p1,p2,…,pn为一组用于定义系统运动的坐标;N为坐标个数;λℓ为拉格朗日乘数;Qk为作用在pk上的广义不守恒力;aℓk定义为,(ℓ = 1,2...c;k = 1,2,…,N);fℓ为关于常数c的方程。
对于n 段缆索模型,其动能和势能为:
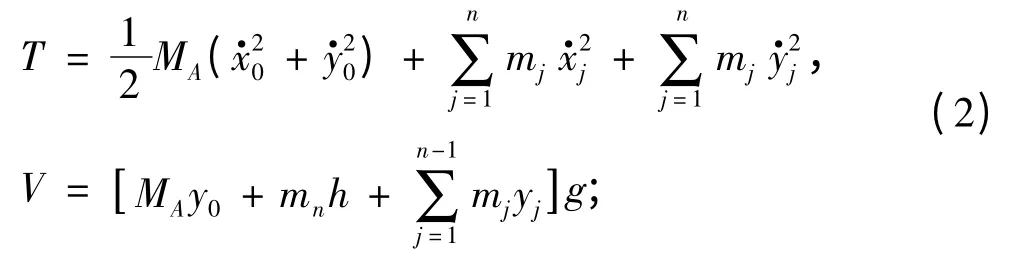
缆索所受的约束为:

锚的运动方程为:

n 段缆索模型也可以用如下n个方程组成的矩阵方程[9]表示:

虚功率和缆索广义力[10]的关系为:

缆索p 段受到的切向和法向力为:


那么可由式(7)得到切向力和法向力。而缆索的切向力相对于其他力非常小,可以忽略不计,则p 节点的广义力为:

缆索的尾端力为:

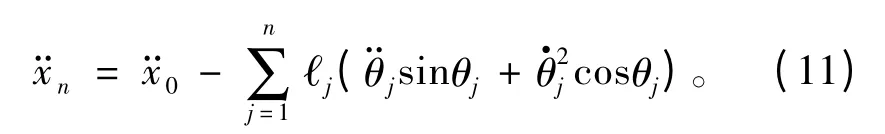
由此可得相邻部分的张力关系为:

根据式(10)~式(12)从第n 段开始计算就可以计算出缆索张力和时间的关系。
2 船舶动力分析
船舶动力分析最准确的方法是使用船舶的六自由度运动方程,但这种方法过程复杂,计算量大,因此一般情况只使用三自由度运动方程进行计算。船舶的运动方程如下:

由于系泊系统的动力特性与任意时刻的船位有关,那么Qx,Qy,Qα可表示为:

式中:βj为第j 段缆索与x 轴的夹角;为缆索的水平张力;为船舶质量中心在坐标原点时船舶导缆孔的初始坐标。
3 数值求解
以上得到的一系列关于缆索的方程均可以表示成如下形式:

式中:M为质量矩阵;{F}为力的列矩阵。
以缆索的静态平衡外形作为初始条件,如果知道任意时刻的θs和,代入[M]和{F}就可以得到关于的方程,并用高斯消元法对方程进行化简得到n个非线性的方程组,然后使用Runge-Kutta[12]计算法求解。
系泊船舶的运动方程是一组二阶、非线性相关的微分方程。文中为简化运算采用了3 自由度数学模型,则有3个方程表示船舶在横荡、纵荡和首摇方向上的运动。在使用Runge-Kutta 计算法之前先确定一个缆索的平衡外形作为Runge-Kutta 计算法的初始条件,接着就可以计算出缆索的水平投影,与此相对应的缆索的张力就可以从张力-位移图[13]中查到。
对于其他时变力和力矩,如波浪力、风力、洋流力等可以根据具体的海况计算得到,然后就可以使用Runge-Kutta法解船舶的运动方程,这是一种自启方法,只要提供初始条件就可以计算出每一步的结果直到所给的时间上限。若所取的计算时间比较合适,那么可以计算出x,y,α,在一个时域内的值,所得的结果比较准确。因此就可以研究任何时刻的系泊系统,并且可以得到缆索张力与船舶横荡、纵荡和首摇运动之间的关系。
4 算例参数
选用工作水深15.2 m的浮式生产船的系泊系统为研究对象,该系泊系统是由6 根多组件缆索组成的多锚腿系统。6 根缆索间隔60°均匀布置,船舶的主尺度为60 m×18.3 m×4.3 m,吃水2.3 m,并且在1.82 m的随机横浪中工作。缆索长152.4 m,直径54 mm,锚抓力为444 kN,在距锚45.7 m 处有一44.4 kN的配重。
5 结 语
1)由准静态分析可知,在船舶横荡以及迎流缆预紧力为89 kN 时,同时由于纵荡和首摇运动作用比较弱,可忽略不计,只有在船舶最大横荡时缆索的配重才离开海底,但此时缆索的张力也只有最大值的30%,这时锚能够提供足够的抓力,维持系统的安全。
2)由动态分析可知,系泊系统在波动后恢复平衡的速度非常快,并且迎流缆在船舶横荡运动时,每个周期的最大张力相差较小,这对研究船舶系泊缆索在随机横浪作用下的特性非常有意义。
3)在考虑缆索动态影响时,可以得到在船舶平均横荡0.55 m 时,迎流缆的平均张力为262 kN。在船舶最大横荡时,迎流缆的张力可达到435 kN,但相比于准静态要小,而迎流缆的平均张力却要比准静态高111%。
4)在考虑缆索的动态影响时,背流面缆索会有更大的张力,而迎流面缆索的张力却相对较小,同时所有缆索的平均张力都比准静态时要大。
[1]ZHANG Huo-ming,YANG Jian-min,XIAO Long-fei.A view on the hybrid model test technique for deep sea platform[J].China Offshore Platform,2004,19(5):1-6.
[2]CHILDERS.Mooring system for hostile waters[J].Petroleum Engineer,1973(5):58-70.
[3]CHILDERS.Deep water mooring-part I,environmental factors control station keeping methods[J].Petroleum Engineer,1974(10):36-58.
[4]CHILDERS.Deep water mooring-part Ⅱ,the ultradeep water spread mooring system[J].Petroleum Engineer,1974(2):108-118.
[5]CHILDERS.Deep water mooring-part Ⅲ,equipment for handling the ultradeep water spread mooring system[J].Petroleum Engineer,1975(5):114-132.
[6]NIEDZWECKI,CASARELLA.On the design of mooring lines for deep water applications[J].ASME Paper,1975:70-75.
[7]NATH,FELIX.Dynamics of single point mooring in deep water[J].Waterways,Harbours & Coastal Eng.Div.,Proc.ASCE,1975:23-40.
[8]朱克强,郑道昌,等.非线性载荷对船中弯矩响应的影响[J],海洋工程,2011,29(4):130-134.ZHU Ke-qiang,ZHENG Dao-chang,et al.Influence of load nonlinearity on bent moment response of amidship[J].Ocean Engineering,2011,29(4):130-134.
[9]朱克强,等.随机波浪下遥控潜水器(ROV)强非线性耦合空间运动与缆索安全性研究[J],海洋工程,2010.28(2):95-99.ZHU Ke-qiang,et al.A study on the strong nonlinear coupling space movement of underwater tethed remotely operated vehicle & sling safety under irregular wares[J].Ocean Engineering,2010,28(9):95-99.
[10]朱克强,黄剑.复合缆索锚泊下的Spar 平台动态响应分析[J].港工技术,2010,47(1):8-10.ZHU Ke-qiang,HUANG Jiang.Dynamic analysis of spar platform moored by multi-component mooring line[J].Port Engineering Technology,2010,47(1):8-10.
[11]朱克强,刘永林.深海垂直吊放缆索系统固有频率和母船临界运动幅值快速计算方法[J].海洋工程,2009,27(2):41-45.ZHU Ke-qiang,LIU Yong-lin.Fast calculation method for the natural frequency & amplitude of surface ship critical motion of deep sea vertically tethered system[J].Ocean Engineering,2009,27(2):41-45.
[12]ZHU Ke-qiang,LIU Yong-lin,WEI Yue,et al.Dynamic response of underwater vertically suspend systems connected to the surface ship[J].Navigation of China,2009(1):21-23.
[12]ZHU Ke-qiang,ZHU Hai-yang,ZHANG Yu-song,et al.A multi-body space-coupled motion simulation for a deep-sea tethered remotely operated vehicle [J].Journal of Hydrodynamics,2008,20(2):210-215.
