验证型实验的数据分析处理方法探讨
2014-12-07刘永华
刘永华
(丽江师范高等专科学校,云南丽江 674100)
验证型实验的数据分析处理方法探讨
刘永华
(丽江师范高等专科学校,云南丽江 674100)
本文以大学物理实验中典型的验证型实验——牛顿第二定律的验证实验为例,讨论了验证型物理实验中的数学处理方法,得出该类实验中,数学处理方法不但要得出所验证的物理规律的数学式,而且更重要的是要通过计算物理量的相关系数确证该数学式所确立的物理规律成立。
验证型实验 数学处理
物理实验中,验证型实验和研究型实验都是非常重要的两类实验。验证型实验是对已建立的物理规律的验证,研究型实验是通过实验得到物理规律,这两类实验虽然实验目的不同,但从数学处理方法上来看,具有相似性,都是通过实验数据分析确证物理规律或得到物理规律,所以对实验数据的分析处理方法是否得当就显得十分重要。下面以一个典型的验证型实验的数据处理为例进行相应探讨,以期望得出相对合理和妥当的实验数据处理方法。
以大学物理实验来说,验证型实验较多,诸如牛顿第二定律的验证、弹性碰撞实验等等都属于此类实验,其中牛顿第二定律的验证实验为该类实验的典型实验。牛顿第二定律的数学表达式是力与加速度的大小关系可以表达成,要验证这个规律,就是给物体加一个大小为F的力,对应产生一个大小为a 的加速度,得到一个测量点,通过改变力,得到n个测量点后,即可通过适当的数学方法验证这个关系的成立。
类似F=ma 这种线性物理规律,其数学模型都可以归结为y=kx+b 的形式。要得到这个线性关系,就是要得出k 和b。通过测量n组x和y的值,即,在X—Y平面中得到n个测量点。若不考虑实验测量的系统误差,则测量误差应当服从高斯分布,反应在X—Y平面中,既是这n个测量点应当均匀地分布在所求表达式y=kx+b两侧,对第i个测量点,误差为,n个测量点导致的总体误差是最小的。若任意给一个直线,则一是测得到的这n个点不再均匀地分布在直线两侧,二是这n个测量点产生的总体误差水平将增大,甚至可以达到无穷大。由此可知,所求直线y=kx+b即是使得n个测量点的总体误差最小的那条直线。总体误差可以写成但由于误差服从高斯分布,导致理论上而而无法通过此求和值衡量总体误差水平。为使其不因为正负抵消而无法衡量总体误差水平,只要使得所有误差均为正再求和即可,故可用残差来衡量总体误差水平,虽然残差不再是总体误差。使得残差Q( k, b)取最小值的k和b,即为所求直线的k和b。此即最小二乘法的数学思想。据最小二乘法处理,所求k和b即是使得Q( k, b)取最小值的k和b,即有解此式,得
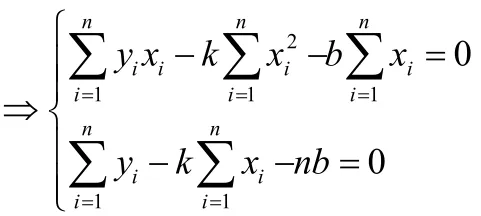
将测量值供稿,即可得到所求k和b。通常大学物理实验中的处理方法,得到k和b,即是验证了y=kx+b[1]。但其实这是不太恰当的。
验证型或者研究型实验,特别是验证型实验,最关键的是需要解决两个问题,一是找出所要验证的关系,第二是要验证得出的关系的确成立,而第二点才是最重要的关键点。即使得出关系y=kx+b,,但如果确证关系不成立,则第一步的工作就变得毫无意义。实际上,任意给出一组,都可以根据最小二乘法得到k和b,即得出y=kx+b,但并不意味着此式的确成立,不能确证物理量k和b的确存在这样的数量关系,并没有检验此物理规律存在。因此,验证型实验做到这一步并不算已经验证被验证的物理规律成立,还需要研究k和b的相关性,通过计算相关系数据r( x, y) 的大小来检验k和b是否的确相关。
总之,验证型实验,是对物理规律的验证,最重要的是确证被验证物理规律成立,得出相应物理量间的数学表达式并不能说已经验证了相应物理规律的成立,最重要的是要通过计算物理量间的相关系数来确证所得物理规律是否成立。
[1]杨述武,赵立竹,沈国土.主编.《普通物理实验1力学、热学部分》.(“十二五普通高等教育本科国家级规划教材)第四版,高等教育出版社,2007年4月,P72.
