使用闪电定位系统测量场估算闪电峰值

巴桑次仁 登增然登 登增扎西

(1.西藏日喀则地区气象局防雷办,西藏日喀则 857000;2.西藏日喀则地区拉孜县气象局,西藏日喀则 858100)

使用闪电定位系统测量场估算闪电峰值

巴桑次仁1登增然登2登增扎西2

(1.西藏日喀则地区气象局防雷办,西藏日喀则 857000;2.西藏日喀则地区拉孜县气象局,西藏日喀则 858100)

雷电的回闪速度具有高多变性的特征,使用遥感测量电或磁场确定一次雷击的闪电电流大小是较困难的,本文中介绍了基于一个假定的回闪模型,运用平均值和标准差统计的方法来估算雷电峰值。分析了传输线(TL)模型与电流远场的关系,并依此来推出回闪电流平均值、电或磁场的平均值、速度的平均值的方程式。分析结果在一定程度上是可以用来估算雷电峰值。

闪电电流 遥感场测量 统计估算

1 摘要

估算闪电回击电流的问题，从应用于测量远距电磁场而广泛使用的雷电定位系统(LLS)已得到更多的关注。由于庞大的数据量，可以通过LLS收集，这样的系统代表一个来源可靠的实验数据是关系到电力和电信系统防雷击保护标准的发展。

测量闪电电磁场来估算闪电峰值电流的方程从文献[1-2]或文献[3]理论中，由关电磁场的闪电电流得到。不过，在从LLS测量电磁场中提取的闪电电流参数还有一个固有的区别，因为如回闪速度这样的未知参数，会因电流接闪的对象，如闪击到一个高大物体，对象不同反射效果不同，影响闪电电流从远距电磁场的推算[5，6]。利用峰值场分布参数法估算峰值电流分布参数的各种方法在[3]中进行讨论。通过分析给出了依据统计估算远距测量的闪电电流理论。

2 从远距电磁场估算闪电电流

2.1 确定性方法

目前涉及远距电磁场表达式和相关回闪基本通道电流，已经被文献[4]给出各种闪电回击模型。这些可以用于估算回闪基本通道电流，和模型中非直接测量参数的估算[4]。附录一根据多种回闪模型总结了远距电场基本通道电流的相关方程式。

可以看出，所有这些方程涉及一定数量的参数，尤其是回闪速度v，在大多数实际情况下是未知的。换句话说，从远距电或磁场来推断其相关的闪电电流，必须假定出回闪速度的值。然而，从一个闪击到另一个闪击的速度变化，统计结果会出现显著变化[5]。由于它遵循从远距场与基本通道电流关系，回闪速度一旦估算错误，会导致几乎估算出相同数量的基本通道错误电流[5]。事实上，远距电场和磁场峰值被确定意味着确定了回闪速度这个参数，从而确定了回闪电流估算峰值。

2.2 统计方法

将定义回闪电流峰值I；回闪速度v；远距电场峰值E作为随机变量，我们假设时空分布的闪电电流沿通道是利用传输线(TL)模型预算[6]。TL模型因其简单性和适应快速多变电磁场峰值的合理性准确性而被采用[6]。然而，我们必须强调，本文中提出这些方法也适用于其它更复杂的回闪模型[6]。

根据TL模型，峰值电流与远距场峰值和回闪速度有关(假设v=const1，地面为良好导体，回闪上升波头没有到达通道的峰值)通过下式表达[6]：

r是闪电通道到观察点的水平距离，c是光速。注意，负号通常不出现在式(1)因为我们需要的只是幅值。如果概率密度函数(PDF)相关的随机变量E和v是已知，，那么有可能获得概率密度函数相关电流I值。大体上，给出随机变量x，y，和z=g(x，y)，这个概率密度函数z可以用x和y表示[6]：

然而，，在许多实际情况下，确切的概率密度函数涉及到的随机变量是未知的。在这些情况下，仍有可能获得估算参数的期望和散布的z，的确，从那些x和y开始，扩展函数g在一系列的点，其中是x和y的均值，平均值和方差的z分别可以被估算见[6]

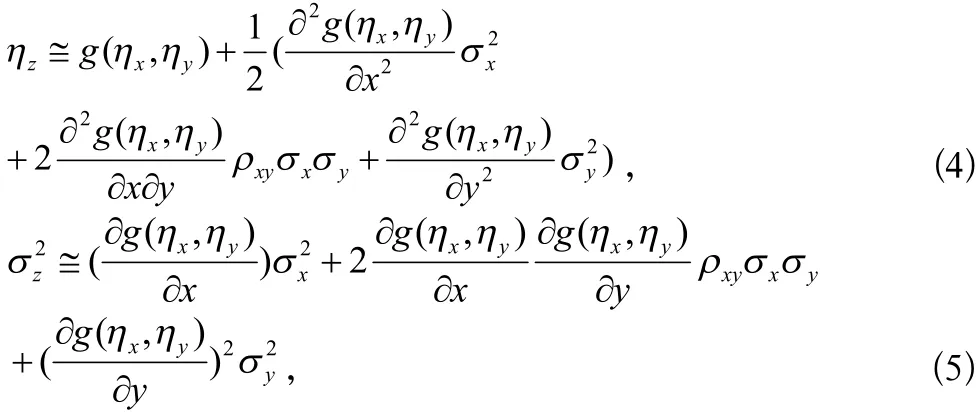
将方程式(4)和(5)代入式(1)，经过简单的数学处理，得出

和

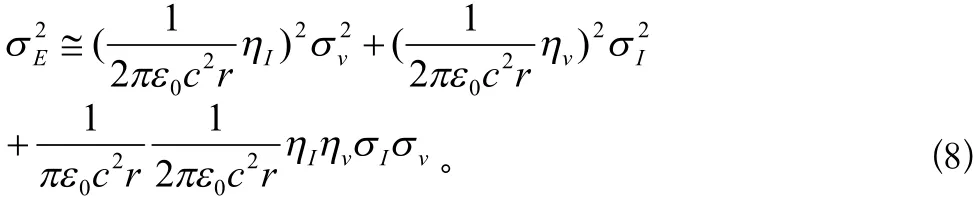
忽略峰值电流和回闪速度之间的任何关联，方程式(7)、(8)分别成为

可以观察到式(9)和式(1)具有相同的数学形式，其中的E、v和I值可以由各自平均值完全取代。这个结果某种程度上对仅使用LLS统计参数从测量场来估算闪电电流的理论以证明。换句话说，虽然从远距测量场估算的回闪速度，没有单次事件的先前经验知识，似乎不可能得到合理准确的回闪电流估算结果，可以用统计法解释，通过LLS场测量获得计算平均值和标准偏差，在不改变所覆盖区域内独立测量，为回闪速度提供可用的统计数据。

3 结语

本文讨论的一个重要问题是从远距电磁场测量估算闪电回闪电流，由于目前日益增长的闪电定位系统利用率，使其得到激增的关注。然而，关键参数的多变性，比如回闪速度，使它在个别事件从远距外测量估算的闪电电流时，不可能获得一个合理精确值。我们在文中表明，统计估算是必要的(例如平均值和标准差)。我们另外介绍的传输线(TL)模型，方程式利用场和速度的平均值来推算回闪电流的平均值，与前者具有相同的函数形式，就像众所周知的TL电流与远距场的关系。这个结果的给出，在某种程度上，验证了LLS一定覆盖区域内回闪速度不多变假设，与使用LLS仅测量场来统计估算闪电电流参数这一理论。

[1]J.C. Willett, J.C. Bailley, V.P. Idone, A. Eybert-Berard, L.Barret, Submicrosecond intercomparison of radiation fields and currents in triggered lightning return strokes based on the transmission-line model, J. Geophys. Res. 94 (1989) 13275-13286.

[2]V.A. Rakov, R. Thottappillil, M.A. Uman, On the empirical formula of Willett et al. relating lightning return stroke peak current and peak electric field, J. Geophys. Res. 97 (1992)11527-11533.

[3]A.O. Lutz, K.M. Mashukov, V.A. Rakov, On estimation of lightning peak current distribution parameters from the distribution of field peaks, TrudyVGI, 72, Gidrometeoizdat, Moscow,1989,pp. 31-35.

[4]F. Rachidi, R. Thottappillil, Determination of lightning currents from far electromagnetic fields,J. Geophys. Res. 98 (1993)18315-18320.

[5]S. Guerrieri, C.A. Nucci, F. Rachidi, M. Rubinstein, On the influence of elevated strike objects on directlymeasured and indirectlyestimated lightning currents, IEEE Trans. Power Delivery13 (1998)1543-1555.

[6]F. Rachidi, W. Janischewskyj, A.M. Hussein, C.A. Nucci, S.Guerrieri, B. Kordi, J.S. Chang, Current and electromagnetic field associated with lightning return strokes to tall towers,IEEE Trans. Electromag. Compatibility43 (2001) 356-367.