软硬互层岩体的加筋作用及敏感性分析

陈 凯，邹 俊

（成都理工大学环境与土木工程学院，成都610051）

0 引言

软硬互层状岩体常见于自然斜坡、工程边坡、隧道工程及采矿工程中，尤以煤系地层中多见，四川盆地广泛分布的红层也多以互层的形式出现。软硬互层状岩体因其强度、弹性模量、泊松比等有分层特征而明显区别于一般的整体状岩体，有着明显的不均匀性和各向异性。软岩中夹有薄层硬岩时，其抗压强度与单纯的软岩相比有明显提高，整体弹性模量也有所增长。薄层硬岩是怎样提高互层岩体强度的，其主要影响因素有哪些？准确把握硬岩的作用及其影响因素，对于分析软硬互层状岩体稳定性和破坏机理有着重要作用。国内外对于软硬互层岩体已有较多研究，D.Quesada等［1］研究了夹层厚度对上下层中裂纹位置及扩展的影响；丁秀丽等［2］研究了软硬互层边坡岩体的蠕变特征，认为软硬互层状岩体蠕变效应显著，导致塑性区向坡内延伸；韩冰等［3］研究了软硬互层岩体的流变特征，认为软岩分层数量、埋置深度及其倾角对复合岩体蠕动变形和塑性区形态均有影响；吉随旺等［4］研究了近水平软硬互层斜坡发生平推式滑坡的机制；胡斌等［5］对软硬互层岩体边坡崩塌的机理进行了研究；宋玉环［6］研究了西南地区软硬互层边坡的变形破坏模式；蒋昱州等［7］对软硬互层岩体卸荷蠕变特征进行了试验研究；夏开宗等［8］对软硬互层边坡稳定性进行了敏感性分析，认为岩层倾角和层间强度对互层边坡稳定性影响较大。目前对软硬互层岩体的研究多从变形破坏模式方面进行研究，或将研究重心放在软岩上，对于互层状岩体中硬岩的作用以及硬岩强度、弹模、软硬岩层厚比、层数、层间结合等对软硬互层岩体强度的影响研究较少。本文拟采用二维颗粒流程序（PFC2D）对几组水平软硬互层状岩石试样进行单轴压缩试验，结合力学分析来研究硬岩在互层状岩体中发挥的作用及其主要影响因素，并对这些影响因素进行敏感性分析。

1 互层状岩体受力分析

1.1 变形分析

软硬互层状岩体具有横向各向同性的性质，因此对各分层进行力学分析是能做到的。兹有软硬互层状岩体承受轴向压应力，软硬岩的弹模和泊松比分别为Es、μs、Eh、μh，其概念模型如图1所示。

对该模型进行力学分析［9－10］，当软硬岩层间结合不良时

从而

式中：σ1为试样所受轴向应力；εs、εh分别为软硬岩的轴向应变；εs′、εh′ 为对应的横向应变。

图1 互层岩体模型

由式（1）可知软硬岩在轴向应力作用下将产生不协调变形。软硬岩在界面处发生相对错动（或有相对错动的趋势），因而该处存在摩擦应力，使软岩在该处承受摩擦应力约束而处于三向应力状态，从而提高其抗压强度。

在层间结合良好的情况下，软硬岩将呈现三向应力状态下的变形特征，软硬岩横向应变分别为：

根据变形协调条件（εs″＝εh″）可解出围压

即互层中软岩的围压由零提高到σ3，而硬岩则受到量值为σ3的拉应力。

1.2 强度分析

由上述分析可知互层状岩体在承受轴向压力时将表现出三向应力状态，由直线型Mohr强度判据［11］可知，岩土体在三向应力状态下的强度条件为

当层间结合不良时，软硬岩的强度分别为：

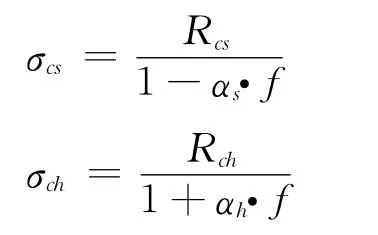
当层间结合良好时，其强度分别为：

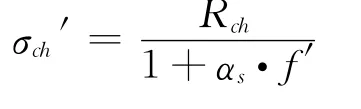
通过上述分析，软硬互层状岩体在单向压缩状态下，软岩和硬岩将出现不一致的变形，使得软岩受到额外的“围压”作用，而硬岩则受到围向拉力作用，从而使软岩强度相对提高，而硬岩强度降低。围向压力和拉力作用在软硬岩界面上，硬岩在互层状岩体中的作用类似于加筋土中土工格栅的作用，本文称之为硬岩“加筋”作用。

根据以上的论述可知，硬岩的“加筋”作用表现为互层岩体强度的提高，这种提高主要依赖于层间结合、形变参数及软硬岩自身强度。但由于“加筋”作用只作用于软硬岩界面上，类似于混凝土压缩试验的环箍效应，其内部作用机制还需借助数值模拟分析。

2 互层状岩体单轴压缩试验数值模拟

2.1 数值模型及试验方案

对近水平软硬互层状岩体进行单轴压缩试验数值模拟，数值模拟在二维颗粒流程序（PFC2D）中进行。试样尺寸采用W×H＝5cm×10cm，首先用四面墙（wall）围成试样外轮廓，各边顶点稍向外延伸，以备试样变形后仍在墙的作用范围内。按试样尺寸在指定范围内生成指定孔隙率和半径分布的颗粒（ball），经一定时步平衡后消除初始应力、位移及浮点、删除侧墙后便制得单轴压缩试验所需的基本试件模型。由于平行黏结（parallelbond model）模型能比较真实地反映真实岩石受力情况［12］，故在本次模拟中采用平行黏结模型。平行黏结力学模型如图2所示，颗粒间的强度为法向黏结强度与切向黏结强度｝决定，而弹模由接触模量kn、ks与黏结模量决定，泊松比由接触刚度比kn／ks与黏结刚度比决定。当黏结破坏后，模型与接触黏结模型（contact bond model）相同，残余强度与颗粒间摩擦系数有关。层间结构面由光滑节理（smoothjoint）模拟，该模型使颗粒间的接触关系垂直于结构面，如图3所示，颗粒可平行层间结构面滑动而避免了“爬坡”效应，从而模拟平直光滑结构面。为研究“加筋”作用对各个因素的敏感程度，将基本模型分成数个组，分别赋予不同的强度、弹模和泊松比及层间结合情况，这些不同条件下互层岩体的强度便可以反映硬岩“加筋”作用的敏感程度。颗粒流数值模型如图4所示，模型共包含颗粒3 219个，颗粒直径为0.5－3～0.75－3m（均匀分布），孔隙率为0.10。

图2 平行黏结模型

图3 光滑节理

图4 颗粒流模型

2.2 加筋作用分析

对软岩和软硬互层岩体进行单轴压缩数值模拟，其应力应变曲线及内部力链如图5所示。其中软岩均采用强度为12.55MPa、弹模为6.3GPa的均质岩石，如图5（a）所示。图5（b）中采用强度为76.2MPa、弹模为38GPa的硬岩，由图可知硬岩的存在使得互层岩体强度提高到26.35MPa，能显著提高互层岩体强度。由图5（a）、5（b）中可以看出，软岩主要发育斜裂纹，而硬岩中裂纹主要为垂直于层面的直裂纹，由此可判断在轴向压缩时软岩主要受剪破坏，而硬岩则主要受拉破坏。由图5（c）可知，在压缩过程中，软岩受剪破坏后内部拉应力几乎全部转移到硬岩上，使硬岩承受较大的拉应力作用，这也是硬岩产生垂直裂纹的原因，在环向受拉时，硬岩为软岩提供了环向约束力，使软岩处于近似的三向应力状态。根据以上分析可知，硬岩在互层岩体中确实起到了“加筋”作用，能有效提高互层岩体强度。

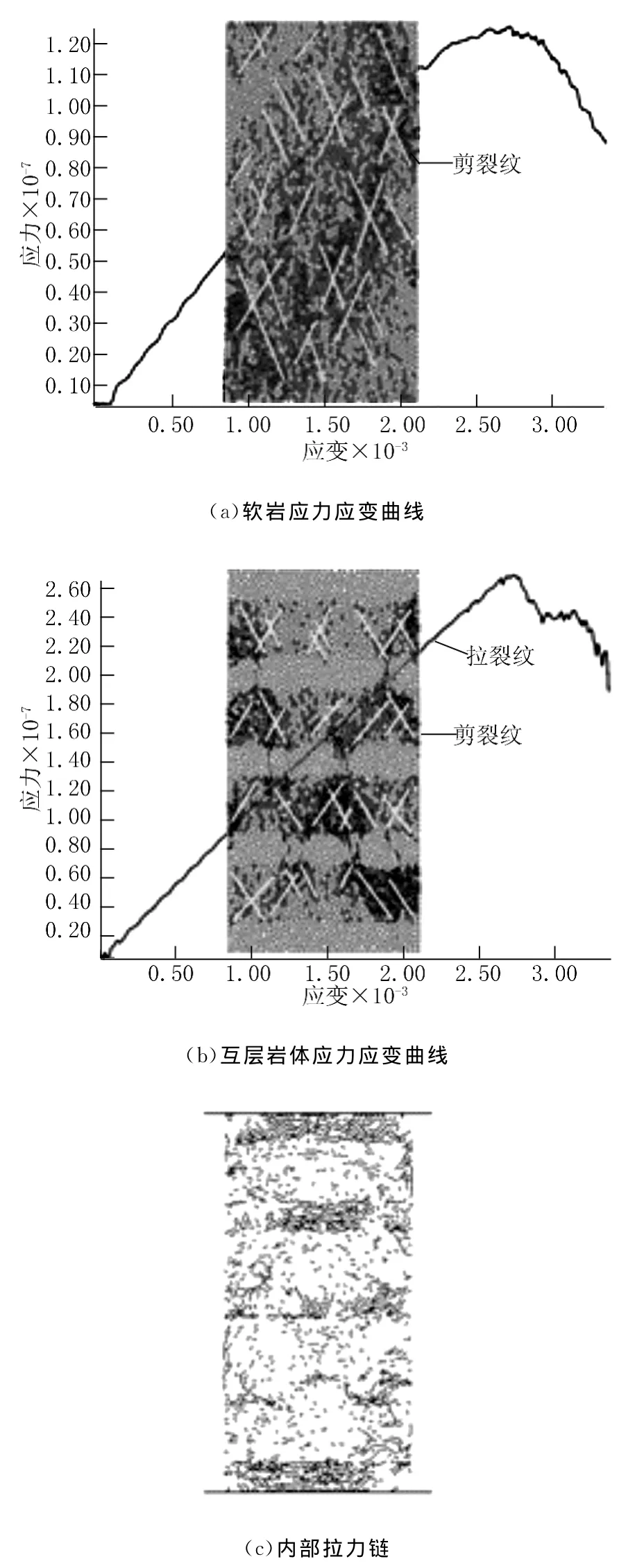
图5 应力应变曲线及力链

2.3 敏感性分析

敏感度是从定量的角度来研究自变量的相对变化引起的因变量的变化率。敏感度可表示为［13］：

式中：ΔAi／ΔA 为因变量的改变率；ΔFi／ΔF 为自变量的改变率，敏感度为正者表明因变量随自变量增大而增大，反之减小。

对于受多种因素影响的因变量，对其进行敏感性分析时可固定其他自变量，单一变化某一自变量来探讨其对因变量的影响。硬岩“加筋”作用的敏感性可表示为某影响因素的改变率与互层岩体强度改变率的关系。

2.3.1 硬岩弹模的敏感性分析

通过第1节受力分析可知，软硬岩层的弹性模量和泊松比的比值决定了软硬岩层的相对变形，因而也决定了两者之间的相互作用。若两者的弹模及泊松比完全相同，则硬岩对软岩不起任何约束作用，只是限制了被硬岩隔开的软岩间裂缝的贯穿。另外，在软岩扩容阶段可能受到硬岩限制作用。一般情况下，硬岩的弹模较软岩大，而泊松比较小，能够很好地限制软岩的变形，进而提高互层岩体的强度。图6是在软硬岩强度不变的条件下互层岩体强度与硬岩弹模的关系，图7是对应的加筋作用对硬岩弹模的敏感度曲线。

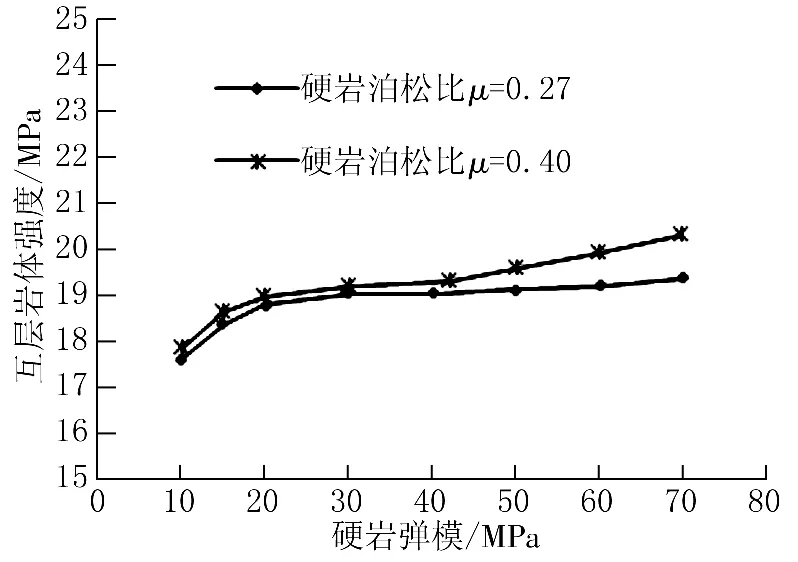
图6 互层岩体强度与硬岩弹模关系曲线

图7 加筋作用对硬岩弹模的敏感度曲线

由图6可知，在保持软硬岩强度不变的条件下，随着硬岩弹性模量的增加，互层岩体强度逐渐增大，在硬岩弹模介于20～40MPa时其强度增长较慢，从图中还可看出，硬岩弹模相同时，泊松比较大者对应互层岩体强度较高，且在硬岩弹模越大时这种提高越明显。从图7可以看出，“加筋”作用对弹模的敏感度较小，总体上呈“V”字形，其最大值小于0.12。

2.3.2 硬岩强度的敏感性分析

硬岩强度是互层岩体强度的重要影响因素之一，它关系到互层岩体在轴向压缩状态下先沿软硬界面滑动还是先将硬岩拉裂或剪断，消除其环向约束作用。图8是在硬岩层厚相同的条件下互层岩体强度与硬岩强度的关系，图9是对应的加筋作用对硬岩强度的敏感度曲线。

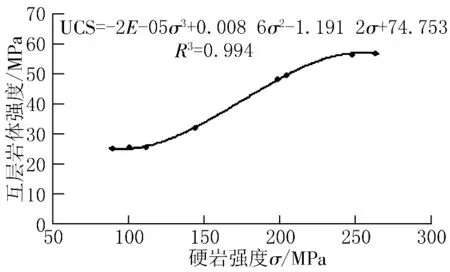
图8 互层岩体强度与硬岩强度关系曲线

图9 加筋作用对硬岩强度的敏感度曲线

从图8可以看出，互层岩体强度在某个范围内随着硬岩强度增长而增加，而在硬岩强度较低或很高时则基本保持稳定。通过观察试样内部力链和宏观破坏时裂缝扩展情况得知，在硬岩强度低时，当内部拉应力增长到某个水平时软岩总是将其拉裂，此时互层岩体强度由软硬岩强度共同控制；当硬岩强度很高时，破坏均为软岩剪切破坏和沿软硬岩界面滑脱，而硬岩保持完整，即这种情况下互层岩体强度由软岩强度及层间结合控制。从图9也可看出，加筋作用在硬岩强度的某个范围内较为敏感，而在两端敏感度均较低，总体上呈倒“V”字形，与其对弹模的敏感度趋势相反。

2.3.3 分层数量的敏感性分析

分层数量在一定程度上影响着互层岩体的强度，分层数量越多，互层岩体越趋均匀，且由硬岩提供的环向约束力总和越大。图10是保持软岩总厚度60mm、硬岩总厚度40mm的条件下互层岩体强度与分层数量的关系。

图10 互层岩体强度与分层数的关系曲线

图11 加筋作用对分层数的敏感度曲线

由图10可以看出，互层岩体强度与分层数成正比，对二者关系进行线性拟合，相关系数达到0.987 7，拟合程度较高，直线截距为12.674 0，与软岩强度相近，符合实际情况。由图11可以看出，加筋作用对分层数的敏感度介于0.2～0.6之间，主要分布于0.5左右。由此可知分层数量越多，加筋作用越显著。

2.3.4 层厚比的敏感性分析

软岩是互层岩体中的薄弱环节，其上下层面均由硬岩约束，根据圣维南原理，当软岩层厚过大时，中部受到端面约束影响很小。此外，当硬岩层厚过小时，在向外挤出的软岩拉应力和硬岩内部剪应力共同作用下易发生破坏。图12是在保持分层总数（7层）不变的条件下互层岩体强度与层厚比（硬岩与软岩分层厚度之比）的关系，图13是对应的加筋作用对层厚比的敏感度曲线。

从图12中可以得知，互层岩体强度随着层厚比的增加而增加。一方面，随着层厚比增加，互层岩体中硬岩所占比例增大，整体岩性更好；另一方面，软岩的层厚相对减小，使其受到约束的厚度占软岩层厚的比例增加，能更好地发挥硬岩的约束作用。根据对互层岩体强度和层厚比关系的拟合可知二者的关系为二次曲线，且在层厚比较小的情况下斜率较大，从图13也可看出当层厚比较小时加筋作用的敏感度较高，随着层厚比的增加，其敏感度逐渐降低，最小值大于0.25。

图12 互层岩体强度与层厚比关系曲线

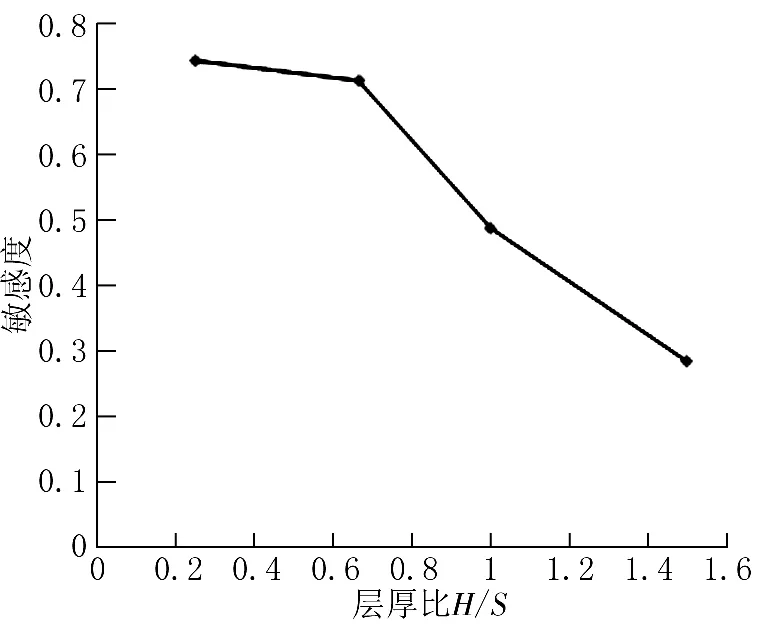
图13 加筋作用对层厚比的敏感度曲线

2.3.5 层间结合的敏感性分析

层间结合情况是互层岩体强度及破坏方式的重要影响指标。当层间结合不良时，由于变形不协调，在软硬岩界面上存在剪应力，承受轴压时硬岩通过层间摩擦来发挥加筋作用，互层岩体易先沿此界面滑动破坏。层间结合良好时，软硬岩界面上无剪应力，硬岩通过层间黏聚力来发挥加筋作用，互层岩体一般破坏方式为压致拉裂和剪切破坏，其强度受软硬岩强度控制，此处仅讨论层间结合不良的情况。图14表示层间结合不良时互层岩体强度与层间摩擦系数f的关系，图15为对应的加筋作用对层间摩擦系数的敏感度曲线。

由图14可知，在层间结合不良的情况下，摩擦系数f小于0.4时互层岩体强度随摩擦系数急剧增加，而当摩擦系数f大于0.4时，互层岩体强度基本保持稳定。从图15中也可看出，加筋作用对摩擦系数的敏感度逐渐降低，当摩擦系数f大于0.4时其敏感度较小。即加筋作用在摩擦系数较小时敏感度较高，而在摩擦系数大时敏感度较低，其敏感度最大值约为0.20。

图14 互层岩体强度与摩擦系数关系曲线

图15 加筋作用对摩擦系数敏感度曲线

3 结论

1）采用二维颗粒流程序（PFC2D）对水平软硬互层岩体进行了单轴压缩数值模拟，结果表明硬岩层能对软岩起到“加筋”作用。加筋作用是通过压缩过程中硬岩为软岩提供环向约束作用而自身承受拉应力来实现的。

2）互层岩体强度随硬岩弹模、泊松比、强度、分层数量、层厚比及层间结合的增加而增加，其中随分层数量和层厚比增加的速率较快，而弹模和层间摩擦对其影响较小。

3）加筋作用对弹模敏感度较小，总体呈“V”字形，其敏感度不大于0.12；在硬岩弹模相同的情况下，加筋作用对泊松比较大者敏感度较大；加筋作用对硬岩强度的敏感度与弹模相反，呈倒“V”的趋势；加筋作用对分层数的敏感度在0.2至0.6之间，有波动；硬岩加筋作用对于层厚比的敏感度有逐渐减小的趋势，最小值大于0.25；对层间摩擦的敏感度逐步降低，其最大值约为0.20。各因素中分层数与层厚比对加筋作用影响最为显著。

4）本文得出的结论是基于一定的软硬岩物理力学参数基础上得出的，对于强度不同的软硬互层岩体，其一般规律可供参考。

［1］Quesada D，Picard D，Putot C，et al.The role of the interbed thickness on the step－over fracture under overburden pressure［J］.International Journal of Rock Mechanics ＆ Mining Sciences，2009，46：281－288.

［2］丁秀丽，付敬，刘建，等.软硬互层边坡岩体的蠕变特性研究及稳定性分析［J］.岩石力学与工程学报，2005，24（19）：3410－3418.

［3］韩冰，王芝银，丁秀丽，等.软硬互层岩体流变特性的数值模拟［J］.长江科学院院报，2007，24（2）：25－29.

［4］吉随旺，张倬元，王凌云，等.近水平软硬互层斜坡变形破坏机制［J］.中国地质灾害与防治学报，2009 （3）：49－52.

［5］胡斌，黄润秋.软硬岩互层边坡崩塌机理及治理对策研究［J］.工程地质学报，2009，17（2）：200－205.

［6］宋玉环.西南地区软硬互层岩质边坡变形破坏模式及稳定性研究［D］.成都：成都理工大学，2011.

［7］蒋昱州，朱杰兵，王瑞红.软硬互层岩体卸荷蠕变力学特性试验研究［J］.岩石力学与工程学报，2012，31（4）：778－784.

［8］夏开宗，陈从新，鲁祖德，等.软硬岩互层边坡稳定性的敏感性因素分析［J］.武汉理工大学学报（交通科学与工程版），2013，37（4）：729－732.

［9］鲜学福，谭学术.层状岩体破坏机理［M］.重庆：重庆大学出版社，1989.

［10］孙训方，方孝淑，关来泰.材料力学 （I）［M］.北京：高等教育出版社，2009.

［11］肖树芳.岩体力学［M］.北京：地质出版社，1987.

［12］Itasca Consulting Group Inc.PFC2Duser's manual［M］.Minnesota：Itasca Consulting Group Inc，2004.

［13］黄高峰，李宗利，牟声远.Hoek－Brown准则参数在边坡工程中的敏感性分析［J］.岩土力学，2009（7）：2163－2167.