A novel trajectory planning strategy for aircraft emergency landing using Gauss pseudospectral method

Shaohua MENG,Jinwu XIANG,Zhangping LUO†,Yiru REN,Nanjian ZHUANG

1.School of Aeronautic Science and Engineering,Beihang University,Beijing 100191,China;

2.College of Mechanical and Vehicle Engineering,Hunan University,Changsha Hunan 410082,China;

3.College of Air Traffic Management,Civil Aviation University of China,Tianjin 300300,China

A novel trajectory planning strategy for aircraft emergency landing using Gauss pseudospectral method

Shaohua MENG1,Jinwu XIANG1,Zhangping LUO1†,Yiru REN2,Nanjian ZHUANG3

1.School of Aeronautic Science and Engineering,Beihang University,Beijing 100191,China;

2.College of Mechanical and Vehicle Engineering,Hunan University,Changsha Hunan 410082,China;

3.College of Air Traffic Management,Civil Aviation University of China,Tianjin 300300,China

To improve the survivability during an emergency situation,an algorithm for aircraft forced landing trajectory planning is proposed.The method integrates damaged aircraft modelling and trajectory planning into an optimal control framework.In order to deal with the complex aircraft flight dynamics,a solving strategy based on Gauss pseudospetral method(GPM)is presented.A 3-DOF nonlinear mass-point model taking into account the wind is developed to approximate the aircraft flight dynamics after loss of thrust.The solution minimizes the forced landing duration,with respect to the constraints that translate the changed dynamics,flight envelope limitation and operational safety requirements.The GPM is used to convert the trajectory planning problem to a nonlinear programming problem(NLP),which is solved by sequential quadratic programming algorithm.Simulation results show that the proposed algorithm can generate the minimum-time forced landing trajectory in event of engine-out with high efficiency and precision.

Aircraft;Forced landing;Trajectory planning;Gauss pseudospectral method;Nonlinear programming

DOI10.1007/s11768-014-3162-7

1 Introduction

With the development of aviation technologies,airplanes are playing an increasing role in transportation.There are millions of passengers travelling by aircraft everyday around the world.Aircraft safety has been a significant concern of researchers and manufacturers.Extensive research has been done to improve aircraft avionics and mechanical systems to reduce the possibility of failures.Nevertheless,the number of accidents is still considerable due to the enormous amount of air traffic flow.

Generally,there are many factors that result in an emergency forced landing,such as mechanic failures,fuel mismanagement,bad weather,bird strike and so on.Once the emergency situations occur,it is crucial for the emergency management system to rapidly select alandingsite,andgenerateafeasibletrajectoryforpilots to safely land the aircraft.Correct postfailure flight plans can prevent a serious failure from evolving into a fatal accident.There are several cases that the pilots safely landed the airplanes after failure occurrences benefited from their rich experience and unmatched skills[1].Unfortunately,it is not replicable for other normal pilots.Therefore,most of the accidents lead to a crash and kill nearly all the passengers.Therefore,trajectory planning becomes one of the fundamental issues of flight safety in emergency situations.

The objective of this research is to develop a strategy to generate a feasible and safe landing trajectory under emergency conditions.The emergency trajectory must address multiple conflicting objectives including minimizing the landing time,meeting safety operational requirements,bounding the degraded flight envelope,and ensuring smooth enough to be tracked.Many approaches have been presented for aircraft trajectory planning,but few of them aim to investigate the forced landing problem,especially in the case resulting from structural damage.Meuleau et al.[2]presented an emergency landing planner for damaged aircraft,in which probabilistic roadmap was constructed by augmenting the edge set of a 2D visibility graph in vertical dimension.Then a hybrid discrete/continuous version of A＊was employed to search for paths of low risk in this roadmap.Atkins et al.[3]described an emergency flight-management architecture applied to trajectory planning for a forced landing in event of loss of thrust.The adaptive flight planner generated the reference trajectory depending on well-defined geometric segments in response to the degraded aircraft performance.Choi et al.[4]extended the traditional Dubins path solver to generate a landing trajectory in cases that aircraft could not maintain straight flight,such as wing damage or actuator failures.Eng[5]designed a 3D Dubins curves planning algorithm,which produced a powerless flight trajectory for unmanned aerial vehicles to a known desired landing site.Adler et al.[6]found a feasible trajectory in three dimensions based on primitive motion elements and graph theory.Three types of basic flight primitives were analyzed:straight flight,gliding flight and turning at a constant rate.Although all the above algorithms perform well,none of them involve the post-failure aircraft dynamics in the trajectory planning process.The flight performance envelope of the damaged aircraft has been changed comparing to the normal one.Therefore the planned trajectories are no guarantee of feasibility for the damaged aircraft.In addition,the algorithms largely ignore the aircraft dynamics,which results in non-optimal trajectories.

Fundamentally,the optimal control theory is most suitable framework to solve trajectory planning problems.It not only takes into account the complex dynamics,but also provides an optimal solution with a given criterion.Much of the literature on aircraft trajectory generation has focused on terrain following and fuel saving[7–9].Brinkman et al.[10]optimized the turn-back flight of aircraft after engine failure.However,rapidly solving optimal control problems for aircraft is still a challenging task[11].Recently,the pseudospectral method has become increasingly popular.Specially,Gauss pseudospectral method(GPM)is considered as a powerful direct computational method for complex nonlinear systems[12].Since the state and control variables are parametrized by a basis of global orthogonal polynomials,the GPM can obtain an improved accuracy with a faster convergent speed.Therefore,the GPM is used to solve the forced landing trajectory planning problem in this paper.

In this paper,the forced landing with loss of thrust is formulated in an optimal control framework that involves the degraded aircraft dynamics and minimizes the landing duration.Then the GPM is selected to convert the trajectory planning problem into a nonlinear programming problem(NLP)which can be solved by sequential quadratic programming(SQP)algorithm.The proposed strategy synthesizes degraded aircraft flight performance characterizing and trajectory planning.Thus the solution is flyable and optimal for the damaged aircraft.

2 Problem formulation

Once there is an emergency situation occurring on board,the pilot or autopilot is required to perform a forced landing immediately.Unlike rotorcrafts,the landingsiteoftheairplaneisextremelylimitedandthecandidate sites include highways,waters and nearby airports.Therefore,the mission of emergency trajectory planning is to safely land the aircraft on a fixed site as fast as possible.The planned trajectory must ensure that all parameters lie within the performance envelope limits of the aircraft,which are determined by aerodynamics,propulsion,and structural characteristics of the aircraft.This section describes the problem as a nonlinear optimal control problem,where the solution minimizes the landing duration subjected to constraints that result from the flight envelope limitations of the aircraft and all the necessary safety and operational requirements.

2.1 Aircraft dynamic model

A generic fixed-wing aircraft model is considered in the current study,as shown in Fig.1.Dynamics of the aircraftaredescribedbydifferentialequationsofapointmass model,which is accurate enough to simulate trajectories.A flat,nonrotating Earth is assumed.The landing flight is considered as fully coordinated flight(no side forces and zero slideslip angle).

Fig.1 Aircraft model in three-dimensional space.

The kinematic equations of the aircraft are given by[13]

where V is the aircraft velocity relative to the wind,γis flight path angle,ψis heading angle,(Wx,Wy,Wz)are components of the wind velocity,and(x,y,z)are the aircraft position in inertial coordinates.

The dynamical equations of the aircraft are given as follows:where m is the aircraft mass;T is the aircraft thrust;g is the gravitational acceleration;α is the angle of attack;μ is the bank angle;and(WV,Wγ,Wψ)are wind components along velocity,heading and flight-path directions.

The aerodynamic forces(drag D and lift L)are defined in terms of dynamic pressure,reference wing area S and dimensionless aerodynamic coefficient CLand CD:

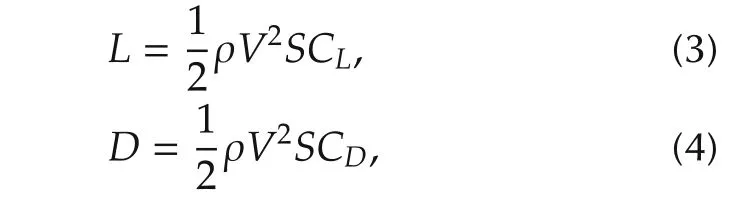
where ρ is the air density that varies with the altitude z,which can be approximated as

Here,ρ0is the air density at the sea level,and zrefis the reference altitude.Lift and drag coefficients CLand CDcan be computed as follows:

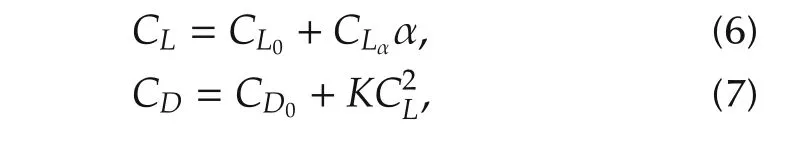
where CL0,CD0and K are constants determined by the aerodynamic properties of the aircraft.

The components of wind speed described along velocity,heading and flight-path directions are given as follows:

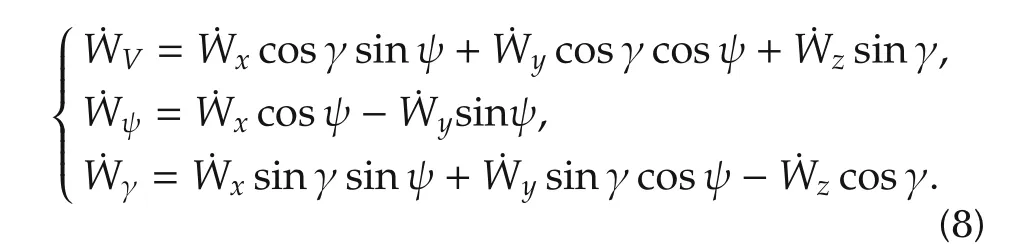
With no loss of generality,it is assumed that only the horizontal wind component Wxis present,which is a function of the aircraft altitude z[14]:

It should be pointed out that the aircraft in reality is controlledbythedeflectionofelevators,rudder,ailerons and throttle.In the case of studying trajectory planning problems,the vehicle is approximated by a point mass,and only the translation motion is considering.The attitude is quickly controlled by the autopilots to maintain the aircraft on moment equilibrium.Therefore,we assume that the aircraft can be directly controlled by the angle of attack and the bank angle.Thus,the state vector is x(t)=[x y z V γψ]T,and the control vector is u(t)=[T α μ]T.

Note that,the presented model is applicable to the nominal aircraft.For the loss of thrust situation,aircraft dynamics are unchanged except that the thrust is zero.Here we ignore the additional drag generated by a shut down engine.Modelling of damaged aircraft for scenarios such as structural damage or actuator failures can be found in[15,16].

2.2 Optimal control problem formulation

When the loss-of-thrust situations occur on board,which can be resulted from engine failure,fuel depletion,or other unforeseen factors,the most important task for the trajectory planner is to guarantee the safety of the passengers.A reasonable option is to land the aircraft at a nearby airport as soon as possible.Therefore,the forced landing is viewed as a minimum-time trajectory planning problem.Furthermore,to successfully track the planned trajectory later,extreme maneuvers are not preferred for the damaged aircraft.There is an additional term in the cost function that considering the operational rates.Therefore,the emergency trajectory planning problem can be described as a constrained optimal control problem.

Determine the state x(t),and the control input u(t),that minimize the cost function

subjecting to the dynamic constraint:

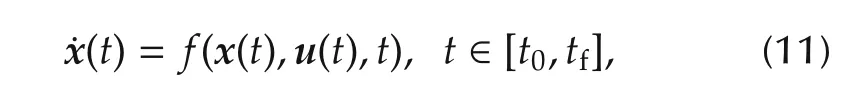
boundary constraints:

20世纪以后，虽然经历了两次世界大战，但法国的成人教育持续发展。1971年颁布的德洛尔法案（LoiDelorsjuillet，1971）是法国成人教育的一个里程碑。该法案将职业教育和成人教育纳入永久教育的范围。该法案规定：接受成人教育是劳动者的权利，所有劳动者都应均等地享有成人教育的机会。其目的是使劳动者适应技术和工作条件的变化，保证他们对经济、文化和社会发展的贡献［3］。

and path constraints:

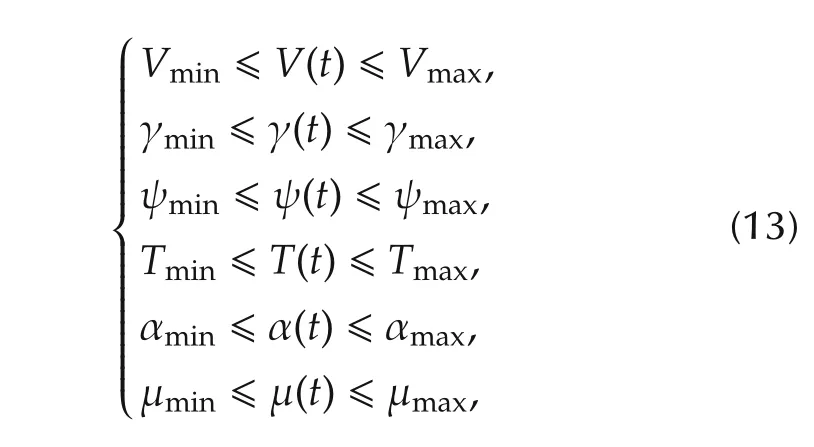
where w1and w2are weight factors,˙α and˙μ are rates of angle of attack and bank angle,respectively.Equation(11)refers to the dynamic equation of the aircraft,equations(12)are the initial and final conditions,and equations(13)denote the state and control constraints,which translate the flight envelope limitations of the aircraft and all necessary safety requirements.

3 Optimal trajectory planning using GPM

3.1 Gauss pseudospectral discretization of trajectory planning problem

The GPM employs a finite basis of global interpolating polynomialstoapproximatethestateandcontrolataset of Legendre-Gauss(LG)points,and then the nonlinear optimal control problem can be converted to nonlinear programming problem,which can be solved by sequential quadratic programming algorithm.The transformation process is shown as follows[17].

Since the trajectory optimization problem is formulated over the time interval[t0,tf],and the LG points lie in the interval[−1,1],the following transformation is performed to express the problem in τ ∈ [−1,1].

Let κ ={τ1,...,τN}be the set of N LG points,and set κ0={τ0,τ1,...,τN,τf}as discretization nodes which include the N LG points,the initial point τ0= −1 and the final point τf=1.Then the aircraft state and control can be approximated by the following polynomials of degree of N+1 and N,respectively.

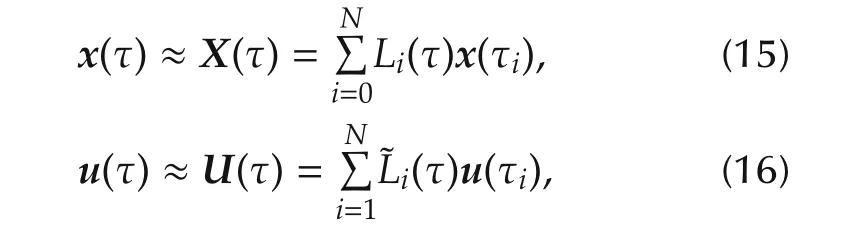
where Liand˜Liare the bases of Lagrange polynomials:

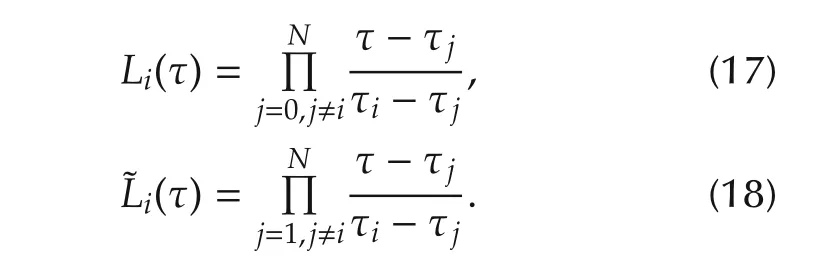
The time derivative of the aircraft state can be approximated as the derivative of the interpolating polynomial.Evaluating the result at the kth collocation point τk,so that

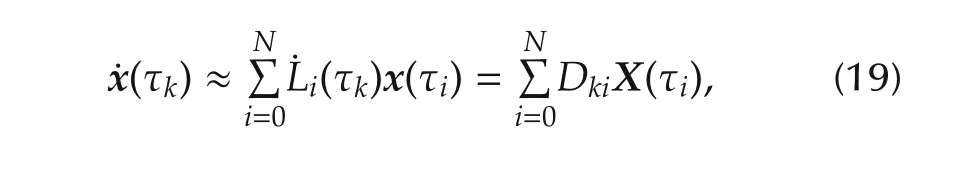
The dynamic constraint(11)is transcribed into algebraic constraints via the differential approximation matrix as

Note that the dynamic constraint is collocated only at the LG points but not at the boundary points.Additional variables in the discretization are defined as follows:x(τ0)=X(−1)and x(τf),where x(τf)is defined in terms of X(τ0),X(τk)and U(τk)via the Gauss quadrature.

Here,ωkare the Gauss weights.

The boundary constraints(12)are expressed at the boundary points as

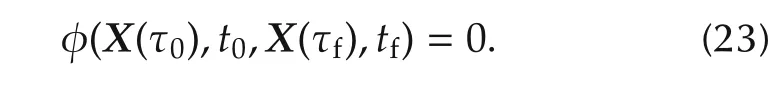
The path constraints(13)are evaluated at the LG points as

Finally,the continuous optimal control problem is converted into a discrete NLP problem,which can be described as follows:

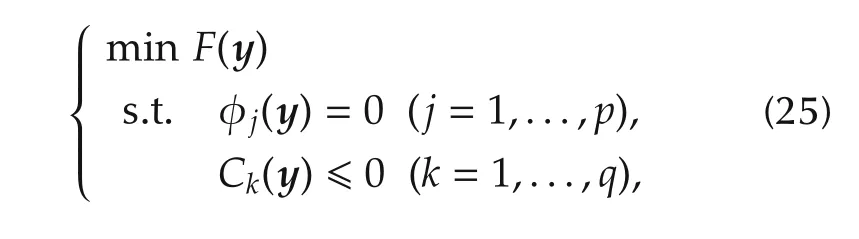
where y is the decision vector consisted of the aircraft state X(τi)(i=0,...,N),control U(τi)(i=1,...,N),and the final time tf.Here,the NLP problem can be solved by the well-developed software packages(e.g.SNOPT[18],IPOPT[19]).

3.2 Computational consideration

The trajectory planning problem has been transformed to a NLP problem using the GPM.Generally,a lot of collocation points are required for a highly accurate solution.However,the dimension of the decision vector dramatically expands with the increase of the collocation points.If the number of LG points is N,then the dimension of the decision vector will be M=9N+1.It would yield a large-scale NLP problem,leading to difficultyofdeterminingtheinitialvalueoftheNLPvariables.Moreover,it is time-consuming to solve a large-scale NLP problem.A reasonable initial guess can lead to a faster convergent speed.In this paper,we propose a multistage iterative optimization strategy:

Step 1 Employ a small number of discretization nodes and an initial guess interpolated between the initial and final conditions to solve the NLP problem,and then obtain a coarse solution.

Step 2 Interpolate the coarse solution with an increasing number of discretization nodes,and then take the result as the new initial guess to solve the NLP problem again.Repeat this step,until finishing the iterations.

According to the above procedure,equations(25)would be solved efficiently.

4 Numerical results

The trajectory planning strategy for forced landing is demonstrated for a generic transport aircraft.Example taken from[20]is recomputed.The model is DC9-30 commercial aircraft,whose parameters are shown in Table 1.Considering the flight envelope limitations of the aircraft and all the necessary safety and operation requirements,the following constraints of the state and control variables need to be satisfied during the whole path.

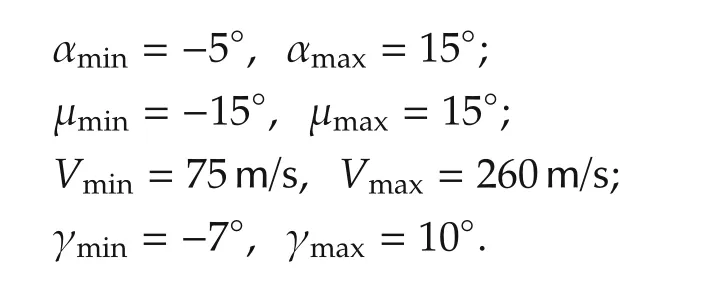
It is well known that an initial guess is essential to NLP solvers because the iteration process is heavily dependent on the initial guess.A bad initial guess may result in inaccurate solution,or even no convergent solution.Therefore it is important to provide a reasonable initial guess for civil aircraft trajectory optimization.As stat-ed in[20],civil aircraft usually cruises at an altitude of about 10km,where the air density is only about 30%of the value at the sea level.Dramatically changing air density during the landing process makes the solution difficult to converge.In this paper,the solution of the landing problem with constant air density is used as an initial guess for solving the real air density problem.

Table 1 Parameters of generic transport aircraft.

The landing maneuver is treated as a minimum-time optimalcontrolproblemwithfixedboundaryconditions.Inthisstudy,theaircraftstartslandingflightatanaltitude z=10km,cruise speed V=240m/s,and flight path angle γ=0°,and need to land a nearby airport using only the angle of attack α and the bank angle μ as control inputs.The positions of the airport is at(120,−30,0)km,with the runway direction ψ=30°.The initial and final conditions for states and controls can be found in Table 2.During the landing flight,the altitude of the aircraft cannot be minus,hence additional constraint is imposed on the state variable z≥0.Here we ignore the size of the aircraft,which is very small comparing with the descending altitude.

In this simulation,we perform two iterations for optimization,in which,the numbers of discretization nodes are Nstep1=8 and Nstep2=40,respectively.The results are presented in Figs.2–10.

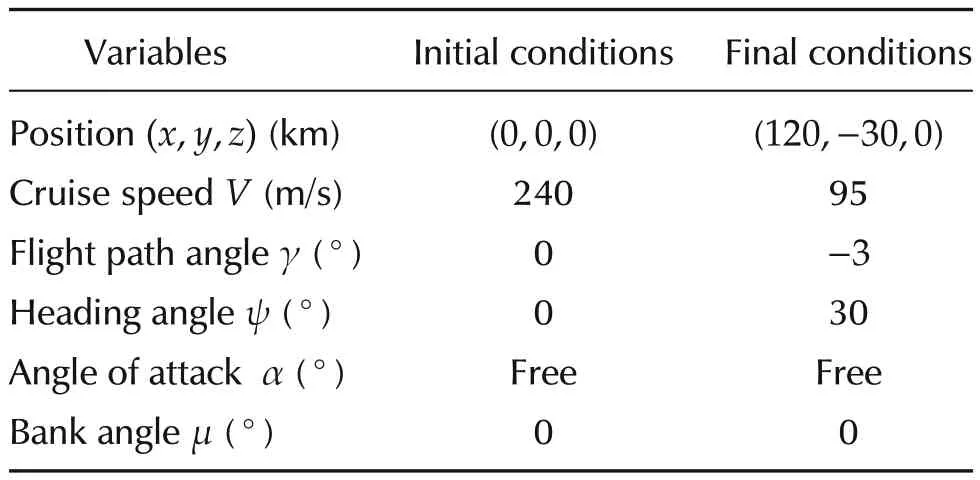
Table 2 Boundary conditions for states and controls.

Fig.2showsthelandingtrajectorywithnominalthrust in three dimensional space.Fig.3–4 are the projections of the trajectories with and without thrust in horizontal and vertical planes.It can be seen that the trajectory profilesarealmostidenticalinbothcases.Thewholetrajectories of the landing flight can be divided into three phases.In the first phase,the aircraft turns slightly right and increases the airspeed to travel along the path as fast as possible.In the meantime,the thrust gradually decreases to zero in the 100%thrust scenario and the flight path angle and heading angle also decrease.In the second phase,the aircraft performs a stable descent in a minus angle of attack with a high airspeed,which can reach the upper boundary in present of thrust.The angle of attack gradually decreases all along the first two phases.In the final phase,the aircraft basically makes a level turn flight to get aligned with the runway and decreases its airspeed to the desired value before touchdown,which should occur gently in a plus angle of attack.Fig.10 shows that it does not use too much thrust to keep the airspeed in the second phase.The minimum timeofthelandingflightis534.5s,whichissmallerthan the gliding time 548.5s.The total runtime of the simulation is about 15s,which is much less than the flight time.Therefore,it can be viewed as fast for realtime implementation.

Fig.2 3D minimum time landing trajectory with thrust.

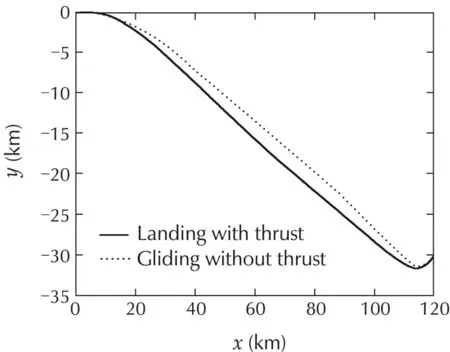
Fig.3 Horizontal trajectory profile.

Fig.4 Vertical trajectory profile.

Fig.5 Airspeed profile.

Fig.6 Flight path angle profile.

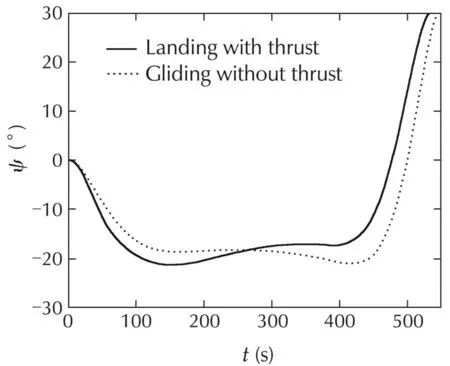
Fig.7 Heading angle profile.

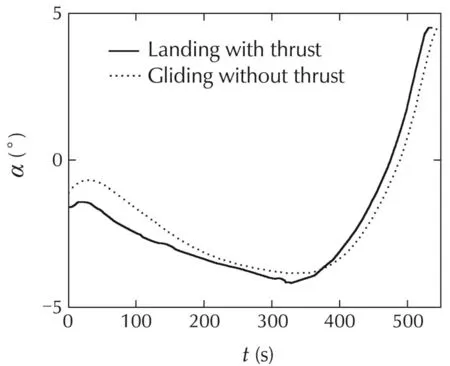
Fig.8 Angle of attack profile.

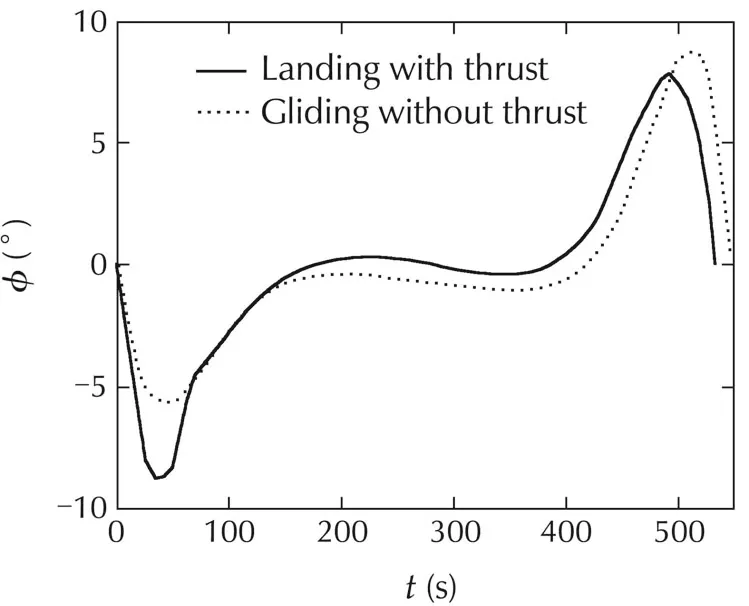
Fig.9 Bank angle profile.

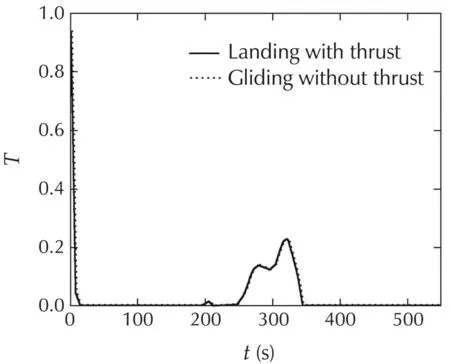
Fig.10 Thrust profile.

5 Conclusions

Trajectoryplanningforagenerictransportaircraftduring the emergency situation of loss of thrust has been studied in this paper.Finding the minimum-time forced landing trajectory was stated as a nonlinear optimal control problem,which was transformed to a NLP problem using Gauss pseudospetral method and then solved by sequential quadratic programming algorithm.The results show that the planned 3D trajectories not only satisfy the damaged aircraft dynamics,path and boundary constraints successfully,but also are smooth and feasible.In addition,the GPM exhibits excellent features of a high convergence speed and solution precision,and is potential to be used for real-time trajectory generation.

[1]R.Watts,P.Tsiotras,E.Johnson.Pilot feedback for an automated planning aid system in the cockpit.Proceedings of Digital Avionics Systems Conference.Orlando:IEEE,2009:1187–1199.

[2]N.Meuleau,C.Plaunt,D.E.Smith,et al.An emergency landing planner for damaged aircraft.Proceedings of the 21st Innovative Applications of Artificial Intelligence Conference.Menlo Park:AAAI,2009:114–121.

[3]M.E.Atkins,A.I.Portillo,J.M.Strube.Emergency flight planning applied to total loss of thrust.Journal of Aircraft,2006,43(4):1205–1216.

[4]H.J.Choi,E.M.Atkins.An analytic trajectory planner for aircraft with sever damage or failures.AIAA Infotech@Aerospace Conference and Exhibit and AIAA Unmanned–Unlimited Conference and Exhibi.Seattle:AIAA,2009:2009–2018.

[5]P.C.Eng.Path Planning,Guidance and Control for a UAV Forced Landing.Brisbane:Queensland University of Technology,2011.

[6]A.Adler,A.Bar-Gill,N.Shimkin.Optimal flight paths for engineout emergency landing.Proceedings of the Chinese Control and Decision Conference.Taiyuan:IEEE,2012:2908–2915.

[7]P.Williams.Aircraft trajectory planning for terrain following incorporating actuator constraints.Journal of Aircraft,2005,42(5):1358–1362.

[8]Y.Zhao,P.Tsiotras.Analysis of energy-optimal aircraft landing operationtrajectory.JournalofGuidance,Control,andDynamics,2013,36(3):833–845.

[9]M.Houacine,S.Khardi.Gauss pseudospectral method for less noise and fuel consumption from aircraft operations.Journal of Aircraft,2010,47(6):2152–2159.

[10]K.Brinkman,H.G.Visser.Optimal turn-back manoeuvre after engine failure in a single-engine aircraft during climb-out.Journal of Aerospace Engineering,2007,221(1):17–27.

[11]J.Betts.Survey of numerical methods for trajectory optimization.Journal of Guidance,Control,and Dynamics,1998,21(2):193–207.

[12]G.Huntington,V.A.Rao.Optimal reconfiguration of spacecraft formations using the Guass pseudospectral method.Journal of Guidance,Control,and Dynamics,2008,31(3):689–698.

[13]Z.Fang,W.Chen,S.Zhang.Flight Dynamics of Aerial Vehicles.Beijing:Beihang University Press,2005.

[14]Y.Zhao.Optimal patterns of glider dynamic soaring.Optimal Control Applications and Methods,2004,25(2):67–89.

[15]F.Fahroo,D.Doman.A direct method for approach and landing trajectory reshaping with failure effect estimation.AIAA Guidance,Navigation,andControlConference.Providence:AIAA,2004:200–209.

[16]Y.Li,L.Yang,G.Shen.Safe trajectory optimization with control failure effects estimation.Journal of Beijing University Aeronautic and Astronautics,2012,38(12):1601–1605.

[17]D.A.Benson,G.T.Huntington,T.P.Thorvaldsen,et al.Direct trajectory optimization and costate estimation via an orthogonal collocation method.Journal of Guidance,Control,and Dynamics,2006,29(6):1435–1440.

[18]P.E.Gill,W.Murray,M.A.Saunders.SNOPT:an SQP algorithm for large-scale constrained optimization.SIAM Review,2005,47(1):99–131.

[19]L.T.Biegler,V.M.Zavala.Large-scale nonlinear programming using IPOPT:an integrating framework for enterprise-wide dynamicoptimization.Computers&ChemicalEngineering,2009,33(3):575–582.

[20]E.Bakolas,Y.Zhao,P.Tsiotras.Initialguessgenerationforaircraft landing trajectory optimization.AIAA Guidance,Navigation and Control Conference.Portland:AIAA,2011:2011–6689.

16 October 2013;revised 9 August 2014;accepted 25 August 2014

†Corresponding author.

E-mail:luozp@buaa.edu.cn.Tel.:+86-10-82338786;fax:+86-10-82338786.

This work was supported by the National Key Basic Research Program of China(973 Program)(No.2011CB707002).

©2014 South China University of Technology,Academy of Mathematics and Systems Science,CAS,and Springer-Verlag Berlin Heidelberg

Shaohua MENG is a Ph.D.candidate at School of Aeronautic Science and Engineering,Beihang University,China.He received his B.E.degree from Beihang University in 2008.From 2012 to 2013,He was a visiting student in Politecnico di Milano,Italy.His researchinterestsincludeaircraftdynamics,trajectory optimization and aviation safety.E-mail:msh1206@ase.buaa.edu.cn.

Jinwu XIANG received his B.E.and Ph.D.degrees from Nanjing University of Aeronautics and Astronautics in 1980 and 1993,respectively.He is currently a professor at School of Aeronautic Science and Engineering,Beihang University.His area of research includes aircraft flight mechanics,structural dynamics and aeroelasticity.E-mail:xiangjw@buaa.edu.cn.

Zhangping LUO received his B.E.and Ph.D.degrees from Beihang University in 1991 and 2004,respectively.He is currently an associate professor at School of Aeronautic Science and Engineering,Beihang University.His research interests include structural dynamics,crashworthiness,aircraft trajectory optimization and aviation safety.E-mail:luozp@buaa.edu.cn.

Yiru REN received his B.E.degree from Harbin Engineering University in 2006 and his Ph.D.degree from Beihang University in 2011.Currently,heisalectureratCollegeof MechanicalandVehicleEngineering,Hunan University,Changsha.His main research interests are crashworthiness and impact dynamics,structural dynamics,structural and multidisciplinary optimization.E-mail:renyiru@buaa.edu.cn.

Nanjian ZHUANG received his B.E.and Ph.D.degrees from Beihang University in 2008 and 2014,respectively.He is currently a lecturer at College of Air Traffic Management,Civil Aviation University of China,Tianjing.His research interests include aircraft flight mechanics and aviation safety.E-mail:znj@ase.buaa.edu.cn.