Robust sliding mode control of general time-varying delay stochastic systems with structural uncertainties

Sheng-Guo WANG,Libin BAI,Mingzhi CHEN

1.Department of Engineering Technology and Department of Software and Information Systems(Graduate Faculty),University of North Carolina at Charlotte(UNC Charlotte),NC 28223-0001,U.S.A.

2.Department of Software and Information Systems,UNC Charlotte,NC 28223-0001,U.S.A.

3.College of Mathematics and Computer Science,Fuzhou University,Fuzhou Fujian 350108,China

Robust sliding mode control of general time-varying delay stochastic systems with structural uncertainties

Sheng-Guo WANG1†,Libin BAI2,Mingzhi CHEN3

1.Department of Engineering Technology and Department of Software and Information Systems(Graduate Faculty),University of North Carolina at Charlotte(UNC Charlotte),NC 28223-0001,U.S.A.

2.Department of Software and Information Systems,UNC Charlotte,NC 28223-0001,U.S.A.

3.College of Mathematics and Computer Science,Fuzhou University,Fuzhou Fujian 350108,China

This paper presents a new robust sliding mode control(SMC)method with well-developed theoretical proof for general uncertain time-varying delay stochastic systems with structural uncertainties and the Brownian noise(Wiener process).The key features of the proposed method are to apply singular value decomposition(SVD)to all structural uncertainties and to introduce adjustable parameters for control design along with the SMC method.It leads to a less-conservative condition for robust stability and a new robust controller for the general uncertain stochastic systems via linear matrix inequality(LMI)forms.The system states are able to reach the SMC switching surface as guaranteed in probability 1.Furthermore,it is theoretically proved that the proposed method with the SVD and adjustable parameters is less conservatism than the method without the SVD.The paper is mainly to provide all strict theoretical proofs for the method and results.

Robust control;Time-varying delay systems;Stochastic systems;Lyapunov methods;Sliding mode control;Time-varying systems

DOI10.1007/s11768-014-4055-5

1 Introduction

Time-delay systems broadly exist in a lot of practical processes and remote systems as well as their networks and control systems[1–10],e.g.,remote control systems[1],unmanned aircraft[3],industrial control systems[4–6],multivariable systems with time-delay[7],Markovian jump time-delay systems[8],and networked control systems[9].Among that,[10]discussed special issues on time-delay systems,and[1]systematicallyaddressed application of time-delay systems in 2007.Because all dynamic systems usually have uncertainties in face of changing environment and disturbances,therefore the research on robust control of time-delay systemshasbeenahotresearchareafordecades[7–10].

Furthermore,many practical systems are stochastic process,especially on circuits,networks,and remote systems,where both variables and processes randomly and dynamically change with the time,including stochastic noises(white and/or colour).Thus,robust controlonstochasticprocesshasbecomeanactiveresearch area,e.g.,using Kalman filtering for stochastic systems with consecutive packet losses and measurement time delays[11],output feedback for stochastic time-delay nonlinear systems[12],a robust stochastic control for hypersonicaircraft[13],robustcontrolofuncertainnonlinear systems with state delays[14],and robust stochastic stabilization with H∞control in the stochastic neutral time-delay systems[15].Recently,Shi,Luan and Liu discussed stochastic incomplete measurement and mixed random delays for discrete-time systems filtering problem[16].

To deal with uncertainties and nonlinearity,sliding mode control(SMC)[17]has been frequently used in uncertain systems[18–23].In SMC,the system structure switches based on the system state vector in order to force the system trajectory toward and/or to stay in a predefined subspace.Because of its excellent performance in face of external disturbances and parametric deviations,the SMC[17]has been widely adopted in many areas,especially in robust control of uncertain systems and electric drives,e.g.,robust stabilization by SMC for uncertain linear input-delay systems with nonlinear parametric perturbations[18],robust SMC for time-delay systems with mismatched structural uncertainties[19],and PD sliding mode observer for fault-tolerant control[20].Furthermore,Niu et al.[21]well proposed a very general uncertain stochastic system model with time-varying delay and used SMC to ensure the robust stochastic stability via LMI approach.In[22],an LMI approach was developed to guaranteed cost control of linear time-delay systems.Also,a delaydependent robust H∞control of uncertain linear state delayed systems was discussed in[23].Recently,Wu et al.studied dissipativity-based SMC of continuoustime switched/jumped stochastic systems[24].All these show the SMC as a heat research area.The research progresshasbeenmadeforrobuststochastictime-delay systems control via the SMC in the literature[1–24].

However,all above-mentioned results on the robustly stochastic stability are sufficient conditions.Some complex systems may not satisfy those sufficient conditions for robustly stochastically stability.Therefore,how to further reduce the conservatism is still a challenging problem,especially for general popular models in view of their practice.

This paper is to address this problem.The main contributions of this paper include

1)proposingless-conservativemethodforgeneraluncertain stochastic systems with time-varying delay and structural uncertainties by introducing the SVD on the structural matrices of uncertainties for uncertain timedelay systems as a first time in the literature;

2)deriving new robust stochastic stability condition for uncertain stochastic time-varying delay systems;and

3)developing and showing the less conservative robust control via the SMC for uncertain stochastic timevarying delay systems based on the above new features.

It is noticed that the structural uncertainties can be defined more physically and naturally as ΔA(t)=where|ai(t)|≤ 1,matrices Airepresent the structural characteristics,and time-varying parameters ai(t)represent their corresponding uncertain variations.It is usually more practical and easier to describe the structural uncertainties in this form than the EF(t)H form[21–24,28],although those two kinds of descriptions may have some relationship.However,the former is much flexible and practical.In the proposed method,we firstly apply singular value decomposition(SVD)to convert the structural uncertainties matrices,and introduce flexible adjustable parameters as Wang and Shieh did for the uncertain systems without Brownian motion(e.g.,[26]).

The partial results of this paper were presented recently at the IEEE CDC 2012[29],i.e.,Theorems 1 and 2 without any theoretical proofs in[29].However,here we have significantly extended the materials by:i)presenting strict theoretical proofs for all theorems in[29];ii)rewriting the introduction and adding more references;iii)adding a new theorem for comparison of uncertaintystructuretreatmentswithandwithouttheSVD;and iv)adding new simulation for different stochastic seeds;as well as v)adding new remarks and removing the simulation and comparison which have been presented in[29];i.e.,just adding new important parts and shorting some existed parts to[29].These make this paper solid and easy to be gripped and applicable to the control systems area and related areas for various readers.

Therestofthepaperisorganizedasfollows.Section2 provides the problem formulation.The main Section 3 presents the SVD method for system structural uncertaintiesinSection3.1,theslidingmodecontrollerdesign in Section 3.2,the robust stability in Section 3.3,and the switching surface reachability analysis in Section 3.4.A new theorem of the general comparison is presented in Section 4.The example with new stochastic seeds is in Section 5.Finally,Section 6 concludes the paper.

2 Problem formulation

In this section,we present the problem formulation of general uncertain stochastic systems that we are treating.It is a kind of general stochastic systems with timevarying delay and structural uncertainties established on the probability space(Ω,F,P)as described in[21]with the Itˆo form as

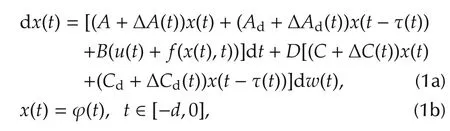
where x(t)∈Rnis the system state vector;u(t)∈Rmis the control input;w(t)is a one-dimensional Brownian motion with E{dw(t)}=0 and E{[dw(t)]2}=dt;matrices A ∈ Rn×n,Ad∈ Rn×n,C ∈ Rm×n,Cd∈ Rm×nand D ∈ Rn×mareknownconstantmatrices;matrixBisafull column rank matrix;matrices ΔA(t) ∈ Rn×n,ΔAd(t) ∈Rn×n,ΔC(t) ∈ Rm×nand ΔCd(t) ∈ Rm×nare unknown time-varying uncertain matrices;f(x(t),t)∈Rmrepresents unknown state-dependent uncertain nonlinear function vector;and τ(t)is the time-varying delay.

Without loss of generality,the following three assumptions hold for system(1):

The above-mentioned structural uncertainties of system(1)are represented in practical and flexible forms as follows:

where Ai,Adj,Ch,and Cdsare constant matrices representing the uncertainty structures;ai(t),ad,s(t),ch(t)and cd,s(t)are time-varying uncertain parameters.Without lossofgenerality,theabsolutevaluesofthetime-varying uncertain parameters are bounded by 1.

The goal is to design a controller with SMC to robustly stabilize the uncertain time-delay stochastic system(1).The stability of stochastic systems is defined below,where Definition 1 can be found in[30],but we modify it by ‖x(t)‖to replace|x(t)|.Operator‖·‖denotes ‖·‖2.

De fi nition 1 The nominal system of the uncertain system(1)with u(t)=0 is said to be mean-square stable ifforanyε＞ 0thereisaδ(ε)＞ 0suchthatE[‖x(t)‖2]＜ ε for all t＞0 whenE[‖ϕ(t)‖] ＜ δ(ε).If,in addition,=0 for all initial conditions,then the nominal time-delay stochastic system is said to be mean-square asymptotically stable.

De fi nition 2 The uncertain stochastic system in(1)is said to be robustly stochastically stable if the system is mean-square asymptotically stable for all admissible uncertainties.

Two Lemmas are used in the proof of main results.

Lemma 1[31] Given a symmetric matrix T=where its sub-matrices have respective appropriate dimensions,andthen the following two properties are equivalent:

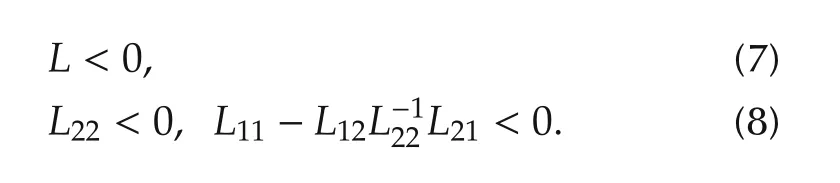
Lemma 2[17] Let P1and P2be matrices with approximate dimensions,and P3be a symmetric matrix satisfying(ε I− P3) ＞ 0 and ε＞ 0.Then,the following inequality exists:

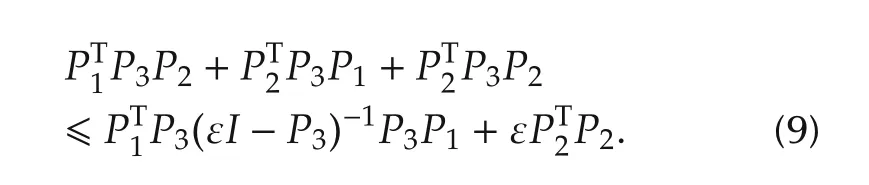
3 Stability analysis for uncertain stochastic systems

This section presents new less-conservative control methods for system(1).

3.1 Eff i cient structural uncertainties decomposition

We apply the SVD method to the structural uncertainties in(3)–(6)as in[32].Then,it leads to

where

Remark 1 The uncertainty treatment in(10)–(13)is more flexible and less conservative than the normal treatment.

3.2 Sliding mode controller design

As the first step of the SMC design,its switching surface function is defined as the following form for timedelay systems:

where s(t)=[s1(t)···sm(t)]T∈ Rm;x(t)is the system state vector;G is chosen to make GB as non-singular as specified in(15)below;and K is the control feedback matrix to be determined.

The following stochastic integral equation is derived

by substituting dx(t)in(1a)into(14)

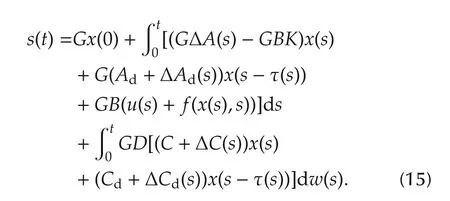
The Brownian motion part of(15)can be eliminated by choosing GD=BTXD=0.Then,we have

MatrixG ischosentobethefollowingformtoguarantee the non-singularity of GB as

Once the system state vector reaches to the switching surface s(t)=0,the system will enter the sliding mode with˙s(t)=0.Hence,by calculating u(t)from˙s(t)=0.the equivalent control law ueq(t)is

Substituting u(t)in system(1)by ueq(t)in(18),we have the system dynamic equation

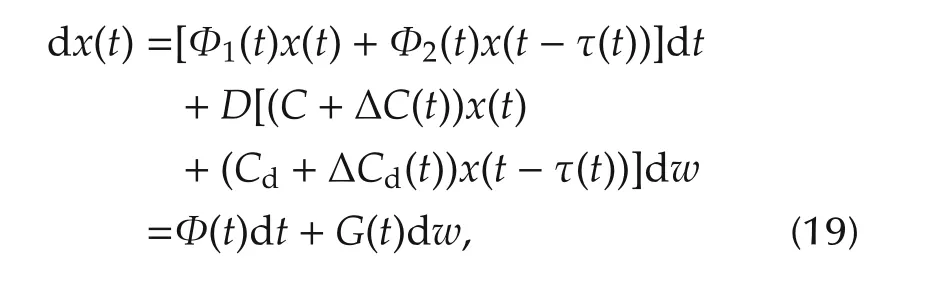
where

In view of(18),we select the control in(20)for the sliding mode controller as follows:

where ρ(t)is the switching gain,us(t)is the switching control part,that is also able to overcome the system uncertainties in sliding mode control,and sgn(·)is the sign function.

Due to ueqc(t)≠ueq(t)for the uncertain system(unnominal system),the states cannot retain on the switching surface.However,us(t)can force the state vector toward s(t)=0.Therefore,the total control input(20)can hold the states within a certain range around the switching surface.

Remark 2 Without loss of generality,we assume that x(t− τ(t))is known by the controller,either for the case of known time delay τ(t)as a time trigger signal,or for the case of unknown time delay but as an event trigger signal.The latter means that the value of τ(t)may not need to be exactly known,while the value x(t−τ(t))is known or received.

Remark 3 In(14),the condition of GB=BTXB nonsigular needs matrix B to be a full-column rank matrix.It is because X is a non-singular matrix.The condition GD=BTXD=0 implies that D is not a full rank matrix.In practical applications,we may release this constraint by choosing the trace of GD to be a much small value.

TheSMCdesignneedstoachievetwogoals:i)thesystem states trajectory should globally reach the switching surfaces s(t)=0,i.e.,s(t)˙s(t)＜0,and ii)the system dynamics(19)on the switching surface is robustly stochastically stable.We address these two goals in the following sections.

3.3 Robust sliding mode control via LMI approach

Based on the above SVD for uncertainty structures in Section 3.1,we derive the following stability theorems.Theorem 1 was presented in[29]without the proof.

Theorem 1 System(1)–(2)with control(18)and ˙τ(t)≤h＜1 is robustly stochastically stable,if there exist positive definite matrices X and Q,and positive adjustable scalars ∈1i,∈2j,∈3,∈4i,∈5j(i=1,...,lAand j=1,...,lAd)satisfying

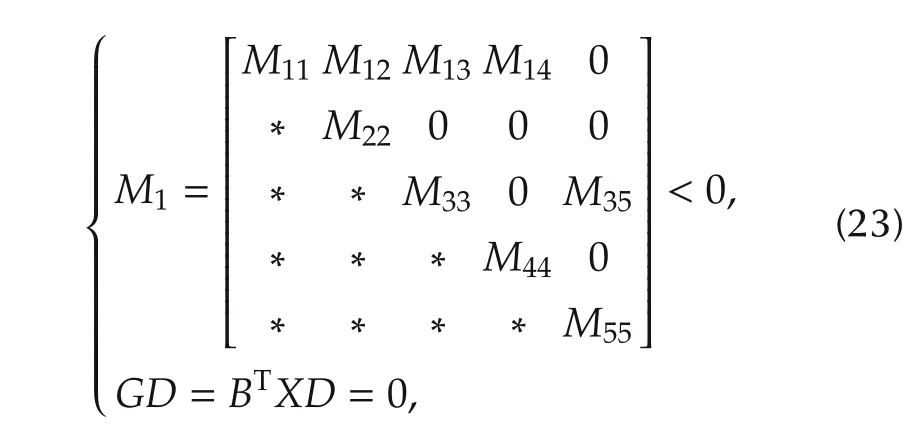
where matrix M1is a symmetric matrix with symbol“*”as its symmetric part for simplicity,

and JC,RC(t),UC,Jcd,RCd(t),UCdare in(10)–(13).

Denote

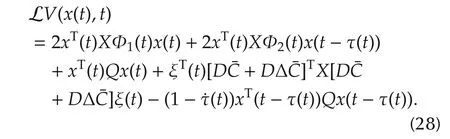
For any ε1i＞ 0,i=1,...,lAand ε2j＞ 0,j=1,...,lAd,the following matrix inequalities(29)–(30)hold in view of(3)–(13)and(17),in addition to[21]:

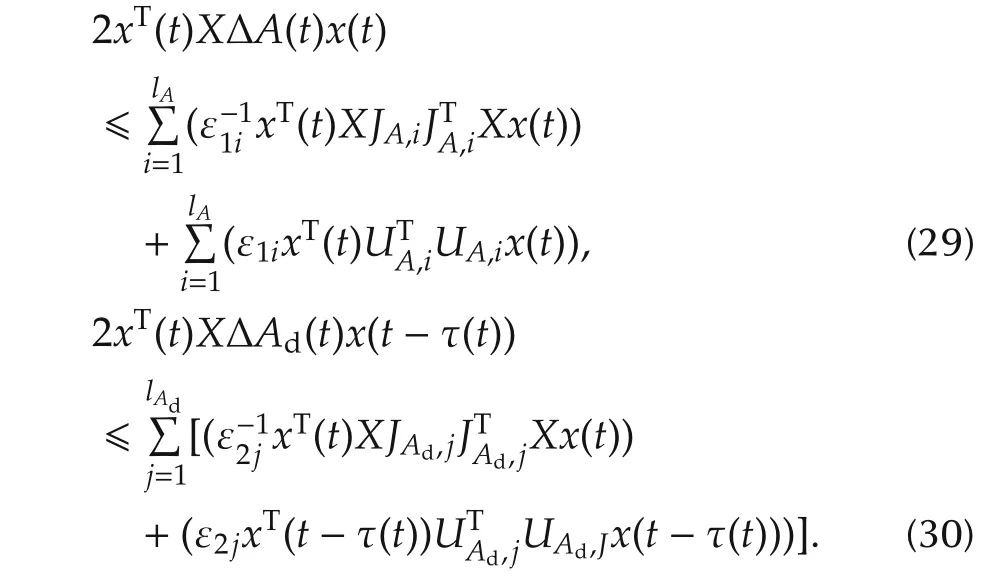
In(24),let Π3＞ 0.By selecting a suitable ε3＞ 0,we have the following inequality from Lemma 2:

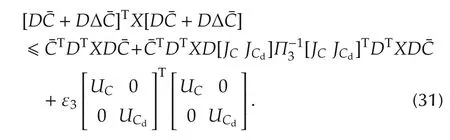
Substituting(29)–(31)intoLV(x(t),t)andapplyingLemma 1,we have

where

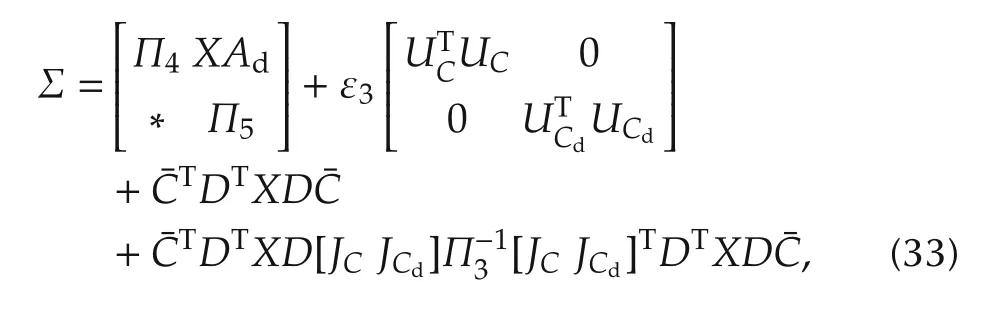
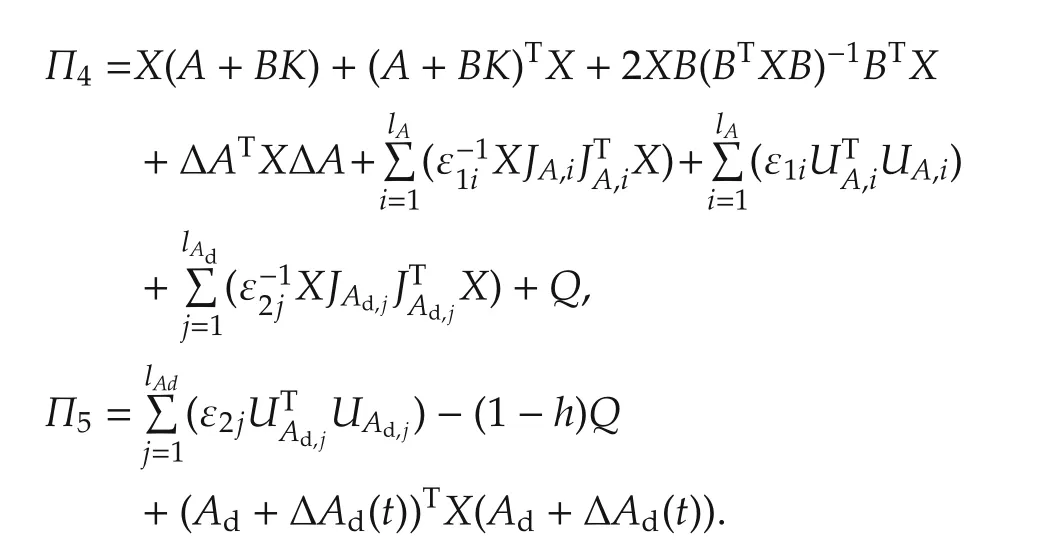
Since−X ＜0,by applying Lemma 1 again,inequality Σ＜0(33)is equivalent to

where

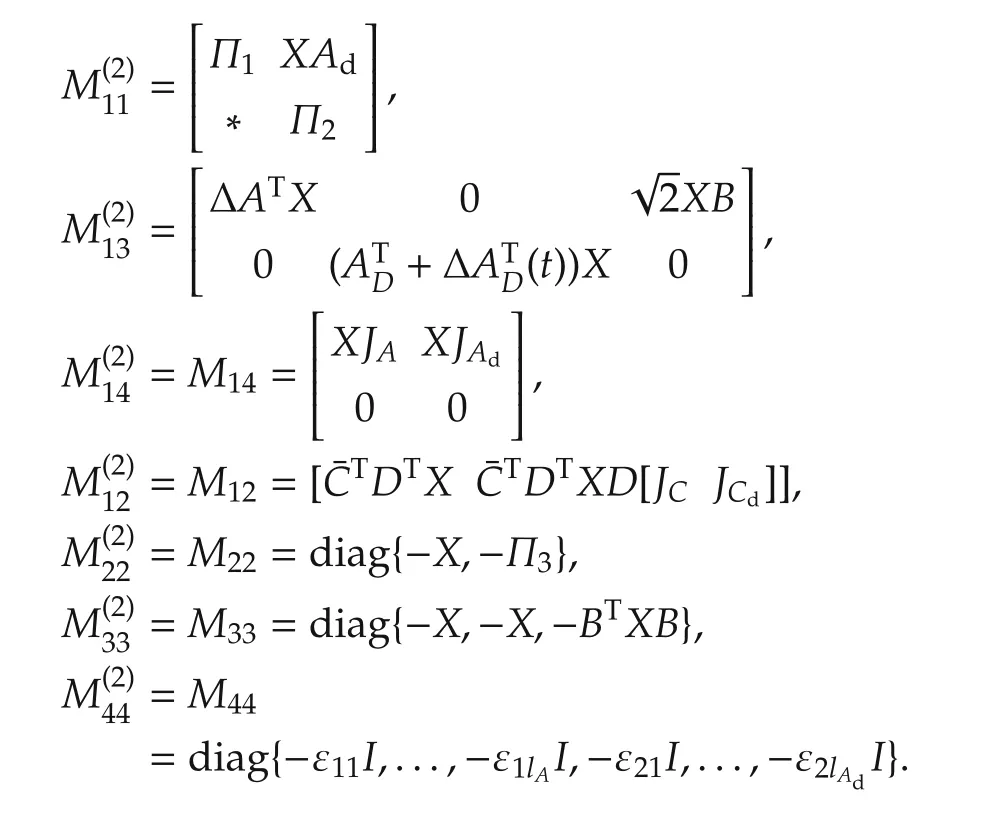
The uncertain part of matrix M2satisfies

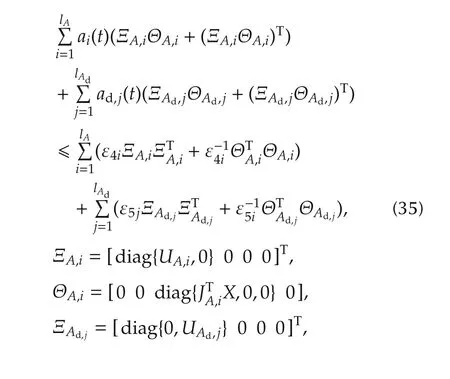
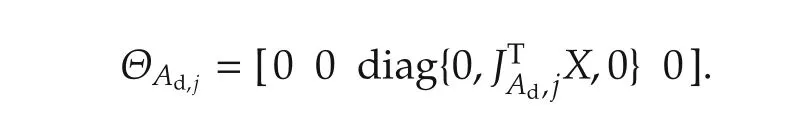
Therefore,we have inequality(36)from(34)–(35):

where

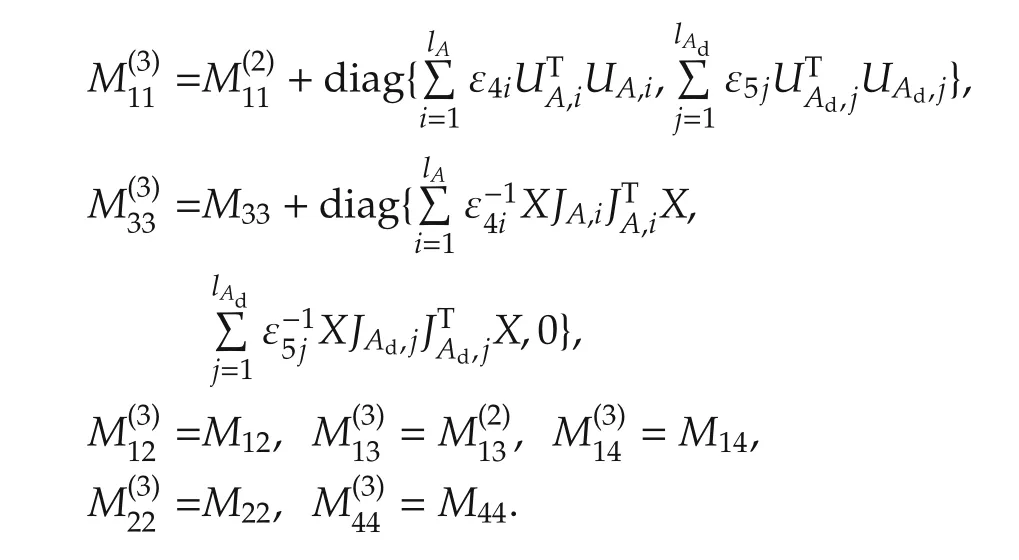
Then,LMI M3＜0,is equivalent to M1＜0,by Lemma 1.It completes the proof.

3.4 Controller and reachability analysis

Here we design the controller to globally drive the systemstates trajectory totheswitchingsurface in probability 1 as Theorem 2(in[29]without proof).

Theorem 2 The reachability in probability 1 to the switchingsurfaces(t)=0forthestatesofsystem(1)–(2)can be guaranteed by controller(20)with ρ(t)as

because of‖s(t)‖1≥ ‖s(t)‖.By substituting ρ(t)in(37)into(38),we have˙Vs≤−λ‖s(t)‖＜0 if s(t)≠0,because λ ＞ 0.Thus,the control in(20)–(22)with ρ(t)in(37)guarantees the system states toward the switching surface s(t)=0 in probability 1.

Theorem 2 states that the state vector of system(1)–(2)will globally be driven to the pre-determined switching surface s(t)=0 by the control in(20)–(22)and(37)in probability 1.

In this paper,to reduce the chatter,we choose another form of λ as

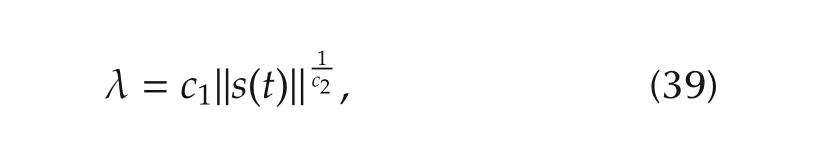
where c1and c2are positive constants.As the state vectorisclosetos(t)=0,λmayalsobereducedin(39),and not as constant,that leads to small chatter amplitudes.

4 Comparison

In the above sections,we have described the structural uncertainties in a practical and flexible form,and introduced the SVD,a group of adjustable parameters for uncertainties,and Theorem 1 to easily find the available matrix X by the LMI for the controller design.

It should be noticed that the description of structural uncertainties in(3)–(6)or(10)–(13)(e.g.,ΔA(t)=may seem to have relation with the EF(t)H form as commonly used in H∞control[21–23,28,30,33].However,as shown in[25,27]they are not equivalent because the common EFH form binds different structural uncertainties,e.g.,ΔA,ΔAd,ΔB and/or so on,that lead to conservatism and large size matrices.Furthermore,their matrices E and H are not from the SVD.Thus,the proposed treatment makes difference and leads to less conservative results.

To show the advantage of the method,we compare the methods with and without this SVD treatment by a theoretical analysis as follows.To avoid the confliction of variable names,the variable names for the methods without the SVD treatment are marked with"～"on the head.

Theorem 3 Consider the system in(1)and the normal structural uncertainties as described as in EF(t)H format as

Then,we may have

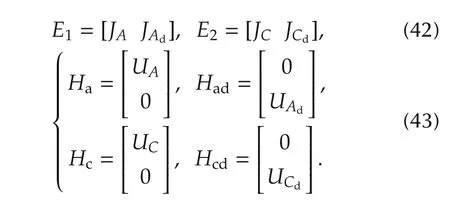
The method without SVD in(40)–(41)may be observed as a special case of the proposed method with the SVD treatment in our Theorem 1 as

Proof The proof is to substitute scalars ε1i,ε2j,ε3,ε4i,ε5j(i=1,...,lAand j=1,...,lAd)with˜ε1,˜ε2,˜ε3,and˜ε4in(44)into(23)of Theorem 1.Then,it is reduced to the case exactly as the one without the SVD treatment on each uncertain structure in(3)–(6).It shows that the treatment without the SVD as in(40)–(41)is a special case of the method in Theorem 1 with“the SVD treatment”by a restriction as in(44).

Remark4 Theorem3clearlyshowsthatthemethod without the SVD treatment has restrictions on the adjustableparametersformatricesΔAandΔAd.However,our new method treats them by various adjustable parameters:i)ε1i,i=1,...,lA,instead of one˜ε1,ii)ε2j,j=1,...,lAdinstead of one˜ε2,and iii)ε4i,i=1,...,lA,and ε5j,j=1,...,lAd,instead of one˜ε4.Even for a very special situation,e.g.,lA=1 and lAd=1,the proposed method is still more flexible in view of ε4and ε5for ΔA and ΔAd,respectively,to replace one˜ε4for both ΔA and ΔAd.

Remark 5 When the considered system is without the Brownian motion but with the time-varying delay,the method presented here is still valid and flexible with less conservatism.

5 Example

In this section,we present an example to show the proposed method.The considered system is in(1)with

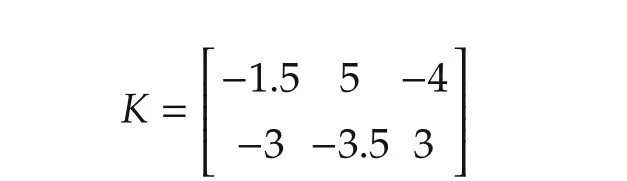
as in[29].However,in order to further show our new results,this section mainly contains new figures with random seeds 1 and 2 that are not published in[29].Matrices JA,JAd,JC,JCd,UA,UAd,UCand UCdare calculated by the SVD method as in(10)–(13).Theorem 1 can find solution of X and Q for stability by “mincx”solver in MATLAB[34].We also choosethe chatter of control signal u(t)is significantly reduced.

In simulation,we take the initial value Δx(t)=[0.6 0.2 −1]T,t∈ [−1,0],and the simulation time as[0,3]seconds.The simulation results are shown in the following figures.Three different Brownian motions of w(t)are randomly generated by random seeds 1,2 and 3.Fig.1 is the system state trajectory with various w(t)in random seeds 1,2,3.Figs.2 and 3 show s(t)and u(t)in random seed 1,respectively.Figs.4 and 5 show s(t)and u(t)in random seed 2.It clearly shows that the system does well converge to stable states with good performance by the proposed SMC via SVD treatment on the uncertainties.

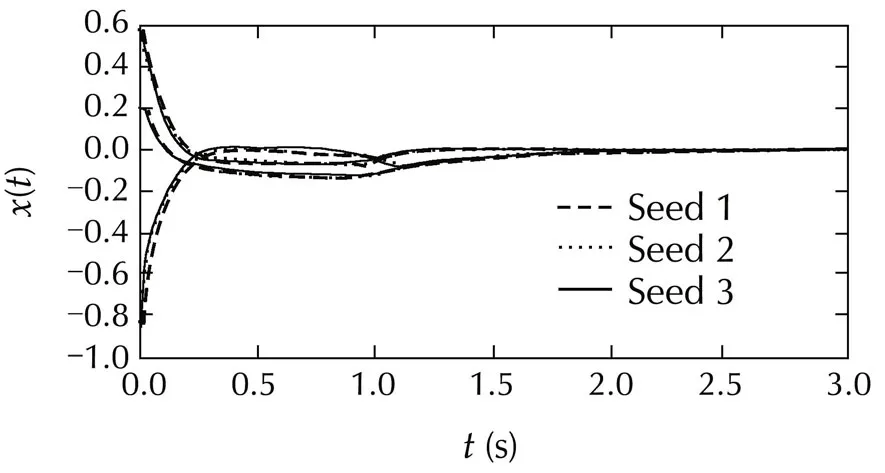
Fig.1 Trajectory x(t)with various w(t)in random seeds 1,2,3[29].

Fig.2 s(t)with a flexible λ and a w(t)in random seed 1.

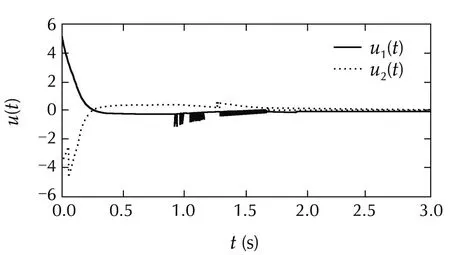
Fig.3 u(t)with a flexible λ and a w(t)in random seed 1.

Fig.4 s(t)with a flexible λ and a w(t)in random seed 2.

Fig.5 u(t)with a flexible λ and a w(t)in random seed 2.

6 Conclusions

In this paper,a flexible robust SMC method with the SVD treatment on the structured uncertainties is developed for general uncertain stochastic systems with time-varying delay and structural uncertainties.It is theoretically proved that the conservatism is reduced.The proposed robust control can globally drive the state trajectories toward the preselected switching surface in probability 1.The example validates the theoretical results.It is noticed that the discussed problem in this paper is with the derivative of the time-varying delay τ(t)not larger than one as common in the literature.However,it is interesting to develop the new results for the cases with τ′(t)＞ 1.We have had it as in[35]which is submitted separately.

Acknowledgements

TheauthorswouldliketothankProf.JamesLamatthe University of Hong Kong and Prof.Daniel Ho at the City University of Hong Kong for their helpful discussion.

[1]J.Chiasson,J.J.Loisean.Application of Time Delay Systems.1st ed.London:Springer,2007.

[2]P.F.Hokayem,M.W.Spong.Bilateralteleoperation:anhistorical survey.Automatica,2006,42(12):2035–2057.

[3]A.D.Zeitlin,M.P.McLaughlin.Safety of cooperative collision avoidance for unmanned aircraft.Proceedings of the 25th Digital Avionics Systems Conference.Piscataway:IEEE,2006:868–874.

[4]J.Kaloust,C.Ham,J.Siehling.Nonlinear robust control design for levitation and propulsion of a maglev system.IEE Proceedings-Control Theory and Applications,2004,151(4):460–464.

[5]R.Brooks.A robust layered control system for a mobile robot.IEEE Journal of Robotics and Automation,1986,2(1):14–23.

[6]T.Umeno,Y.Hori.Robust speed control of DC servomotors using modern two degrees-of-freedom controller design.IEEE Transactions on Industrial Electronics,1991,38(5):363–368.

[7]P.Shi,G.Liu,D.Rees,et al.Active disturbance rejection control for uncertain multivariable systems with time-delay.IET Control Theory&Applications,2007,1(1):75–81.

[8]B.Du,J.Lam,Y.Zou,et al.Stability and stabilization for Markovian jump time-delay systems with partially unknown transition rates.IEEE Transactions on Circuits and Systems–I:Regular Papers,2013,60(2):341–351.

[9]M.Y.Chow,Y.Tipsuwan.Network-based control systems:a tutorial.Proceedings of the 27th Annual Conference of the IEEE Industrial Electronics Society.Piscataway:IEEE,2001:1593–1602.

[10]E.Fridman,U.Shaked.Special issue on time-delay systems.International Journal of Robust and Nonlinear Control,2003,13(9):791–792.

[11]Y.Liu,B.Xu,B.Shi.Kalman filtering for stochastic systems with consecutive packet losses and measurement time delays.Control Theory&Applications,2013,30(7):898–908.

[12]Y.Fu,Z.Tian,S.Shi.Output feedback stabilization for stochastic time-delay nonlinear systems.Control Theory&Applications,2003,20(5):749–752.

[13]Q.Wang,R.F.Stengel.Robust nonlinear control of a hypersonic aircraft.JournalofGuidance,Control,andDynamics,2000,23(4):577–585.

[14]A.Kuperman,Q.C.Zhong.Robust control of uncertain nonlinear systems with state delays based on an uncertainty and disturbance estimator.International Journal of Robust and Nonlinear Control,2011,21(1):79–92.

[15]S.Xu,P.Shi,Y.Chu.Robust stochastic stabilization and H∞control of uncertain neutral stochastic time-delay systems.Journal of Mathematical Analysis and Applications,2006,314(1):1–16.

[16]P.Shi,X.Luan,F.Liu.H∞filtering for discrete-time systems with stochastic incomplete measurement and mixed delays.IEEE Transactions on Industrial Electronics,2012,59(6):2732–2739.

[17]V.I.Utkin.Slidingmodecontroldesign principlesand applications to electric drives.IEEE Transactions on Industrial Electronics,1993,40(1):23–36.

[18]Y.H.Roh,J.H.Oh.Robust stabilization of uncertain inputdelay systems by sliding mode control with delay compensation.Automatica,1999,35(11):1861–1865.

[19]Y.Xia,Y.Jia.Robust sliding-mode control for uncertain timedelay systems:an LMI approach.IEEE Transactions on Automatic Control,2003,48(6):1086–1091.

[20]M.Liu,P.Shi,L.Zhang,et al.Fault-tolerant control for nonlinear Markovian jump systems via proportional and derivative sliding mode observer technique.IEEE Transactions on Circuits and Systems–I,2011,58(11):2755–2764.

[21]Y.Niu,D.Ho,J.Lam.Robust integral sliding mode control for uncertain stochastic systems with time-varying delay.Automatica,2005,41(5):873–880.

[22]L.Yu,J.Chu.AnLMIapproachtoguaranteedcostcontroloflinear uncertain time-delay systems.Automatica,1999,35(6):1155–1159.

[23]C.E.de Souze,X.Li.Delay-dependent robust H∞control of uncertain linear state-delayed systems.Automatica,1999,35(7):1313–1321.

[24]L.Wu,X.Su,P.Shi.Sliding mode control with bounded L2gain performance of Markovian jump singular time-delay systems.Automatica,2012,48(8):1929–1933.

[25]S.Wang,H.Y.Yeh,P.Roschke.Robust control for structural systems with parametric and unstructured uncertainties.Journal of Vibration and Control,2001,7(5):753–772.

[26]S.Wang,L.S.Shieh,J.W.Sunkel.Robustoptimalpole-placement in a vertical strip and disturbance rejection.Proceedings of the 32nd IEEE Conference on Decision and Control.San Antonio:IEEE,1993:1134–1139.

[27]S.Wang,S.Lin,L.S.Shieh,et al.Observer based controller for robust pole clustering in a vertical strip and disturbance rejection in structured uncertain systems.International Journal of Robust and Nonlinear Control,1998,8(12):1073–1084.

[28]K.Zhou,P.P.Khargonekar,J.Stousrup,etal.Robust performance of systems with structured uncertainties in state space.Automatica,1995,31(2):249–255.

[29]S.Wang,L.Bai.Flexible robust sliding mode control for uncertain stochastic systems with time-varying delay and structural uncertainties.Proceedings of the 51st IEEE Annual Conference on Decision and Control.New York:IEEE,2012:1536–1541.

[30]S.Xu,T.Chen.Robust H∞control for uncertain stochastic systems with state delay.IEEE Transactions on Automatic Control,2002,47(12):2089–2094.

[31]I.Schur.¨Uber Potenzreihen,die im Innern des Einheitskreises beschr¨anktsind.Journalf¨urdiereineundangewandte Mathematik,1917,1917(147):205–232.

[32]S.Wang.Robust active control for uncertain structural systems with acceleration sensors.Journal of Structural Control,2003,10(1):59–76.

[33]L.Xie,M.Fu,C.E.de Souza.H∞control and quadratic stabilization of systems with parameter uncertainty via output feedback.IEEE Transactions on Automatica Control,1992,37(8):1253–1256.

[34]P.Gahinet,A.Nemirovski,A.J.Laub,et al.LMI Control Toolbox.1995:http://www.mathworks.de/help/releases/R13sp2/pdf_doc/lmi/lmi.pdf.

[35]S.Wang.New Lyapunov-type Functional for General Stochastic Systems with Time-varying Delay.Technical note.Charlotte:UNC Charlotte,2013.

Sheng-Guo WANG received the B.Sc.and M.Sc.in Electrical Engineering from University of Science and Technology of China in 1967 and 1981,respectively,and the Ph.D.in Electrical&Computer Engineering from University of Houston in 1994.He is a professor at University of North Carolina at Charlotte.He has published more than 100 papers in journals and conferences,and been the PI for numerous research projects since 1974.His research work has been supported by NSF,NCDOT,Tellabs,HP,Agilent,NASA,ARO,British Council,and China Railway.He is a frequent reviewer for more than 30 international journals and more than 10 international conferences.He has served as a program committee member(IPC)for more than 20 times,e.g.,2000 ACC;2000 SPIE;2005 BISBC;2006 SICE-ICCAS;2007 CBGI;2007–2009,2011 ISC;2009 IEEE ISIC;2010 IEEE CCA;2012 ICEE;2007,2008,2010–2014 IEEE ICCAS,an invited session organizer for 2000 ACC,and more than 10 times as Session Chair/Co-chair for international conferences,e.g.,IEEE CDC,WCICA,ACC and IFAC-WC.He has also served as an associate editor for JDSMC,JCTT,and IEEE MSC,etc.His current research interests include systems,control,circuits,modeling,robust control,GIS,big data,communications,computer networks,mathematical and numerical analysis,algorithms,applications.

Prof.WangisarecipientofChinaNationalScienceConferencePrize 1978 and many other academic awards,including the Best Session Paper Presentation Award of 2001 ACC,the inventor award for UNC Charlotte Invention 2001,an Outstanding Faculty Award at Prairie View A&M University 1997,Sigma Xi Research Excellence Award(UH Chapter)1994,British Council Scholarship 1989.His membership includes IEEE,ASME,ASEE,Sigma Xi,and Tau Beta Pi.E-mail:swang@uncc.edu.

2 May 2014;revised 14 November 2014;accepted 17 November 2014

†Corresponding author.

E-mail:swang@uncc.edu.Tel.:+1-(704)687-5063;fax:+1-(704)687-7803.

This work was partially supported by the National Science Foundation Grants(Nos.0940662,1115564)of Prof.S.-G.Wang.

©2014 South China University of Technology,Academy of Mathematics and Systems Science,CAS,and Springer-Verlag Berlin Heidelberg

Mingzhi CHEN received the B.Sc.degree in Computer Networks from Fuzhou University,Fuzhou,China in 2003,M.Sc.degree in Computer Software and Theory,and Ph.D.degree in Communication and Information Systems from Fuzhou University,Fuzhou,China in 2005 and 2010,respectively.He had been working at the University of North Carolina at Charlotte,U.S.A.as a postdoctoral fellow from August 2012 to September 2013.Currently,he is working at Fuzhou University as an associate professor.His current research interests include intelligent information processing and information security.E-mail:mchen@fzu.edu.cn.