Adaptive-backstepping force/motion control for mobile-manipulator robot based on fuzzy CMAC neural networks

Thang-Long MAI,Yaonan WANG

1.College of Electrical and Information Engineering,Hunan University,Changsha Hunan 410082,China;

2.Faculty of Electronics Engineering,Industrial University of Hochiminh City,Hochiminh City,Vietnam

Adaptive-backstepping force/motion control for mobile-manipulator robot based on fuzzy CMAC neural networks

Thang-Long MAI1,2†,Yaonan WANG1

1.College of Electrical and Information Engineering,Hunan University,Changsha Hunan 410082,China;

2.Faculty of Electronics Engineering,Industrial University of Hochiminh City,Hochiminh City,Vietnam

Inthispaper,anadaptivebacksteppingfuzzycerebellar-model-articulation-controlneural-networkscontrol(ABFCNC)system for motion/force control of the mobile-manipulator robot(MMR)is proposed.By applying the ABFCNC in the tracking-position controller,the unknown dynamics and parameter variation problems of the MMR control system are relaxed.In addition,an adaptive robust compensator is proposed to eliminate uncertainties that consist of approximation errors,uncertain disturbances.Based on the tracking position-ABFCNC design,an adaptive robust control strategy is also developed for the nonholonomicconstraint force of the MMR.The design of adaptive-online learning algorithms is obtained by using the Lyapunov stability theorem.Therefore,the proposed method proves that it not only can guarantee the stability and robustness but also the tracking performances of the MMR control system.The effectiveness and robustness of the proposed control system are verified by comparative simulation results.

Backstepping control;Fuzzy CMAC(cerebellar model articulation controller)neural networks;Adaptive robust control;Mobile-manipulator robot

DOI10.1007/s11768-014-3181-4

1 Introduction

The applications of the mobile-manipulator robot(MMR)could be found in construction,mining,and planetarysciences.TheMMRconsistsofarmsandamobile platform with kinematic and dynamic constraints,which make it a highly coupled dynamic nonlinear system.Therefore,the traditional model-based feedback control methods[1–3]are not easy to apply in the MMR control system.However,the control of the MMR,withuncertainties,is necessary in many practical applications,and the adaptive control schemes have exhibited good properties as an attempt to cope with this problem[4–7].

In the recent years,the adaptive model-free controllers-based fuzzy/neural networks(NNs)have also been appliedtodealwiththeuncertaindynamicsoftheMMR.The NNs,with the self-learning characteristic,good approximationcapability[8,9],aretheusefultechniquefor robotic control systems[10–13].Lin and Goldenberg[9]proposed an adaptive NNs controller to identify online the dynamics and eliminate disturbances of the MMR control system.However,the parameters of the Gaussian function in this scheme were chosen a priori and kept fixed[10,11].The authors in[13]have developed a modular fuzzy navigation method in changing and dynamic unstructured environments.In this method[13],an integration of robust controller and modified Elman NNs is to deal with uncertainties.However,this method[13]still contained the drawbacks of previous methods in requiring the knowledge of the bounded parameters.

Recently,cerebellar model articulation controller(CMAC)has been developed rapidly.It is an autoassociative memory feedforward NNs with overlapping receptive fields[14].The CMAC has already demonstrated favorable features,such as fast learning,good generalization capability and simplicity of computation[15,16],when compared with the NNs.In the controllers-based Fuzzy CMAC(FCMAC)[17–19],the control performance can be enhanced by programming the appropriate membership-function rather than modifying the partition size to increase the computation burden.

In the past decade,the backstepping control system(BCS)has been widely exploited in a variety of applications in robotic control systems[20–23].The main advantageoftheBCSisrepresentedbykeepingtherobustness properties with respect to the uncertainties[20].For the MMR control,the authors in[21]proposed the backstepping technique and the filtered-error method to construct the nonlinear tracking control laws for the MMR.Although the laws of this method were obtained by the Lyapunov theory to guarantee the stability of the controlled system,but the un-modeled dynamics and external disturbances were not considered.The intelligent techniques,such as the fuzzy and NNs,have been proven to be a good candidate for enhancing the ability and overcoming the defects of the recursive backstepping design methodology[22,23].

In this study,a novel fuzzy CMAC NNs(FCNs)is proposed,which incorporates the highlighted properties of thefuzzytechnique,andtheCMAC.TheTakagi-Sugeno-Kang(TSK)[24,25]technique is incorporated with the CMAC structure,and this TSK-FCNs structure is different from the previous FCMAC structure[17–19].In the proposed TSK-FCNs structure,the rule-base contains the CMAC structure with layers and blocks,and it is a generalization of the conventional fuzzy system.Thus,the CMAC in the proposed FCNs structure is related to a fuzzy rule-base.With this feature,the proposed TSKFCNs can solve the constant output-weights problem of the FCMAC structures[17–19].

The purpose of this study is to design an intelligent control system by inheriting the advantage of the conventional BCS to achieve the high-position tracking for the MMR control system.Therefore,in the proposed method,the FCNs are applied in the tracking-position ABFCNC-system to deal with unknown highly coupled dynamics of the MMR control system.Here,this approachisalsotoimprovetheflexibilityandcontrolspeed of the previous controllers-based NNs[10–13]for the MMR in the presence of various operating conditions.In addition,an adaptive-robust compensator is also proposed to solve the aforementioned drawbacks of the previous methods[10–13],such as the inevitable approximation errors,disturbances and the requirement for prior knowledge of the controlled system.Besides the position controller,the constraint-force control is also considered by an adaptive robust law.The onlinelearning algorithms of the controller-parameters are obtained by the Lyapunov theorem such that the stability of the controlled system is guaranteed.

Therestofthepaperisorganizedasfollows.Section2 describes the properties of the MMR,the backstepping controller and the structure of the FCNs.In Section 3,the adaptive control algorithm is presented.The comparative simulation results for MMR are described in Section 4.Finally,conclusion is drawn in Section 5.

2 Preliminaries

2.1 System description

The dynamics of MMR system can be considered as the dynamics of an n-degree of freedom manipulators mounted on a mobile platform that can be expressed as a Lagrange function of the following form[5,6]:

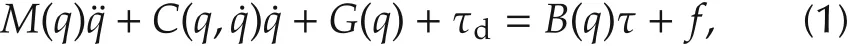
and m-kinematic constraints are described by

where q,˙q,¨q∈Rn×1are the joint position vector,velocity vector and acceleration vector,respectively.M(q)∈Rn×nis the inertia matrix.C(q,˙q)˙q∈Rn×1expresses the vector of centripetal and coriolis torques.G(q) ∈ Rn×1is the gravity vector. τd∈ Rn×1is unknown disturbances.τ ∈ Rr×1is the torque input vector.r=n − m,B(q)∈ Rn×ris the input transformation matrix.f=A(q)Tγ,A(q)∈ Rm×nis the full rank matrix.γ ∈ Rm×1isthevectorLagrangianmultiplier,n,m,r∈ N.For convenience,a mobile 3-DOF manipulators robot,as shown in Fig.1,is applied to verify dynamics properties that are given in Section 4.

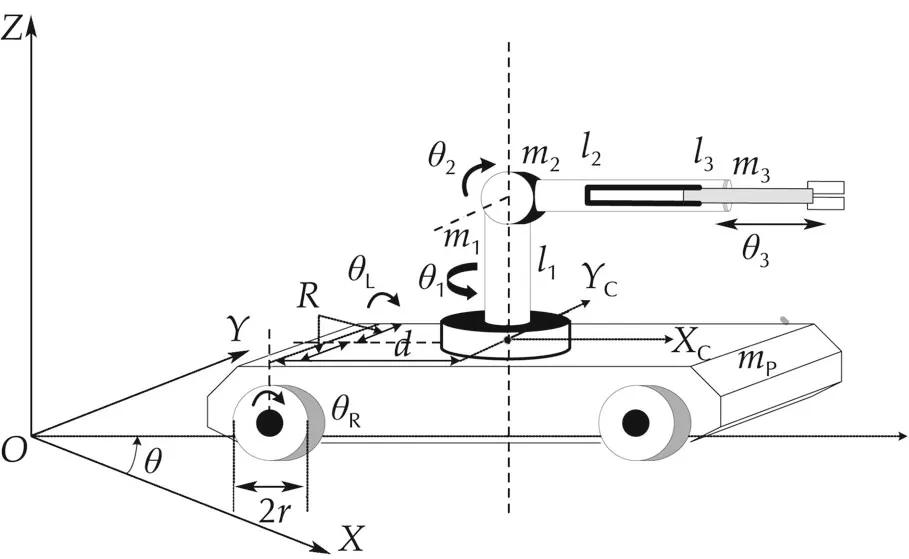
Fig.1 The 3-DOF mobile manipulator robot model.

In our study,we assume that the MMR is subject to nonholonomic constraints.Thus,the dynamics of the MMR(1)can be expressed in the following forms[5,6]:

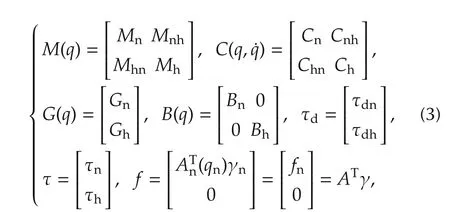
From the above analysis,(2)can be expressed as

where ZT(qn)Z(qn)is also a full-rank matrix.From(4)and(5),there exists a vector ρ and its derivation˙ρ satisfies

Following(8),the dynamics of the MMR system(1)can be rewritten as the following form[5,6]:

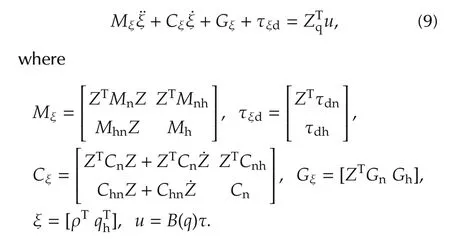
The nonholonomic-force multiplier γncan be obtained by(9)

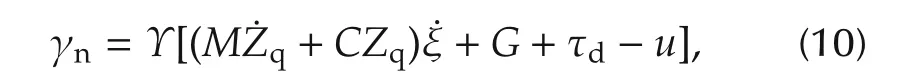
where Υ =(AM−1AT)−1AM−1.

Property 1 M is a uniformly bounded and continuous[5].

Property 2 Mξis a positive definite symmetricmatrix,Mξis uniformly bounded:mξ1‖x‖2≤ xTMξx ≤mξ2‖x‖2,∀x ∈ R(n−m)×1,where mξ1and mξ2denote the minimum and maximum eigenvalues of Mξ,respectively[5].

Property 3Skew-symmetric matrix[5]:Sξ≡˙Mξ−2Cξ,where Sξ(ξ,ξ)is a skew-symmetric matrix.

2.2 Backstepping controller

A conventional backstepping control system for the motion of the MMR is developed to assist and provide an essential background for the design of the proposed controller to be introduced in the next section.Given a desired position trajectory=We will designabacksteppingcontrollersothat=tracksThe(t)is assumed to be bounded and uniformly continuous.It also has bounded and uniformly continuous derivatives up to the second orders.

In this study,a decoupling-control scheme is introduced to control the generalized position and the constraint force,separately.Thus,the control input u is considered in the following form[5]:

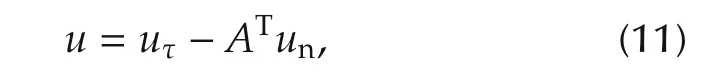
where two terms on the right side of equation(11)are the backstepping control inputs for the torque and the nonholonomic-constraint force.The detailed structure of the position-backstepping controller is described step-by-step as follows:

Step 1 Define a tracking error vector eξ1(t)as

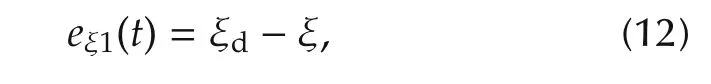
and its derivative as

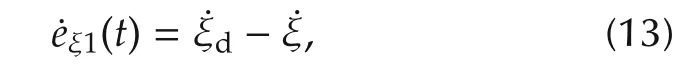
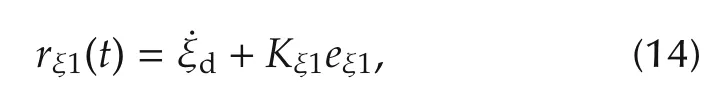
where Kξ1is the positive constant matrix.The first Lyapunov function is chosen as the following form:

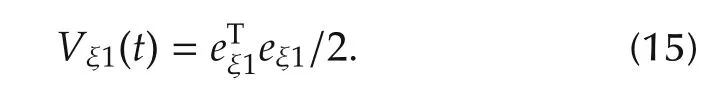
Define the following vector:

Then the derivative of Vξ1(t)can be represented as

Step 2 The derivative of eξ2can be expressed as

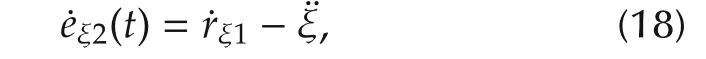
where¨ξcan be viewed as the second virtual controlinput.By using(12)–(14),(16)and(18),then,(9)can be rewritten as follows:

Define the second Lyapunov function as the following form:

Then,the derivative of Vξ2(t)can be represented as

By using(19),then,(21)can be expressed as

where yc=Mξ˙rξ1+Cξrξ1+Gξ.

Step 3 If the dynamics of the MMR are exactly known,then the position-backstepping controller can be designed in the following form:

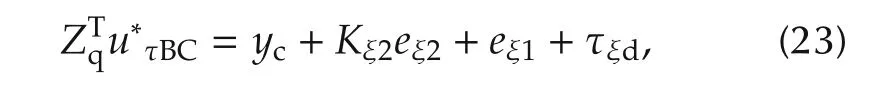
where Kξ2is a positive constant matrix.By substituting(23)into(22),we can obtain the following inequality:

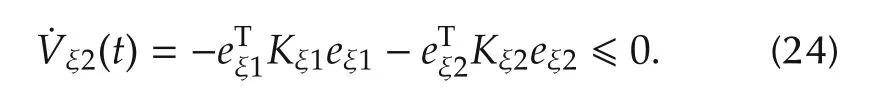
As can be seen from(23),˙Vξ2(t)≤0.Therefore,the stability of the position-backstepping controller system can be guaranteed[26].Unfortunately,this positionbackstepping controller requires the detailed dynamics of the MMR that cannot be exactly obtained.Thus,the FCNs will be proposed in the next section to deal with this drawback.

2.3 The structure of FCNs

The proposed FCNs’strategy is to combine the TSK-fuzzysystem with andCMAC.Fig.2showsthe structure of the proposed FCNs,which is explained as follows.

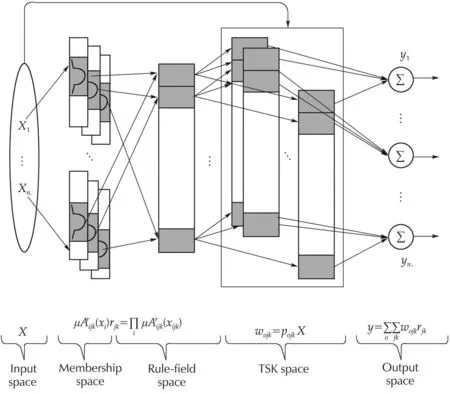
Fig.2 Architecture of the FCNs.

with j=1,...,nl,k=1,...,nb,i=1,...,ni,r=1,...,nr,o=1,...,no,ni,nl,nb,nr,no∈N.niis the number of inputs(input dimension),nlis the number of layers for each input,nbis the number of blocks for each layer,nois the number of outputs,nris the number of fuzzy rules and nr=nlnb.xiis the fuzzy input ith,is the fuzzy membership function for the ith input,jth layer,kth block,wojkis the TSK-type outputweight for oth TSK fuzzy output.is the adjustable factor of consequence part of fuzzy rules.This dynamic TSK-FCNs model is composed of the input,membership,rule-field,TSK-weights memory,and fuzzy-output spaces.The detail of the spaces is introduced as follows:

1)Input space.For given input signals X =where niis the number of input signals.X can be quantized into discrete regions and moved to the next space by the neurons.These regions are the elements/neurons and(resolution)is represented as the number of elements.

2)Membership space.In this space,some elements can be accumulated as a block,which is the Gaussian membershipfunction,iscalculated by the following formula:

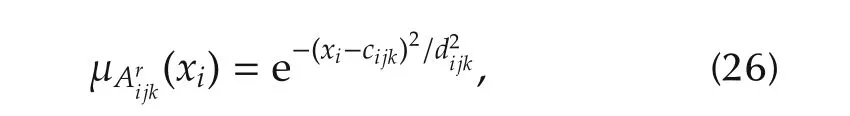
where dijkis the variance parameter,and cijkis the mean parameter.

3)Rule-field space(receptive field).Areas formed by blocks.Each block is presented as a rule-field.However,we use the AND operator to calculate outputs of this space

Operation of the product?can be referred to fuzzy inference mechanism and it is used to determine the firing strength.However,the multi-dimensional receptive field functions can be expressed in a vector form:

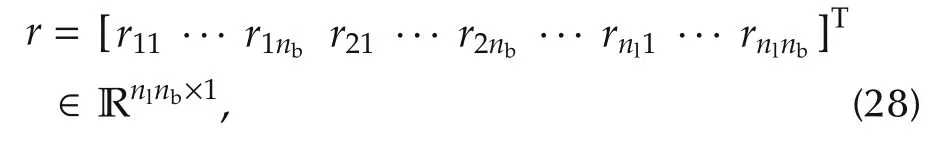
4)TSK space(TSK-weight memory).TSK layer describes the linear-combination functions in the consequent part of the fuzzy system.Moreover,the fuzzyweight memory can be described as

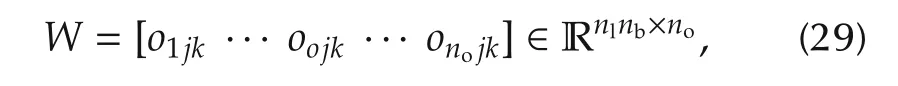
where oojk=[wo11···wo1nb···wonl1···wonlnb]T,o=1,...,no,no∈ N,oojk∈ Rnlnb×1.Moreover,following the definition of theTSK-fuzzy rule,wojkisdetermined as

where X=x1+x2+...+xni.

5)Output space.Each node in this layer expresses the output linguistic variable and it is computed as the summation of the activated weight with the rule-field space

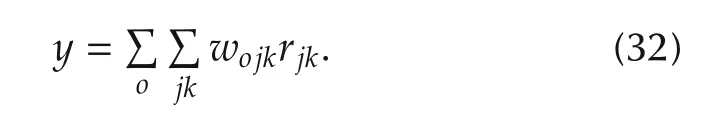
In addition,it can be denoted as

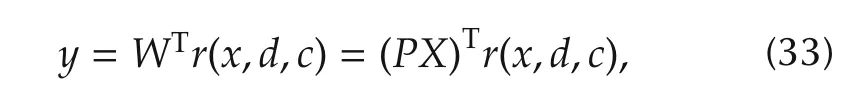
where d,c,P are the translation parameter vector,dilation parameter vector,and weight matrix,respectively.However,their vector forms are denoted as follows:

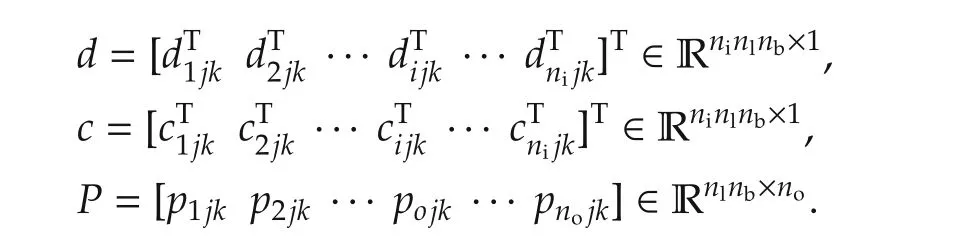
In this paper,we have no knowledge of the dynamic robotic system.Therefore,the proposed FCNs are applied to deal with unknown/uncertain dynamics of the mobile-manipulator robot.Based on the universal approximation error analysis,there exists an optimal FCNs structure with its optimal parameter such that[9]

where P＊,d＊,c＊are the optimal unknown parameters of the P,d,c,respectively,and Δ(x(t))is the approximation error vector.

Assumption 1 The norms of optimal weights are bounded ‖P＊‖≤ bP,‖d＊‖≤ bd,‖c＊‖≤ bc,where bP,bd,bcare the positive real values.

Assumption 2 Error of approximation process and disturbances of the robotic system are bounded:‖Δ‖≤bΔ,‖τod‖≤ τbo,where bΔ,τboare the positive real values.

3 Adaptive control algorithm

Follow the aforementioned analysis of the positiontrackingBCS,wefirstproposetheposition-trackingcontroller that combines the BCS and the FCNs.Then,the adaptive-robust controller for the constraint force will be developed.Fig.3 describes the structure of the proposed control system.The detailed procedure of our design is presented as follows.

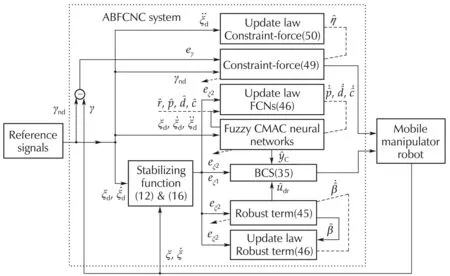
Fig.3 Diagram blocks of the control system.

3.1 Position tracking control design

The ideal BSC law in(23)depends on the unknown dynamics(1).Thus,the term ycwill be approximated by the proposed FCNs.The part τξdis the uncertain disturbances that may contain unstructured parts of the robot model.In addition,the approximation of FCNs will always generate the inevitable approximation errors.Therefore,a robust compensator will be proposed in order to estimate and compensate for τξdand approximation errors.An actual ABFCNC-torque control-law is proposed as

whereˆudris the robust term that is used to eliminate the approximation errors,unknown disturbances,unstructured parts of the robot model,the partˆycis the FCNs approximation function of the unknown function yc(22).According to(34),it can be represented as

By applying the position control law(35)to the dynamics of MMR(19),the closed-loop control system can be expressed as follows:

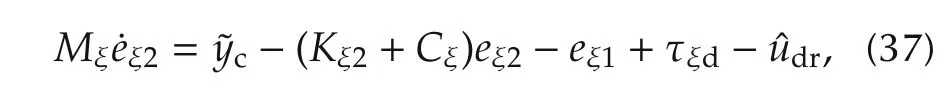
where the approximation error˜ycis defined as

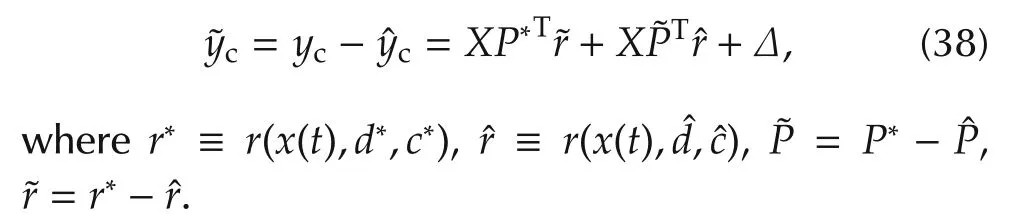
We can find that the closed-loop dynamic controlled system(38)from˜ycto eξ2is a state-strict passive system[9].The passivity is an important feature,which may guarantee the boundedness of the control system signals.In general,a hybrid-NNs controller cannot guarantee to be passive if we do not give an appropriate updating law for parameters of the networks.To achieve this,the linearization technique is applied to transform the nonlinear output of the FCNs function into a partially linear form[8]so that the Lyapunov theorem extension can be applied.Hence,we will take the expansion of˜r in a Taylor series to obtain

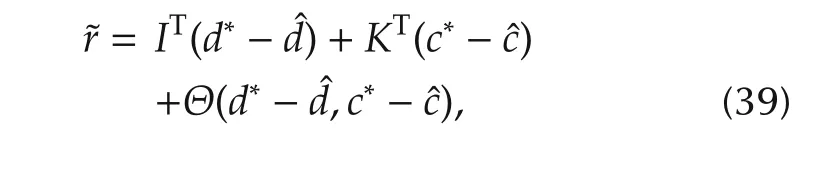
where Θ is the vector of higher-order terms in the Taylor series expansion,assume that I,K are bounded by the positive constants,

From(38)and(40),some simple steps of transform follow,and,we can obtain

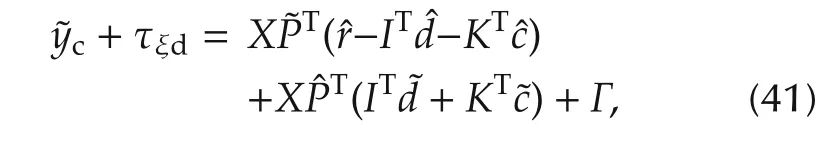
whereΓ=XP＊T(˜r+ITˆd+KTˆc)−XˆPT(ITd＊+KTc＊)+Δ+τξd.

By substituting(41)into(37),the closed-loop dynamics system can be rewritten as

Following Assumptions 1 and 2,the characteristic of the Gaussian function and(41),then,we can obtain the following inequality:

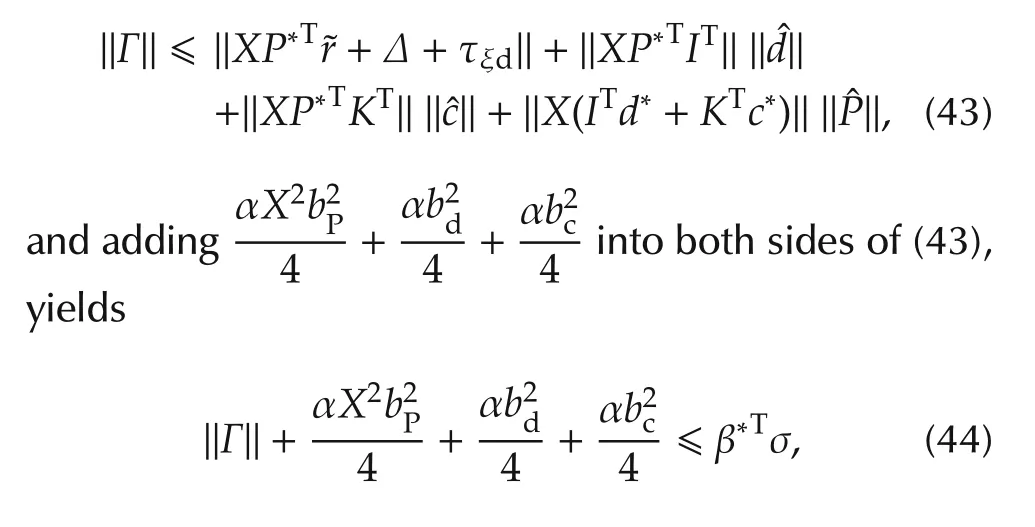
where β＊T=[β1β2β3β4],σT=[1‖ˆd‖‖ˆc‖‖ˆP‖],α is the positive constant,β1,β2,β3,β4are the positive constants,and they are uncertain bounds ofrespectively.

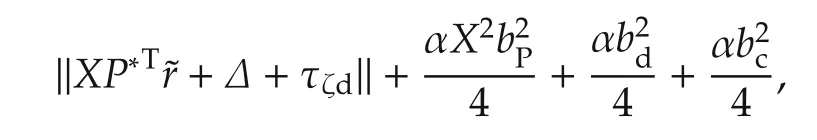
In order to guarantee the stability of system(42),the robust termˆudrmust eliminate the part Γ.Therefore,the robust termˆudris used to estimate the uncertain bound β＊Tσ,which is proposed as

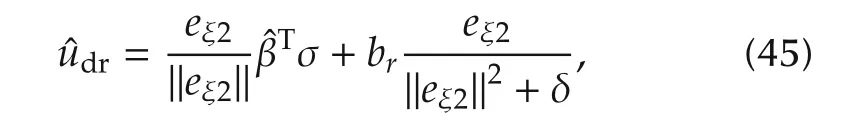
where brand δ are the positive constants,ˆβ is an estimated value of β＊.

Based on the above analysis,the adaptive-learning algorithms of the FCNs controller and the robust term are proposed as follows:

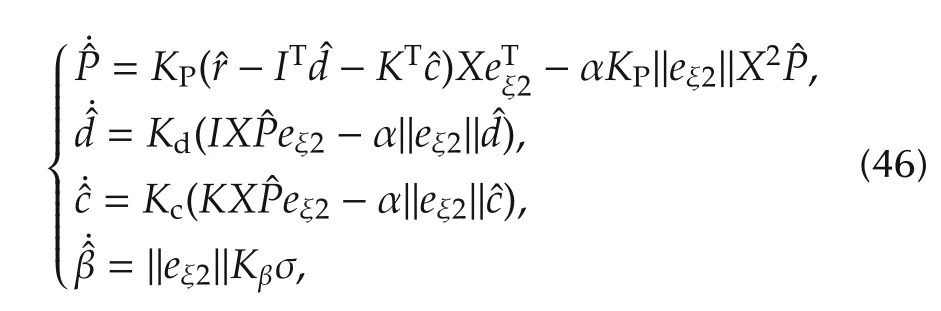
where KP,Kd,Kcand Kβare the positive constant diagonal matrices.

3.2 Constraint force control design

Given a desired nonholonomic constraint force fndor equivalently,a desired multiplier γd.We will design a constraint-force controller so that f tracks fndor equivalently,γ tracks γnd.The desired multiplier γd(t)is assumed to be bounded and uniformly continuous.We define the tracking error vectors eγ1(t)as

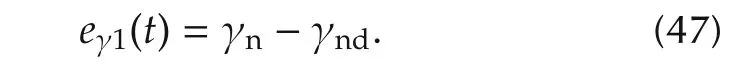
From the definition(47)and(10),we can get

where eγ2= γnd−Kγeγ1,Kγeγ1is the linear proportional derivative type compensator.However,the update-rule forˆη is proposed as

where Kηis the positive constant.

3.3 Stability analysis

Theorem 1 By considering the MMR control system(9),(10),all the Assumptions hold.If the ABFCNC-laws for the tracking-position are(35)and(45),the control law for the constraint force is(49),and the adaptive online learning algorithms for the FCNs and the robust term are designed as(46),and the adaptive robust algorithm for the constraint-force control is designed as(50),then,

1)The parameters of the FCNs and the approximation errors are bounded,and the ABFCNC-state errors eξ1(t),eξ2(t)converge to zero.

2)eγ1(t)and the control inputs are bounded for t≥ 0.The stability of the ABFCNC-system is guaranteed.

Proof 1)Define the Lyapunov function candidate as

By substituting(42)into(52),one can obtain

If the update laws of the ABFCNC system are chosen as(46),then(53)can be rewritten as

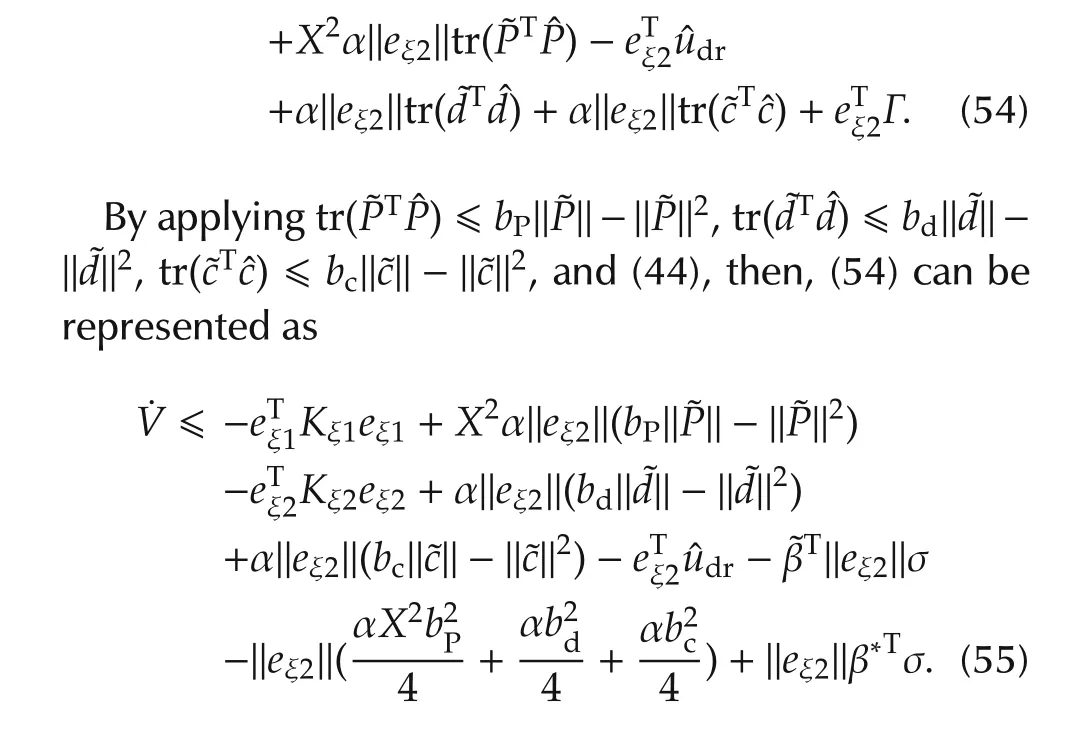
By substituting(45)into(55),it can be concluded that

Accordingto(56),sinceV(eξ1(t),eξ2(t),˜P,˜d,˜c,˜β)≤0and ˙V(eξ1(t),eξ2(t),˜P,˜d,˜c,˜β)is a negative semi-definite function,that is,

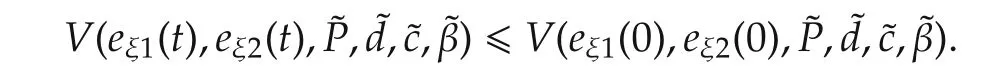
It implies that if eξ1(t),eξ2(t)˜ are bounded at the initial moment t≥ 0,they will remain bounded for t≥ 0.Therefore,eξ1(t),eξ2(t)are bounded for t≥0.Let function Ω(t)≡and integrate the function Ω(t)with respect to time

Since V(eξ1(0),eξ2(0),˜P,˜d,˜c,˜β)is a bounded function and V(eξ1(t),eξ2(t),˜P,˜d,˜c,˜β)is a non-increasing and bounded function,the following resultcan be concluded:

2)By substituting(49)and(50)into(48),we yields

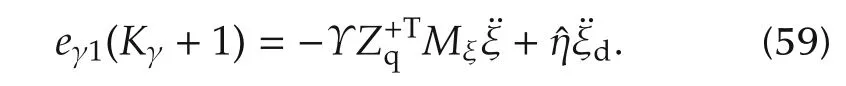
Remark 1 In accordance with the above analyses and the designing of the proposed controllers,the requirement for the bounded uncertainties in our control system is relaxed.The adaptive robust term(45)is used to estimate the bounds of uncertainties,which include the approximation errors,optimal parameter vectors,the parts of Taylor series,and the disturbances of the controlled system.The assumptions for the bounds of parameters are only used to analyze the stability of the control system,and they disappear in our designed controllers.

4 Simulation results

To verify the effectiveness of the proposed method,we consider the 3–DOF mobile manipulator model in[6],as shown in Fig.1.Some parameters of the dynamics of this MMR model are modified as

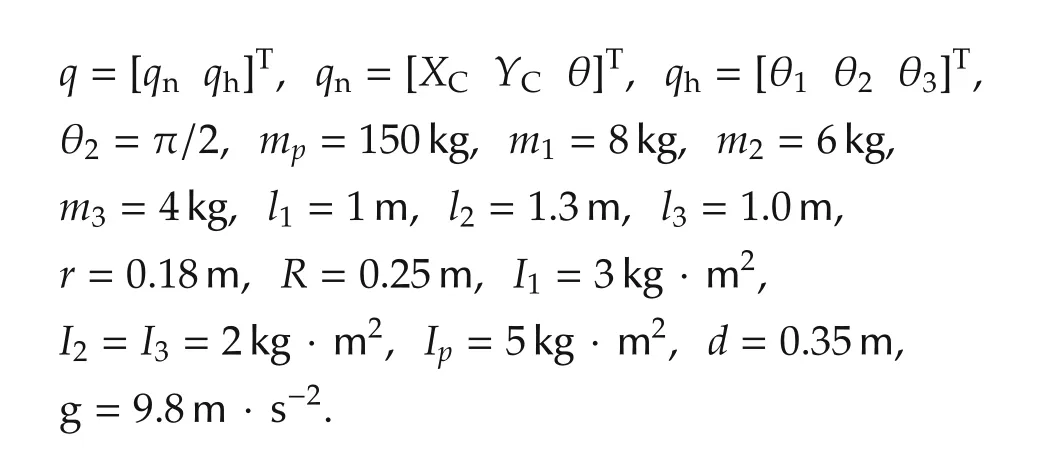
In order to exhibit the superior control performance and effectiveness of the proposed scheme,theproportional-integral-differentialcontrol(PIDC),and the NNs in[9]were examined in the meanwhile.ThePIDC law can be expressed as τ =+portional,integral and differential gain matrices,respec-tively,and they are designed by a compromise between the superiority of control performance and the magnitude of control effort,and they are given as Kpc=diag{90,95,40,40,40},Kic=diag{0.8,0.7,0.4,0.3,0.4},Kdc=diag{1320,1020,850,750,600}.The detailed parameters of the proposed controllers are given as

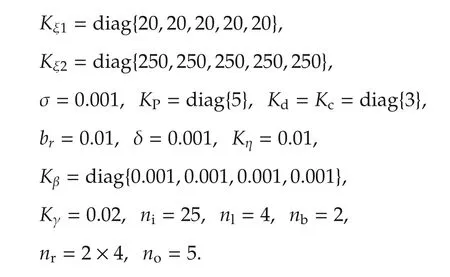
For recording the respective control performances,the mean square error(MSE)of the position-tracking response is define as MSE=where T is the total sampling instants.Based on this definition,the normalized MSE(NMSE)value of the positiontracking response by using a per-unit value with 1 rad is used to examine the control performance.The desired joint positions and nonholonomic-force control of the 3-DOF-mobile-manipulators are defined as ξd=[4t 4.5t sin(2πt/7) π/2 0.5sin(2πt/6)]rad,γd=20.

To investigate the effectiveness and robustness of the proposed scheme,two simulation cases including the parameter variations and disturbances are considered:

The simulated comparisons(the tracking-positions and the tracking-errors)of the PIDC,NNs[10],and ABFCNC schemes are depicted in Fig.4(a)–(c),and(h)–(k)(forCase1)andFig.5(a)–(c),and(h)–(k)(forCase2).Thesimulated-comparisonNMSEvaluesofeachmethod are presented in Tables 1 and 2.In Cases 1 and 2,we can achieve a good tracking-position with the ABFCNC,PIDC,and NNs methods.However,the tracking errors of the proposed ABFCNC strategy converge faster than that of the NNs,and PIDC methods.In addition,we can see in the NMSE measures,the proposed ABFCNC strategy has position tracking improvements than that of the PIDC and NNs schemes.Fig.4(d)–(f)(for Case 1)and Fig.5(d)–(f)(for Case 2)represent the torque-control inputs of the ABFCNC,NNs,and the PIDC methods.In Case 1,the performance of the control-torque inputs of all the methods are good.In Case 2,while the proposed ABFCNC and the NNs strategies can show good torque input performances at the parameter variation conditions(higher-frequency disturbances,changing load on links),then PIDC torque input performance has occurred chattering phenomena.In the simulation of the PIDC scheme,the PID parameters are chosen according to the Ziegler-Nichols tuning rules that based on the step response of robot-control system.However,the MMR-control system is the complex model,so,the selection of the PIDC parameters is not easy.The performance of the PIDC,shown in the simulation results,are the best in terms of handling the heuristic process,but the chattering phenomena still exists when the frequency of the external disturbances increases or the load of the robot system is changed suddenly.In the NNs[10]simulation,some control parameters,such as RBF function parameters that help achieving highaccuracy are not easy to determine.These drawbacks cause the adaptation of the controllers-based NNs,or the PIDCs are lower than in the proposed method.In the proposed method simulation,the parameters of the proposed controller are chosen through some trials.The rise-time of the steady-state-error can be reduced by increasing Kξ1,Kξ2,Kγ.However,the fast rise-time and small steady-state-error will increase the control input.The learning parameters α,KP,Kd,Kc,Kη,Kβare chosen based on the response of the tuning objects and the accuracy of the approximation process.The selection of these parameters relates to the convergence rate of the state error.High learning rates may cause the ABFCNC system produces unstable output although the convergence speed becomes faster.

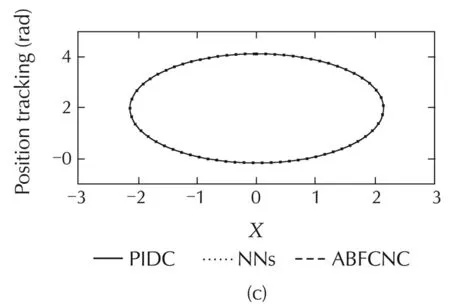
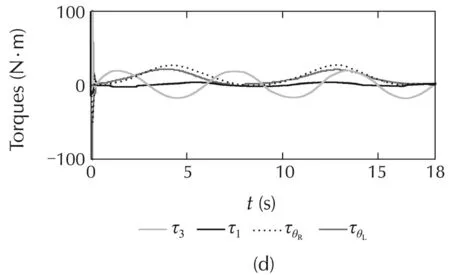
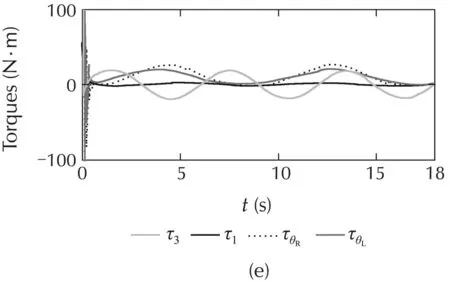
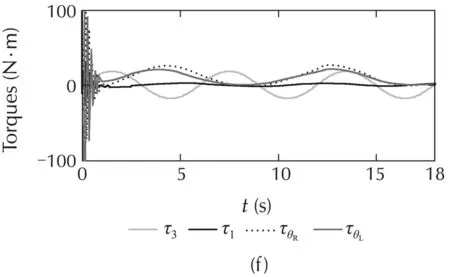
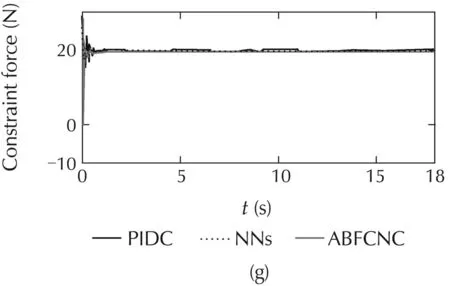
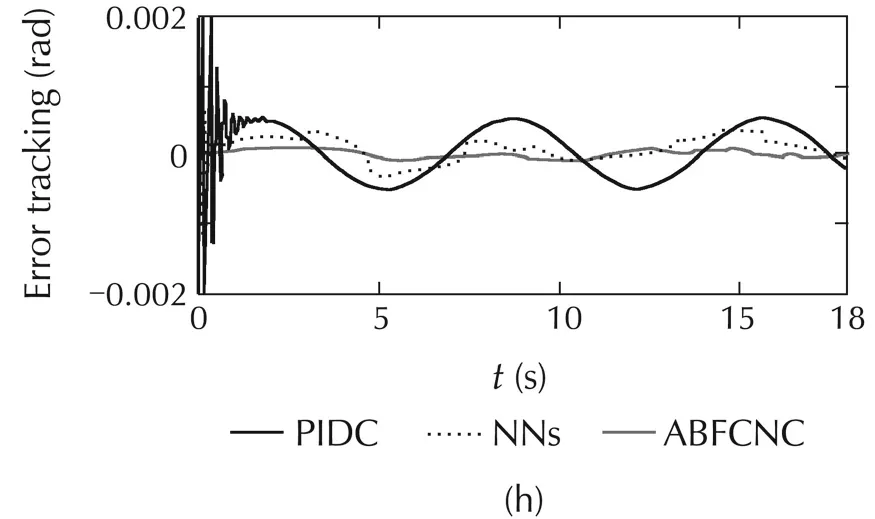
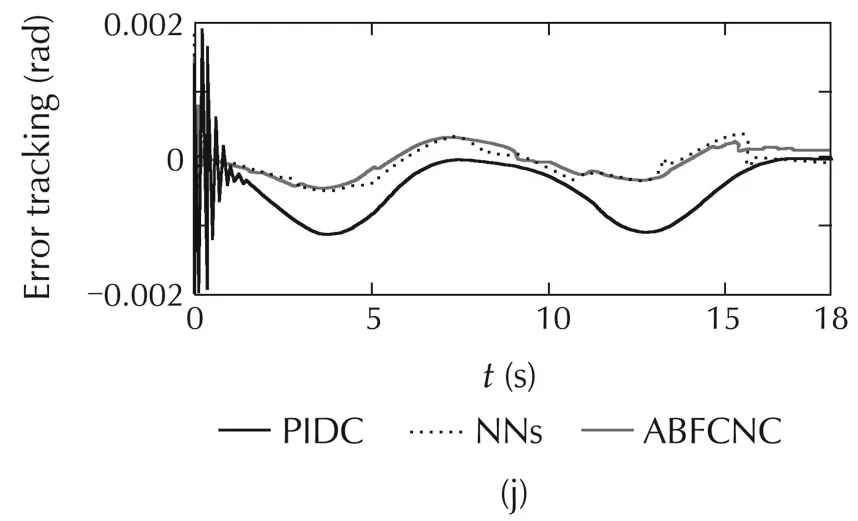
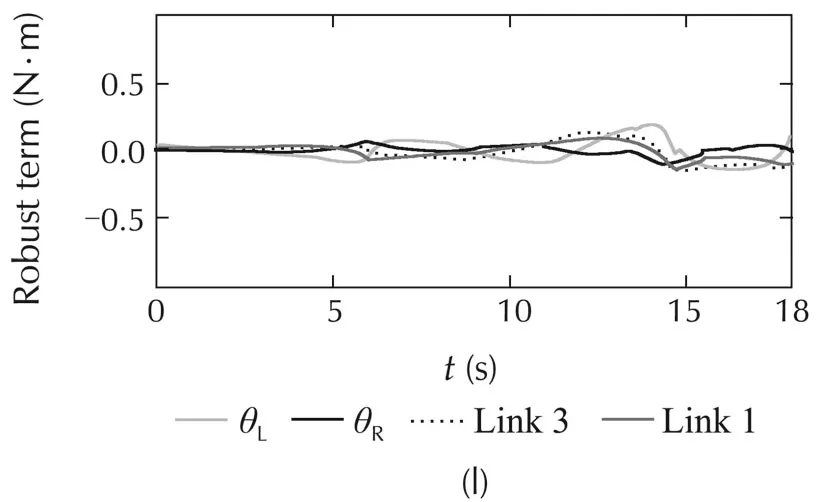
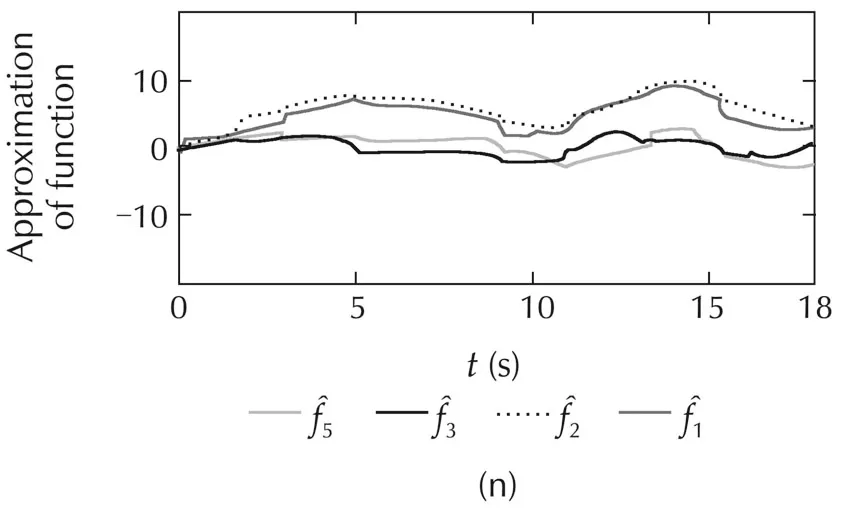
Fig.4 Simulation results with Case 1.(a)Link 1,(b)Link 3,(c)mobile base,(d)ABFCNC,(e)NNs,(f)PIDC,(h)Link 1,(i)Link 3,(j)θL,and(k)θR.

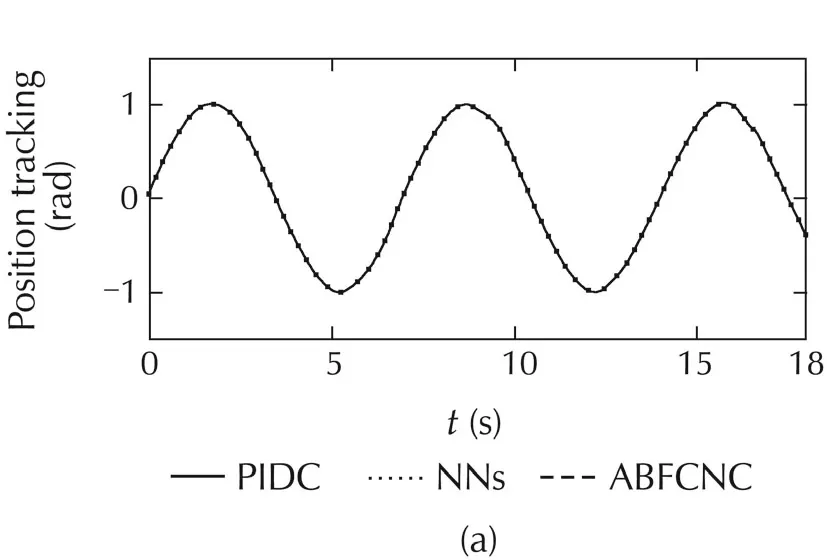
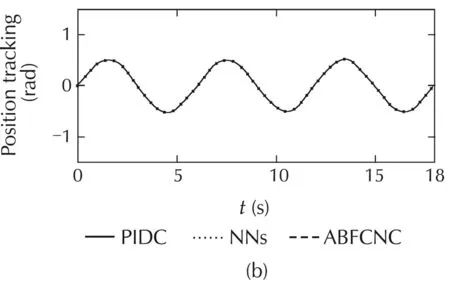
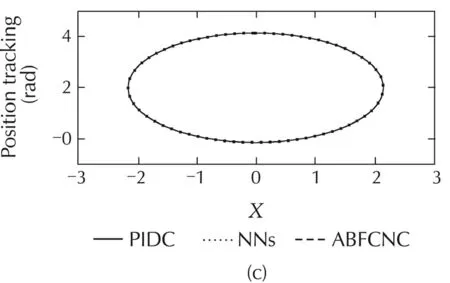
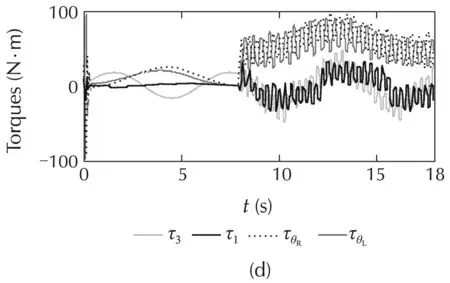
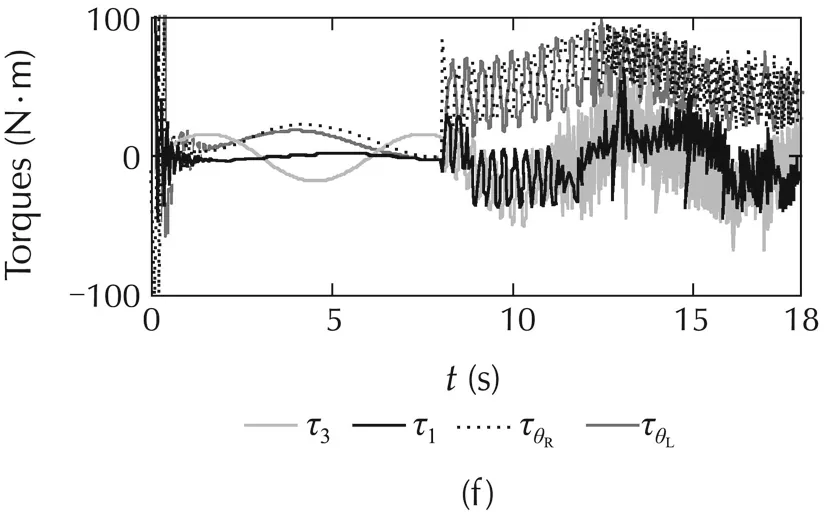
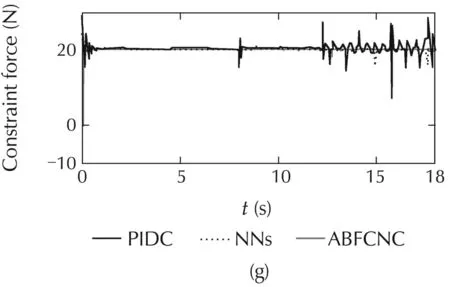
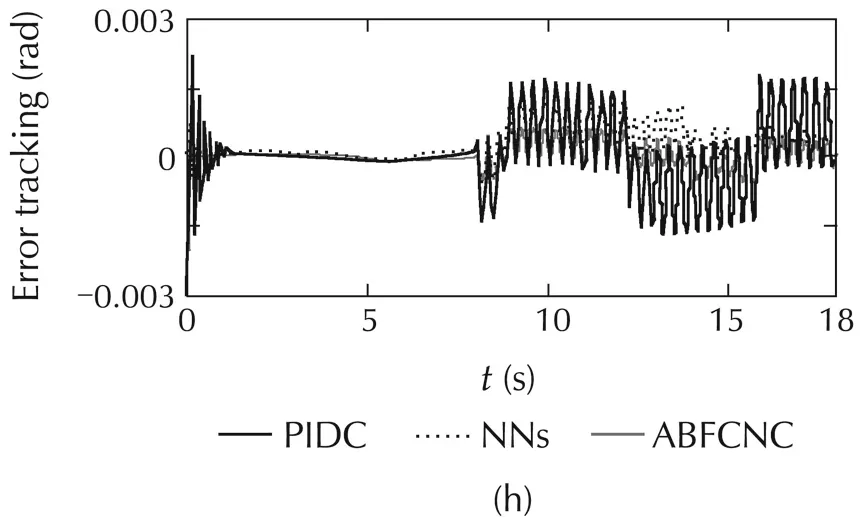
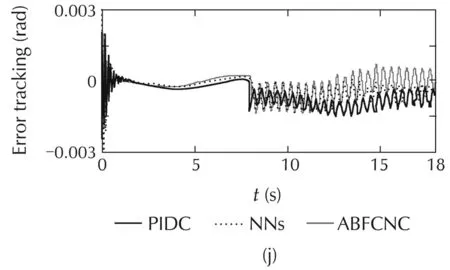
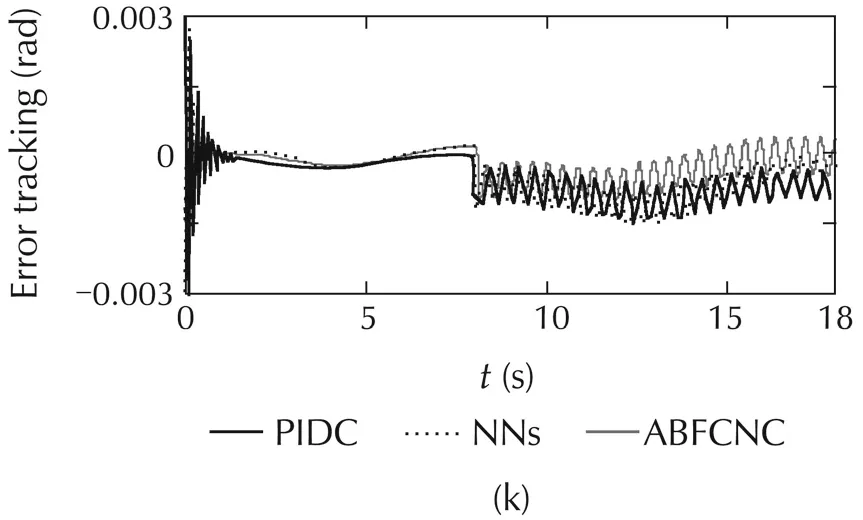
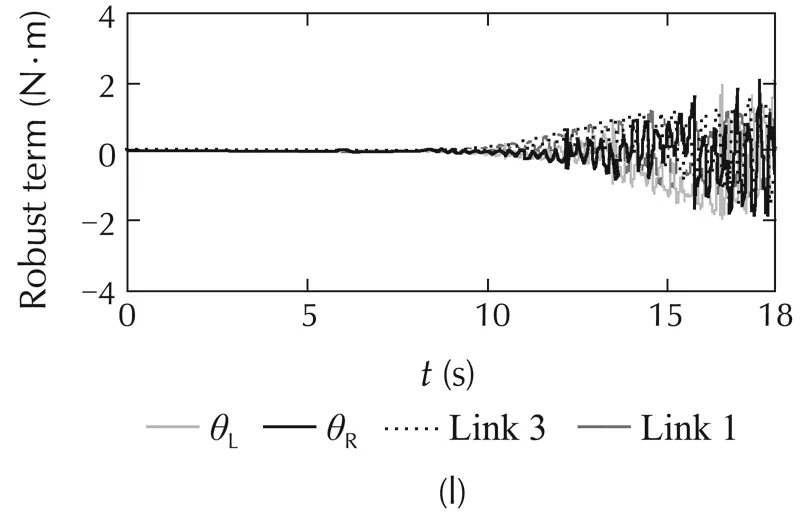
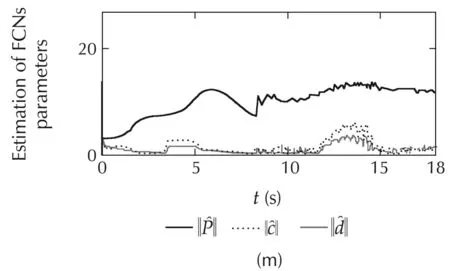
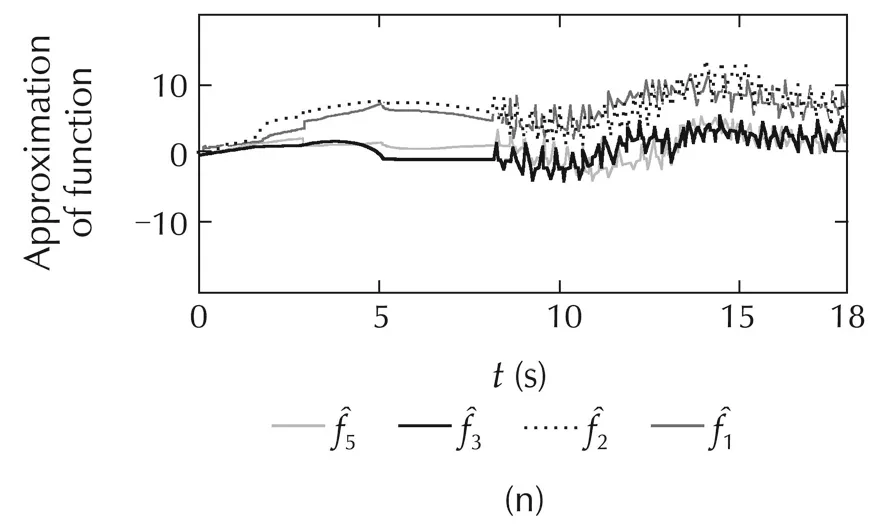
Fig.5 Simulation results with Case 2.(a)Link 1,(b)Link 3,(c)mobile base,(d)ABFCNC,(e)NNs,(f)PIDC,(h)Link 1,(i)Link 3,(j)θL,and(k)θR.

The simulated comparisons with the constraint-force of all the methods are represented in Fig.4(g),and Fig.5(g).The constraint-force designing of the NNs controller is similarto ABFCNC controller.However,the constraint-force designing of PIDC scheme is different,and the PIDC for the constraint-force is considered.In Case1,theperformanceofconstraint-forceoftheABFC-NC and NNs methods is good,but the simulation result of the PIDC is poor in the steady state.In Case 2,while the proposed method can show good constraint-force performance at the parameter variation conditions,and then,the simulation results of the NNs and PIDC are not good,and undesired response appears when time increases.Here,the robust characteristic of the proposed controller can be set with regard to the parameter variation and external disturbances.The simulated results of the robust term,FCNs outputs and estimation parametersoftheproposedcontrolsystem(withrespecttoCases 1 and 2)are depicted in Fig.4(l)–(n)and Fig.5(l)–(n).These simulation results are good,and they have proved the correctness of the proposed method including the boundedness of the control system parameters.Based on the comparison simulations,the proposed ABFCNC method is more suitable to be implemented to control the mobile-manipulator robot under the occurrence of parameter variation and external disturbances.

Table 1 NMSE comparisons of ABFCNC,NNs and PIDC schemes with Case 1(unit:×104rad).

Table 2 NMSE-comparisons of ABFCNC,NNs and PIDC schemes with Case 2(unit:×104rad).

5 Conclusions

In this paper,we presented a novel ABFCNC strategy for motion/force of the MMR.The FCNs have been applied in the tracking-position ABFCNC system to approximate the dynamics of the robotic control system.The proposed control system has guaranteed the requirement for high accuracy of the position-tracking errors and nonholonomic constraint force under variation conditions.In the ABFCNC system,the information about constrained/assumption conditions or dynamics,and uncertainties of robotic system control is not required.In addition,all adaptive online learning laws in the proposed control system are obtained in the sense of Lyapunov stability theorem so that the stability of the closed-loop control system can be guaranteed whether or not the appearance of uncertainties According to the comparison results of the simulation process,besides the stability and robustness features,the performance of the ABFCNC system has been improved.The proposed method can be applied as a good alternative in the existing MMR control system.

[1]Y.Yamamoto,X.Yun.Effectofdynamicinteraction on coordinated control of mobile manipulators.IEEE Transactions on Robotics and Automation,1996,12(5):816–824.

[2]K.Watanabe,K.Sato,K.Izumi,et al.Analysis and control for an omnidirectional mobile manipulator.Journal of Intelligent and Robot Systems,2000,27(1/2):3–20.

[3]F.Inoue,T.Murakami,K.Ohnishi.A motion control of mobile manipulator with external force.IEEE/ASME Transactions on Mechatronics,2002,6(2):137–142.

[4]W.Dong.On trajectory and force tracking control of constrained mobile manipulators with uncertainty.Automatica,2001,38(9):1475–1484.

[5]Z.Li,S.S.Ge,A.Ming.Adaptive robust motion/force control of holonomic-constrained nonholonomic mobile manipulators.IEEE Transactions on Systems,Man,and Cybernetics–Part B:Cybernetics,2007,37(3):607–616.

[6]Z.Li,S.S.Ge,M.Adams,et al.Robust adaptive control of uncertain force/motion constrained nonholonomic mobile manipulators.Automatica,2008,44(3):776–784.

[7]Z.Li,Y.Yang,J.Li.Adaptive motion/force control of mobile under actuated manipulators with dynamics uncertainties by dynamic coupling and output feedback.IEEE Transactions on Control Systems Technology,2010,18(5):1068–1079.

[8]F.L.Lewis,S.Jagannathan,A.Yesildirek.Neural Network Control ofRobotManipulatorsandNonlinearSystem.Philadelphia:Taylor&Francis,1999.

[9]F.L.Lewis,A.Yesildirek,K.Liu.Multilayerneural-net robot controller with guaranteed tracking performance.IEEE Transactions on Neural Networks,1996,7(2):388–399.

[10]S.Lin,A.A.Goldenberg.Neural-network control of mobile manipulators.IEEETransactionsonNeuralNetworks,2001,12(5):1121–1133.

[11]C.Lee,T.Eom,J.Lee.Neuro-adaptive control of mobile manipulators base on compensation of approximation error.IET Electronics Letters,2002,38(16):935–936.

[12]D.Xu,D.Zhao,J.Yi,et al.Trajectory tracking control of omnidirectional wheeled mobile manipulators:robust neural network-based sliding mode approach.IEEE Transactions on Systems,Man,and Cybernetics–Part B:Cybernetics,2009,39(3):1653–1658.

[13]J.B.Mbede,P.Ele,C.M.M.Abia,et al.Intelligent mobile manipulator navigation using adaptive neuro-fuzzy systems.Information sciences,2005,171(4):447–474.

[14]J.S.Albus.A new approach to manipulator control:the cerebellar model articulation controller(CMAC).Journal of Dynamic Systems,Measurement,and Control,1975,97(3):220–227.

[15]Y.H.Kim,F.L.Lewis.Optimal design of CMAC neural-network controller for robot manipulators.IEEE Transactions on Systems,Man,and Cybernetics–Part C:Applications and Reviews,2000,30(1):22–31.

[16]C.Lin,Y.Peng.Adaptive CMAC-based supervisory control for uncertain nonlinear systems.IEEE Transactions on Systems,Man,and Cybernetics–Part B:Cybernetics,2004,34(2):1248–1260.

[17]S.Su,Z.J.Lee,Y.Wang.Robust and fast learning for fuzzy cerebellar model articulation controllers.IEEE Transactions on Systems,Man,and Cybernetics–Part B:Cybernetics,2006,36(1):203–208.

[18]W.Yu,F.O.Rodriguez,M.A.M.Armendariz.Hierarchical fuzzy CMAC for nonlinear systems modeling.IEEE Transactions on Fuzzy Systems,2008,16(5):1302–1314.

[19]C.Lin,H.Li.A novel adaptive wavelet fuzzy cerebellar model articulation control system design for voice coil motors.IEEE Transactions on Industrial Electronics,2012,59(4):2024–2033.

[20]M.Krstic,I.Kanellakopoulos,P.V.Kokotovic.Nonlinear and Adaptive Control Design.New York:Wiley,1995.

[21]C.C.Tsai,M.Cheng,S.Lin.Dynamic modeling and tracking controlofanonholonomicwheeledmobilemanipulatorwithdual arms.Journal of Intelligent and Robotic Systems,2006,47(4):317–340.

[22]F.Hong,S.S.Ge,C.Pang,et al.Robust adaptive neuro-fuzzy control of uncertain nonholonomic system.Journal of Control Theory and Applications,2010,8(2):125–138.

[23]S.Tong,Y.Li.Adaptive fuzzy output feedback tracking backstepping control of strict-feedback nonlinear systems with unknown dead zones.IEEE Transactions on Fuzzy Systems,2012,20(1):168–180.

[24]S.Chen,W.Ho,J.Chou.Robust controllability of T-S fuzzymodel-based control systems using sliding-mode technology.IEEE Transactions on Fuzzy Systems,2009,17(6):1324–1335.

[25]Z.Xi,G.Feng,T.Hesketh.Piecewise sliding-mode control for T-S fuzzy system.IEEE Transactions on Fuzzy Systems,2011,19(4):707–716.

[26]J.J.E.Slotine,W.Li.Applied Nonlinear Control.Englewood Cliffs:Prentice-Hall,1991.

Thang-Long MAI received the B.Sc.and M.Sc.degrees from Department of Automatic Control,Faculty of Electrical and Electronics,Viet Nam National University,Ho Chi Minh City University of Technology.He received the Ph.D.degree at College of Electrical and Information,Hunan University,China.His current research interests include robotic control,learning control and intelligent control.E-mail:mailongtk@gmail.com.

Yaonan WANG received the B.Sc.degree in Computer Engineering from East China Science and Technology University(ECSTU),Fuzhou,China,in1981,andtheM.Sc.and Ph.D.degrees in Electrical Engineering from Hunan University,Changsha,China,in 1989 and 1995,respectively.From 1995 to 1997,he was a postdoctoral research fellow with the National University of Defense Technology.From 1981 to 1994,he worked with ECSTU.From 1998 to 2000,he was a senior Humboldt fellow in Germany,and from 2001 to 2004,he was a visiting professor with the University of Bremen,Bremen,Germany.He has been a professor at Hunan University since 1995.His research interests are intelligent control and information processing,robot control,image processing,and industrial process contro.E-mail:yaonan@hnu.cn.

Journal title change

We would like to inform you that the title of‘Journal of Control Theory and Applications’is changed to ‘Control Theory and Technology’.The change will be effective from the beginning of 2014.

We welcome your submissions for the journal with new title(http://controls.papercept.net).

2 May 2014;revised 14 November 2014;accepted 17 November 2014

†Corresponding author.

E-mail:mailongtk@gmail.com.Tel.:+84 902 698 315.

This work was supported by the National Natural Science Foundation of China(Nos.6117075,60835004)and the National High Technology Research and Development Program of China(863 Program)(Nos.2012AA111004,2012AA112312).

©2014 South China University of Technology,Academy of Mathematics and Systems Science,CAS,and Springer-Verlag Berlin Heidelberg