GPU加速的图像实时分形编码

孙 冬，高清维，卢一相，竺 德

(安徽大学电气工程与自动化学院，安徽合肥 230601)

作为新一代的图像压缩技术，分形编码自20世纪80年代提出以来，由于具有极高的压缩比和较好的解码质量，引起了人们的广泛关注.然而分形编码时间过长是其固有的缺点，这也限制了它的推广和应用.为减少编码时间，近30年来许多学者对此开展了深入研究［1－3］，他们的工作主要集中于:如何在不明显降低图像解码质量的基础上，尽可能地减少待搜索父块的数量.在已经提出的诸多改进方案中，以Davids的工作最为出色，他提出的小波域分形(wavelet－fractal，简称FW)编码算法［1］能够极大地缩短编码时间，而且解码图像质量更高.虽然后人对FW编码方案又进行了许多改进，但编码时间距实时化仍有约2个数量级的差距.

现代处理器的架构已经将并行计算作为提高性能的一个最重要途径.高性能的CPU由于很难克服提高时钟频率后的散热问题，转而使用增加运算核心的方法来加速.作为CPU的协处理器，图形处理器(graphics processor unit，简称GPU)的计算能力在近年内以远超摩尔定律的速度爆炸性增长.据报道2013年nVidia公司基于开普勒架构GK110核心的GTX Titan型GPU单精度浮点运算峰值速度达每秒4.5万亿次，拥有2 688个流处理单元，由71亿个晶体管组成，而热设计功耗仅为250 W.由于GPU拥有CPU所不具有的超密集高并行的计算特点，将GPU用于非图形领域的通用科学计算逐渐成为人们关注的热点，具有重要的理论意义和应用价值［4－7］.受此启发，作者将GPU应用到图像分形编码中，以寻求一种高实时性的编码方案.

1 FW编码原理

Barnsley认为，自然界的图像具有局部自相似性［8］.Jacqain根据这一假设，把图像描述成一个带灰度映射的局部迭代函数系统(local iterated function system with gray level maps，简称LIFSM)的吸引子.文献［9－10］中给出了LIFSM的编码原理，将图像分割成若干不重叠的块，并为每个块寻找一个与其相似的父块及对应的映射关系.

由于空域中大小为2J×2J的块交流成分在小波域中近似地对应为根在第J级子带上的小波树SJ，因此，当空域中的两个块具有相似性时，它们在小波域中所对应树的各级数据之间也具有相似性，并且这种相似性是一致的(空域块的自相似性和相应小波域中树的自相似性请参见图1，图1b中，每棵树由3个方向的分支组成).Davis根据这一事实，把LIFSM编码引入小波域，提出了FW编码算法，将空域中块的相似性用小波域中树的相似性来近似等价.与LIFSM编码相比，FW编码算法能够极大地缩短编码时间，而且解码图像的视觉质量也更高.

图1 自相似性Fig.1 Self-similarity

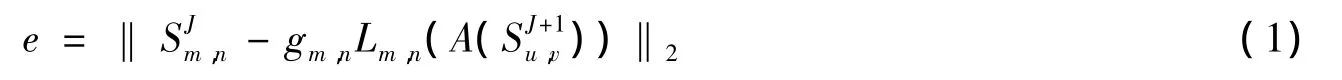
gm，n为对比度变换因子，定义为

其中:Cov为协方差运算.

因为FW编码是有损的，所以为了能够在编码时对图像质量进行控制，可以对(1)式中的误差e设定上限阈值E，并且规定当e＞E时，不再对树进行FW码的近似存储，而是直接储其小波系数.显然，当E充分大时，FW编码将退化为小波编码，但是编码时间不会减少，因为最优父树的搜索是必需的.

FW的解码是逐级迭代完成的.因为根在第J+1级子带(u，v)处的父树与根在第J级子带(m，n)处的子树具有相似性，因此可以使用下式从父树中恢复子树数据

J次迭代后，解码完成.

2 并行化算法

计算统一设备架构(compute unified device architecture，简称CUDA)是通用GPU计算的一种技术规范，由NVidia公司于2007年提出.与传统的通用GPU计算方式不同，在CUDA规范下，用户可以用C或其他语言进行自由的GPU编程，而不再需要调用图形API.CUDA程序由在CPU上执行的Host部分和在GPU上执行的Device部分共同组成，其中，Host部分主要负责Host端资源(内存)的分配与释放、Device端资源(全局显存、纹理显存、共享显存、寄存器)的分配与释放、内存与显存之间数据的I/O;Device部分主要负责显存中数据的计算、计算线程的同步.在Device中执行的代码称为内核(Kernal).基于CUDA的GPU编程模型如图2所示.

图2 基于CUDA的GPU编程模型Fig.2 The GPU programming model based on CUDA

从图2可知，Device部分数据并行处理在逻辑上是由众多的线程(Thread)共同完成的，这些线程将各自处理显存中数据的一小部分.CUDA中的线程是分级组织的:多个线程可以组成一个块(Block)，多个块又可以组成一个网格(Grid).一般情况下，一个网格就代表一个计算任务.因为网格和块可以在程序中定义成一维或多维(网格最多可定义为二维，块最多可定义为三维)，所以在实际编程中，可根据需要对计算任务进行自由的切割以方便程序的编写.

由FW编码原理可知，对图像进行编码的实质是为每棵根在第J级子带处的子树搜索一棵与其最为相似的父树.为了加速这一过程，可以使用并行的方法，为所有的子树同时进行最优父树搜索.根据CUDA编程模型，作者提出的并行化的FW编码算法如图3所示.

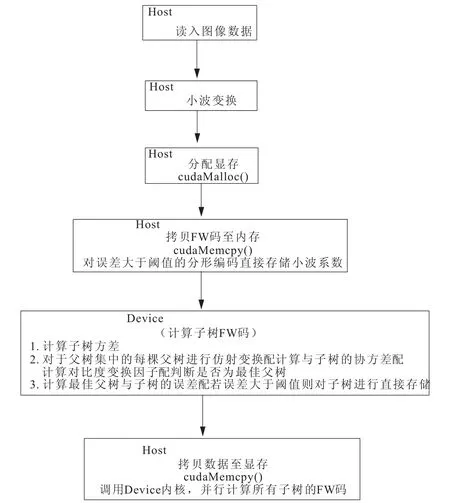
图3 并行FW编码算法Fig.3 The parallelized version of FW encoding algorithm

在图3中，每个子树的编码过程都由一个Device线程进行处理.因为每个GPU核心只能同时运行一个线程，所以GPU核心数量N越大，线程运行的并发性就越好，总的编码速度也就越快.可以证明，若一个算法中有P部分(0≤P≤1)可以做并行处理时，理想情况下的加速比为

在FW编码中，因为小波变换部分的计算量远小于编码部分，所以P≈1，此时加速比可接近最大值N.考虑到当今的主流GPU都具有数量众多的核心，所以当使用GPU代替CPU进行编码时，性能会有本质上的提升.

3 实验

为验证该文算法的正确性和有效性，使用一幅512×512的标准测试图像“Lena”，分别用CPU和GPU对其进行FW编码和解码，并对解码图像和编码时间进行对比.其中FW编码算法中的小波变换部分采用“sym4”小波，作4级变换，分形编码部分误差阈值E=200.程序开发环境为Visual C++2005，软件运行环境为32位Windows 7，内存为4 GB.

图4给出了分别使用CPU和GPU对测试图像进行编码后的解码图像(50%的比例显示)，其中PSNR=32.69.

图4 FW解码图像Fig.4 FW decoded images

由图4可知，采用GPU的解码图像和CPU的解码图像是一致的，这证明了GPU编码的正确性.表1给出了不同规格GPU对测试图像进行编码的时间，并与CPU的编码时间进行对比.其中编码时间的计算从小波变换之后开始到FW码由显存拷贝回内存后结束，运行10次取最小值;CPU的计算时间为仅使用1颗核心时的结果.

表1 GPU与CPU的FW编码时间对比Tab.1 The comparison of FW encoding time between GPU and CPU

由表1可见，采用GPU的编码时间远小于CPU的编码时间，因此采用GPU进行FW编码是快速有效的，且具有较高的实时性.

4 结束语

借助于GPU强大的计算能力，作者所提出的并行FW编码方案可以在不降低图像质量的情况下，大幅减少编码所需的时间，实现了图像分形编码的实时化，具有重要的实用价值.

［1］Davis G.A wavelet－based analysis of fractal image compression［J］.IEEE Trans on Image Processing，1998，7(2):141－154.

［2］Hyun J，Lickho S.A spectrum－based searching technique for the most favorable section of digital music［J］.IEEE Trans Consumer Electronics，2009，55(4):2122－2126.

［3］Lv J，Ye Z X，Zou Y R.Huber fractal image coding based on a fitting plane［J］.IEEE Trans on Image Processing，2013，22(1):134－145.

［4］冯娜.基于GPU的档案数据库应用研究［J］.武汉理工大学学报，2011，33(6):148－151.

［5］Chen Y W.Fast virus signature matching based on the high performance computing of GPU［C］∥IEEE International Conference on Communication Software and Networks，2010:513－515.

［6］杨正龙，金林，李蔚清.基于GPU的图形电磁计算加速算法［J］.电子学报，2007，35(6):1056－1060.

［7］马巍巍，孙冬，吴先良.基于GPU的高阶辛FDTD算法的并行仿真研究［J］.合肥工业大学学报:自然科学版，2012，35(7):926－929.

［8］Barnsley M F，Sloan A D.A better way to compress images byte［M］.McGraw－Hill:Inc Hightstown NJ USA，1988:215－223.

［9］Jacqain A E.A novel frctal block－coding technique for digital image［C］∥IEEE International Conference on Acoustics，Speech，and Signal Processing，1990:2225－2228.

［10］Wohlberg B，Jager B D.A review of the fractal image coding literature［J］.IEEE Trans on Image Processing，1999，8(12):1716－1729.

［11］赵健，雷蕾，蒲小勤.分形理论及其在信号处理中的应用［M］.北京:清华大学出版社，2008:57－75.