Xe、Ba和Ce同位素偶偶核形变演化研究

黄 海，郭建友

(1.安徽大学 物理与材料科学学院，安徽 合肥 230039;2.安徽医科大学生命科学学院，安徽 合肥 20032)

形状演化和相变是原子核理论和实验研究的热点之一［1］.实验方面，陆续发现了形状演化的关键点核，如具有X(5)和E(5)对称的原子核［2］.特别需要指出的是:实验上发现稳定的八极形变存在于锕系区 Ra～Th(Z=88，N=136)和镧系区 Ba～Sm(Z=56，N=88)附近的原子核当中［2］，如在252Cf由于自发裂变产生的γ光谱分析中，Phillips等指出144Ba和146Ba呈现明显的八极形变［3］，同样的现象也在148Nd、150Sm 和146～150Ce 核中被发现［4］.八极形变的发现，使原子核的形状演化和相变研究受到更加广泛的关注.理论方面，相对论微观自洽计算的HFB(Hartree－Fock－Bogoliubov)方法常被用于原子核形状演化和相变研究.近年来，相对论平均场理论［5－10］(relativistic mean field，简称为RMF)在描述原子核形变和相变领域中取得了一系列进展［11－14］.文献［15］通过引入反射不对称自由度参数，在平均场模型中采用双中心谐振子(TCHO)势［16－17］本征函数作为基展开Dirac旋量的方法，将RMF理论进一步发展为能反映原子核八极形变的反射不对称相对论平均场理论(RAS－RMF).文献［18－19］利用RAS－RMF模型，分别计算分析了Sm及Th同位素链的形状演化及位能曲线，研究表明在Sm及Th同位素链中具有X(5)对称性的形状相变点分别是152Sm及224Th核.作者利用RAS－RMF理论模型，深入探讨并研究了八极形变对Xe、Ba和Ce同位素偶偶核基态性质的影响，理论计算结果能清晰地展现Xe、Ba和Ce同位素偶偶核形状演化的规律.

1 理论框架

在相对论平均场(RMF)模型中，运动在介子场中的核子被视为Dirac粒子，依靠交换光子和介子传递核子之间的相互作用，其拉格朗日量为

其中:ψ为质量为M核子的Dirac旋量;ρ为矢量－矢量介子;ω为提供短程排斥力的标量－矢量介子;σ为提供中程吸引的标量－标量介子;A为光子场，描述原子核的电磁属性.

利用变分原理，可得到核子运动的Dirac方程

和介子的Klein－Gordon方程

严格求解非线性方程(2)和(3)是十分困难的，通常采用双中心谐振子(TCHO)势的本征函数作为基展开Dirac旋量和，同时在RMF计算中引入反射不对称自由度(RAS－RMF)的方法来近似求解方程(2)和(3).

在RAS－RMF理论模型中，Dirac旋量ψi形式为

双中心谐振子势为

其中:M为核子质量;ω1(ω2)分别表示z＜0(z≥0)情况下的谐振子振荡频率;z1及z2分别表示2个椭球体的中心到它们相交平面的垂直距离.在此表示形式下，可由以下3个参数完全确定双中心谐振子势:第1个参数是描述双中心谐振子基中心之间的距离Δz(Δz=z1+z2);第2个参数为四极形变参数δ2;第3个参数是反射不对称自由度参数δ3.

2 计算及其结果讨论

在利用RAS－RMF计算的过程中，对关联采用固定能隙的BCS近似处理，对能隙MeV，选取一组最佳双中心谐振子基的参数(不对称自由度 δ3=0.99、形变 δ2=0.20、大小 N=17)［20］，相互作用取广泛使用的PK1［21］参数组.以质子数Z=56为中心，选取了Xe、Ba和Ce核，计算并比较分析了它们同位素偶偶核的核子结合能、形变参数及物质密度分布.

表1为由RAS－RMF计算得到的核子结合能与其实验值［22］的比较.对比表1数据可以看出:RAS－RMF理论计算结果与已知的实验数据相符合.在质量数A较小范围内，随着质量数的增加，Xe、Ba和Ce核子结合能逐渐递增;138Ba和140Ce核子结合能最大时，对应的中子数N均为满壳数82，原子核状态最稳定;随着中子数N继续增大，核子结合能又逐步减小，即原子核稳定性逐步变弱.

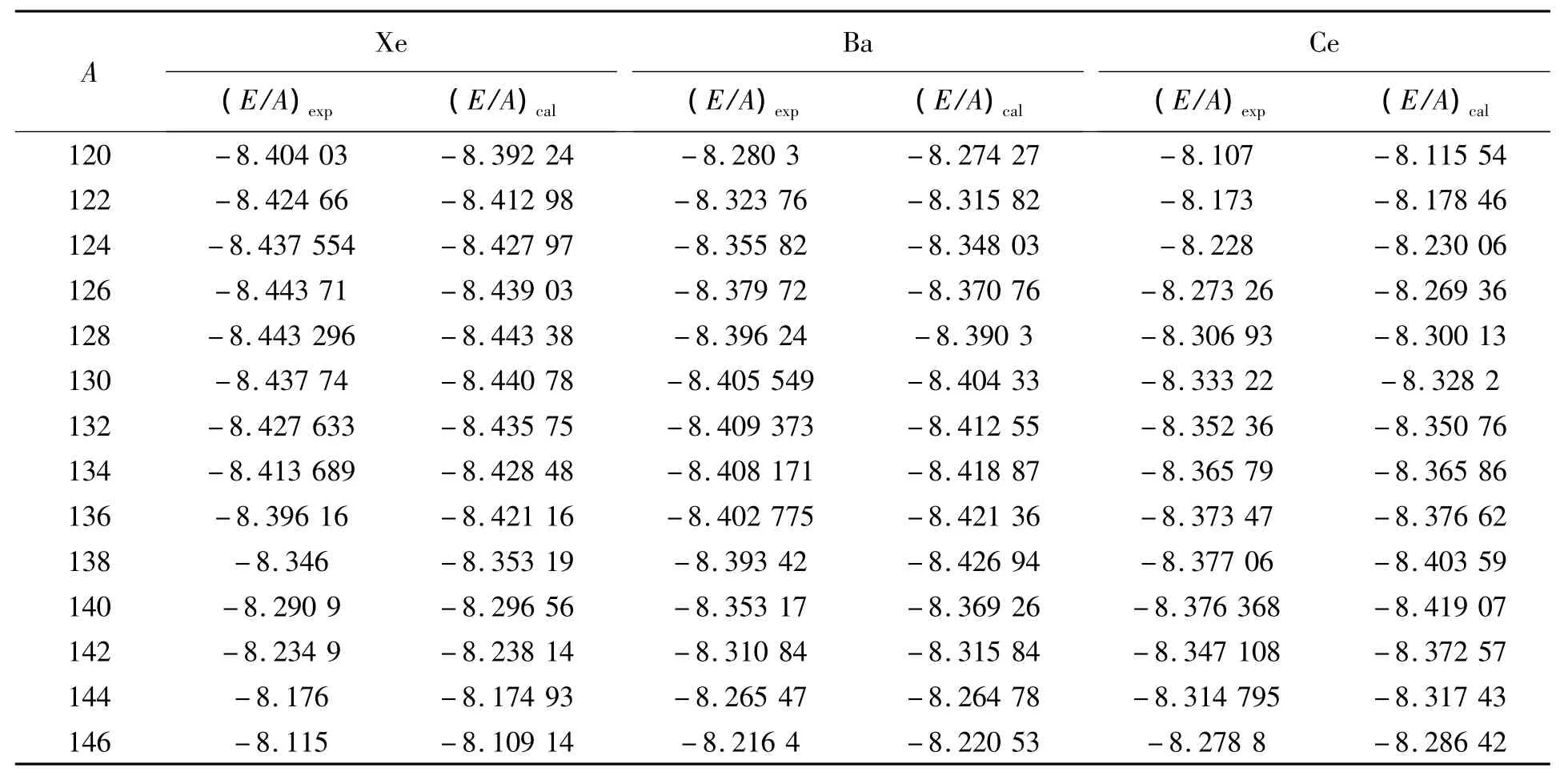
表1 由RAS－RMF计算得到的核子结合能与其实验值的比较Tab.1 The comparison between the experimental values and the calculated nuclear binding energies by RAS-RMF MeV

原子核的形状演化规律主要由四极形变决定，同时八极形变的出现也会影响到原子核形状演化及相变.通过引入反射不对称自由度，RAS－RMF理论计算不仅获得了原子核的四极形变参数β2，同时获得了八极形变参数β3.图1、2分别展示了Xe、Ba和Ce同位素偶偶核质量数A变化时，其四极形变参数β2与八极形变参数β3随之变化的规律.在图1中，圆圈(○)代表RAS－RMF计算获得的四极形变数值，方框(□)代表实验值［23］.从图1可以看出，RAS－RMF模型计算结果与已知的实验值基本吻合，原子核的四极形变参数β2随质量数A变大均呈现先减小后增大的变化规律.当质量数A较小时，如120－134Xe、120－132Ba和120－134Ce，四极形变参数 β2均较大，原子核为轴对称长椭球形四极形变核;当质量数A增大时，如136－140Xe、136－142Ba和136－144Ce，四极形变参数 β2值迅速减小为零，原子核形状由轴对称长椭球形四极形变核向近球形演化.当质量数A再继续增大时，Xe、Ba和Ce的四极形变参数β2又逐渐变大，原子核又为轴对称长椭球形四极形变核.由图2可以看出，Xe、Ba、Ce同位素偶偶核只在一些特定较小质量数A范围内，如108－118Xe、144－156Ba和148－156Ce，有较为明显的八极形变出现，而其余的同位素偶偶核均无八极形变，这与理论预言镧系区Ba～Sm(Z=56，N=88)附近，原子核有比较稳定的八极形变相吻合，且与实验上观测到的八极形变不稳定现象相一致.综合四极形变参数β2和八极形变参数β3变化的规律，可知Xe、Ba和Ce同位素偶偶核均有四极形变与八极形变共存现象(八极形变β3的数值相比于四极形变β2的数值要小得多)，并且随着质量数A的增大，八极形变β3逐渐减小，而四极形变β2逐渐增大，表明原子核八极形变较弱，逐渐向四极形变转化.

图1 Xe、Ba和Ce同位素偶偶核的四极形变随质量数变化的规律Fig.1 Quadrupole deformation for the even－even Xe，Ba and Ce isotopes as functions of mass number

图2 Xe、Ba和Ce同位素偶偶核的八极形变随质量数变化的规律Fig.2 Octupole deformation for the even－even Xe，Ba and Ce isotopes as functions of mass number

为了更直观地展示并比较Xe、Ba和Ce同位素偶偶核形状演化规律，分别给出了Xe、Ba和Ce同位素偶偶核在x=0平面的物质密度分布图，如图3所示.对Xe同位素偶偶核，如图3a，当质量数A=106时，原子核为轴对称椭球形四极形变核，随着质量数的增大，当A=110时，原子核出现明显的八极形变，为不对称的梨形，随质量数的进一步增加，八极形变变弱，四极形变增强，原子核又呈现轴对称长椭球形.相同的情况也出现在Ba和Ce同位素偶偶核形状演化规律之中，如图3b、c所示.分析可知:Xe、Ba和Ce同位素偶偶核都有八极形变出现的质量数A取值范围(对Xe核，A为108～112;对Ba核，A为144～154;对Xe核，A为146～154)，在此范围内，原子核处于四极形变与八极形变共存状态，形状均呈不对称的梨形，由于四极形变相对于八极形变要强，且八极形变不稳定，原子核又转呈轴对称长椭球形，这一直观的形状演化规律亦与图1、2给出的四极形变β2和八极形变β3的变化规律相一致.

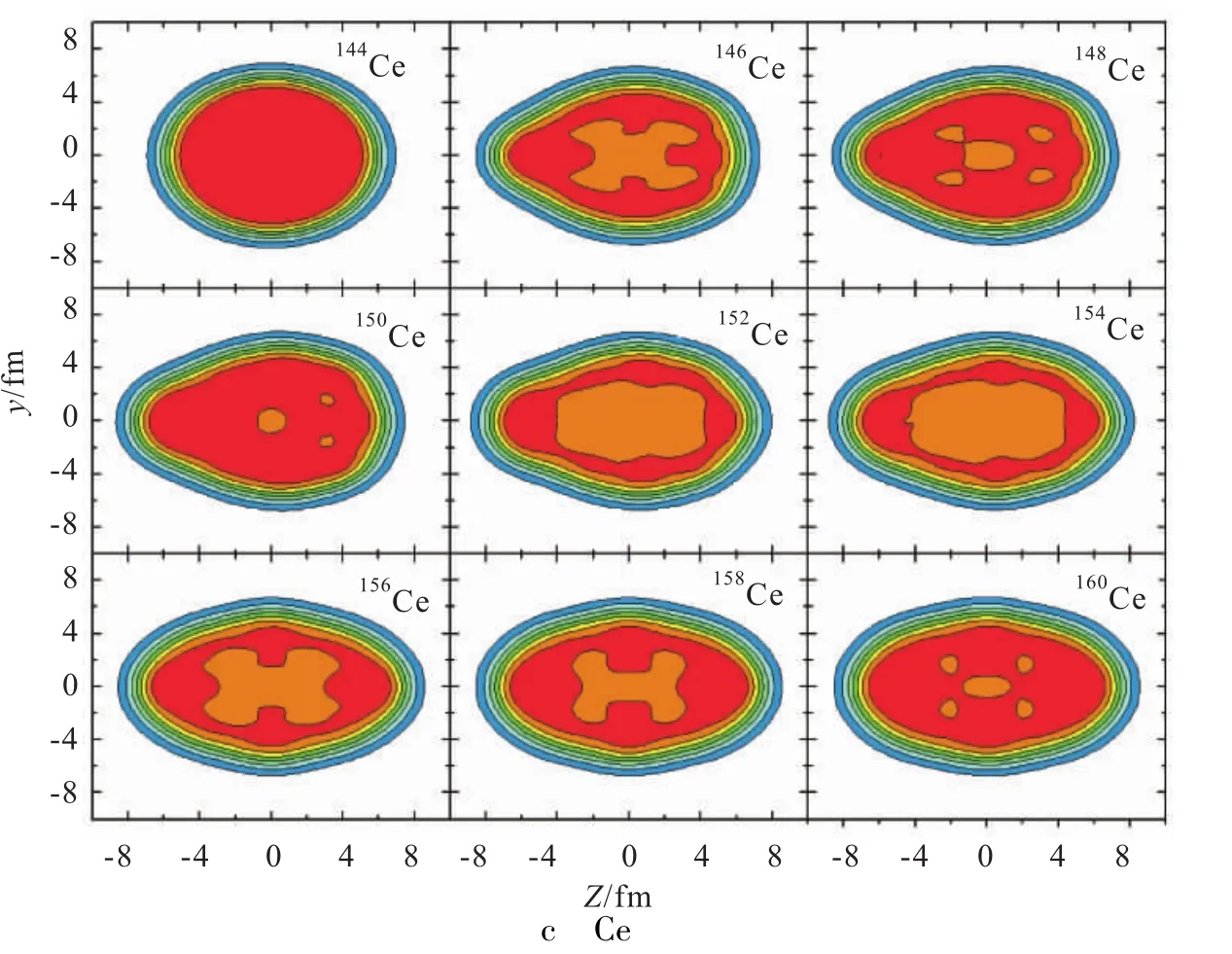
图3 Xe、Ba和Ce同位素偶偶核分别在x=0平面的质量密度分布Fig.3 Matter density distributions of the ground state of the even-even Xe，Ba and Ce isotopes on the x=0 plane

3 结束语

利用反射不对称相对论平均场(RAS－RMF)理论，计算且对比分析了Xe、Ba和Ce同位素偶偶核的基态性质及原子核形状演化.结果表明:RAS－RMF理论计算获得的核子结合能与已知的实验数据基本吻合.物质密度分布图直观地展现了Xe、Ba和Ce同位素偶偶核基态形状演化的规律.RAS－RMF理论很好地描述了Xe、Ba和Ce同位素偶偶核的基态性质.Xe、Ba和Ce同位素偶偶核都有着出现八极形变的质量数A取值范围(对Xe核，A为108～112;对Ba核，A为144～154;对Xe核，A为146～154)，质量数A在此特定范围附近取值时，原子核形状由轴对称的近球形逐渐变为不对称的梨形，最后又演化回轴对称长椭球形.

［1］Wood J L，Heyde K，Nazarewicz W，et al.Coexistence in even－mass nuclei［J］.Phys Rep，1992，215:101－201.

［2］Asaro F，Stephens F S，Perlman I.Complex alpha spectra of radiothorium(Th228)and thorium－X(Ra224)［J］.Phys Rev，1953，92:1495－1500.

［3］Stephens F S，Asaro F，Perlman I.Low－lying 1－states in even－even nuclei［J］.Phys Rev，1954，96:1568－1572.

［4］Leander G A，Sheline R K，Möller P.The breaking of intrinsic reflection symmetry in nuclear ground states［J］.Nucl Phys A，1982，388:452－476.

［5］Ring P.Relativistic mean field theory in finite nuclei［J］.Prog Part Nucl Phys，1996，37:193－263.

［6］Meng J，Zhang W，Zhou S G，et al.Shape evolution for Sm isotopes in relativistic mean－field theory［J］.Eur Phys J A，2005，25:23－27.

［7］Meng J，Peng J，Zhang S Q，et al.Possible existence of multiple chiraldoublets in106Rh［J］.Phys Rev C，2006，73:037303.

［8］Li Z P，Yao J M，NikšićT，et al.Energy density functional analysis of shape evolution in N=28 isotones［J］.Phys Rev C，2011，84:054304.

［9］Yao J M，Meng J，Ring P，et al.Microscopic description of quantum shape fluctuation in C isotopes［J］.Phys Rev C，2011，84:024306.

［10］NikšićT，Vretenar D，Lalazissis G A，et al.Microscopic description of nuclear quantum phase transitions［J］.Phys Rev Lett，2007，99:092502.

［11］Meng J，Peng J，Zhang S Q，et al.Possible existence of multiple chiraldoublets in 106Rh［J］.Phys Rev C，2006，73:037303.

［12］NikšićT，Li Z P，Vretenar D，et al.Beyond the relativistic mean－field approximation.III.collective hamiltonian in five dimensions［J］.Phys Rev C，2009，79:034303.

［13］Li Z P，NikšićT，Vretenar D，et al.Microscopic analysis of nuclear quantum phase transitions in the n approximate to 90 region［J］.Phys Rev C，2009，79:054301.

［14］Li Z P，NikšićT，Vretenar D，et al.Microscopic analysis of order parameters in nuclear quantum phase transitions［J］.Phys Rev C，2009，80:061301.

［15］Geng L S，Meng J，Toki H.Reflection asymmetric relativistic mean field approach and its application to the octupole deformed nucleus226Ra［J］.Chin Phys Lett，2007，24:1865－1868.

［16］Holzer P，Mosel U，Greiner W.Double－centre oscillator and its application to fission［J］.Nucl Phys A，1969，138:241－252.

［17］Maruhn J，Greiner W.The asymmetric two center shell model［J］.Z Phys，1972，251:431－457.

［18］Zhang W，Li Z P，Zhang S Q，et al.Octupole degree of freedom for the critical－point candidate nucleus152Sm in a reflection－asymmetric relativistic mean－field approach［J］.Phys Rev C，2010，81:034302.

［19］Guo J Y，Jiao P，Fang X Z.Microscopic description of nuclear shape evolution from spherical to octupole－deformed shapes in relativistic mean－field theory［J］.Phys Rev C，2010，82:047301.

［20］黄海，焦朋，郭建友.反射不对称自由度对原子核基态性质的影响［J］.中国科学G，2010，40:1416－1421.

［21］Long W H，Meng J，Giai N V，et al.New effective interactions in relativistic mean field theory with nonlinear terms and density－dependent meson－nucleon coupling［J］.Phys Rev C，2004，69:034319.

［22］Moller P，Nix J R.Nuclear ground－state masses and deformations［J］.At Data Nucl Data Tables，1995，59:185－381.

［23］Raman S，Nestor W J R.Transition probability from the ground to the first－excited 2+state of even－even nuclides［J］.At Data Nucl Data Tables，2001，78:1－128.