基于神经网络的流涎机组多电机同步控制研究

王 波 曹春平 胥小勇 孙 宇

南京理工大学，南京，210094

0 引言

多电机同步控制在造纸机、染整机械、纺织、薄膜生产等自动控制系统中广泛存在［1－2］。在实际应用中，由于多电机的同步控制存在参数时变、非线性、容易受负载扰动及对象模型不确定等因素，且同步性能会因各传动轴的驱动特性不匹配而恶化，因此采用传统的控制方案难以取得满意的同步控制效果。崔皆凡等［3］在改进耦合控制的基础上加入了模糊控制器，取得了较好的同步控制效果，但模糊控制的模糊规则、隶属度函数等设计参数只能依靠经验来选择，很难自动设计和调整，缺乏自学习性与适应性。刘伟等［4］在偏差耦合控制结构的基础上设计了单神经元PID控制器，并应用到多电机同步矢量控制中。曹玲芝等［5］在偏差耦合控制结构的基础上加入了滑模控制器，并将其应用到起重机起升机构的同步控制中。

本文结合流涎机组的特点提出了基于神经网络PID控制器的偏差耦合多电机同步控制策略，利用神经网络良好的自适应和自学习能力，以及无限逼近任意非线性函数的特点［6－7］，设计了神经网络PID控制器。仿真和实验结果表明，它能有效地克服系统中参数时变、非线性等问题，获得理想的同步控制效果。

1 流涎薄膜生产工艺

流涎薄膜生产工艺是指将树脂材料通过挤出机加热料筒加热至熔融塑化状态，聚合物熔体由挤出模头挤出，流涎到骤冷辊上冷却定形，然后再经过测厚、电晕处理、牵引、切边等后续工艺，最后收卷获得薄膜产品，流涎薄膜生产机组的结构如图1所示。

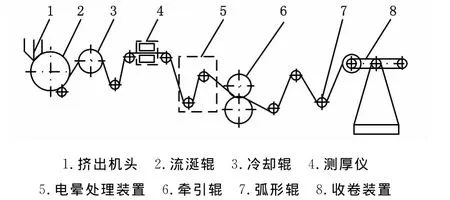
图1 流涎薄膜生产机组结构

在实际的薄膜生产过程中，从挤出、流涎、牵引到最后的收卷成形，要求各主动辊速度保持同步协调的关系，从而保持薄膜表面张力恒定，否则将发生薄膜缠绕、撕裂等现象。因此，多电机同步控制效果的好坏直接影响薄膜产品的质量。

2 流涎机组多电机同步控制结构

偏差耦合控制的主体思想是将某一台电机的速度反馈值同其他电机的速度反馈值分别做差，将得到的偏差累加起来作为该电机速度控制的补偿信号，本文将神经网络PID控制的特点与偏差耦合控制结构相结合，设计了流涎机组多电机同步控制结构。设计采用变频交流调速方案，同步控制结构如图2所示。

图2 基于神经网络控制的多电机同步控制结构

图2中，ωi（t）为第i（i＝1，2，…，n）台电机的速度反馈，ω＊i（t）为第i台电机的给定速度，定义ei（t）为第i台电机的速度跟踪误差，则

εi，j（t）为系统中第i台电机与第j（j＝1，2，…，n且i≠j）台电机的同步误差，则

因此，在一个n台电机的同步控制系统中共包括n2个控制器，其中每台电机的控制需要1个跟踪误差控制器和n－1个同步误差控制器。要使系统中各电机速度保持同步运行，则要求每台电机的跟踪误差及同步误差稳定收敛，即

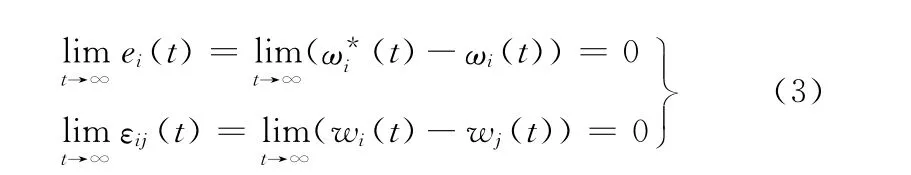
系统中各电机的速度控制量为

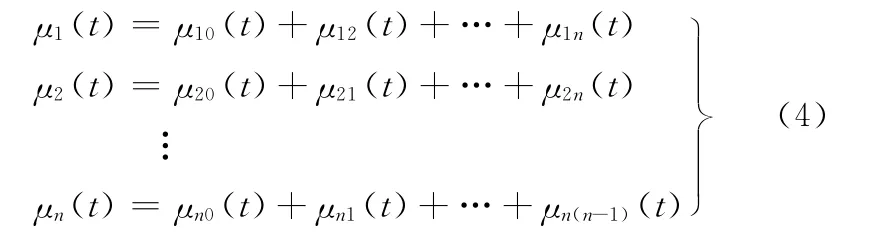
式中，μi0（t）为第i台电机跟踪误差控制器的控制输出；μij（t）为第i台电机的同步误差控制器的控制输出；μi（t）为第i台电机的速度控制量。

3 神经网络PID控制器

3.1 控制器结构

由于多电机同步控制系统在实际运行时存在参数时变、非线性、时滞等现象，而神经网络不依赖于被控对象的精确模型，并具有良好的自学习、自适应能力及非线性逼近能力。因此，本文将神经网络控制器与传统的PID控制器相结合，设计了神经网络PID控制器，如图3所示，其输入分别为ei（t）、εij（t）。

图3 神经网络PID控制器

神经网络控制器采用3层BP神经网络，其中，2个输入节点分别对应电机转速的偏差e及偏差变化率ec；输出节点分别对应PID控制器的调节参数Kp、Ki、Kd。由于 Kp、Ki、Kd不能为负值，所以网络输出层神经元活化函数取非负的Sigmoid函数，隐含层神经元活化函数取为正负对称的Sigmoid函数。Wij（k）、Wjs（k）分别为输入层与隐含层及隐含层与输出层的连接权。

3.2 控制器学习算法

根据同步系统运行状态，取性能指标函数：

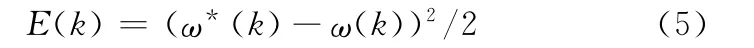
式中，ω（k）、ω＊（k）分别对应电机转速在k时刻的输出与给定。

PID控制器采用控制增量式数字PID控制，控制算式为

根据性能指标，按照梯度下降法修正网络权值，即按e（k）对加权系数的负梯度方向搜索调整，并附加一个使搜索快速收敛全局极小的惯性项，修正公式为

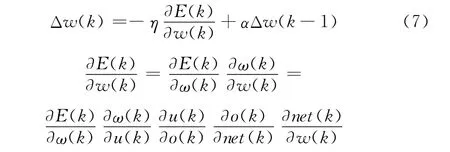
式中，η为学习速率，η＞0；α为惯性系数，0＜α＜1。

对于输出层有

综合以式（5）～式（8）可得神经网络输出层的权值学习算法公式：

同理可得隐含层加权系数的计算公式：

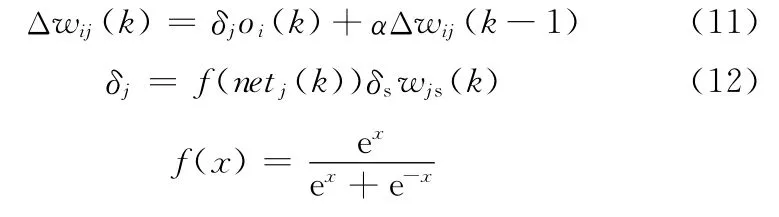
4 仿真与实验

4.1 仿真结果分析

为验证所提控制算法的稳定性和收敛性，本文采用MATLAB／Simulink搭建系统仿真平台。多电机同步系统由4台YS系列三相异步交流电机构成。4台电机模型的主要参数设置如表1所示。其中，Pe为电机功率；Rs、Rr分别为定子和转子的电阻；J为转动惯量；Ls、Lr分别为定子和转子的绕组漏感；p为极对数。

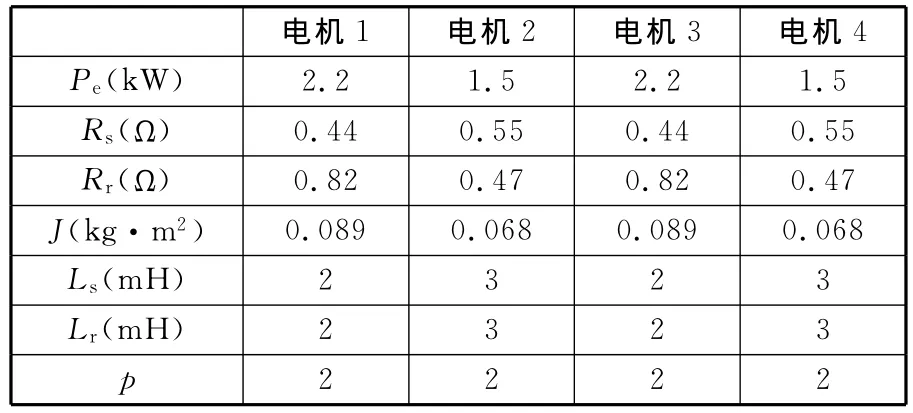
表1 电机参数设置

选取的神经网络结构为2-5-3，网络学习速率η＝0.35，惯性系数α＝0.05，加权系数初始值选取［－0.5，0.5］区间上的随机数。

仿真的控制结构如图2所示。设定4台电机的转速ω1＝ω2＝ω3＝ω4，电机给定角速度为100rad／s，在同步控制系统稳定运行之后分别在20s、35s设置扰动，结果如图4所示。

图4 偏差耦合结构神经网络PID控制仿真

从图4可以看出，4台电机同步运行时，在启动阶段，4台电机的跟踪误差均能在3s内收敛于零，系统同步误差最大为10rad／s；发生扰动时，波形产生不同程度的跳动，但能迅速收敛达到稳定，表明系统具有较好自适应性和收敛性；当出现扰动时，电机之间的同步误差波形变化很小，最大误差不超过10%，具有较高的同步精度。

在控制结构不变的基础上，控制算法采用模糊PID来实现，仿真结果如图5所示。模糊控制不依赖被控对象精确的数学模型，具有良好的控制效果和抗干扰性，但模糊控制缺乏自适应性、自学习性，在系统发生扰动时，同步误差的波动较大，收敛速度缓慢，稳定性能降低；启动阶段跟踪误差收敛时间较长，系统稳定性能和同步性能均变差。

仿真实验对比结果见表2，本文所提的控制算法在系统启动、运行或出现扰动时，都能快速稳定地实现多电机的同步运行，且同步性能优于常规的控制算法。

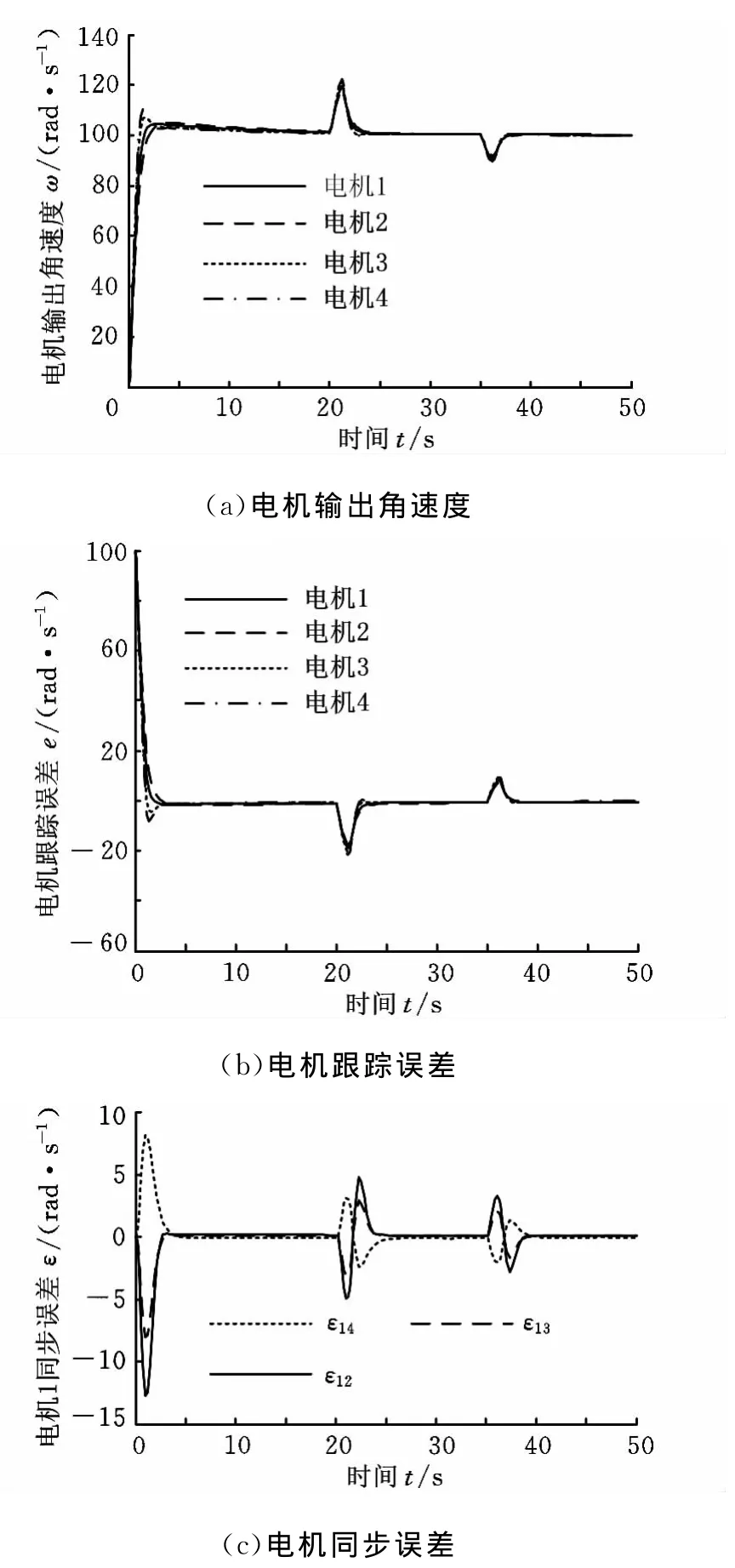
图5 偏差耦合结构模糊PID控制仿真

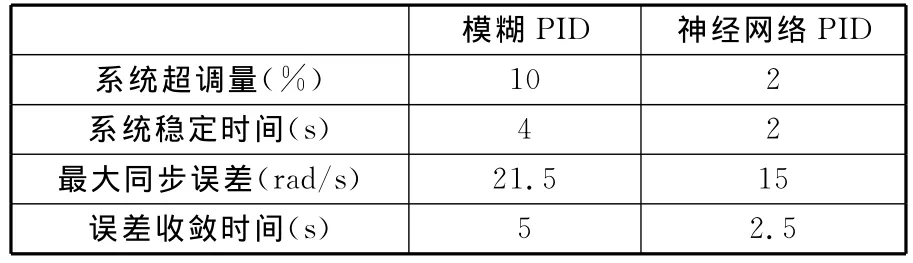
表2 仿真结果对比

神经网络通过对权值的实时修正，实现对PID控制器调节参数的在线整定，以电机1跟踪误差控制器为例，其参数自适应整定曲线如图6所示。

4.2 实际运行结果

在仿真实验的基础上，在南通三信塑胶装备科技有限公司SDLZ3000CPE型多层共挤流涎薄膜生产机组上进行验证，以牵引辊、收卷辊等4台电机为具体试验对象，4台电机具体参数的设置如表1所示。同时启动4台电机，驱动牵引辊、收卷辊同步运行，当电机速度达到13rad／s时恒速运行，运行一段时间后再升速，当速度达到38rad／s时，恒速运行一段时间后开始降速，当速度降到18rad／s时再恒速运行，并设置扰动，之后速度下降直至电机停止运转，所得结果如图7所示。

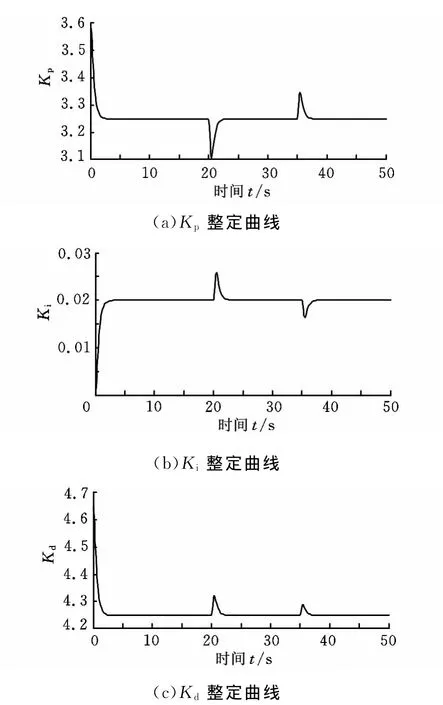
图6 参数自适应整定曲线

图7 电机实际运行曲线

从图7可以看出，4台电机在升速、恒速、降速及系统发生扰动的过程中，均能同步稳定运行。4台电机在稳态时速度的最大偏差为0.85%，系统最大同步误差为1.33%；系统发生扰动时，速度最大偏差为2.1%，最大同步误差为2.35%，体现了系统具有良好的稳定性和同步性，证明了该控制策略具有理想的动态性能和同步性能。

5 结语

本文对流涎机组多电机同步控制问题进行了研究，针对实际运行中驱动特性不匹配、负载扰动等因素的影响，及系统中存在参数时变、非线性等问题，在偏差耦合控制结构的基础上设计了神经网络PID控制器。仿真和实验结果表明，该控制策略同步控制精度高、收敛速度快、稳定性能好，能够很好地实现流涎机组的多电机的同步控制。

［1］刘福才，刘学莲，刘立伟.多级电机传动系统同步控制理论与应用研究［J］.控制工程，2002，9（4）：87－97.Liu Fucai，Liu Xuelian，Liu Liwei.Synchronous Control Theory and Practical Study of Multi－motor Synchronous Driving System［J］.Control Engineering of China，2002，9（4）：87－97.

［2］Xu Xiaoyong，Sun Yu，Fan Hongmei.Control System of the Film Casting Based on the Fieldbus［C］／／Proceedings of the 2010IEEE，International Conference on Mechatronics and Automation.Xi’an，2010：1320－132.

［3］崔皆凡，刑丰，赵楠.基于模糊控制器的改进耦合多电机同步控制［J］.微电机，2011，44（3）：75－77.Cui Jiefan，Xing Feng，Zhao Nan.The Improved Coupling Multimotor Synchronous Control Based on Fuzzy Controller［J］.Micromotors，2011，44（3）：75－77.

［4］刘伟，张翼，张勇.采用单神经元PID与偏差耦合的多电机同步矢量控制［J］.现代制造工程，2010（7）：26－34.Liu Wei，Zhang Yi，Zhang Yong.A Novel Method of Synchronized Vector Control for Multi Inductionmotor Based on Single Neuron PID and Relative Coupling［J］.Moder Manufacturing Engineering，2010（7）：26－34.

［5］曹玲芝，王红卫，李春文，等.基于偏差耦合的起重机起升机构同步控制［J］.计算机工程与应用，2008，44（25）：233－235.Cao Lingzhi，Wang Hongwei，Li Chunwen，et al.Synchronization Control in Crane Lifter Based on Relative Coupling Strategy［J］.Computer Engineering and Applications，2008，44（25）：233－235.

［6］Ding Shifei，Su Chunyang，Yu Junzhao.An Optimizing BP Neural Network Algorithm Based on Genetic Algorithm［J］.Artificial Intelligence Review，2011，36（2）：153－162.

［7］刘金琨.先进PID控制及其 MATLAB仿真［M］.北京：电子工业出版社，2003.