混合型加减速前瞻规划的多节NURBS曲线插补策略

王丽梅 刘 瑞

沈阳工业大学，沈阳，110870

0 引言

现代数控机床正在向高速高精密方向发展，数控插补技术是数控系统实现轨迹运动控制的基础，其算法是CNC系统软件实现运动控制的核心内容，插补算法的优劣直接影响到CNC系统的性能，因此实现一种高精度和高速度的插补方法是插补的关键所在。与传统的直线圆弧插补方法相比，NURBS曲线插补提供了一种通用的数学表示形式，它既可以表示标准的解析曲线，也可以表示自由曲线。NURBS插补方法以其快速性及稳定的计算能力而被普遍采用［1－2］。先进制造业的发展对数控加工的精度和速度要求越来越高。提高加工精度的途径很多，从数控系统的控制角度看，要实现高速加工，必须采用加减速控制［3］。文献［4］根据柔性加减速算法函数的构造原理，提出了三角函数加减速算法和多项式加减速算法，但是由于其情况多样，所以导致加工不够平滑。文献［5］研究了易实现控制的S曲线加减速算法，但其需要预测各段的边界点，然后再逐一进行比较，需要对加减速过程进行修正。文献［6］研究了基于NURBS曲线的插补前抛物线－直线－抛物线的S形加减速自适应控制方法，将高速加工中容易超限的弓高误差、机床所承受的加速度等参数均考虑在内，合理地解决了插补前加减速控制中的减速点预测困难的问题，但仍避免不了减速点的预测问题。

另外，CNC中的速度前瞻处理可以在不影响插补轨迹精度的前提下极大地提高插补效率［7－8］。因此，很多学者致力于前瞻算法的研究，文献［9］设计了一种基于动态前瞻的预测S曲线减速点的方法，解决了传统计算减速点存在的误差问题。文献［10］针对参数曲线插补的特点，使用S形加减速和三角函数加减速相结合的柔性加减速方法对参数曲线的插补路径进行前瞻控制。文献［11］提出了基于前瞻控制技术的误差补偿新方法。文献［12］针对基于小线段高速、高精度数控加工路径，提出并实现了一种具有速度前瞻功能的非对称S曲线加减速规划策略。以上提出的前瞻方法归结起来，无非是两种方法：一为传统的规划方法，它可以缩短加工时间，但是在转角或曲率较大的地方会造成机台的急速转弯，在实现上不可行；二为直接数字卷积法，它可以降低转角误差现象，但此方法的加工时间过于冗长，会造成加工效率的降低。

由此，本文避免了传统前瞻方法和直接数字卷积法的缺点，充分结合了两者之优点，并配以前加减速规划的优势而采用混合式数字卷积法来解决这些问题，凸轮NURBS曲线的仿真实验验证了该策略的有效性。

1 NURBS曲线插补

1.1 NURBS曲线的参数表示

二维参数曲线的总体形式可以表示为

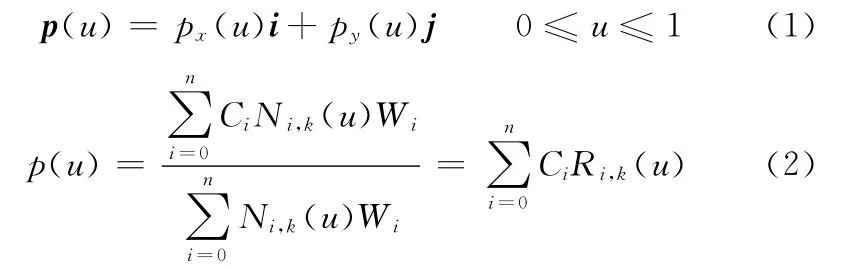
1.2 NC码与插补值命令之间的转换

下面是一段NURBS G code格式的代码：

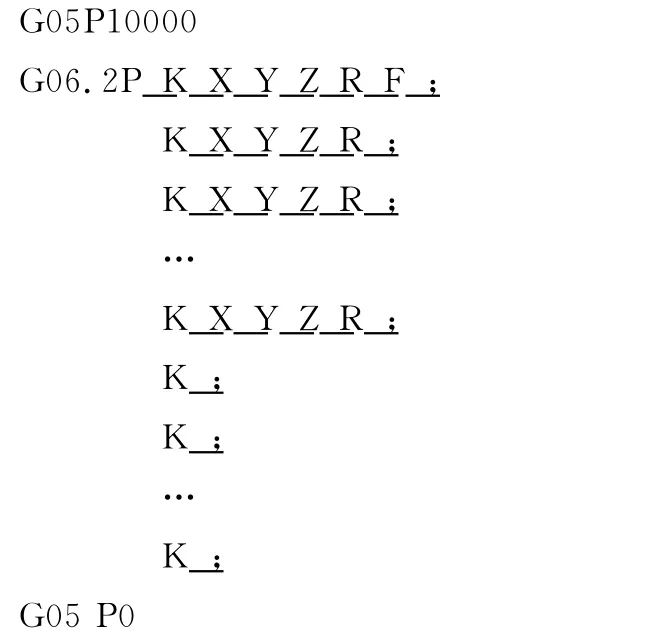
其中，P为NURBS曲线的级数，X、Y、Z为控制点坐标，R为权重，K为节点向量，F为进给率。该代码以G05P10000为开始高精度轮廓控制模式，G05P0则为结束命令，而 G06.2为开始NURBS插值模式指令。由于直接由直译器读入NURBS曲线的NC码提供了插补的完整资料—控制点、权重及节点向量，因此可以直接作为进入插补器的参数，不需要转换。

2 多节前瞻前加减速规划

2.1 加减速规划

加减速规划分为前加减速与后加减速控制，前者对于插补器来说，因为在插补之前就已经将速度命令进行规划的动作，因此在插补器执行插补时，不会有路径误差产生，所以前加减速的误差只会在命令进入到伺服回路后产生，即伺服落后的问题。后者在读入直译器的进给率后，直接进入插补器进行插补，之后再将插补器所产生的运动命令进行速度曲线的规划动作，会造成插补命令延迟，因此造成路径误差的产生，在进行圆轨迹跟踪时此现象最为明显，会产生圆半径内缩的现象。因此本文采用前加减速规划。

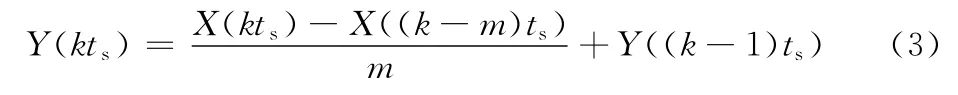
式（3）只需用到加法与除法的反复运算，因此在硬件实现上可大大减少计算机的实时计算量。

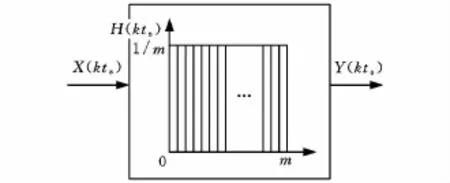
图1 数字卷积

图2为一固定进给率及一次和二次数字卷积的图形，其输入速度命令可由直译器读入其起点与终点位置，算出总长后再与所设定的进给率相除来得到总时间nts。为了要使速度曲线能够有更平滑的效果（即产生S速度曲线），可进行两次数字卷积动作，但要如何才能达到最大速度且减少整个行程的时间，取决于第二次数字卷积的H2函数的选择，为了保有其第二次数字卷积后的图形能达到最大速度，因此H2函数的时间n2ts必须比n1ts的时间短，若比n2ts时间长，则会出现速度明显达不到直译器直译出来的进给率，导致加工效率降低，因此命令数字卷积函数最后选择n1＞n2的个数才能规划出有效的命令。

图2 二次数字卷积

2.2 多节前瞻前加减速

多节前瞻前加减速分为两种：一为传统的规划方法，在命令送至插补器之前，以预读多个单节的方式求出总长，重新规划命令，但维持总长不变，依最大速度进行规划，由于有事先预读的动作，所以可以缩短加工时间，再配合前加减速的架构，也不会使其有轮廓误差产生，再将经过规划的各段速度曲线送至插补器进行插值动作，以完成前瞻的加减速；二为直接数字卷积法，当读入多个节点时，将各个单节做一次数字卷积，再将命令重新组合后，各个单节将会有不连续的速度曲线产生，因此只需将此速度曲线再进行一次数字卷积动作即可得到一平滑的速度曲线。

本文提出的混合式数字卷积法不仅改善了传统前瞻方法在转角或曲率较大的地方仍然以最大速度进行加工而造成刀具或机台在急速情况下的转弯，而需在各单节与转角处的进给率进行适当调节的状况，而且解决了直接数字卷积方法中加工时间过于冗长而导致加工效率降低的问题。如图3所示，此方法将预读多节的命令重新以最大速度进行规划，再分别对各段进行一次数字卷积动作，重新组合命令，如此每段均以最大的进给率进行加工，然后通过对此规划好的命令对整段再进行一次数字卷积动作，即可得到图3所示最终速度曲线。由图3可知，不但可借由此法来缩短加工时间，也可使机台在每一个单节不需停止即可进行下一单节的加工，这是此方法的优点所在。

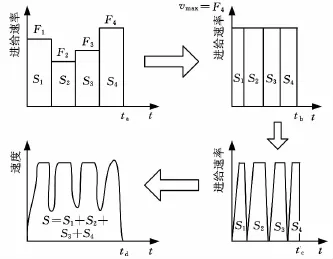
图3 混合式数字卷积前瞻命令重新规划

3 仿真结果及分析

本文将通过一条四分段的NURBS曲线插补规划来进行仿真验证。

首先进行NURBS前加减速与后加减速的速度规划与轮廓曲线比较。图4与图5分别为凸轮曲线后加减速及前加减速的速度曲线图。可以看出，在每段直线部分两者的速度曲线均相同，然而每当有圆弧曲线出现时，后加减速的速度便会降低，这也是圆内缩现象发生的主要原因所在。由这两图比较可知，在相同的进给率下，后加减速存在着圆内缩与曲线内缩的问题，因此采用的前加减速在CNC运动控制器上较为可行。

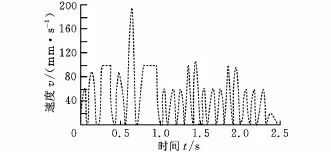
图4 后加减速插补速度规划图

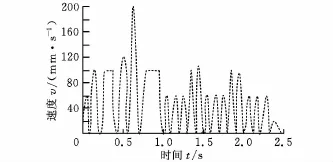
图5 前加减速插补的速度规划图

然后对前瞻规划与未前瞻规划进行比较。上述前后加减速计算均是针对每一个单节所进行的速度命令规划，再对提出的前瞻方法进行验证来证明此法的优势所在。本文待加工的凸轮曲线由四段NURBS曲线组成，因此必须先得知总长后再将命令重新进行规划。采用辛普森法来求得路径总长，传统规划方法的结果如图6、图7所示，该曲线为原先进给率命令以及经过前瞻预览处理后的速度曲线，可以看出，经过前瞻后，缩短了速度命令时间，但可看出在起点及终点附近的速度较慢。

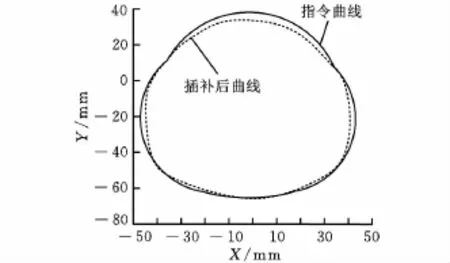
图6 后加减速的NURBS凸轮曲线

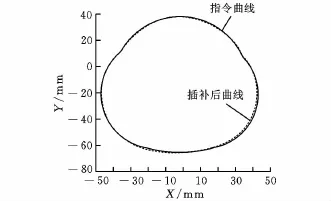
图7 前加减速的NURBS凸轮曲线

最后对多节NURBS曲线的三种前瞻方法的速度规划与轮廓曲线结果进行比较。

图8为将NURBS凸轮曲线进行传统的前瞻规划后与指令曲线的比较图，由此可知，只要事先知道总长即可重新规划速度命令。图9为其凸轮曲线图，可看出在起点及终点处点比较密集，说明有加减速的效果出现。

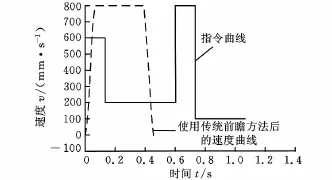
图8 传统前瞻前加减速NURBS凸轮速度曲线

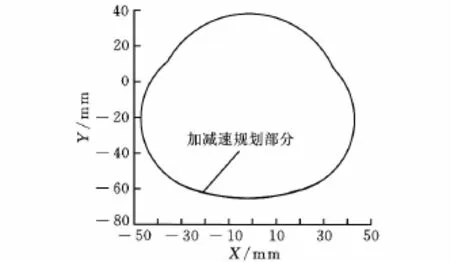
图9 传统前瞻前加减速NURBS凸轮轮廓

图10、图11分别为NURBS图形的速度分配及路径图，经过前瞻后的速度曲线图，其时间比原来落后很多，但是在其转角或急弯处有降低速度的效果产生，所以降低了转角误差，在各单节连接时也有速度减慢的效果。且可从图10看出，直接数字卷积法虽然可以降低连接处的进给率，但是却大幅度地增加整个加工时间。在路径图中，在每个转折点处，可发现点比较密集，这表明了速度的降低。

图10 直接数字卷积法的前瞻前加减速NURBS凸轮速度曲线

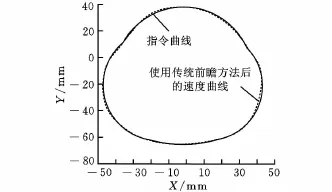
图11 直接数字卷积法的前瞻前加减速NURBS凸轮轨迹

本文提出的以混合式数字卷积法结果如图12和图13所示，两图分别为NURBS图形的速度分配及路径图，可以看出经过前瞻后的速度曲线图的时间比直接数字卷积法规划后缩短许多，且其在转角或急弯处有降低速度的效果产生，故可降低其转角误差，图13所示的路径中，每在转折点时均可发现有加减速的效果。

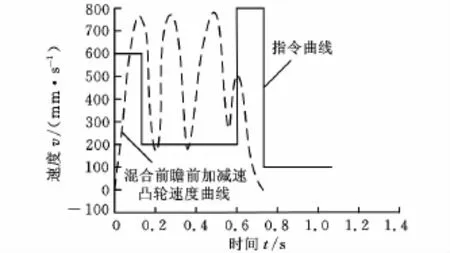
图12 混合式数字卷积法前瞻前加减速NURBS凸轮速度曲线

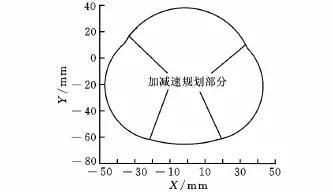
图13 混合式数字卷积法的前瞻前加减速NURBS凸轮轮廓

对比上述两种方法的速度曲线图和凸轮轮廓图可以看出，混合式方法在整体路径图上的4个转折点亦可看出其加减速效果，故混合式的数字卷积法兼具传统及直接数字卷积法的优点，为可行的前瞻方法，进而可以兼顾时间与单节连接处的加工表面品质。

4 结语

在速度命令规划方面，本文分别针对前加减速和后加减速来进行探讨，并推导出进行二次数字卷积的限制条件。在前加减速的规划方面，加入了多节前瞻的功能，以三种不同速度命令规划方式进行了比较。传统前瞻方法加工时间短，但在转折点时速度过快；直接数字卷积法虽然能在转角处降低速度，但是加工时间过长；本文采用的混合前瞻前加减速方法有效结合了传统前瞻方法和直接卷积方法的优点，使得插补的柔性和连续性得以提高。仿真结果验证了本文所提出的混合型加减速前瞻规划策略不仅可以降低加工时间，也能在转角处有降低速度的效果。

［1］刘海燕.高精度NURBS插补技术的研究［D］.北京：北京化工大学，2004.

［2］王田苗，曹宇男，陈友东，等.基于de Boor算法的NURBS曲线插补和自适应速度控制研究［J］.中国机械工程，2007，18（21）：2608－2610.Wang Tianmiao，Cao Yunan，Chen Youdong，et al.NURBS Interpolation and Feedrate Adaptive Control Based on de Boor Algrithm［J］.China Mechanical Engineering，2007，18（21）：2608－2610.

［3］朱晓春，吴祥，任浩.数控技术［M］.北京：机械工业出版社，2006.

［4］张振华.数控系统加减速算法及定位技术［D］.大连：大连理工大学，2007.

［5］朱晓春，屈波，孙来业，等.S曲线加减速控制方法研究［J］.中国制造业信息化，2006，35（23）：38－40.Zhu Xiaochun，Qu Bo，Sun Laiye.The Study on S－curve Acceleration／Decelation Control［J］.Chinese Mechanical Information，2006，35（23）：38－40.

［6］赵巍，王太勇，万淑敏.基于NURBS曲线的加减速控制方法研究［J］.中国机械工程，2007，17（1）：1－3.Zhao Wei，Wang Taiyong，Wan Shumin.Acceleration－deceleration Control Method Based on NURBS Curve［J］.China Mechanical Engineering，2007，17（1）：1－3.

［7］赵国勇，徐志祥，赵福令.高速高精度数控加工中NURBS曲线插补的研究［J］.中国机械工程，2006，17（3）：291－294.Zhao Guoyong，Xu Zhixiang，Zhao Fuling.Study on NURBS Curve Interpolator in the High Speed and High Accuracy CNC Machining［J］.China Mechanical Engineering，2006，17（3）：291－294.

［8］曹宇男，王天苗，陈友东，等.插补前S加减速在CNC前瞻中的应用［J］.北京航空航天大学学报，2007，33（5）：594－599.Cao Yunan，Wang Tianmiao，Chen Youdong，et al.Application of Pre－interpolation S－shape Acceleration／Deceleration in CNC Look－ahead Interpolation Algorithm［J］.Journal of Beihang University，2007，33（5）：594－599.

［9］李建伟，林浒，孙玉娥.基于S曲线加减速的NURBS实时插补前瞻控制方法［J］.组合机床与自动化加工技术，2009（11）：41－46.Li Jianwei，Lin Hu，Sun Yuer.A Real－time Looking－forward NURBS Interpolation Algorithm Based on S－shape［J］.Modular Machine Tool ＆Automatic Manufacturing Technique，2009（11）：41－46.

［10］王海涛，赵东标，陆永华.参数曲线柔性加减速前瞻控制算法［J］.中国机械工程，2012，23（3）：299－304.Wang Haitao，Zhao Dongbiao，Lu Yonghua.Parametric Curve Look－ahead Interpolation Algorithm with Flexible Acceleration and Deceleration Method［J］.China Mechanical Engineering，2012，23（3）：299－304.

［11］任锟，陈文华，潘骏，等.基于高速数控前瞻控制技术的误差补偿算法［J］.机械工程学报，2010，46（15）：155－160.Ren Kun，Chen Wenhua，Pan Jun，et al.Error Compensation Method Based on Look－ahead Control Technology in High Speed Numerical Control Machining［J］.Chinese Journal of Mechanical Engineering，2010，46（15）：155－160.

［12］陈光胜，梅雪松.一种小线段的非对称S曲线速度规划与前瞻算法［J］.机械设计与制造，2010（8）：47－49.Chen Guangsheng，Mei Xuesong.A Dissymmetrical S Curve Velocity Plan ＆ Look－ahead Algorithm for Small Line Segments［J］.Machine Design＆ Manufacture，2010（8）：47－49.