基于流固耦合的滑动轴承非线性油膜动特性研究

毛文贵 韩 旭 刘桂萍

1.湖南大学，长沙，410082 2.湖南工程学院，湘潭，411101

0 引言

随着机器向高速、大功率、大型化方向发展，滑动轴承越来越多地工作在高速重载的恶劣工况下，这对其性能设计提出了更加严格的要求。滑动轴承油膜动力特性系数直接影响着转子—滑动轴承系统的临界转速、不平衡响应、稳定性等动力学行为。滑动轴承油膜动特性通常可用8个系数来描述。早在1965年的时候，Lund［1］就采用4个刚度系数和4个阻尼系数建立了挠性转子系统模型，揭示了油膜涡动失稳的物理本质。这些动力系数表达了油膜的动反力和轴颈的振动位移与速度之间的定量关系，精确计算滑动轴承的动力系数对转子—滑动轴承系统动力学的研究和旋转机械的设计起着非常重要的作用。

目前，国内外学者大多通过有限差分法求解雷诺（Reynolds）方程来研究层流状态下滑动轴承的动静特性［2－3］。有限差分法通过动态雷诺方程对各项扰动参数求导，来得到各项扰动压力的微分方程，通过求解这些扰动压力的雷诺方程，得到各项扰动压力分布，并积分得到滑动轴承的线性化刚度系数和阻尼系数。然而上述研究对滑动轴承动力特性系数计算的前提是，雷诺方程中的偏心率与偏位角要等于转轴处于平衡位置时的偏心率与偏位角，而在实际求解过程中，转子的载荷可以预先指定但转轴平衡位置却是未知的，且转子从开始工作到稳定在平衡位置这段时间内，转轴的偏心率和偏位角是时刻变化的。因此采用传统静态滑动轴承动力特性系数分析转子稳定在平衡位置之前这段时间内的瞬态响应是不准确的。李元生等［4］采用有限元法和有限差分法，通过在每个时刻用学科间迭代方法来实现转子瞬态响应与滑动轴承动力特性系数分析之间的耦合。有限差分法求解滑动轴承动力特性系数至少要4次调用雷诺方程，只有单元划分足够细，方可达到理想精度，故计算量很大，而小扰动速度的界限也不太好确定，因此不适于非线性分析。

高速重载滑动轴承中，流动油膜处于转子动壁面和轴瓦静壁面之间，流速呈线性分布，接近静壁面区流速较小，为层流状态，远离静壁面区（核心区）流速较大，为紊流状态，油膜处于一种复合紊流状态［5］。肖忠会等［6－7］针对层流状态下非线性油膜力的求解提出了一种快速算法，该算法把二维变分不等方程降为一维，并将油膜力与动力特性系数联合起来一并求解，可省去诸多中间环节，计算量大为减小，另外该算法便于求解复杂区域上的问题，对于事先未知的自由边界或求解区域内部不同介质的交界面比较容易处理。本文将其拓展到紊流情况下的求解，从而利用有限变分法获得高速下径向滑动轴承层紊流下非线性油膜特性的一种快速计算方法，并通过短轴承理论公式和常用的有限差分法进行验证。

本文针对高速转子—滑动轴承系统从开始工作到稳定在平衡位置这段时间的非线性油膜动力特性系数的求解问题，提出了高速下径向滑动轴承非线性油膜动力特性系数动态分析方法。该方法考虑任意时刻转子轴心瞬态响应位移及速度与滑动轴承非线性油膜动力特性系数之间的耦合影响，采用有限变分法和Newmark－β法实现滑动轴承非线性油膜动力特性系数与转子瞬态响应之间的耦合，并以Jeffcott转子瞬态响应为例，对比研究了传统静态与本文动态非线性油膜动力特性系数分析方法。

1 基于有限变分法的油膜动力特性系数的计算

1.1 紊流瞬态下油膜变分方程

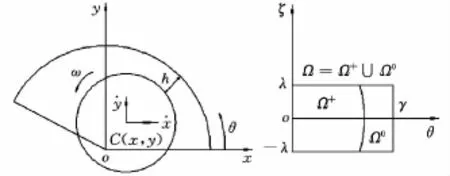
图1 轴瓦及其平面展开

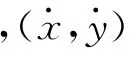
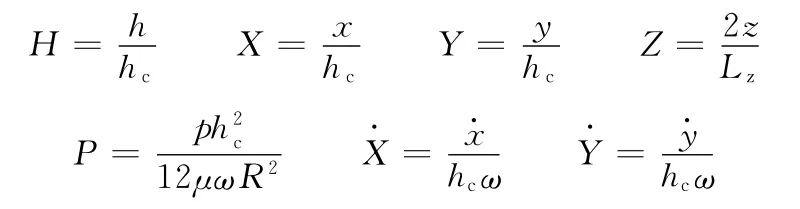
长径比为

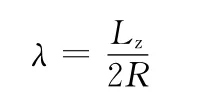
油膜流速为v时，雷诺数

紊流瞬态雷诺量纲一形式［8］如下：

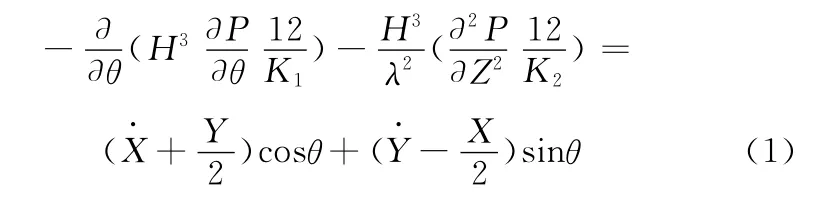
其中，K1、K2为紊流润滑系数，表达式为

油膜很薄时一般认为油膜厚度方向压力不变，沿油膜厚度方向做功微小，所以流速的变化主要由速度流引起，层紊流区域用雷诺数来区分，临界雷诺数为1000［8］。K1＝K2＝12时即可表征层流状态下的油膜特性。

郑铁生等［9］指出，二维变分法求解Reynolds边界条件下的油膜压力分布等价于求解如下算子方程：

算子L的值域为油膜润滑区域Ω：

压力分布函数q为算子方程准确解的充要条件是：当p＝q时，泛函J（q）取极小值。J（q）的表达式为

由图1所示，轴瓦润滑域为矩形，油膜破裂边虽然微曲，但其上压力及压力导数皆为零，设其为直线，对总体油膜力的影响微乎其微，故压力分布函数q可分离变量为

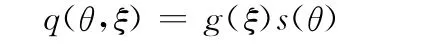
引入变分Euler方程：

从而压力函数可以通过参数Kc［6］和函数s（θ）的相互迭代修正得到，压力函数的求解转化为函数s（θ）的求解，二维方程降为一维方程。压力函数用Ritz法对s（θ）采用分段线性有限元插值函数向量r（θ）来处理，采用修正的追赶法［6］求解。油膜压力的计算转化为下式线性矩阵方程中向量a的求解：

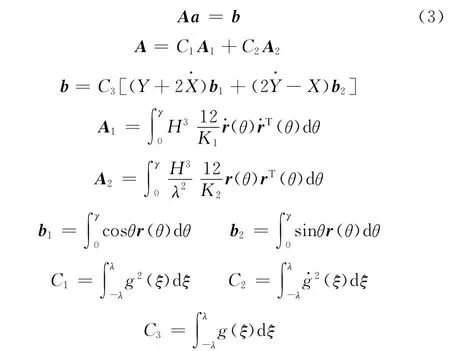
1.2 系数矩阵分解

求解式（3）可获得紊流瞬态下的油膜压力特性，但其中的系数矩阵A涉及A1和A2的求解。求解时既有对角度θ的积分，还与油膜厚度有关，油膜厚度不仅与角度θ有关，也是轴心位移的函数。将有关角度θ的积分运算和有关轴心位移的运算分离开来，每次轴心位移变化时只需按叠加处理，不必要重新积分，可大大缩短计算时间。由于

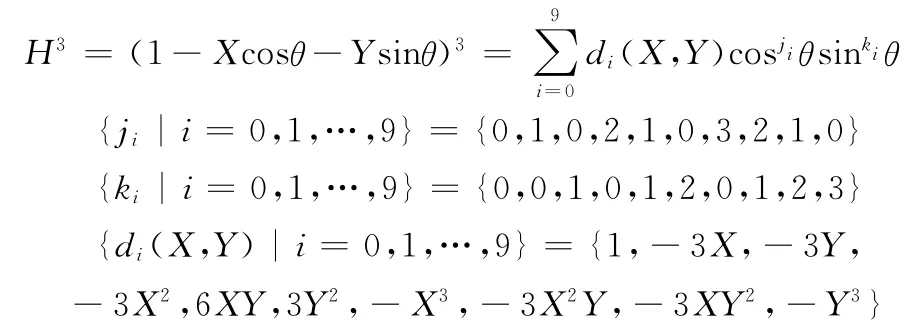
则A1及A2转化为

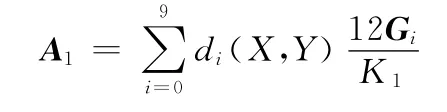
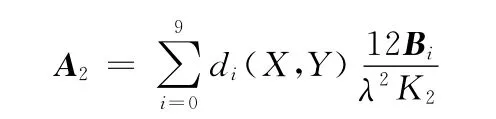
其中矩阵Gi及Bi分别为

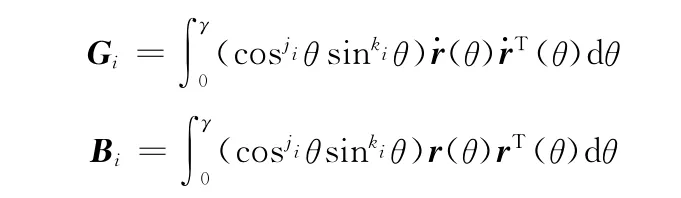
1.3 油膜力的求解

作用于轴瓦的量纲一局部油膜力（在X、Y方向上）分别为

化为整体坐标系下的油膜力分别为

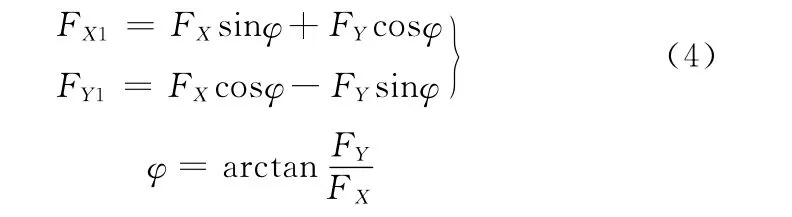
式中，φ为偏位角。

1.4 油膜刚度阻尼的计算

量纲一刚度矩阵K及量纲一阻尼矩阵C为

2 转子—滑动轴承系统动态分析方法

任意时刻转子在外激励作用下的运动微分方程为

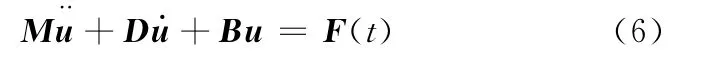
式中，u为转子轴颈轴心位移；M为质量矩阵；D为阻尼矩阵（含滑动轴承阻尼矩阵C）；B为刚度矩阵（含滑动轴承刚度矩阵K）；F为激振力。

本文采用Newmark—β法［10］分析转子系统的瞬态响应。

任意时刻，只要已知滑动轴承处轴颈中心的位移、速度，就可以通过有限变分法计算滑动轴承非线性油膜动力特性系数，同时只要知道滑动轴承的非线性油膜动力特性系数就可以通过Newmark—β法分析转子系统的瞬态响应（包括滑动轴承处轴颈中心的位移、速度）。通过以上的分析可知，转子瞬态响应分析与滑动轴承的非线性油膜动力特性系数分析是紧密耦合在一起的。所以本文将时间进行离散（时间步长为转子瞬态计算的时间步长），在每个时刻对非线性油膜动力特性系数进行迭代分析。转子—滑动轴承系统动态分析方法计算流程如图2所示。

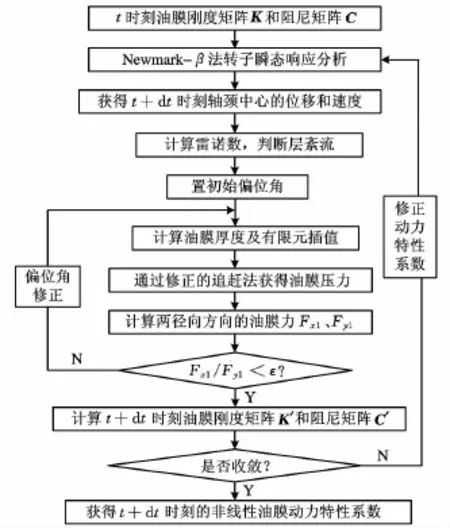
图2 转子—滑动轴承系统动态分析方法

t时刻收敛所得的非线性油膜动力特性系数矩阵K和C将作为t＋dt时刻的初值进入动态分析中；同理，t＋dt时刻非线性油膜刚度矩阵K′和阻尼矩阵C′将作为t＋2dt时刻的初值进入动态分析中。

非线性油膜动力特性系数的收敛条件为

式中，ε为迭代收敛需要满足的精度。

3 计算实例

以某Jeffcott转子系统为例进行动态分析，其转子、滑动轴承参数如表1所示。

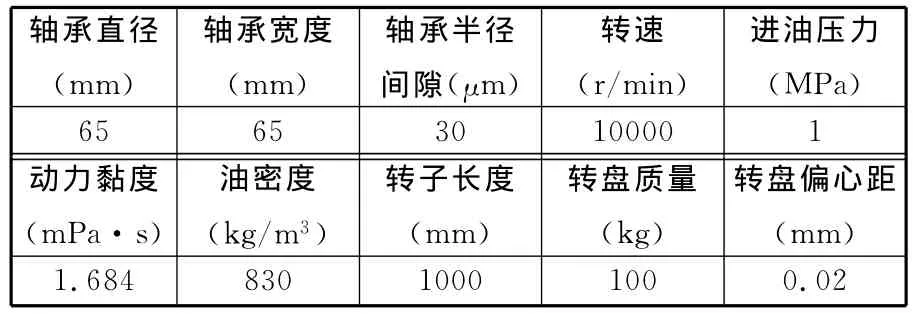
表1 Jeffcott转子系统参数

3.1 非线性油膜动力特性系数的计算

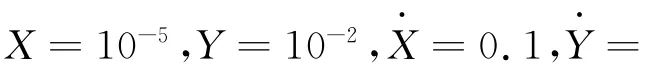
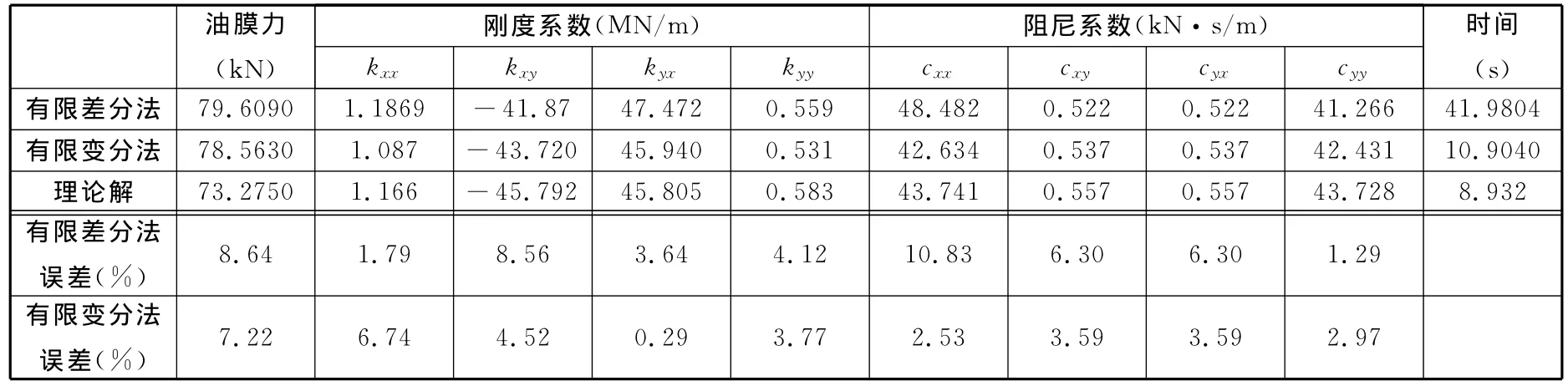
表2 滑动轴承油膜力和动力特性系数计算结果对比

3.2 Jeffcott转子系统动态分析

轴的弹性模量为200GPa，圆盘处的外阻尼系数为0.01kg／s。Newmark—β 法控制参数α ＝0.5，β＝0.25，动态分析过程的时间步长选为0.1s，总时长为12s。

图3～图5所示分别为采用本文动态滑动轴承动力特性系数方法和静态滑动轴承动力特性系数获得的12s时转子轴承处轴心的时域响应和轴心轨迹。与采用静态滑动轴承动力特性系数求得的转子轴心时域响应和轴心轨迹相比，两种方法得出的变化趋势一致，但采用动态滑动轴承动力特性系数方法获得的瞬态响应幅值更小，故采用静态滑动轴承动力特性系数设计的轴承更偏于安全，而动态分析方法精度更高。

图3 12s时转子轴承处轴心的x方向时域响应

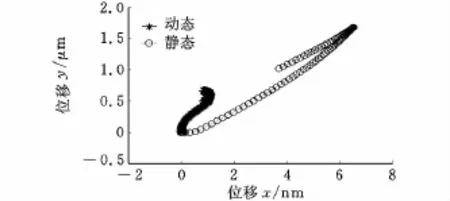
图5 12s时转子轴承处轴心轨迹

从图3～图5可知，转子启动后，在非线性油膜力的作用下，轴颈处轴心位移随时间呈周期性扰动，但最终会稳定在平衡位置。

3.3 滑动轴承动力特性系数时域响应

图6描述了滑动轴承动力特性系数随时间的变化规律。从图6可以看出，在开始时间段内，刚度系数和阻尼系数变化很大；在启动最初时间段内，转子还没有达到平衡位置，轴心涡动引起了系数的较大变化；当稳定在平衡位置后，滑动轴承动力特性系数也就趋于常数。

4 结语

转子—滑动轴承系统非线性动力学分析的一项核心内容是油膜动态特性的计算。短轴承模型实用性差；有限元或有限差分法虽然精度较高，但对于非线性分析所需的大规模数值算法而言，计算量大，求解时间长。因此，建立一种快速而实用的方法极为重要。本文通过有限变分法和Newmark—β法实现了滑动轴承动力特性系数分析与转子瞬态响应之间的流固耦合，通过学科迭代方法获得非线性油膜动态特性。与传统的静态分析方法相比，瞬态响应幅值较小，精度更高。算例表明，在确保精度的情况下，有限变分法可使运算时间大幅度缩短。

图6 滑动轴承动力特性系数时域响应

［1］Lund J W.The Sstability of an Elastic Rotor in Journal Bearing with Flexible Damped Supports［J］.ASME Journal of Applied Mechanics，1965，32（4）：911－920.

［2］庞晓平，牛坤，魏思远.用CFD方法研究具有通用膜厚方程径向轴承的动压特性［J］.中国机械工程，2012，23（21）：2521－2524.Pang Xiaoping，Niu Kun，Wei Siyuan.Research on Hydrodynamic Lubrication Performance of Journal Bearings Based on General Film Thickness Equation Using CFD Software［J］.China Mechanical Engineering，2012，23（21）：2521－2524.

［3］杨金福，杨昆，于迭仁.非线性动态油膜力及π油膜力分解的特性研究［J］.动力工程，2005，25（6）：770－779.Yang Jinfu，Yang Kun，Yu Daren.Characteristics of Nonlinear Dynamic Oil FiIm Forces and the Decomposition ofπOil FiIm Forces［J］.Chinese Journal of Power Engineering，2005，25（6）：770－779.

［4］李元生，敖良波，李磊，等.滑动轴承动力特性系数动态分析方法［J］.机械工程学报，2010，46（21）：48－53.Li Yuansheng，Ao Liangbo，Li Lei，et al.Dynamic Analysis Method of Dynamic Character Coefficient of Hydrodynamic Journal Bearing［J］.Chinese Journal of Mechanical Engineering，2010，46（21）：48－53.

［5］王小静，苏荭，张直明.基于复合型紊流润滑理论的径向滑动轴承紊流润滑性能的研究［J］.机械工程学报，2003，39（3）：85－89.Wang Xiaojing，Su Hong，Zhang Zhiming.Study on the Performance of Journal Bearing in Turbulent Regime with the Combined Reynolds Stress Model［J］.Chinese Journal of Mechanical Engineering，2003，39（3）：85－89.

［6］肖忠会，刘大全，张文，等.发电机组轴承非线性油膜力的快速算法研究［J］.中国电机工程学报，2004，24（12）：144－148.Xiao Zhonghui，Liu Daquan，Zhang Wen，et al.Study on a Rapid Algorithm for Nonlinear Oil－film Forces of Journal Bearings in Turbo－generator Unit［J］.Proceedings of the CSEE，2004，24（12）：144－148.

［7］肖忠会，王丽萍，郑铁生.滑动轴承油膜力Jacobi矩阵的一种快速算法［J］.应用力学学报，2005（1）：67－70.Xiao Zhonghui，Wang Liping，Zheng Tiesheng.A Rapid Algorithm for Jacobi Matrix Oil－film Forces of Journal Bearings［J］.Chinese Jouranl of Applied Mechanics，2005（1）：67－70.

［8］张直明.滑动轴承的流体动力润滑理论［M］.北京：高等教育出版社，1986.

［9］郑铁生，张文，马建敏，等.滑动轴承非线性油膜力的几个理论问题及应用［J］.水动力学研究与进展，2003，18（6）：761－768.Zheng Tiesheng，Zhang Wen，Ma Jianmin，et al.Some Theoretical Problems on the Nonlinear Oilfilm Forces of Sliding Bearing and Their Applications［J］.Joural of Hydrodynamica，2003，18（6）：761－768.

［10］徐斌.MATLAB有限元结构动力学分析与工程应用［M］.北京：清华大学出版社，2010.

［11］顾致平，刘永寿.非线性转子系统中的传递矩阵技术［M］.北京：科学出版社，2010.