基于可变容积力加载装置的研制

田 立，吴金波

(华中科技大学 船海学院，湖北 武汉430074)

0 引 言

船舶轴系主要由传动轴、传动部件、支撑部件以及其他一些附件组成，是船舶动力装置的重要组成部分。船舶螺旋桨的正常运行很大程度上依赖于船舶轴系工作的可靠性。研究船舶轴系的受力有助于保证轴系具有足够的强度与刚度，以便于能够正常工作［1］。

本文研究的加载装置用于模拟某船舶轴系在实际工作过程中受到的轴向外负载，可以在实验室环境下分析该轴系的动力学特性及其支撑轴承的受力情况。传统的力加载装置有弹簧加载、电动加载、电液伺服阀加载等。王辉等［2］分析了前2种加载方式的缺点并提出了改善电液伺服加载系统控制精度的方法;郭津津等［3］进行了电液比例加载系统的研究。这2 种加载方式由于受限于阀本身控制的灵敏性，加载的控制精度无法进一步提高。

李维嘉等［4］提出了一种由压力筒，用来强制改变液体体积的机械装置，计算机控制系统以及压力传感器等组成的高精度压力控制装置。该装置利用机械动力使封闭容积内液体体积发生强制改变，从而控制封闭容积内压力。本文将改变液体体积实现压力控制的方法应用于力的加载装置上。

1 工作原理

力加载装置液压部分工作原理如图1所示。

图1 液压原理图Fig.1 Hydraulic principle diagram

该装置液压部分主要由电动缸、承压筒、加载液压缸、泵及其他液压辅件组成。其中承压筒，液压缸内无杆腔以及连接的管道构成一个封闭的容积;阀门1 的作用是控制泵将油箱中的油液泵入到封闭容积或者是液压缸的有杆腔;阀门2 的作用是在失电状态下对封闭容积起到密封的作用。压力传感器的作用是作为加载装置的检测反馈元件。

在每个采样控制周期内，系统控制器根据指令加载力和实际加载力(由压力传感器反馈计算得到)之间的偏差，按照一定的控制规律计算出本采样控制周期内所需要输出的控制量，传递给电动缸驱动器，控制电动缸伸缩运动，改变封闭容积内压力，也就改变了加载力，从而达到按一定的控制精度和响应速度改变加载力的目的。

2 控制器设计

由于加载力受力面积固定，因此可以用封闭容积内的压力控制来近似代替对加载力的控制。本系统采用积分分离PID 控制算法。在偏差较大时，采用PD 控制器控制，可避免产生过大的超调，同时可以提高系统响应速率;当偏差减小到一定范围时采用PID 控制器控制，保证系统的控制精度［5］。

设定系统输出控制量为u(t)，PID 输出控制量为u(t)p，则其控制算法可以描述为

式中:ε 为分段式PID 控制的分段阈值;e(t)为系统偏差(指令信号与实际信号之间的差值)，即e(t)=Pa－Pe，Pa为系统指令压力，Pe为系统实际压力。则

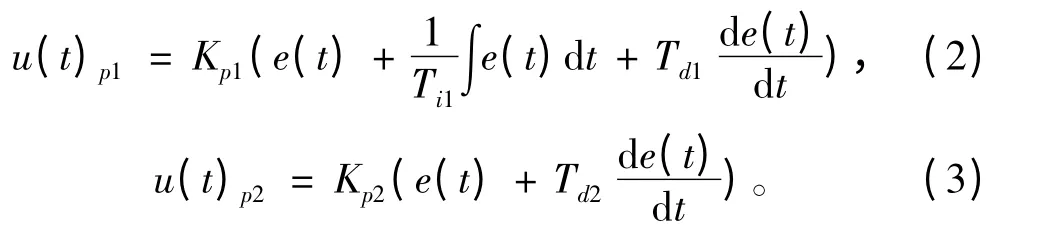
式中:Kp为控制算法比例系数;Ti为控制算法积分系数;Td为控制算法微分系数。对于高精度系统，为了提高系统的跟踪性能，在系统采用积分分离PID控制算法的同时，引入前馈补偿控制。则系统输出控制量为:

式中:Kf为前馈补偿系数;u(t)f为前馈控制输出。图2所示为力加载控制装置。

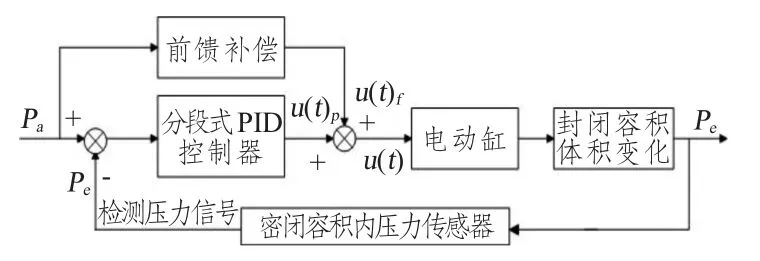
图2 系统控制方框图Fig.2 System control block diagram

3 实验研究

采用上述控制策略进行实验研究，其实验条件为:控制器为BACKHOFF PAC 控制器(可编程自动化控制器)，用ST 语言编写逻辑控制程序;系统采样控制周期为5 ms;动态加载力基础载荷为75 T，交变载荷幅值为13 T，交变频率f0最大为4 Hz，即系统指令加载力Fi=75+13sin2πf0t。系统采用的压力传感器分辨率为0.01 Ma，得到以下一系列不同交变频率时的实验结果图。

图3 中的系统指令加载力Fi=75 T，从实验结果中可知，稳态加载时系统最大偏差为0.6 T，从而得到系统的稳态加载精度为0.8%。

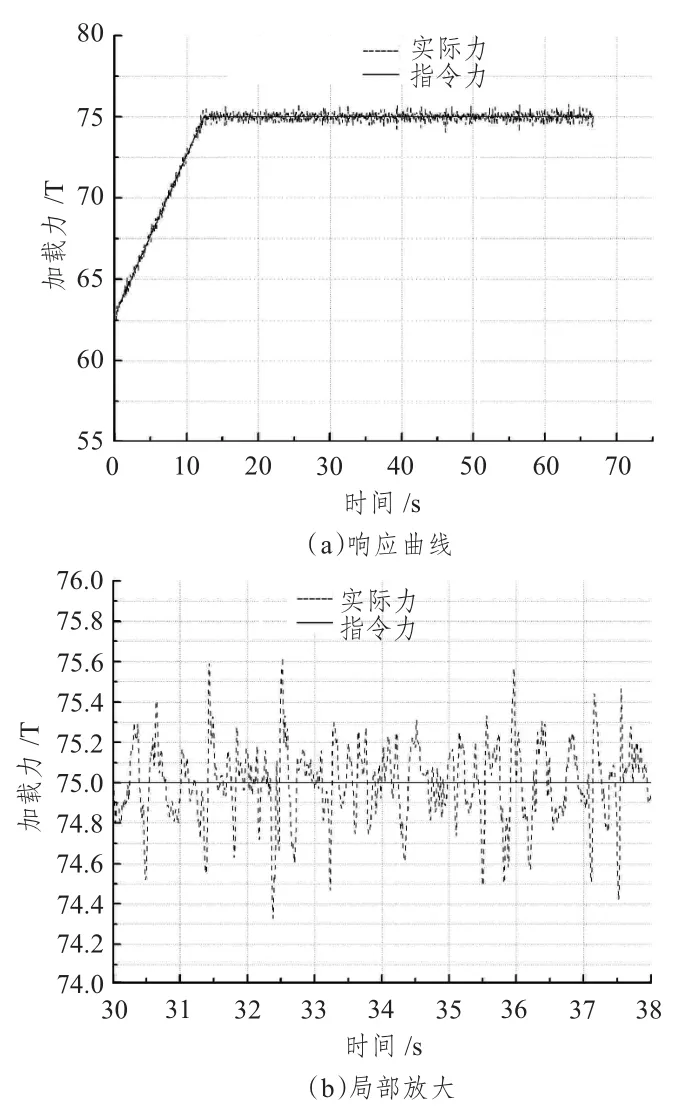
图3 稳态加载结果图Fig.3 The steady-state loading result figure

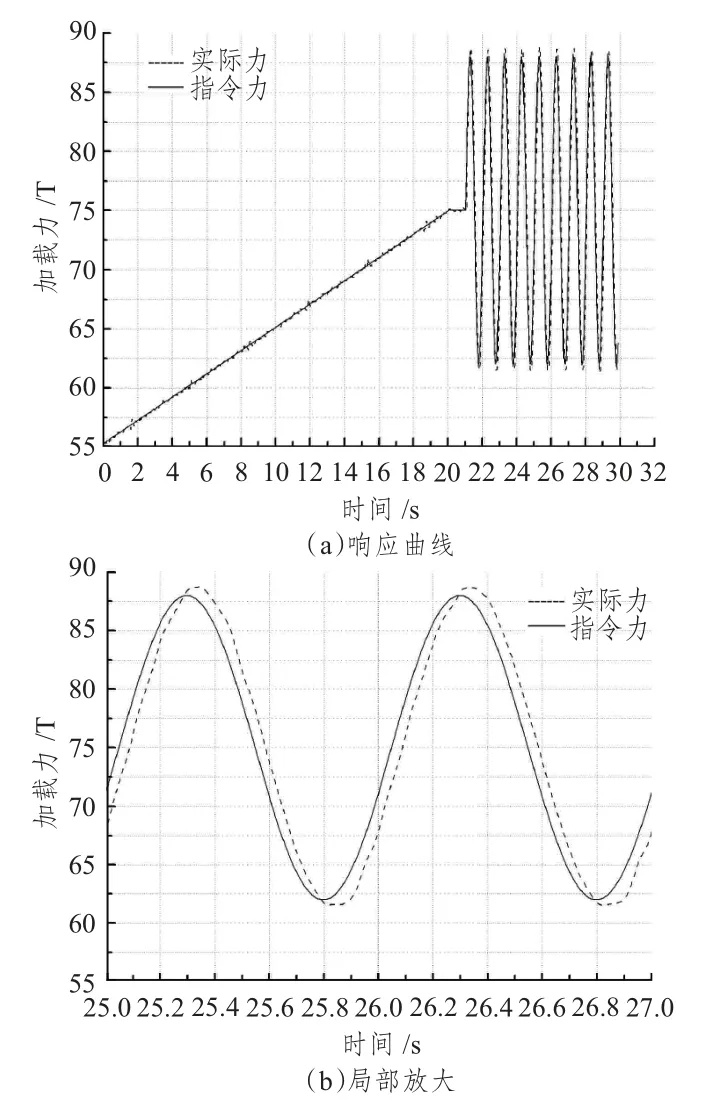
图4 动态加载1 Hz 结果图Fig.4 Dynamic loading 1 Hz result figure

图4 中的指令动态加载力Fi=75+13sin2πtT，从实验结果可知，动态加载力交变频率为1 Hz 时，系统幅值误差为1.8%，相位滞后角度为9°。

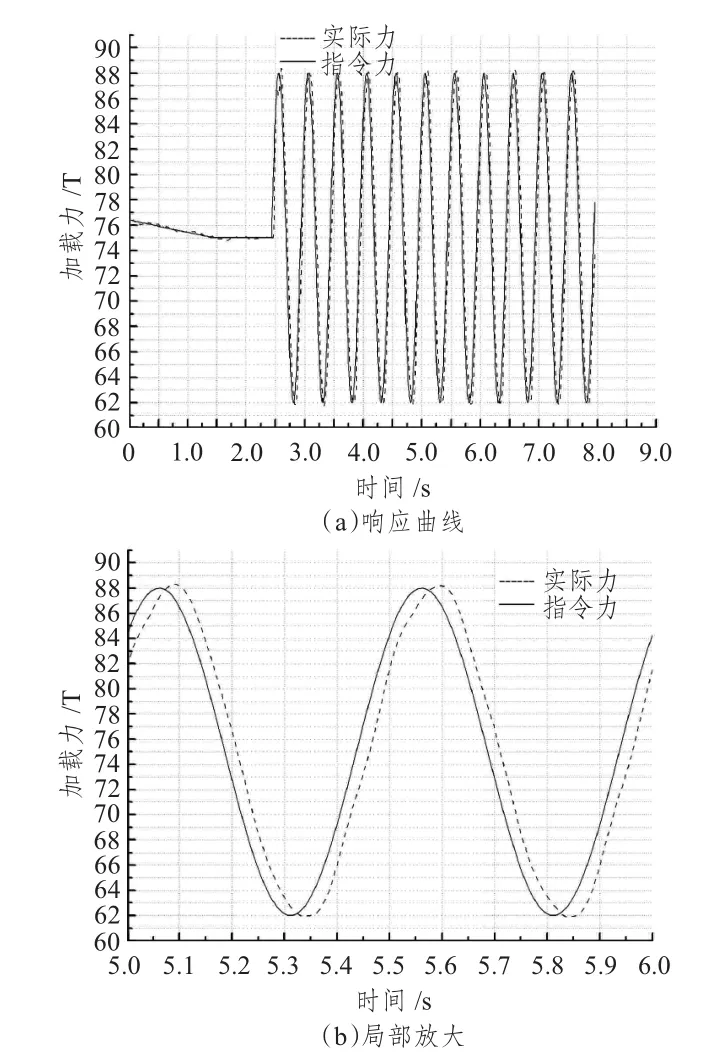
图5 动态加载2 Hz 结果图Fig.5 Dynamic loading 2 Hz result figure

图5 中的指令动态加载力Fi=75+13sin4πtT，从实验结果可知，动态加载力交变频率为2 Hz 时，系统幅值误差为0.26%，相位滞后角度为18°。

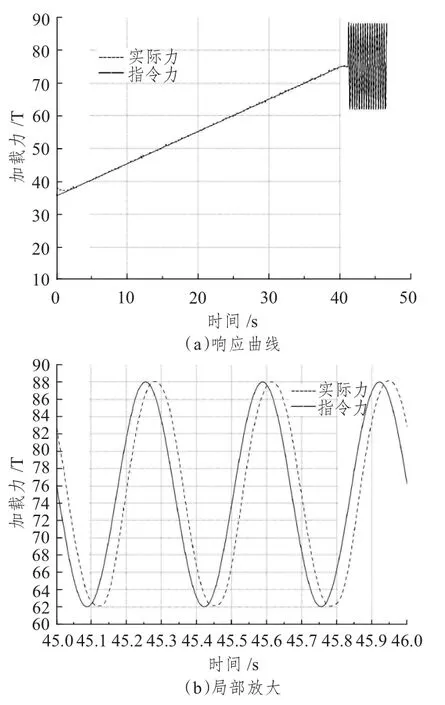
图6 动态加载3 Hz 结果图Fig.6 Dynamic loading 3 Hz result figure

图6 中的指令动态加载力Fi=75+13sin6πtT，从实验结果可知，动态加载力交变频率为3 Hz 时，系统幅值误差为0.19%，相位滞后角度为27°。

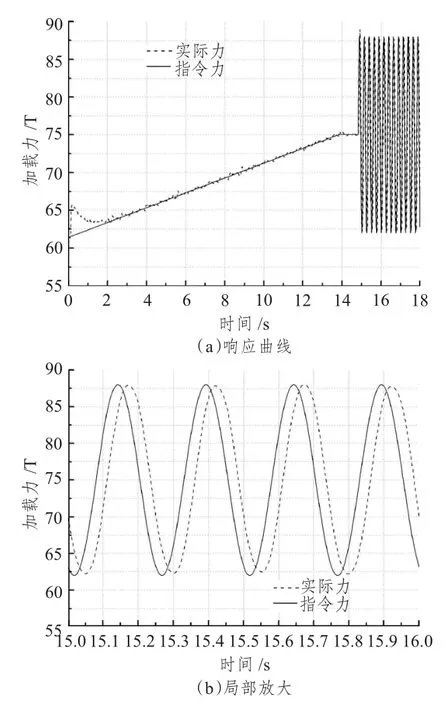
图7 动态加载4 Hz 结果图Fig.7 Dynamic loading 4 Hz result figure

图7 中的指令动态加载力Fi=75+13sin8πtT，从实验结果可知，动态加载力交变频率为4 Hz 时，系统幅值误差为0.15%，相位滞后角度为36°。

以上实验结果表明，本文研制的加载装置对于动态指令力存在着较大的相位滞后。这是由传感器、数据处理、驱动器和执行机构等环节的滞后所带来的;封闭容积中的油液混有一定量的气体，其弹性模量会随着压力的变化而变化［6］，这也会带来一定的相位滞后。系统实验结果中幅值误差通过调整控制参数已经被控制在允许范围内，还需要消除系统相位滞后。

4 滞后补偿

将以上实验结果中相位滞后角度及滞后时间按动态加载时交变频率的不同记录于表1。

表1 相位滞后随频率的变化Tab.1 Phase lag changes with frequency

因为系统采样控制周期为5 ms，所以滞后时间选取为5 ms 的整数倍。通过表1 可以发现，对于不同的动态加载交变频率，虽然相位滞后角度各有不同，但相位滞后的时间大致相同。从工程实现角度，可将本加载装置的相位滞后简化为一个纯滞后环节。在每一个采样控制周期，对任意控制时刻，采用超前25 ms 的指令加载力来代替当前时刻的指令加载力，然后再按照控制算法确定系统输出控制量，从而实现一种简单的超前补偿控制方法。

按上述滞后补偿方法得到动态加载时不同交变频率系统实验结果如图8所示。

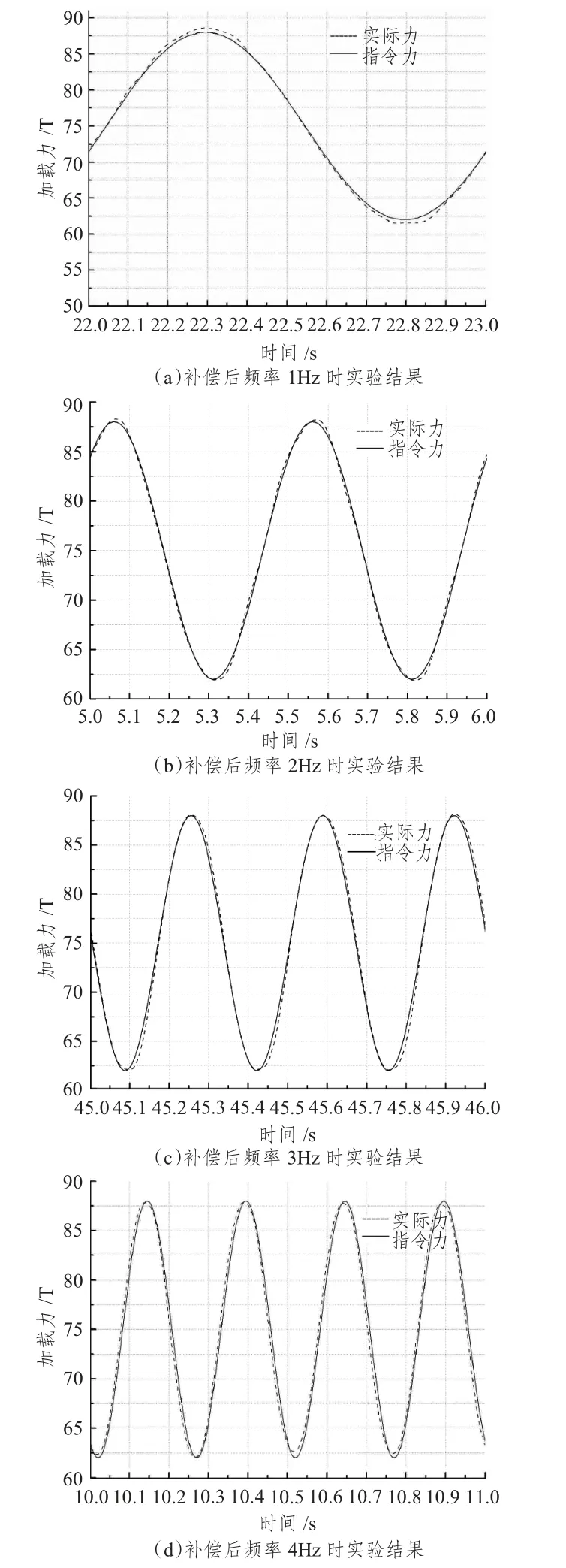
图8 相位补偿后系统实验结果图Fig.8 The result figure after phase compensation

由图8 实验结果可看出，系统经过预测补偿消除相位滞后，系统动态加载幅值误差在2%以内，相位滞后在1°以内，达到了较好的控制效果，且本文所研究的力加载装置加载连续稳定，无突然跳变现象。

5 结 语

本文所研究的力加载装置根据密闭容积内电动缸伸缩改变容积内液体压力研制而成，结构优良，加载稳定，具有良好的动态和稳态精度。目前，本加载装置已应用于某船舶轴系受力检测分析装置，效果良好。

［1］艾维，方开翔．船舶轴系力学建模与仿真研究［J］．造船技术，2007(4):42－43．

AI Wei，FANG Kai-xiang．Ship shafting mechanics modeling and simulation［J］．Shipbuilding Technology，2007(4):42－43．

［2］王辉，许守林，冯英进，等．飞行模拟器操纵负荷力加载控制系统的实验研究［J］．中国机械工程，2008，7(2):1720－1723．

WANG Hui，XU Shou-lin，FENG Ying-jin，et al．Testing research for control loading system of flight simulator［J］．China Mechanical Engineering，2008，7(2):1720－1723．

［3］齐心，郭津津．电液比例加载系统的研究和优化［D］．天津:天津理工大学，2013:1－5．

QI Xin，GUO Jin-jin．The study and optimization of the electro-hydraulicproportional force control system［D］．Tianjin:Tianjin Polytechnic University，2013:1－5．

［4］罗声，李维嘉，张金喜．基于改变容积的高精度压力控制系统的研究［J］．液压与气动，2007(5):18－19．

LUO Sheng，LI Wei-jia，Zhang Jin-xi．A high precision pressure control system based on the controllable varied volume of contained liquid［J］．Hydraulic and Pneumatic，2007(5):18－19．

［5］刘金琨．先进PID 控制及其MATLAB 仿真［M］．北京:电子工业出版社，2003．

LIU Jin-kun．Advanced PID control and MATLAB simulation［M］．Beijing:Publishing House of Electronics Industry，2003．

［6］YU Jing-hong，CHEN Zhao-neng，LU Yuan-zhang．The variation of oil effective bulk models with pressure in hydraulic systems［J］．J DYN SYST－T ASME，1994，3(116):146－150．