基于混合优化策略的多学科协同优化及其应用
2014-12-05张立丽
许 辉,周 奇,张立丽
(1.中国舰船研究设计中心,湖北 武汉430064;2.江苏自动化研究所,江苏 连云港222006)
0 引 言
船舶作为一个复杂的庞大系统,涉及到操纵、阻力、耐波、结构、振动与噪声、工艺、材料等多个方面,这些方面之间存在着相互影响、相互制约的耦合关系,因此船舶设计是一个多学科、多变量、多约束的复杂工程设计问题。就传统方法而言,船舶设计过程中对每个专业的分析单独进行,设计问题是以串行设计的方法来解决。为了追求整体最优,设计者往往需要对整个设计流程进行反复迭代,每进行一次循环,都要做大量的协调工作,不可避免地导致设计周期过长的问题。同时,由于割裂了学科间耦合关系,设计的结果往往失去了全局最优性,而陷入局部最优。
20世纪80年代,多学科设计优化(multidisciplinary design optimization,MDO)兴起于航空航天领域,以Sobieski和Kroo 为代表的科学家在这方面做了开创性的工作[1-2]。MDO 是一种通过充分探索和利用工程系统中相互作用的协同机制来设计复杂产品及其子系统的方法论[1]。随着MDO的发展,涌现出诸如多学科可行方向法(multidisciplinary feasible method,MDF)、单学科可行方向法(individual discipline feasible,IDF)、并行子空间优化算法(concurrent subspace optimization,CSSO)、协同优化算法(collaborate optimization,CO)、两级集成系统综合(bi-ievel integrated system synthesis,BLISS)等优化框架。其中,Kroo 等[3]提出的协同优化算法由于具有良好的学科自治性和并行处理能力,一直被认为是多学科优化中最具前途的优化算法。
本文在分析传统CO 求解多学科设计优化问题易出现缺陷原因的同时,提出一种基于模拟退火算法和序列二次算法的混合协同优化,并将其应用于齿轮减速箱和纤维加强型悬臂梁轻量化设计优化问题中验证其有效、实用性。
1 基于混合优化策略的协同优化
1.1 协同优化算法的数学描述及求解流程
CO 是Kroo 等针对单级多学科优化方法在解决大型复杂系统工程时出现的低效率和大计算量问题,提出的具有两级结构的多学科优化策略。CO 将优化问题分为一个系统级和并行的多个学科级。
系统级的数学描述形式如下:

CO 算法的学科级数学描述形式为:
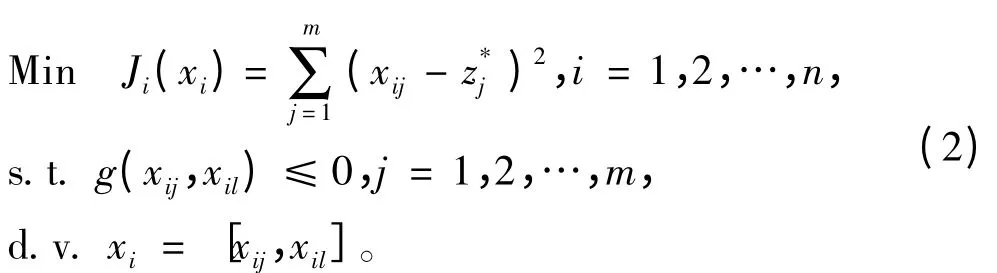
式中:Ji(xi)为学科级的优化目标函数;xij为学科级i 的第j 个共享变量;xil为学科级i 的局部设计变量;为系统级传递给学科级i 的第j 个共享变量;g(xij,xil)为学科级局部约束条件。
1.2 基于混合优化策略的协同优化
虽然CO 在工程应用领域得到了广泛的应用,但CO 的收敛性并没有得到严格的数学证明。同时,在实际运用过程中CO 表现出计算方面的困难。NASA 在IDF、MDF 及CO 的收敛性能进行测试与评估的过程中,发现CO 解决齿轮减速箱、电器封装、丙烷燃烧等十大测试实例存在计算成本大、对初始点敏感甚至无法收敛等缺陷。究其原因在于CO 独特的一致性约束表现形式:CO 算法中系统级优化的一致性等式约束条件形式是2-范数形式,其导数在最优解处的Jacobia 矩阵是奇异矩阵将导致系统级Kuhn-Tucker 条件无法满足,优化求解时采用基于梯度的优化方法,常出现无法收敛或收敛陷入局部最优的尴尬境地。针对这种情况,国内外学者继承标准CO 两级优化框架的基础上致力于提高CO 的数值稳定性。研究工作主要包含2 个方面:一是采用近似技术建立系统级约束的代理模型降低计算成本,光滑数值噪声[5-6]。如响应面近似模型、径向基神经网络模型、Kriging 模型;另一方面是采用罚函数的方法将系统级有约束问题转化为无约束优化问题,以降低优化迭代难度,提高总体收敛效率[7-8]。
随着计算机技术的飞跃发展,遗传算法、模拟退火算法、粒子群算法等现代智能优化算法在系统工程、自动化、航空航天、船舶与海洋工程等领域得到了广泛地应用。若采用具有优秀全局搜索能力的智能算法取代系统级中基于梯度的优化算法,在一定程度上能保证协同算法的鲁棒性,但应该注意智能算法需要更多的目标函数和约束函数的计算次数,当各学科的分析模型很复杂时,会导致计算成本过大的问题。文献[9]从理论上证明了在系统级优化中,当初始点已在最优解附近时,基于梯度的优化算法能迅速地收敛到最优解。综合以上分析提出基于混合优化策略的协同优化。
SA-SQP-CO 在继承标准协同优化学科自治和并行设计的基础上作了以下2 个方面的改进:
1)采用具有全局搜索能力的模拟退火算法和基于梯度的序列二次优化的混合策略取代传统协同优化系统级中的基于梯度的优化算法。
SA 算法是一种启发式的随机寻优算法,它模拟了物理退火过程,从一个给定的初始高温开始,利用具有概率突跳特性的Metropolis 抽样策略在解空间中随机搜索,伴随温度的不断下降重复抽样过程,最终得到问题的全局最优解。SA 具备优秀的全局搜索能力,但在求解过程中,当搜索到最优解附近解域时,收敛速度迅速降低大大增加了计算成本,此时采用SQP 算法进行替代SA 算法能迅速收敛。
SA-SQP-CO 具体流程如图2所示。
2 算例分析
2.1 齿轮减速器优化问题
齿轮减速器优化算例是NASA 评估多学科设计优化方法性能的10 个标准算例之一[10]。该设计问题包括7 个设计变量,如图3所示,其中x1为齿面宽度,x2为齿轮模数,x3为小齿轮齿数,x4和x5为轴承间距,x6和x7为轴的直径。目标是满足齿轮的弯曲应力和接触应力以及轴的位移和应力等约束条件下使得减速箱的质量最轻。其优化数学模型表述如下:
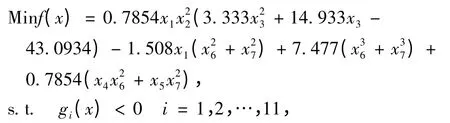
其中:

式中:

以上各式中,设计变量取值范围为:2.6 ≤x1≤3.6,0.7 ≤x2≤0.8,17 ≤x3≤28,7.3 ≤x4,x5≤8.3,2.9 ≤x6≤3.9,5 ≤x7≤5.5(单位:cm)。
按照多学科协同优化设计思想,将齿轮箱优化设计问题分解为1 个系统级和3 个学科级,系统级设计变量为z1,z2,z3,学科1 的设计变量为x1,x2,x3,x4,x6;学科2 的设计变量为x1,x2,x3,x5,x7;学科3 的设计变量为x1,x2,x3。
按照CO 算法的思想,对优化模型进行改造如下:
1)系统级优化模型

式中:

2)子学科1 的优化模型
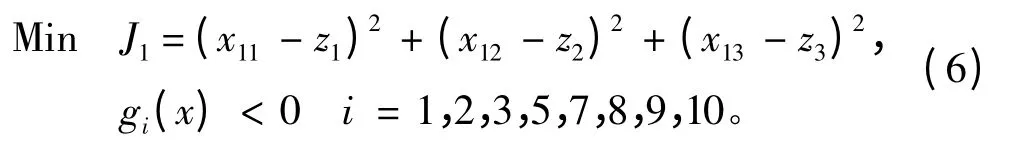
3)子学科2 的优化模型
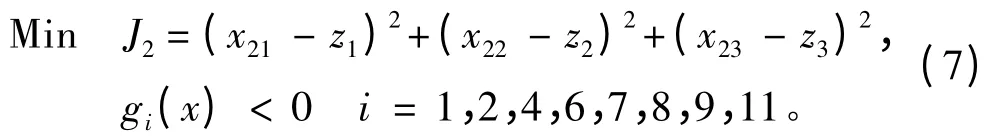
4)子学科3 的优化模型

表1 列出了NASA 给出的4 个不同起始点,其中A,B,C 为可行域内的点,D 为可行域外的点。

表1 初始设计点Tab.1 Initial design points
为便于传统协同优化收敛,采用Alexandrov 提出的松弛因子法,将系统级一致性等式约束,i=1,2,3 作松弛处理为,ε=10-4,i=1,2,3。求解时系统级采用可行方向法,学科级采用序列二次规划法,4 个初始点下的优化结果如表2所示。
SA-SQP-CO 模拟退火优化阶段中松弛因子ε1取10-2,序列二次优化阶段ε2取10-5。4 个初始点下的优化结果如表3所示。

表2 传统CO 优化结果[8]Tab.2 The optiminal results of traditional CO

表3 SA-SQP-CO 优化结果Tab.3 The optiminal results of SA-SQP-CO
由表2和表3 可看出,在起始点A 处,松弛CO算法无法收敛。SA-SQP-CO 系统经过二阶段优化迭代其优化目标值为2 987.706 kg,略小于文献[11]给出的参考值2 994 kg,降低了齿轮箱的质量,说明采用SA-SQP-CO 能有效解决协同优化算法收敛性差的缺陷,同时避免了求解陷入局部最优的问题。
当起始点选在最优解附近C和可行域外D 时,松弛协同优化和SA-SQP-CO 都能收敛至最优,但从优化结果可以看出SA-SQP-CO 的优化解基本一致即鲁棒性要优于松弛协同优化。图4 给出了不同初始点下系统级目标函数迭代过程。

图4 不同起始点处SA-SQP-CO 系统级迭代历史Fig.4 System-level iteration history of SA-SQP-CO at different points
3 悬臂梁优化问题

其中:

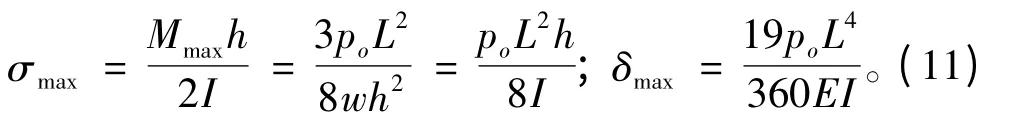

图5 承受抛物线型载荷的纤维加强悬臂梁Fig.5 Fiber-reinforced composite cantilever beam subject to a parabolic distributed load

表4 参数意义及取值Tab.4 Values and meanings of the remain variables
按照协同优化框架将此优化问题分解为一个系统级和应力、变形2 个学科级优化问题。应力学科1 的约束条件为g1,g3,g4,g5,变形学科2 的设计变量为g2,g4,g6。优化模型如下:
1)系统级优化模型

2)子学科1 的优化模型
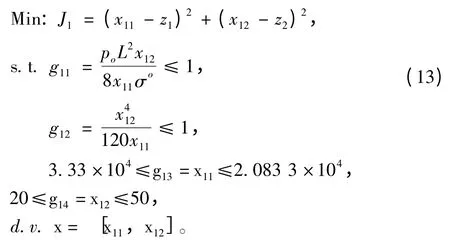
3)子学科2 的优化模型

分别采用CO和SA-SQP-CO 对优化问题求解,优化结果列于表4 中。从结果可看出,CO和SA-SQP-CO 均能获得较初始点更优的解,但SA-SQP-CO 下降优化程度更大,其中CO 较初始质量下降21.11%,SA-SQP-CO 下降38.78%。从最优化设计方案处各约束条件的取值来看,SA-SQP-CO 优化算法获得的方案能更大程度的利用材料。
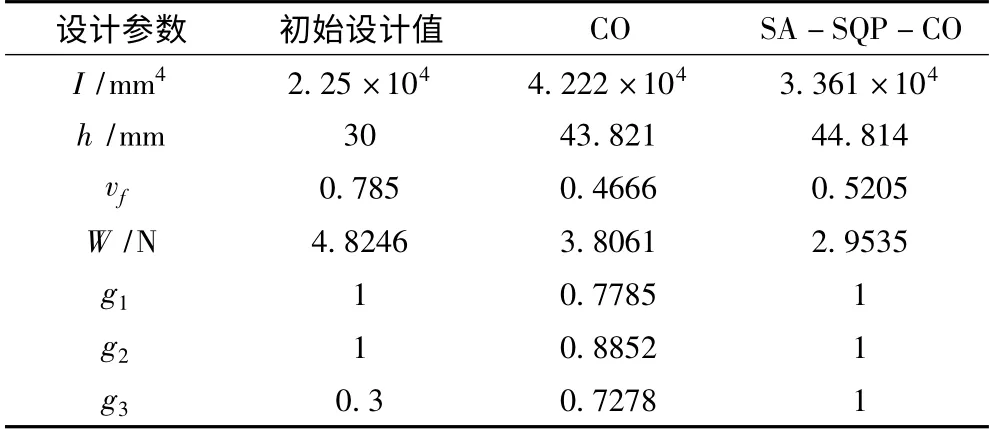
表5 优化结果比较Tab.5 Comparison results between CO and SA-SQP-CO
4 结 语
分析了标准协同优化求解多学科问题易出现缺陷原因的同时,提出了一种基于模拟退火算法和序列二次算法的混合协同优化。齿轮减速箱优化和纤维加强型悬臂梁轻量化问题表明SA-SQP-CO 相对于标准协同优化算法主要有如下优点:
1)采用模拟退火算法来优化系统级,避免了基于梯度的优化算法对数学模型表达形式的挑剔,当模拟退火算法搜索到最优解域附近时采用序列二次算法大大加快系统级收敛速度。同时,模拟退火算法和序列二次算法混合策略显著提高了优化解的全局最优性;
2)在二阶段优化过程中采用动态松弛因子,提高了收敛效率。
在舰船多学科优化运用中,各学科分析可以引入各类先进的数值仿真软件。如快速性学科的Fluent,Shipflow 等,操纵性学科的Shipma,Napa 等替代经验公式来提高设计精度。
[1]SOBIESZCZANSKI-SOBIESKI J,HAFTKA R T.Multidisciplinary aerospace design optimization:survey of recent developments[J].Structural and Multidisciplinary Optimization,1997,14(1):1-23.
[2]SOBIESKI I P,KROO I M.Collaborative optimization using response surface estimation[J].AIAA Journal,2000,38(10):1931-1938.
[3]KROO I,ALTUS S,BRAUN R,et al.Multidisciplinary optimization methods for aircraft preliminary design[J].AIAA Paper,1994,4325.
[4]YANG X X,ZHANG W H.Multidisciplinary design optimization of solid launch vehicles based on collaborative optimization[J].Journal of Solid Rocket Technology,2011(6):002.
[5]蒋平,匡玲,邵新宇,等.基于近似模型的两级集成系统协同优化方法[J].中国机械工程,2012,23(004):395-402.
JIANG Ping,KUANG Ling,SHAO Xin-yu,et al.A new blissco method based on approximate models[J].China Mechanical Engineering,2012,23(004):395-402.
[6]ZHAO M,CUI W C.Application of the optimal latin hypercube design and radial basis function network to collaborative optimization[J].Journal of Marine Science and Application,2007,6(3):24-32.
[7]李海燕,马明旭,黄章俊,等.自适应罚函数协同优化算法[J].系统仿真学报,2009(19):6178-6182.
LI Hai-yan,MA Ming-Xu,HUANG Zhang-jun,et al.New adaptive penalty scheme for collaborative optimization[J].Journal of System Simulation,2009(19):6178-6182.
[8]韩明红,邓家禔.协同优化算法的改进[J].机械工程学报,2007,42(11):34-38.
HAN Ming-hong,DENG Jia-ti.Improvement of collaborative optimization[J].Chinese Journal of Mechanical Engineering,2007,42(11):34-38.
[9]DE Miguel A V.Two decomposition algorithms for nonconvex optimization problems with global variables[D].Stanford University,2001.
[10]KODIYALAM S.Evaluation of methods for multidisciplinary design optimization(MDO),Phase I[M].National Aeronautics and Space Administration,Langley Research Center,1998.
[11]PADULA S L,ALEXANDROV N,GREEN L L.MDO test suite at NASA langley research center[J].AIAA Paper,1996,96:4028.
