高分辨率拉东变换在阵列声波测井波场分离中的应用

王明方，陆云龙，王勇

（1.中国石油集团测井有限公司，陕西 西安710077；2.中海石油（中国）有限公司天津分公司，天津300452；3.中国石油西部钻探工程公司测井公司，新疆 克拉玛依834000）

0 引 言

复杂的井下环境与地层条件使阵列声波测井记录的地层信息以波场的形式叠加在一起。波场分离效果直接影响到信号提取准确程度，关系到后续处理与解释的可靠性。波场分离技术主要包括中值滤波、f－k滤波、拉东变换等处理方法。阵列声波测井波场分离主要采用速度偏移法［1］，f－k滤波、拉东变换等技术应用较少。速度偏移法需要已知声波时差与窗长，条件相对苛刻；中值滤波［2］用于分离直达波与反射波，不易分离上、下行反射波；f－k滤波对滤波器依赖较大，滤波器带通过窄，易出现Rieber现象［3－4］，而带通过宽则压制噪声效果变差；拉东变换存在假频与端点效应，应用效果受到限制。

本文采用频率域高分辨率拉东变换对阵列声波测井数据进行处理，克服了拉东变换过程中假频与端点效应的影响，确保信号不失真，同时采用双共轭梯度算法进行快速计算，提高了波场分离的精度与效率，使得该方法能够用于现场处理与解释。

1 高分辨率拉东变换原理

1.1 拉东变换

拉东变换将时间－深度域内的波场沿着不同斜率、不同截距进行数据叠加，得到斜率－截距（τ－p）域内的波场，对于具有不同同相轴的波场经过变换以不同形式分布在τ－p域内不同位置对τ－p域内分离的波场进行拾取，再反变换即可得到分离的波场，实现波场分离。

对于阵列声波测井纵波、横波和斯通利波3种模式波，不同振型的波列都包含直达波与上、下行反射波，其波场呈线性分布，同相轴倾斜代表不同模式波速度，截距代表直达波到时时间。经拉东变换，不同模式波均以点状分布在τ－p域内不同位置，直达波分布于p＝0的坐标轴不同位置；上行反射波分布于p＜0的不同区域位置；下行反射波分布于p＞0的不同区域位置。

对于阵列声波测井数据，拉东变换采用频率域离散形式［5］，有

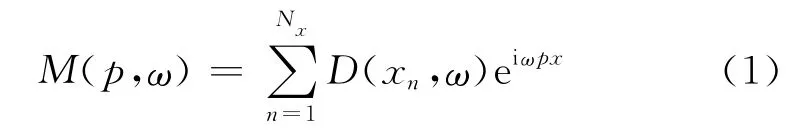
式中，M为模型空间；D为数据空间。式（1）通常写成矩阵形式，由于变换算子与其共轭转秩矩阵无法构成正反变换对，因此采用广义方法求取

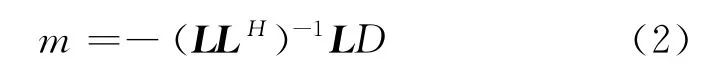
式中，L为变换算子，LH为L的共轭转秩矩阵。

为防止LHL计算时出现奇异矩阵或接近奇异矩阵，正变换过程中通常加入阻尼因子，得到最小二乘形式的稳定解［6］，有

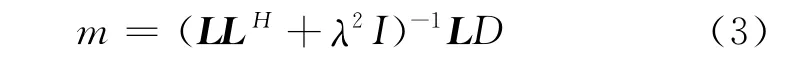
式中，λ为阻尼因子，取值为LHL最大特征值平方根的1%。

1.2 高分辨率拉东变换

拉东变换中阻尼因子为固定值，使得规则化矩阵恒定，降低了分辨率。高分辨率拉东变换在规则化矩阵中加入了与模型相关的先验信息，给出最小二乘变换的稀疏解，进而使得能量进一步集中，减少假频的产生。规则化方法根据Bayes原理使用非线性函数进行模型加权构建最小二乘的先验解，通过迭代方法实现，迭代过程中将上一次最小二乘解的误差作为重新加权的外部阻尼因子。

加权矩阵通过柯西类准则给出［7］

式中，Cm＝Wm）－1，W为模型空间加权矩阵，与模型m有关，通过上一次迭代结果对参数p的范围进行加权，达到提高分辨率效果。

通常模型空间呈稀疏分布，满足柯西分布的概率密度函数［8］，因此Cm为

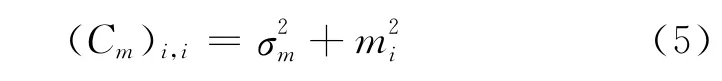
阵列声波测井数据所形成的矩阵为复对称正定矩阵，即Hermit矩阵，采用双共轭梯度算法［9］对其进行迭代求解。双共轭梯度沿着共轭方向搜索极值，对方程设定共轭初始搜索方向与步长，通过有限次的迭代得到所有解，大大提高计算速度。表1为不同算法对现场数据进行迭代求解所需要的时间对比表，从表1中可以看出，双共轭梯度算法计算效率最高。

表1 不同矩阵求解算法计算时间对比表

图1为模拟的不同同相轴反射波采用拉东变换与高分辨率拉东变换处理效果对比图。从图1可见，拉东变换能量相对发散，集中性较差，出现剪刀脚现象；而高分辨率拉东变换能量十分集中，以点状分布，分辨率明显高于拉东变换。

1.3 假频与端点效应

为了防止出现假频现象，高分辨率拉东变换参数p需要满足

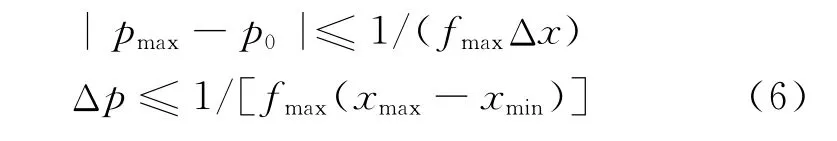
式中，pmax为最大斜率，s／m；p0为参考斜率，s／m；fmax为最大频率，Hz；Δx为相邻深度间隔，m；Δp为斜率采样间隔，s／m；xmax、xmin分别为最大、最小深度，m。

图1 拉东变换与高分辨率拉东变换效果对比图

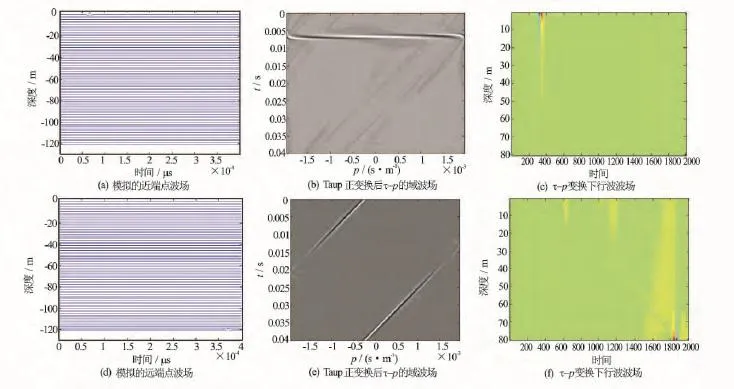
图2 理论模拟近端点与远端点波场拉东变换波场分离效果图

图2为理论模拟只包含近端点与远端点的下行波波场分别进行拉东变换以及分离后得到的下行反射波波场效果图。从图2上可以看出远、近端点在τ－p域内能量发散，整个p域内均有分布，分离出的波场严重失真，无法得到准确的下行波，出现端点效应。

图3为图1中理论模拟的上、下行反射波波场分别采用拉东变换与高分辨率拉东变换得到的波场分离效果图。图3（a）可以清楚地看出，拉东变换后的波场产生端点效应，而图3（b）高分辨率拉东变换由于能量高度集中，有效抑制了端点效应，分离效果更为理想，进一步验证了高分辨率拉东变换的可靠性与适用性。

2 高分辨率拉东变换技术应用效果

为了验证高分辨率拉东变换在阵列声波测井波场分离中的可靠性与实用性，对阵列声波测井波场进行了模拟。表2为模拟采用的主要参数，仪器从井底向上移动过程中声源不断发射，当模式波传播过程中遇到裂缝时产生反射，被仪器接收器接收，从而得到不同深度不同模式波的直达波与上、下行反射波，模拟忽略衰减及多次反射影响。经高分辨率τ－p变换上行反射波发现，上行反射波（见图4）能量明显集中且分布于p＜0区域，端点效应得到有效抑制，上、下行反射波波场分离效果明显，确保信号不失真。

图5为现场阵列声波测井数据分别采用拉东变换、f－k滤波、速度偏移、高分辨率拉东变换分离后得到的上、下行反射波波场。图5（a）为原始波场经过一维滤波与中值滤波处理后得到的斯通利波反射波；图5（b）为拉东变换分离后得到的上、下行反射波，端点效应明显；图5（c）为速度偏移处理结果，该方法通过最小二乘反演计算，因此波场幅度受到影响，且在直达波到达之前会出现轻微的伪反射波；图5（d）、图5（e）分别为扇形切割与扇形保留滤波器经f－k滤波后处理效果，扇形切割导致波场分离不彻底，只消除了切割部分的波场，扇形保留虽然只保留了目标波场，但出现Rieber现象；图5（f）为高分辨率拉东变换处理效果，端点效应得到很好抑制，信号不失真，能有效分离出上、下行反射波。

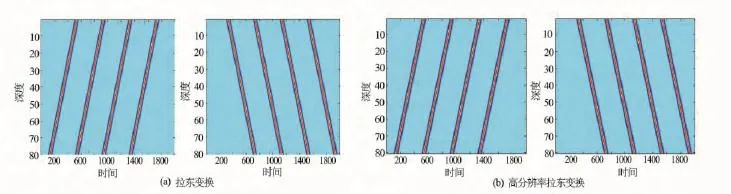
图3 高分辨率拉东变换与拉东变换波场分离效果对比

表2 阵列声波测井波场模拟参数表

图4 针对理论模拟的阵列声波测井全波进行的高分辨率拉东变换波场分离结果图

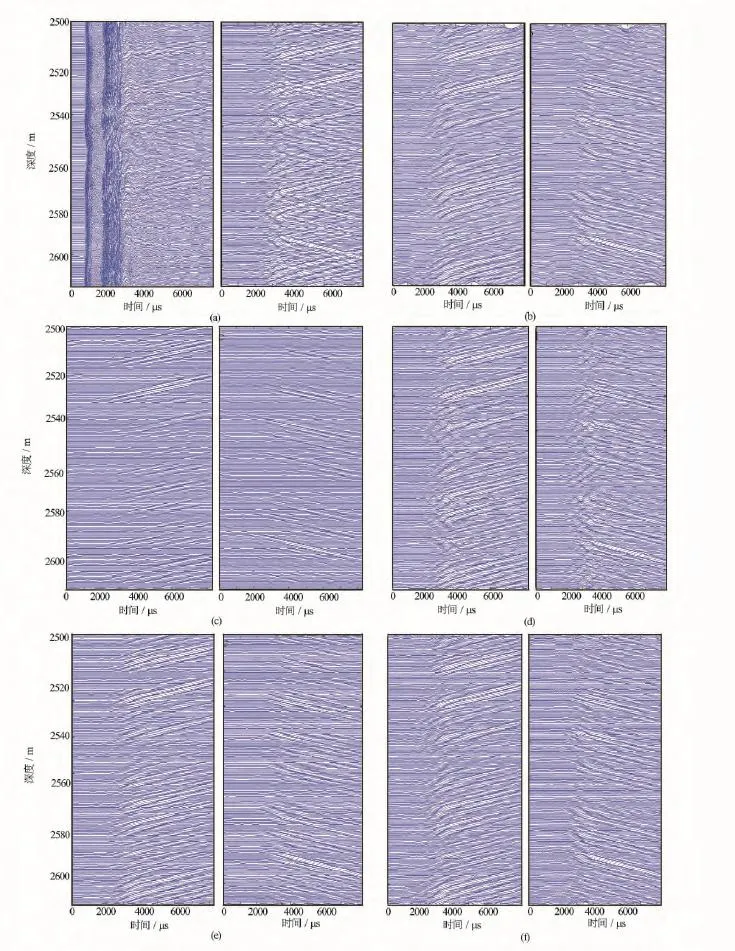
图5 不同波场分离方法分离效果对比图

3 结 论

（1）理论分析阐述了阵列声波测井高分辨率拉东变换原理，理论数据模拟证实该方法的可靠性。

（2）对比分析了不同波场分离方法对现场资料的处理效果。

（3）研究发现，不同波场分离方法均存在一定的优点与缺陷，高分辨率拉东变换有效解决了端点效应与假频问题，使得变换能量更为集中，相比拉东变换分辨率得到进一步提高；引入双共轭梯度算法，减少了反演计算时间，使得该方法能够用于现场处理，提高波场分离的精度。

［1］ 唐晓明，郑传汉.定量测井声学 ［M］.赵晓敏，译.北京：石油工业出版社，2004.

［2］ 唐金良，曹辉，王立华，等.中值滤波在井间地震资料处理中的应用 ［J］.石油物探，2005，44（1）：47－50.

［3］ 段云卿，朱广生，王彦春.VSP波场分离方法研究［J］.江汉石油学院学报，1991，13（3）：23－29.

［4］ Bob A Hardage.Vertical Seismic Profiling：Principles［M］.The University of Texas at Austin，Austin，Texas，USA.

［5］ Beylkin G.The Discrete Radon Transform ［J］.IEEE Transactions of Acoustics.Speech and Signal Processing，1987，35（2）：162－712.

［6］ Sacchi M D，Porsani M.Fast High－resolution Parabolic Radon Transform ［C］∥ Presented at the 69th Ann Mtg Soc Expl.Geophys，1999，Expanded Abstracts：1477－1480.

［7］ 王维红，首皓，刘洪，等.线性同相轴波场分离的高分辨率τ－p变换法 ［J］.地球物理学进展，2006，21（1）：74－78.

［8］ 刘喜武，刘洪，李幼铭.高分辨率Radon变换方法及其在地震信号处理中的应用 ［J］.地球物理学进展，2004，19（1）：8－15.

［9］ 张永杰，孙秦.大型稀疏复线性方程组双共轭梯度法［J］.航空计算技术，2006，36（4）：119－120.