提高低信噪比核磁共振测井弛豫信息真实性回波处理方法

王鹏，谭茂金，2

（1.中国地质大学地球物理与信息技术学院，北京100083；2.地下信息探测技术与仪器教育部重点实验室，北京100083）

0 引 言

核磁共振（NMR）测井回波信号（CPMG Echo Trains）的采集不可避免地要受到仪器设备和井下环境噪声的影响，记录到的回波信号带有很强的噪声，给反演解释工作带来极大的不确定性。当信噪比小于5时，直接反演便不能得出可靠的T2谱分布。Hansen等［1］针对噪声影响的强度给出了离散的Picard条件，说明当信噪比低于5时，回波信号与弛豫谱满足的第1类Fredholm积分方程所反映的模型已经完全不满足离散Picard条件，也就是说因为噪声的影响单从数学角度不能反演出真实可靠信息，必须对数据滤波或者重新采样［1－2］。

实际生产中，数据采集采用不同相位信号叠加，压制了很大一部分噪声，对于解释处理，叠加后的数据仍具有相当高的噪声。低信噪比核磁共振数据处理有翁爱华等［3］提出在反演中将基线偏移作为独立的参数参与反演，并结合时间依赖滤波技术提高了长弛豫信息反演的准确性。该方法将噪声影响合理地抽象成反演参数并参与反演与校正，但没能在小孔隙信息恢复上得到有效校正。Ma S等［4］提出了改进的分窗小波降噪方法，并与中值滤波、普通小波滤波和FIR滤波的降噪效果进行了对比，得出改进的分窗小波方法能够更好地提高带噪信号的信噪比，但在反演信息准确恢复上缺乏进一步验证。Ahmed O A W［5］提出了SLFT（Stable Linear Time－Frequence Transforms）方法，通过限制和平均变换系数实现了对分子药物核磁共振数据成像上的降噪。对于低磁场高噪声核磁共振测井数据，该方法目前仅具有借鉴意义。

本文针对低信噪比的核磁共振测井数据提出了基于奇异值分解法SVD（Singlar Value Decomposition）滤波的核磁共振数据变换反演方法BRD（Butler Reeds Dawson）。该方法利用Hankel矩阵与回波信号的相互构建关系，把回波信号的Hankel矩阵作为SVD滤波处理的信号矩阵，实现了对回波信号的分解和滤波。结合BRD反演算法，利用SVD处理后的高信噪比全波列数据反演出流体的T2分布。在随后的模拟数据试验和实际数据处理中，可以看到这样的分解和滤波在确保可动流体成分和提高束缚流体成分在反演信息准确恢复上是有效的。

1 处理方法与原理

整个数据的处理流程包括回波信号分解为高信噪比部分和低信噪比部分；低信噪比数据滤波；低、高信噪比数据反演；反演谱叠加。

1.1 回波信号分解

设核磁共振采集的回波信号为X，对应的T2谱为F。X可以分解为多项叠加的形式，如式（1）所示分解为X1和X2，相应的T2谱为F1和F2，与F的关系如式（2）所示，有

式（1）称为回波信号分解，这样的分解处理意义在于，对于低信噪比回波信号，回波信号的有效分解能够保证更多的有效信息与噪声信号分离，提高主要信息在反演处理中恢复的准确性。

图1（a）给出了含有100个样本的回波信号X，X分解为X1和X2的2个信号，它们之间满足式（1）。图1（b）给出了回波信号的T2谱，从左往右依次是X、X1和X2对应T2分布，它们之间的关系满足式（2）。

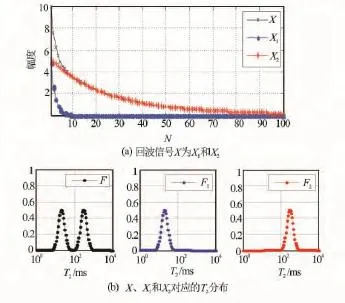
图1 回波信号分解

1.2 SVD滤波处理

1.2.1 滤波原理

对于一个m×n维信号矩阵A，对其进行SVD分解［6－7］，有

式中，U为m×m维正交矩阵；S为m×n维似对角矩阵；V为n×n维正交矩阵。当m＝n，S＝Σ；m＜n，S＝［Σm×mOm×（n－m）］；m＞n，S＝［Σn×n O（m－n）×n］T。Om×（n－m）是m×（n－m）维 零 矩 阵，O（m－n）×n是（m－n）×n维零矩阵。Σ＝diag（σ1，σ2，…，σp，…，σr）为非负对角矩阵，它的对角元素是由从大到小排列的奇异值构成。

通常，没有噪声的信号矩阵的秩很小，而含噪声的信号矩阵是一个满秩矩阵。受噪声的影响，原来排列靠后很小的奇异值会变得很大，SVD滤波原理就是将排列在某一奇异值之后所有奇异值置0，通过重构信号矩阵达到降噪的目的［8－9］。

为了描述置0奇异值分界点的选取，定义重构信号矩阵的能量比为

式中，p作为置0奇异值的分界点，奇异值σp以后的奇异值将被置0，输出信号占总能量比例为η。在实际处理中，为获取最优滤波信号，往往根据信号矩阵奇异值分布曲线的拐点选取p的位置，此时得到的能量比称为最优能量比。

1.2.2 信号矩阵

对于核磁共振回波数据X，它由N个等间隔采样点构成，表示为

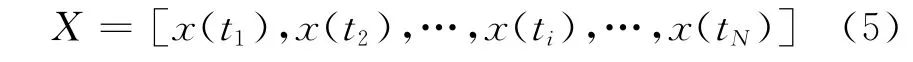
考虑噪声影响，令S表示期望信号，N0表示噪声，S和N0与X有相同的采样形式，式（5）可写为

根据回波信号与Hankel矩阵的构建关系［10］，令回波信号的Hankel矩阵作为反映该回波信息的矩阵，称为信号矩阵。回波信号X的信号矩阵H如式（7）所示，信号S和噪声N0也可以写出自己的信号矩阵，它们之间的关系H＝HS＋HN；HS和HN是S和N0对应的信号矩阵，有

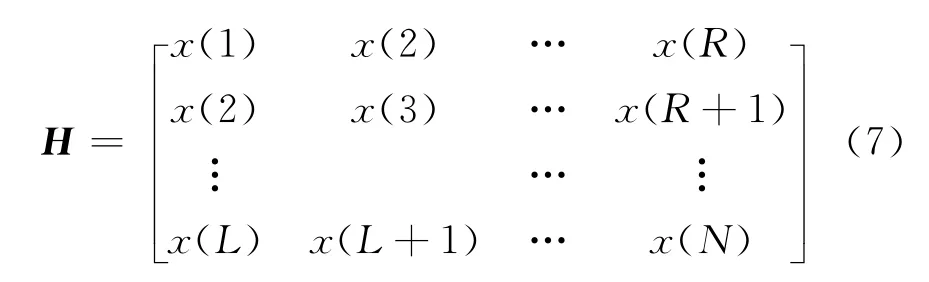
信号矩阵大小的选取应满足min（R，L）＞rank（H），对于数据大样本信号，构建信号矩阵应尽可能减少行或列的维数，以减少计算量。

信号矩阵通过式（8）计算可恢复相应回波信号

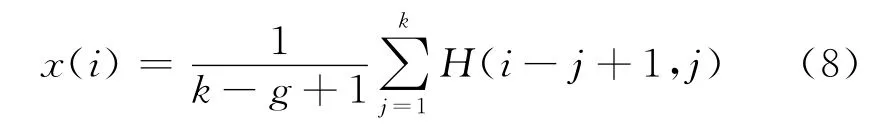
式中，g＝max（1，i－R＋1）；k＝min（i，N－R＋1）。

1.2.3 算法实现

回波信号的SVD滤波处理包含3个步骤。①构建信号矩阵，利用式（7）构建待处理回波信号的信号矩阵；②重构矩阵，根据滤波目的选择合适的能量比，得到降噪后的信号矩阵；③重构信号，由回波信号滤波后的矩阵经过式（8）得到重构信号，此时的重构信号即为经过SVD滤波处理后的回波信号。

1.3 反演弛豫信息

核磁共振测井依据地层流体在外加磁场作用下的弛豫特性反映地层流体孔隙度和区分地层中可动流体与束缚流体。根据核磁共振测井原理，从核磁共振测井采集的CPMG回波信号反演T2分布是典型的病态问题［2，11］，该问题被描述为式（9）及考虑噪声影响的离散形式（10），有

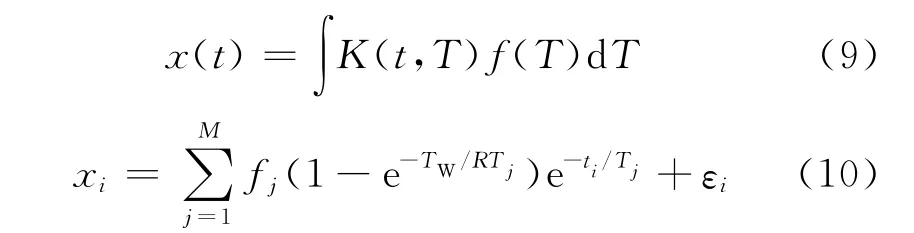
式中，xi为记录的第i个回波幅度的回波信号；ti（其中i＝1，2，…，N）为第i个相等回波间隔的衰减时间；Tj对应第j种流体的弛豫特性（其中j＝1，2，…，M），即弛豫时间T2；fj为第j种流体的T2幅度。TW为等待时间，R为T1／T2，方程（1）为第1类Fredholm方程。

测量信号xi不可避免地要受到噪声的影响。小的噪声干扰可能造成fj很大程度的不稳定，使得T2的分布强度fj不能有效、唯一地确定。目前提出的很多反演算法和正则化方法旨在抑制解的不稳定性和加强解的可靠性［12－15］，其中较为有效的算法是Venkataramanan等［13］提出BRD反演算法，该算法在目标方程中增加一项范数比例惩罚项抑制噪声影响。如目标方程（11）所示，方程中增加了带有平滑因子α的惩罚项

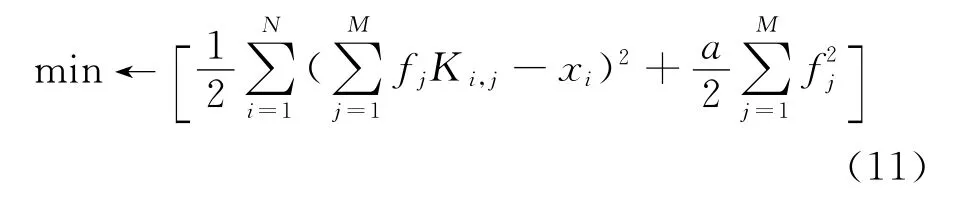
具体计算中，解的可行域范围内预设弛豫基确保解的合理性以及计算效率。例如，均匀分布在0.1～104ms范围内的30个离散值构成弛豫基。为方便起见，方程（12）给出了矩阵形式，待求参数为弛豫时间T2的分布强度向量F

1.4 处理流程

核磁共振测井采集的回波信号受噪声的影响主要表现，①在大、中孔隙可动流体成分造成基线偏移，在反演的弛豫谱上基线偏离表现为异常的长弛豫组分，这种影响在核磁数据信噪比较低时尤其明显；②在微、小孔隙束缚流体成分产生畸变，在反演的弛豫谱上表现为跳变的尖锐假峰。提高低信噪比回波信号反演弛豫信息的准确性，就是确保可动流体成分和提高束缚流体成分在反演信息准确恢复。

首先，应用SVD滤波高效的信噪分离能力进行回波信号分解，得到高信噪比的回波信号X1和低信噪比的回波信号X2，高信噪比的回波信号X1含有大量的T2弛豫信息可以直接反演得到相应的谱分布。其次，低信噪比的回波信号X2严重受到噪声影响，需要再次经过SVD滤波提取有用信息，然后反演得到相应谱分布。最后，根据回波信号分解关系，叠加2部分反演的T2谱作为最终要求取的T2分布。

反演数据的处理过程中2次用到SVD滤波。

（1）反演的回波信号经过SVD滤波实现回波信号的分解。SVD滤波算法采用低于最优能量比的设置，保证分解得到高信噪比数据X1。

（2）由回波信号分解理论，由X2＝X－X1计算得到相应的低信噪比回波信号X2。

（3）低信噪比数据X2的SVD滤波，提取有用信息。回波信号X2含有较高噪声，SVD滤波采用高于最优能量比的设置，保证有用信息不被丢失。

（4）回波信号反演。2部分经SVD滤波后的数据，反演得到相应T2分布、F2和F1。

（5）反演谱的叠加。由F＝F1＋F2计算回波信号X的T2分布、F。

2 方法验证与分析

根据邓克俊等［11］提出的 FCD（Fluid Component Decomposition）回波串构建弛豫信号的方法，取Gaussian函数作为基函数，高斯宽度（Full Width at Half Maximum）为0.9，考虑不同强度的噪声影响，正演得到不同信噪比的回波信号。对于含有束缚水和中等黏度油的双峰特征T2谱模型，束缚水的T2峰值在20ms处，峰值幅度为0.4，含水饱和度为40%；油的T2峰值在300ms处，峰值幅度0.6，含油饱和度60%；模拟采集间隔TE＝0.9ms，回波数N＝500；模拟得到的回波信号见图2。

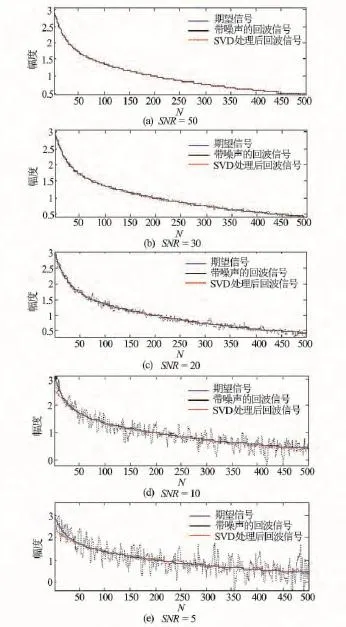
图2 模拟信号处理结果对比

图2中蓝色实线为没有加入噪声的回波信号，即期望信号，黑色点线为带噪声的回波信号，红色虚线为经过SVD滤波处理反演前2部分叠加的回波信号。图2（a）到图2（e）分别为信噪比50、30、20、10和5的带噪回波信号，相应的经过SVD滤波处理后的重构信号与期望信号。从中可以看出滤波后的信号有效地恢复到了期望信号，但随着信噪比下降过低时，SVD滤波处理仍旧保证了大弛豫成分信息的准确性，小弛豫信息会造成少量的丢失。

同时，反演了相应的弛豫谱。反演计算中，弛豫基分布区间0.3～3 000ms，布点数30（见图3），蓝色实线表示弛豫模型，黑色点实线表示带噪回波信号直接反演得到的弛豫谱（Fn），红色星实线表示经本文滤波处理得到的弛豫谱（F）。

如图3所示，应用本文方法处理得到的T2谱更接近模型，反演谱峰的位置与模型近乎一致。随着信噪比的降低，小弛豫成分峰值会有所丢失，但还是保证了弛豫位置的准确性；而直接反演得到T2谱只在油峰位置与模型相近，随着信噪比的降低，小弛豫位置会出现假峰。从对比的结果看，本文方法在低信噪比数据的处理上更接近真实情况。

图3 模拟信号处理结果对比

为定量说明反演效果，令反演得到的T2谱用列向量f表示，T2谱模型用列向量m表示，定义相对误差Er作为反演精度的度量，有

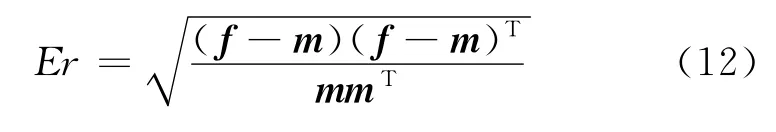
根据式（12），相应反演谱的相对误差见表1。由表1可知，随着回波信号信噪比的降低，直接反演方法得到谱分布的相对误差增加的很快，说明了当信噪比低或过低时，直接反演结果的不可靠性；与直接反演方法相比，在较低信噪比情况下，采用本文滤波反演方法得到谱的相对误差更小，误差变化幅度也更小。

当回波信号信噪比较高（SNR≥20）时，直接反演谱和经滤波反演谱的流体弛豫位置都与模型相一致，但滤波反演谱的整体相对误差要略大于直接反演结果，说明较高信噪比回波信号滤波处理时，由于信噪的分离难度加大，在设置滤除低强度噪声的同时，部分有用信息也被滤除了。因此，较高信噪比回波信号处理时应采用设置为全通能量的滤波反演模式或跳过滤波处理直接反演。

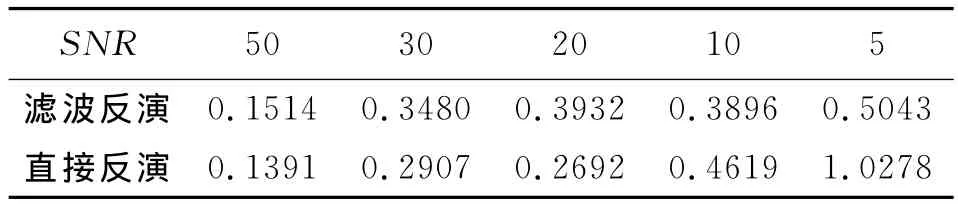
表1 反演谱相对误差

3 油田实例分析

某区×井核磁共振测井数据，测量仪器为MRIL－Prime，采用双TW测量模式识别可动流体，采集参数为，A组采用长磁化参数TW＝12.7s，B组采用短磁化参数TW＝2.0s，2组采用相同的采集间隔TE＝0.9ms和回波数NE＝500。2组回波信号的统计信噪比为，A组大约在2～19，B组大约在1～19，属于较低的信噪比数据。

图4为本文方法处理结果与商业软件DPP处理结果的对比图。图4中，第1道GR、SP；第2道为地层电阻率Rt、冲洗带电阻率Rxo；第3道为深度道；第4、5道为长TW，L和短TW，S回波信号的 DPP反演结果；第6道为DPP软件处理的长TW，L与短TW，S弛豫差谱；第7、8道为本文滤波反演方法处理的长TW，L和短TW，S结果；第9道为本文滤波反演方法处理的长TW，L与短TW，S弛豫差谱。可以看出，在××55～××73m深度段与DPP处理结果相比，在小弛豫位置弛豫谱没有出现噪声引起的跳变尖锐峰；在大弛豫位置压制了噪声引起的基线偏移造成的大弛豫成分；在A组和B组的弛豫谱上能够看到该层段存在大量的束缚流体和可动流体；从第6道和第9道的差谱信息上看，两者处理的差谱信号都很弱，但文中方法处理结果仍能看出可动流体中含有一定量的烃。

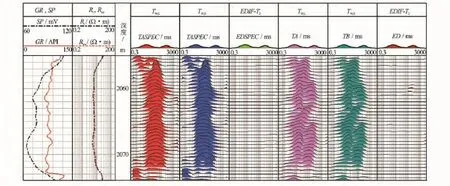
图4 实测数据处理结果对比

图5 岩性柱状图

图5为该层段录井岩性及含油级别测试结果。录井岩性显示，该层段岩性为深灰、灰黑色泥岩、灰色粉砂质泥岩与浅灰、灰褐色细砂岩呈略等厚互层，含油测试结果为油迹、油斑级别。该层段的测井响应资料显示，自然伽马曲线值为64.7～89.7API，均值为78.0API。三孔隙度曲线变化平缓，声波时差、密度均值分别为244.8μs／m、2.41g／cm3，中子16.8%～27.9%，说明地层孔隙发育，物性好。该层电阻率值略有变化，深感应电阻率值为5.0～15.0 Ω·m，均值为6.8Ω·m，阵列感应电阻率曲线明显分异，120in＊非法定计量单位，1ft＝12in＝0.304 8m，下同阵列感应电阻率值为4.9～14.9 Ω·m，孔隙度为13.8%，渗透率为0.62×10－3μm2，表明地层含油性较好，该层解释为油水同层。

4 结论与认识

（1）受噪声影响，核磁共振测井采集的回波信号表现为在大、中孔隙可动流体成分造成基线偏移，在微、小孔隙束缚流体成分产生畸变；在反演的弛豫谱上表现为异常的长弛豫和小弛豫位置跳变的尖锐假峰。尤其当信噪比低于5时，单从数学角度不能反演出真实可靠信息，必须对数据滤波或重新采样。

（2）提出基于SVD滤波的BRD反演处理方法，在低信噪比（SNR≤20）保证了可动流体和束缚流体信息在反演处理中的有效恢复，提高低信噪比核磁共振数据反演弛豫信息的准确性，在数值模拟和油田实例中都取得了令人满意的效果。从油田实例的应用效果看，与DPP处理结果相比，在小弛豫位置弛豫谱没有出现噪声引起的跳变尖锐峰，在大弛豫位置压制了噪声引起的基线偏移造成的大弛豫成分，在弛豫谱形态上能更精细地识别束缚流体和可动流体。

（3）SVD滤波处理利用Hankel矩阵与回波信号的相互构建关系，根据噪声强度选取适当的矩阵能量比压制和截断因噪声引起的奇异值的变化具有很强的信噪分离能力。

（4）实现了对回波信号的分解和滤波。在处理过程中，回波信号分解采用低于最优能量比的SVD滤波设置，保证信号分解的有效性和回波信号的反演精度，回波信号滤波采用高于最优能量比的SVD滤波设置，尽可能保留有效信息使之能够在反演中恢复。

［1］ Hansen P C.The Discrete Picard Condition for Discrete Ill－Posed Problems［J］.BIT Numerical Mathematics，1990，30（4）：658－672.

［2］ 肖立志，谢然红，廖广志.中国复杂油气藏核磁共振测井理论与方法 ［M］.北京：科学出版社，2012.

［3］ 翁爱华，李舟波，莫修文，等.低信噪比核磁共振测井资料的处理技术 ［J］.吉林大学学报：地球科学版，2003，33（2）：232－235.

［4］ MA S，KONG L，CHEN J.An Improved NMR Signal De－noising Algorithm Based on Wavelet Transform［J］.Computational Information Systems，2011，7（13）：4651－4659.

［5］ Ahmed O A W.Method for Removing Noise from Nuclear Magnetic Resonance Signals and Images：U.S.Patent 7，253，627［P］.2007－08－07.

［6］ Kalman D.A Singularly Valuable Decomposition：The SVD of a Matrix［C］∥College Math Journal，1996.

［7］ Aharon M，Elad M，Bruckstein A.SVD：An Algorithm for Designing Overcomplete Dictionaries for Sparse Representation［C］∥Signal Processing，IEEE Transactions，2006，54（11）：4311－4322.

［8］ Di F，Changzhi L，Qinguang C.SVD Filter Based on Noise Singular Values Clustering ［C］∥Intelligent Computation Technology and Automation （ICICTA），2010International Conference，IEEE，2010，3：665－668.

［9］ Sanliturk K Y，Cakar O.Noise Elimination from Measured Frequency Response Functions ［J］.Mechanical Systems and Signal Processing，2005，19（3）：615－631.

［10］ 刘志鹏，赵伟，陈小宏，等.局部频率域SVD压制随机噪声方法 ［J］.石油地球物理勘探，2012，47（2）：202－206.

［11］ 邓克俊，谢然红.核磁共振测井理论及应用 ［M］.东营：中国石油大学出版社，2010.

［12］ Butler J P，Reeds J A，Dawson S V.Estimating Solutions of the First Kind Integral Equations with Nonnegative Constraints and Optimal Smoothing［J］.SIAM Journal on Numerical Analysis，1981，18（3）：381－397.

［13］ Venkataramanan L，Song Y Q，Hurlimann M D.Solving Fredholm Integrals of the First Kind with Tensor Product Structure in 2and 2.5Dimensions［C］∥Signal Processing，IEEE Transactions，2002，50（5）：1017－1026.

［14］ LIAO G Z，XIAO L Z，XIE R H，et al.Influence Factors of Multi－exponential Inversion of NMR Relaxation Measurement in Porous Media ［J］.Chinese Journal of Geophysics，2007，50（3）：796－802.

［15］ Wang W，Li P，Ye C.Multi－exponential Inversions of Nuclear Magnetic Resonance Relaxation Signal［J］.Science in China Series A：Mathematics，2001，44（11）：1477－1484.