基于弹塑性理论的低压级组动叶叶根承载能力研究

骆天舒，林 炯

(杭州汽轮机股份有限公司，杭州 310022)

我们在分析最新设计的某低压级组动叶的叶根时发现，叶根及叶根槽危险圆角处的Von Misses 应力在转速为3 000 r/min 时几乎达到了材料的屈服极限，如果转速超出3 000 r/min，那么危险圆角处应力一定会超过屈服极限。这是因为离心力放大比例等于转速平方之比。目前杭州汽轮机股份有限公司(简称“杭汽”)是按照1.5 倍材料屈服极限取叶根及叶根槽强度极限，实际上已进入塑性区域。这点实际上与塑性力学理论［1］1利用材料在塑性区域内的承载能力是相符的，但缺乏在塑性区域内的定量计算，上述设计准则只是经验的。而且根据材料手册提供的屈服极限σs和强度极限σb，只能大致推测单轴塑性应力应变情况。本文所研究的是复杂的多轴弹塑性问题，所以采用非线性弹塑性有限元方法来研究这个问题。

1 理论模型

杭汽用来制造低压段转子和低压级组叶片的材料在实际温度不高的环境内(约100 ℃)，可以看作是与服从Mises 屈服条件的率无关的弹塑性材料。而且本文只考虑最危险的第一次加载过程，不考虑卸载，所以本文所用材料的应力与应变关系是一一对应关系，所研究的问题相当于一个非线性弹性力学问题。本文应用基于弹塑性增量理论［1］130的非线性有限元方法［2］来计算叶根和轮毂应力。弹塑性增量理论模型可以分为五个方面描述:应变分解关系、平衡方程、几何方程、本构关系、边界条件。

设已知物体在某时刻t 的位移场ui，应变场εij和应力场σij在物体V 内给定体力率，在边界ST上给定面力率并在边界Su上给定速度分布，要求出相应的速度场，应变率场及应力率场。以上变量需满足以下方程和边界条件:

1)分解关系:

2)平衡方程:

3)几何方程:

4)率无关本构方程:

式中:sij表示偏应力张量;表示偏塑性应变张量;由有限元软件用户从实验取得应力应变曲线数据输入。过去求解过该类问题采用的简单拉伸应力-应变关系是用两段直线表示的理想弹塑性模型或线性强化弹塑性模型。根据杭汽的实验数据及文献［3］可以知道，本研究应用材料之一2Cr13 的应力-应变关系(如图1 所示)很难用两段线性模型表示准确。所以本文根据杭汽理化实验室实验数据及文献［3 -4］确定了本研究所用材料的非线性本构关系，然后将本构模型用于有限元计算。

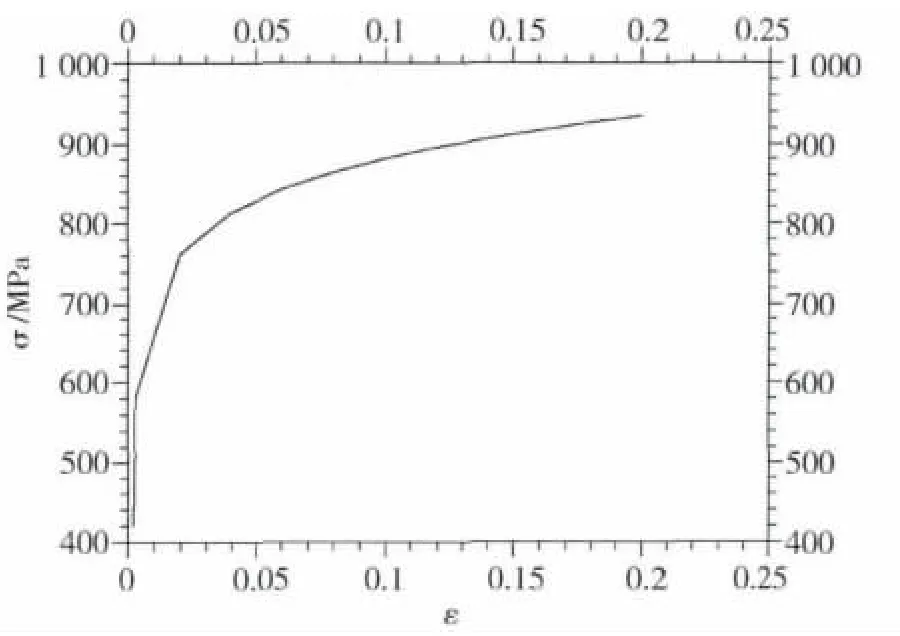
图1 2Cr13 本构单向拉伸应力应变关系

5)边界条件:

在推导有限元格式时，上述变化率量只要乘以Δt 就可以变成分段的增量，整个问题就可变成一个分段线性化的非线性弹性力学问题去求解。

2 算例

分析的叶片材料2Cr13 塑性区域特性见表1及图1。从图1 可以看到，2Cr13 显然是一种没有明显屈服阶段的材料。叶轮槽材料28CrMoNiv 塑性区域特性见表2。本文所分析的叶片和轮毂配合模型见图2。为简化起见，只取了一个扇区分析，在这个扇区两侧加了循环对称边界条件。在叶根和轮毂区域使用8 节点线性六面体非协调单元，在两者接触面使用了接触边界条件。

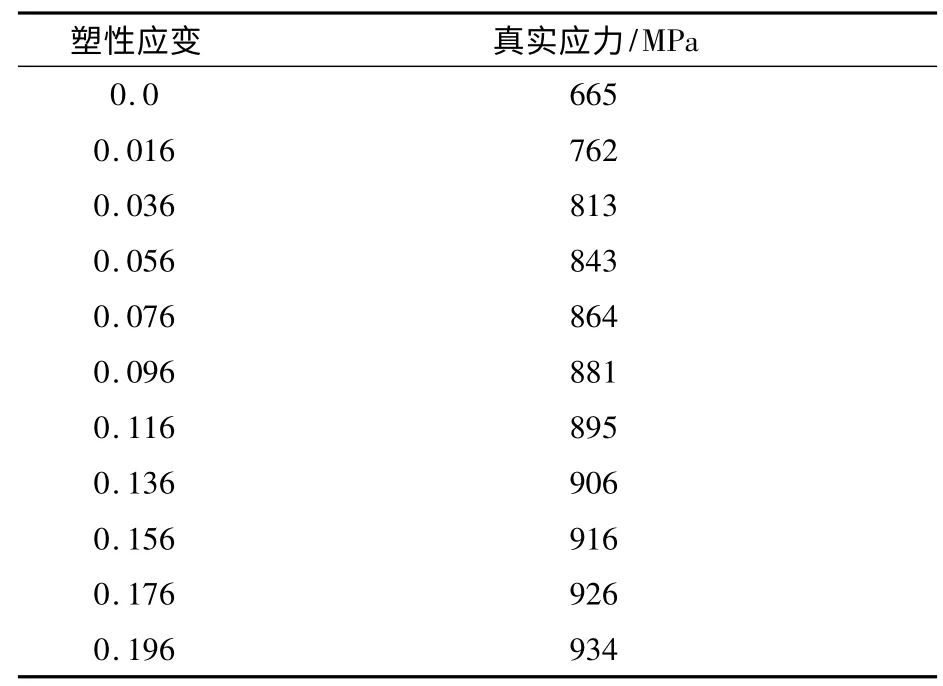
表1 2Cr13 应力应变关系数据

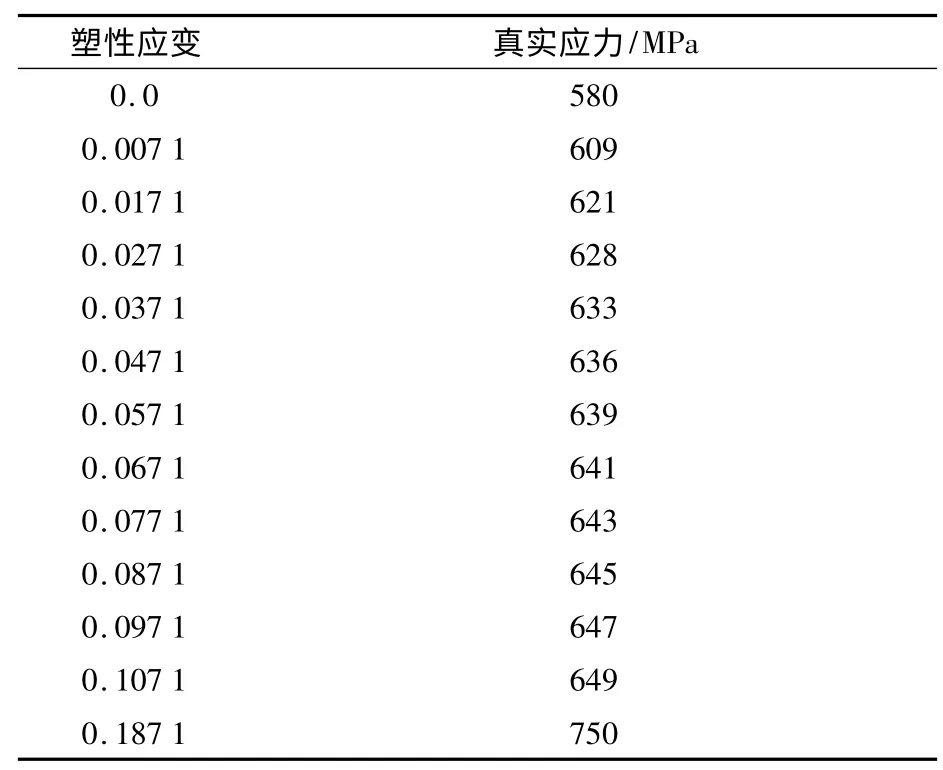
表2 28CrMoNiv 应力应变关系数据

图2 分析模型

在转速4 000 r/min 下，分别应用弹性力学有限元方法和弹塑性力学有限元方法求得了两组结果。其中弹性力学有限元方法的结果见图3、图4，弹塑性力学限元方法的结果见图5、图6。

图3 弹性力学有限元:叶根应力分布

图4 弹性力学有限元:叶根槽应力分布

图5 弹塑性力学有限元:叶根应力分布

图6 弹塑性力学有限元:叶根槽应力分布

从图3、4、5、6 上，我们可以得到如表3 所示的最大Von Mises 应力。表3 给出了两种方法的对比结果(忽略了有限元接触算法本身导致的接触边角处的应力奇异点)。

表3 最大Von Mises 应力(MPa)的比较

从表3 中可以看到，弹塑性力学有限元的计算结果远低于弹性力学有限元的计算结果。弹塑性力学有限元的结果计算显示，叶根及叶根槽大圆角处最大Von Mises 应力刚刚超过屈服极限，进入了塑性区域，远未达到强度极限。从材料的本构关系(图1、表1、2)来看，基于弹塑性理论算出的应力必然要低得多，从物理上来说更为真实。

3 结论

塑性力学理论［1］1认为物体从开始出现永久变形到最终破坏之间仍具有承受载荷能力。所以根据本文的两种数值计算结果可以得出结论:由于弹塑性力学有限元方法计算结果从物理上来说更为真实，弹塑性力学有限元方法的计算结果可以作为叶根及叶轮槽设计的重要的参考指标;根据塑性力学的理论及宗旨，利用弹塑性力学有限元方法的分析结果设计叶根及轮槽，可以更充分利用材料的承载能力。

［1］王仁，黄文彬.塑性力学引论［M］.北京:北京大学出版社，1992.

［2］BELYTSCHKO T.Nonlinear Finite Element for Continua and Structures［M］.New York:John Wiley ＆Sons Ltd.，2000.

［3］NOLKEMPER H M.Fliesskurven Metallischer Werkstoffe［C］//Hannover:Hannoversches Forschungsinstitute für Fertigungsfragen，1982.

［4］RIETH P.Zur Nachbildung der betriebsähnlichen Dehnwechselbeanspruchung massiver Bauteile aus warmfesten Stählen［D］.Darmstadt:TH Darmstadt，1982.