大功率汽轮机高温叶片蠕变特性数值研究
2014-12-03谢永慧常姣姣张明辉丰镇平
谢永慧,常姣姣,张明辉,张 荻,丰镇平
(西安交通大学能源与动力工程学院,西安 710049)
能源作为人类赖以生存和发展的物质基础,在经济和社会发展中有着举足轻重的地位。随着我国国民经济的快速发展,社会对能源的需求量不断增大。根据国家发改委对我国未来能源需求和结构的预测,到2050年我国一次能源需求量将增加到66.57 ×108t 标准煤[1]。在能源消费领域中,电力生产和消费占据非常重要的地位。中国富煤贫油少气的能源结构特点,决定了以煤为主导的电力生产方式在很长时间内不会发生变化。从对我国电力行业中装机容量的百分比预测中可以看出,在目前及今后10年中,以化石燃料为主的火力发电仍是我国电力能源供应的主要方式[2-3]。目前我们对化石能源的依赖仍很强,火力发电在电力行业中仍是重中之重。
无论从能源危机角度,还是从保护环境和防止全球气候变化角度考虑,提高化石能源转换效率,特别是提高电力生产效率,研究先进的发电设备已经成为从事能源设备研究和制造人员的一项迫切任务[4]。人类80%左右的电能是由汽轮发电机机组提供的,提高其效率对于节约能源和减少碳排放具有重要意义。
通常提高汽轮机机组的效率有两种途径:一是通过改善汽轮机的通流能力,减少能量损失来提高汽轮机的效率;二是从热力循环角度,改进汽轮机机组热力循环及提高汽轮机机组初参数并降低机组排气参数使机组效率得到提高。现代凝汽式汽轮机的背压一般为5~8 kPa,受环境条件限制,进一步降低排汽压力的空间已经不大。国内外都把提高汽轮机初参数作为进一步提高汽轮机机组效率的有效方向之一[5-6]。
随着汽轮机组朝着大功率、高参数方向快速发展,其进汽温度、压力都有了明显提高。金属材料机械性能在高温下会明显下降,高温条件下叶片的强度和蠕变特性成为大功率汽轮机部件强度考核的重点[7]。由于机组的工作温度很高,各部件所用材料的组织结构有所改变,晶体之间孔洞的生长会引起材料的蠕变破坏。众多学者的研究表明金属材料长时间的高温蠕变是影响其强度、导致其失效的重要原因。
汽轮机叶片在高温、高压、高转速及蒸汽环境等苛刻条件下工作,既要考虑气流激振引起的高周疲劳和在机组启停阶段引起的低周疲劳,又要考虑因高温引起的材料蠕变问题。当材料的温度达到其熔点的30%时就必须考虑蠕变问题[8]。为了保证汽轮机叶片和轮缘在恶劣的工况下安全工作,在研究大功率、高参数汽轮机的高温强度和寿命时,必须考虑高温蠕变等复杂的非线性力学问题。
Kachanov LM[8-10]等人提出不同的概念发展了连续损伤力学,以不可逆热力学和连续损伤力学作为基础,在材料的本构方程中加入损伤变量,使本构方程可以真实地描述材料损伤的宏观力学行为,并通过把纯疲劳损伤和纯蠕变损伤相加来研究疲劳-蠕变的交互作用。
为研究蠕变-疲劳的交互作用,Manson[11]等人提出了应变范围区分法(SRP 法),该方法把蠕变-疲劳循环中的非弹性应变分成4 种不同类型的分量并与其各自对应的寿命循环数相关联。这种方法的准确度取决于应变分量与其对应寿命循环数的函数关系及其加权函数的影响。
高温部件在实际运行过程中需要经受疲劳损伤和蠕变损伤,并存在交互作用,对两种损伤交互作用下的寿命预测得到广泛研究。把损伤累积过程看成是疲劳损伤和蠕变损伤线性叠加的线性累积损伤理论是最早的一种疲劳-蠕变寿命预测方法。该理论认为疲劳-蠕变共同作用下部件的寿命是疲劳损伤和蠕变损伤的简单叠加,未考虑蠕变-疲劳的交互作用。后来,国外学者Lagneborg R[12]等人通过在线性累积损伤理论中添加非线性的交互作用项来反映蠕变-疲劳的交互作用。
Karaivanov VG[13-14]等人采用有限元方法和计算流体动力学等方法计算了燃机叶片表面的温度分布和应力分布,并在此基础上计算了叶片的蠕变寿命,找到了叶片表面容易发生蠕变的敏感区域,并与已有的实验结果进行了对比,发现吻合得较好。
与此同时,国内学者北京航空航天大学的朱涛[15]等人针对某型航空发动机高压涡轮盘,用有限元程序计算该结构在循环载荷作用下的蠕变变形,并且考虑温度载荷的作用,计算了结构危险点在相应温度下的低周疲劳寿命及蠕变寿命,最后利用线性累积损伤理论进行涡轮盘结构的低周疲劳-蠕变寿命的预测分析。
为保证大功率汽轮机机组叶片的长期安全运行,本文以某汽轮机高温叶片为例,分析了高温蠕变对该叶片的影响,在此基础上,还研究了考虑气流力作用下叶片的静强度和蠕变特性。
1 蠕变计算理论
随着温度的升高,材料的力学性质会发生显著变化,所以对蠕变进行研究需要研究试件在外力作用下应力或应变与时间、温度之间的非线性关系。众多学者通过实验来观察材料应力与应变的变化规律,并建立蠕变计算理论,实现对部件寿命的评估。下面主要介绍蠕变计算的基本理论。
金属材料蠕变实验是使试件处于温度和应力恒定不变的状态,获得材料应变量ε 随时间t 变化的曲线,即蠕变曲线,材料的蠕变曲线分成三个阶段:不稳定蠕变阶段、稳定蠕变阶段和蠕变破坏阶段。材料处于不稳定蠕变阶段时,形变引起的材料硬化使蠕变速率不断降低,当蠕变速率减小到最小值时,试件进入稳定蠕变阶段,材料的变形强化与再结晶软化趋势达到平衡状态,蠕变速率基本维持恒定。在第三阶段即蠕变破坏阶段,试件发生颈缩和裂纹等破坏性损伤,蠕变速率迅速上升,直到试件发生断裂。
材料蠕变特性的另一个重要表现是应力松弛[16],应力松弛是指在恒温条件下试件的变形一定时,在蠕变试验中试件的应力会随时间不断减小。影响蠕变的因素非常多,包括材料因素、应力、温度等。要用统一公式总结出蠕变量εc、蠕变率与应力σ、温度T 和时间t 的关系非常困难,在蠕变研究的过程中人们通过某些假设,用较少的变量来建立蠕变理论,从而形成了以下几种主要的蠕变计算理论,包括:时间硬化理论、应变硬化理论、陈化理论、恒速理论理论等,以下进行简单介绍。
1.1 时间硬化理论
时间硬化理论把蠕变率表示成应力和时间的函数关系,来反映蠕变规律:

当描述应力松弛情况时,蠕变变形值不变,蠕变率为0,时间硬化理论由以下公式表示:

式中:σ(0)为初始时刻的应力,Pa;E 为材料的弹性模量,Pa。
时间硬化理论把时间看成是材料硬化的主要因素,未考虑蠕变变形的因素。
1.2 应变硬化理论
应变硬化理论把蠕变规律用应变,蠕变量和蠕变率三个变量来表示,常用的表达公式有以下两个:

式中:εc为蠕变应变;α、β、m、d、a、b 为与材料、温度等有关的试验常数。试验常数间存在如下关系:

分别对式(1)、(2)建立蠕变方程如下:
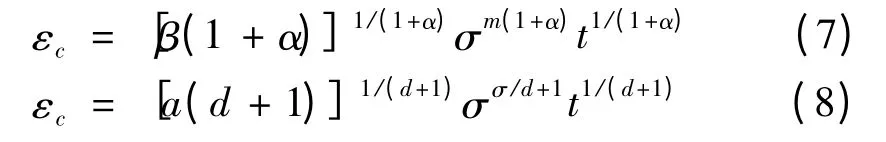
同理,对式(1)、(2)建立松弛情况下的蠕变方程如下:
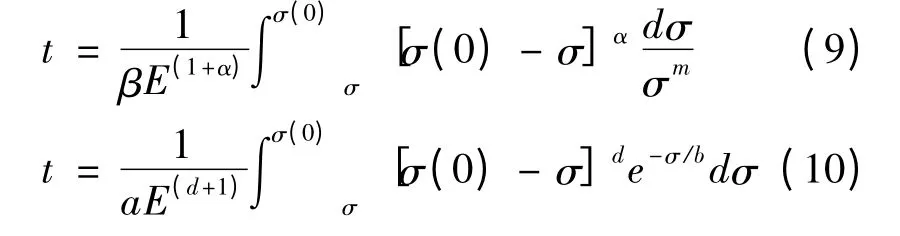
式中:σ(0)为初始时刻的应力值,其他参数含义同上。
对应变硬化理论的公式进行分析可知,当试件所受到的应力σ为常数时,蠕变率随蠕变量εc的增大而减小,蠕变率不可能为常数,因为蠕变量εc是不断变化的。所以应变硬化理论可以描述蠕变规律的第一个阶段,对于时间较短的蠕变规律的描述比较准确。
1.3 恒速理论

通常将符合上式的材料称为Norton 材料。当考虑瞬时弹性应变时,恒速理论则可用下式表示:

当用蠕变量来表示时,恒速理论在蠕变情况下表示为:

恒速理论在描述应力松弛情况时表示为:
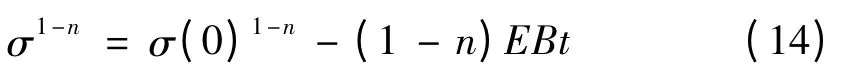
1.4 陈化理论
陈化理论把一定温度下材料的蠕变规律表示成应变ε、应力σ 和时间t 之间的关系。由于应变与应力和时间存在很强的非线性关系,陈化理论的常用公式为:

式中:A、m、n 为由试验决定的常数,与材料的种类、所受的温度等有关。其它参数含义同上。
在描述应力松弛情况时,陈化理论描述的蠕变规律可表示为:
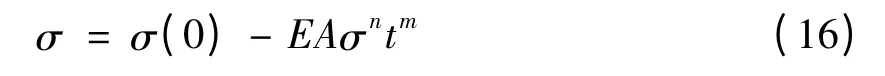
式中:σ(0)为试件在初始时刻所受到的应力,单位Pa,其它符号同前。
此外,陈化理论还可以表示成试件所受到的应力与应变及时间的关系。例如在描述应力松弛状况时,陈化理论下的蠕变规律可以表示成:

式中:C、a、b 为由试验决定的常数,与材料的种类、所受的温度等有关。其它参数含义同上。
由于陈化理论可较好地描述试件蠕变过程的第一、第二阶段[17],因此在工程中得到了较好的应用和发展。该理论模型已嵌入ANSYS 蠕变分析中,本文有限元计算所用即为此模型。
2 有限元模型
本文计算所采用的叶片模型为某大功率汽轮机高温叶片,叶身高度为34 mm,围带厚度为19 mm,叶片轴向宽度为80 mm,整圈为72 个叶片,模型如图1 所示。
图1 叶片与叶轮三维模型图
图2 为叶片与叶轮模型的网格示意图,除叶身与叶根平台之间的过渡区域采用四面体网格划分,模型其他区域均采用8 节点六面体单元进行网格划分。叶片模型节点总数为88 222,单元总数为28 272。叶轮部分全部为8 节点六面体网格,叶轮模型节点总数为62 220,单元总数为18 840。

图2 叶片与叶轮结构六面体网格图
3 考虑离心力和温度载荷的蠕变研究
3.1 载荷说明
对模型施加工作转速3 000 r/min 的离心力载荷,考虑到叶片处于工作状态时,叶片和叶轮各部分温度不均匀,将叶轮温度设为540 ℃,叶片工作温度分成两部分,叶根部位设为540 ℃,叶身和围带部位温度设定为598 ℃。
3.2 叶片热弹性计算结果分析
图3 给出的是叶片和叶轮模型总体位移图,叶片与叶轮结构总位移最大值为4.227 mm,位于围带部位。图4 为总体的等效应力分布,模型的等效应力最大值为246.8 MPa,分布于叶根部位和轮缘齿槽部位,叶片和叶轮上绝大部分区域应力在150 MPa 以下。

图3 叶片与叶轮总位移图(mm)

图4 叶片与叶轮等效应力图(MPa)
图5 为在离心力作用下轮缘的等效应力局部放大图,最大等效应力值为246.8 MPa,位于压力面轮缘第三齿圆角处。

图5 轮缘应力放大图(MPa)
图6 显示叶片上最大等效应力值为228.5 MPa,位于叶根压力面第三齿圆角处。

图6 叶片等效应力图(MPa)
前面分别给出了叶片在离心力和温度载荷共同作用下的总体位移和应力状况。这部分计算结果可以为蠕变分析提供基本参数。
3.3 叶片蠕变计算结果分析
本文共计算了100 000 h 蠕变,图7 为叶片与叶轮100 000 h 蠕变时的总位移图,从图中可得,叶片与叶轮结构总位移最大值为4.282 mm,位于叶片围带顶部。

图7 叶片与叶轮总位移图(mm)
图8 为叶片与叶轮100 000 h 蠕变时的等效应力分布,由图中可得,叶片与叶轮结构的最大等效应力值为222.5 MPa,应力最大值的位置需在叶片和叶轮分开的应力图中查看,叶片与叶轮上绝大部分区域应力都在120 MPa 以下,整个结构应力水平不高。图9 为轮缘局部放大图,最大等效应力值为222.5 MPa,位于轮缘压力面第三齿的圆角处。图10 为叶片100 000 h 蠕变作用的总位移分布图。从图中可知叶片的总位移最大值为4.282 mm,分布于压力面一侧的围带顶端部位。由图11 叶片100 000 h 蠕变作用的等效应力分布可知,其等效应力最大值为197.9 MPa,位于叶根压力面的第三齿圆角处。

图8 叶片与叶轮蠕变等效应力图(MPa)

图9 轮缘应力放大图(MPa)

图10 蠕变作用下叶片总位移图(mm)
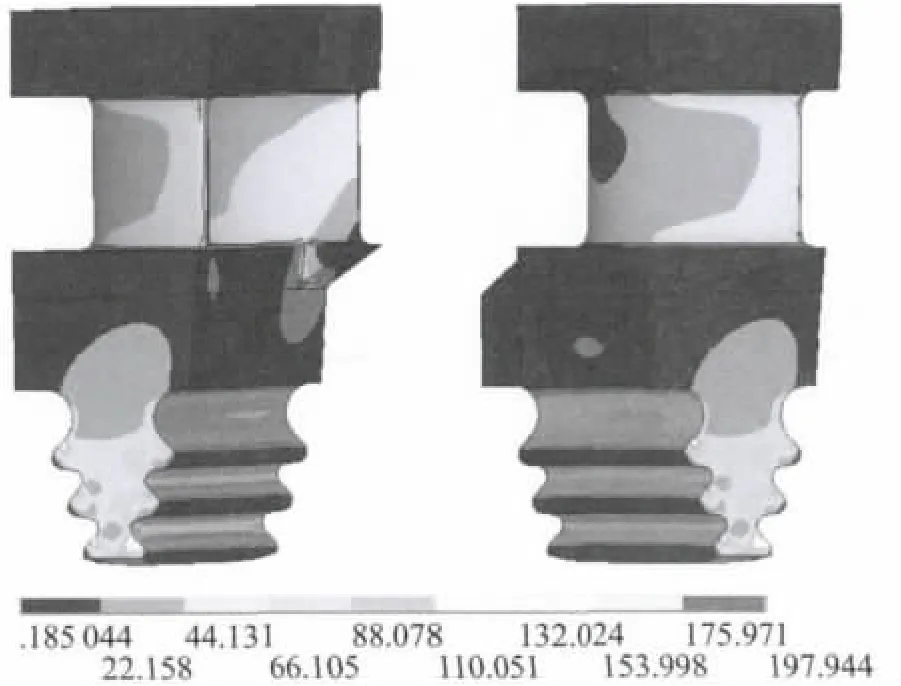
图11 蠕变作用下叶片等效应力图(MPa)
由前面分析可知,叶片热弹性最大位移量是4.227 mm,最大等效应力为246.8 MPa,最大径向位移量为4.209 mm。而叶片与叶轮在100 000 h下蠕变作用的最大位移量为4.282 mm,对应的最大等效应力值为222.5 MPa,最大径向位移量为4.257 mm。由此可得叶片与叶轮总的蠕变伸长量为0.055 mm,径向(叶高方向)蠕变伸长量为0.048 mm,等效应力降低了24.3 MPa,应力松弛明显。图12、图13 和图14 分别给出了蠕变效应下的变形、应变量和应力随时间变化的曲线图。
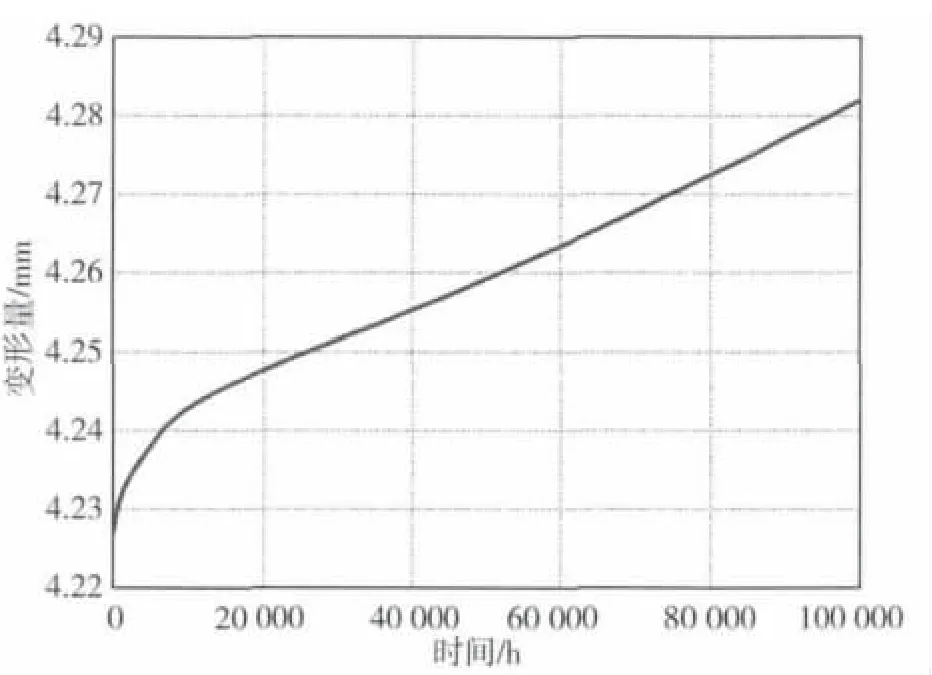
图12 叶片与叶轮最大位移随时间变化曲线

图13 叶片与叶轮最大应变量随时间变化曲线

图14 叶片与叶轮最大应力值随时间变化曲线
4 结论
1)本文基于蠕变分析的基本理论,建立了采用有限元方法进行蠕变分析的研究思路及方法,并以某汽轮机高温叶片为例,构造叶片与叶轮结构的三维模型,采用有限元分析软件ANSYS 分析叶片在离心力和温度场作用下的热弹性应力应变,进一步计算了叶片与叶轮经历100 000 h 蠕变历程的应力和变形量;
2)由于在运行工况下汽轮机叶片温度较高,由温度引起的热膨胀即热弹性作用较明显,对叶片应力和变形均有较大影响,尤其是会使叶根齿面承载分布很不均匀。所以在进行大功率汽轮机机组高温叶片强度分析时,需要将温度因素引入分析求解中,充分考虑热弹性的作用;
3)由叶片与叶轮模型最大等效应力点的应力随时间变化曲线可以看出,经历了100 000 h 之后,该部位应力降低了24.3 MPa,比初始时刻降低了10%,应力松弛程度较明显。
[1]许红星.我国能源利用现状与对策[J].中外能源,2010,15(1):3-13.
[2]吴敬儒,邱言文.确保国内生产总值翻两番的2001-2020年电力工业发展研究[J].电网技术,2003,27(4):1-6.
[3]王家诚.合理开发利用能源应对全球气候变化[J].当代石油石化,2009,17(10):1-8.
[4]张素心,阳虹,姚祖安.超临界汽轮机的开发与展望[J].上海汽轮机,2002(1):15-22.
[5]黄瓯,阳虹,彭泽瑛.我国超超临界汽轮机的发展方向[J].热力透平,2004,33(1):1-7.
[6]唐飞,董斌,赵敏.超超临界机组在我国的发展及应用[J].电力建设,2010,31(1):80-82.
[7]张红梅.超超临界汽轮机高温叶片强度分析[D].上海:上海交通大学,2011.
[8]KACHANOV L M.Time of the Rupture Process Under Creep Conditions[J].USSR Division of Engineering Science,1958,8(1):26-31.
[9]ROBOTNOV Y N.Creep Problems in Structural Members[M].Amsterdam:North-Holland Publishing Company,1969.
[10]LEMAITRE J.How to Use Damage Mechanics[J].Nuclear Engineering and Design,1984,80(2):233-245.
[11]MANSON S S,HALFORD G R,HIRSCHBERG M H.Creep-Fatigue Analysis by Strain-Range Partitioning [C]//First Symposia on Design for Elevated Temperature Environment.USA:ASME,1971:2-28.
[12]LAGNEBORG R,ATTRMO R.The Effect of Combined Low-Cycle Fatigue and Creep on the Life of Austenitic Stainless Steels[J].Metal Trans.,1971,2(7):1821-1827.
[13]KARAIVANOV VG,MAZZOTTA DW,CHYU MK,et al.Three-Dimensional Modeling of Creep Damage in Airfoils for Advanced Turbine Systems[C]//Power for Land,Sea,and Air.Germany:ASME,2008:9-13.
[14]VENTZISLAV G Karaivanov,DANNY W Mazzotta,MINKING K Chyu,et al.Three Dimensional Modeling of Creep Damage in Airfoils for Advanced Turbine Systems[C]//Proceedings of ASME Turbo Expo 2008.Berlin,Germany:Gas Turbine Technical Congress and Exposition,2008:GT2008-51278.
[15]朱涛,胡殿印,王荣桥.航空发动机涡轮盘低周疲劳-蠕变寿命预测[J].科技创新导报,2008,25(9):84-85.
[16]穆霞英.蠕变力学[M].西安:西安交通大学出版社,1990:5-6.
[17]胡柳欣.600MW 汽轮机隔板蠕变寿命评估方法研究[D].上海:上海交通大学,2009:1.
