汽轮机低压外缸强度分析中的自由度耦合方法

2014-12-03邓志成史进渊

热力透平 2014年1期

汪勇，杨宇，邓志成，史进渊

(上海发电设备成套设计研究院，上海 200240)

汽轮机低压外缸的主结构一般由钢板、钢块和钢管等焊接而成。低压外缸的强度和屈曲是结构安全性设计重点关心的内容［1］。在计算机技术尚不发达的过去，一般通过简化的理论公式计算或通过有机玻璃模型试验来评估汽缸的强度和屈曲性能［2］。随着计算机的不断发展，近二三十年来，数值计算方法被广泛应用于汽轮机低压外缸的强度和屈曲计算中［3-4］。为了进行强度及屈曲的有限元分析，通常将钢板简化为片体用壳单元离散，将钢管简化为线体用梁单元离散，将钢块直接使用实体单元离散。由于实体单元、壳单元和梁单元三类单元节点分别具有不同的自由度，在有限元计算时需要考虑彼此的节点自由度耦合问题［5-6］。

本文通过数值试验方法，将不同类型单元连接的模型与全实体模型的计算结果进行对比，证明了这些处理的合理性，然后将这些处理方法应用于汽轮机外缸的强度及屈曲分析中。

1 不同单元的节点自由度

在结构计算中，三维实体单元、空间壳单元和空间梁单元三类单元的自由度情况为:

实体单元节点有三个自由度，分别为ux、uy和uz，其单元的节点只具有三个方向的平动自由度，空间旋转通过节点位置的相对转动来表现。

壳单元节点有六个自由度，分别为ux、uy、uz、θx、θy和θz。壳单元的节点具有三个方向平动和三个方向的转动自由度。在线弹性板壳理论的基本假设当中，θz自由度不能通过直接求解平衡方程得到，而是通过节点在中面内的相对位置转动来表现。为了避免由于平衡方程线性相关而导致计算结果不是唯一的，同时也为了方便计算程序的编制和前后处理，在程序中，人为引入了描述θz方向刚度的非零刚度系数Kθz。尽管引入Kθz不会影响到其它自由度的计算结果，但由于壳单元的θz自由度计算结果与Kθz直接相关，程序直接输出的节点θz结果是不真实的。

梁单元节点有三个平动和三个转动自由度，即ux、uy、uz、θx、θy和θz。与壳单元不同，梁单元的六个自由度都是由平衡方程直接求解得到的。当梁单元与壳单元仅仅共点连接时，两种单元之间在壳单元θz方向的力矩将无法正确地传递，直接影响到位移、应力及振动特性的计算结果。

2 不同单元节点的自由度耦合

由于三类单元的节点自由度各不相同，若只是简单地共用连接处不同类型单元的节点，必然导致缺失的节点自由度无法正确传递。为解决这个问题，在不同自由度的单元节点之间引入多点约束方程(MPC)。MPC 通过引入连接部位附近的其它计算节点，根据物理实际加入变形协调条件，弥补单元本身自由度的不匹配。本文使用MPC 方法来设置不同自由度的单元节点间的连接，根据连接部位具体的情况不同，采用不同的方法。

2.1 梁单元与壳单元附着连接

梁单元与壳单元附着连接是指壳体上有加强筋、加强梁、加强杆或者是杆板连接时存在过渡片的情况(如图1 所示)。

经过简化的壳体与线体之间的公共部分是一条线而不是一个点。这些公共线在有限元离散时至少含有两个以上的节点和一个以上单元的边。为保证计算精度，模型处理时要保证两类单元间有三个以上的节点和两个以上单元的边共用。这样，壳单元的θz自由度可以自然地由公共点在平面内的相对移动实现与梁单元相互传递。在梁单元与壳单元附着连接的情况下，只要两类单元在连接部位共用节点，便达到了自由度耦合的效果。

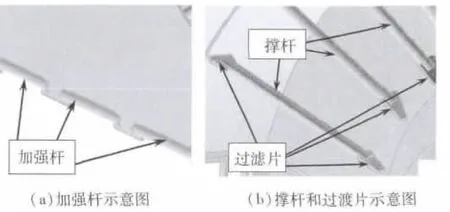
图1 梁单元与壳单元附着连接示意图

2.2 梁单元与壳单元正交或斜交连接

当支撑杆与壳体呈正交或斜交(如图2 所示)连接时。撑杆经简化后成为线体，壳体经简化后成为片体，两者正交或斜交时的交集是一个点。在这种情况下，有限元离散得到的壳单元与梁单元只有一个公共节点连接，梁单元在壳单元θz方向的旋转将无法正确计算。使用MPC 方法将两者进行连接，将空心撑杆的中面沿杆长方向投影到壳体中面，将投影得到的圆或椭圆上的节点(从节点)与撑杆简化得到的梁单元连接端点(主节点)进行MPC 连接。如此，壳单元连接部位的θz自由度由MPC 从节点的彼此相对旋转来计算，实现了梁单元和壳单元节点间的自由度耦合。

图2 杆与板(或实体)正交和斜交示意图

2.3 梁单元与实体单元正交或斜交连接

当支撑杆与实体相互呈正交或斜交(如图2所示)连接时，如不进行特殊处理，则梁单元与实体单元仅共用一个节点。由于实体单元的节点没有转动自由度，梁单元与实体单元呈三维铰接状态，无法呈现杆与体之间的焊接特征，将降低模型的刚度。这种情况的处理方法与梁单元和壳单元的正(斜)交连接类似。将空心撑杆的中面沿杆长方向投影到实体表面，将投影得到的圆(斜交时为椭圆)上的节点与梁单元的主节点进行MPC连接。通过MPC 从节点的协调变形，将杆单元节点上的三个旋转自由度传递给实体单元，实现空间梁单元与三维实体单元间的自由度耦合。

2.4 壳单元与实体单元的连接

当壳单元与实体单元连接时，如仅让连接部位壳单元轮廓上的单元与实体单元共用节点，则两类单元表现出一维铰接的特点，两类单元仍然能够在围绕单元的边长方向彼此旋转，将降低有限元模型的整体刚度。为解决这个问题，分以下4 步进行壳单元与实体单元的MPC 连接。

1)在壳体与实体连接的部位，分别用壳体的上面、中面和下面切开连接的实体表面。

2)将剖切后实体表面的三条线与对应的壳体中面轮廓线用相同数量的节点进行剖分，且每一组对应的四个节点分布在中面的同一条法线上。

3)将壳单元轮廓上的节点与相同空间位置的实体单元节点合并为一个节点(即共用节点)。

4)依次将壳单元轮廓上的各个节点作为MPC 主节点与共法线的另外两个剖线上的实体单元节点进行MPC 连接。

其中，第3 步保证空间壳单元与三维实体单元节点之间的平动自由度耦合，第4 步实现了两类单元之间转动自由度的耦合。

三类单元连接的有限元模型示意如图3 所示。

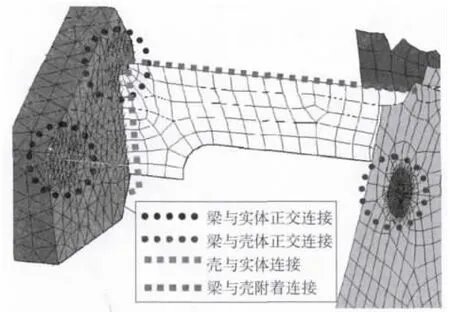
图3 三类单元连接示意图

2.5 不同类型单元的连接方式小结

在本文建立的汽轮机外缸模型中，梁单元与壳单元、壳单元与实体单元、实体单元与梁单元的节点之间都使用了多点约束方程(MPC)的连接，建立了符合工程实际及求解所需要的三维有限元计算模型。当梁单元附着在壳单元之上时，使用了共节点方法进行自由度耦合。文中使用到的各类单元节点间的自由度耦合方法示意如图4 所示。

图4 三种不同的单元之间的连接方式

3 连接方法的验证

上面介绍了不同自由度单元之间的连接方法。这里对几种连接方法进行数值试验验证，即将不同单元的连接模型计算结果与全实体单元模型的计算结果进行比较，以验证处理方法的正确性。

3.1 梁单元与壳单元的连接

为验证梁单元与壳单元在正交或斜交连接中使用MPC 连接方法处理的正确性，本文建立了如图5 所示的数值试验几何模型，并将该几何模型简化为如图6 所示的梁－壳模型和全实体模型这两种模型。

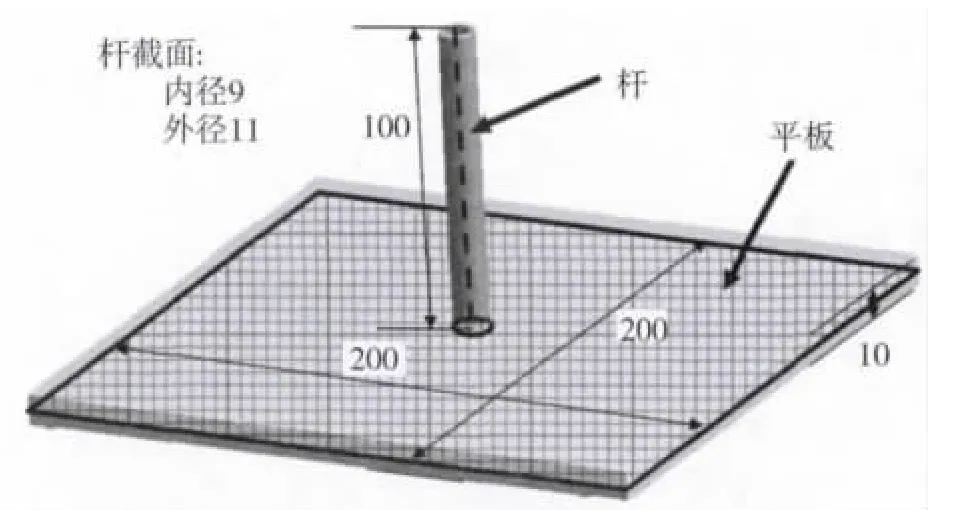
图5 梁与壳体连接的数值试验几何模型/mm

在图6 所示的梁－壳模型中，平板被简化为壳单元，而杆被简化成梁单元;在全实体模型中，杆和平板均使用实体单元。为验证壳单元节点的θz自由度与梁单元节点之间耦合处理的正确性，在杆的自由端施加围绕杆轴的200 N·m 的扭矩。每个模型均约束四边形平板的三个角点，两个模型的力学边界如图6 所示。

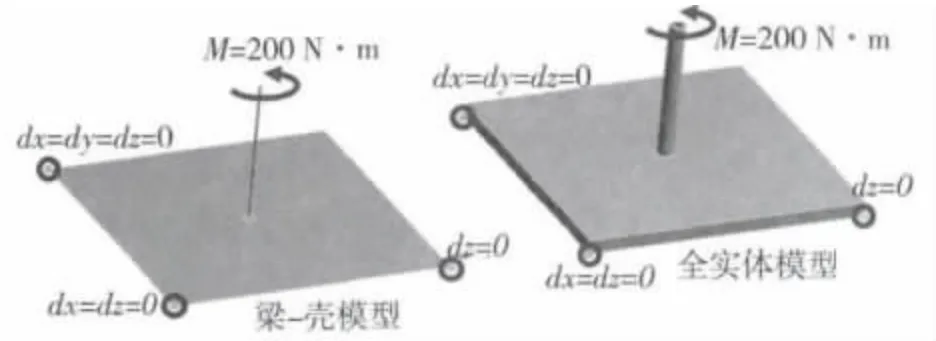
图6 梁与壳体连接的数值试验的力学边界

试算中使用的材料弹性模量E=200 GPa，泊松比为0.3。经过剖分后两个试验模型的网格如图7 所示。

图7 梁与壳体连接数值试验的网格

两个模型计算得到的杆绕其轴的转动位移结果如图8 所示。梁与壳连接的数值试验和不同模型的计算结果偏差列于表1，两种模型的旋转位移偏差仅为3.75%，表明本文对梁与壳连接的处理方法是合理的。

图8 梁与壳体连接数值试验的位移放大图

表1 梁与壳连接试验模型的计算结果

3.2 实体单元与壳单元的连接

为了验证壳单元与实体单元连接时的计算精度，本文建立了如图9 所示的数值试验几何模型。图中的薄壳部分在有限元模型中用壳单元和实体单元分别进行试算，结果相互比较以说明壳单元与实体单元连接方法的正确性。

图9 壳与实体连接的数值试验几何模型/mm

在图9 所示的几何模型上，壳体部分施加1 MPa的法向压力，固体另一端面完全约束。其力学边界的示意如图6 所示。在壳体与实体连接的部位，使用上文中提到的方法进行连接。

对模型进行有限元离散、边界处理和计算后，得到图10 所示的挠度计算结果。试算中使用的材料弹性模量E=200 GPa，泊松比为0.3。壳体部分端面(端线)的位移列于表2。

图10 壳与实体连接的数值试验挠度结果

表2 壳与实体连接试验模型的计算结果

壳－实体和全实体两种模型的挠度值计算结果偏差仅为0.243%，表明了本文处理壳与实体连接方法的合理性。

3.3 不同连接方法的结果验证分析

对不同类型单元节点自由度耦合的连接方法进行了验证。对不同单元节点自由度耦合建模和全实体单元建模分别进行有限元分析，由表1 和表2 结果对比表明，彼此之间的偏差在5%以内，证实了这些处理方法的正确性。

4 汽轮机低压外缸计算模型

根据汽轮机低压外缸三维实体模型，使用两种思路进行简化，得到了由片体、线体构成的模型I 和由实体、片体和线体共同构成的模型II 分别用于构建三维有限元离散模型。对于模型简化得到的实体、片体和线体，分别使用了实体单元、壳单元和梁单元进行离散。两种几何模型简化方法、各类几何体使用的单元和简化流程如图11 所示。

根据图11 流程，得到模型I 和模型II 两种有限元计算模型，其中模型I 没有使用实体单元;模型II 为了更接近实际设计情况，该模型适当引入了实体模型。