基于地基投影的建筑场景立面建模
2014-12-02任新宇李郁峰段晶晶
任新宇,范 勇,李郁峰,段晶晶,刘 旭
(西南科技大学计算机科学与技术学院,四川 绵阳621010)
1 概述
多视图建筑场景建模作为基于图像的三维建模研究热点之一,仅依靠相机从多个视点拍摄室外建筑场景的多幅图像,即可恢复该场景建筑逼真的三维模型。该方法所需设备简单、易于操作,其重建结果被广泛应用于数字化城市规划、智能场景监控、机器人导航、虚拟现实等领域,特别是对街道等场景建筑体的垂立外侧面(立面)的建模[1-2]。
多视图建筑场景建模的一般方法是,通过特征检测搜索稀疏的图像特征点,再由视图序列的特征点匹配完成摄像机标定,最终恢复这些稀疏点的空间三维坐标[3]。目前,该方法应用于立面建模时,以分割后的立面为重建目标构建模型,但均限于特征点的有效覆盖规模,所恢复的三维点云并不能大面积地表示视图立面,即只完成图像的稀疏重建。有的通过三角面片来填补特征点间没有重建的可见点,但插值误差较大,填补点在透视层次上的远近深度正确率低[4];有的通过人工规定特殊点计算矫正立面,不仅特殊点选择苛刻,而且构建立面局限于单方向立面的纹理形状矫正,如仅恢复沿街方向的建筑立面等[5-6];有的在一般方法上引入面扫描来增加稠密点,但扫描方向计算困难,需要惯性导航系统(Inertial Navigation System,INS)、全球定位系统(Global Positioning System,GPS)等辅助设备,稠密点重建精度不高[7]。这些立面建模的方法未能充分利用三维稀疏点的空间结构信息,且对多方向纹理立面的重建误差较大,设备成本高、要求严格,系统庞大。
针对此问题,本文提出一种利用地基投影法进行建筑场景立面建模的新方法。该方法计算稀疏点并以此同时完成地基线计算和立面矫正,充分利用地基线方位信息完成立面生长与模型融合。
2 地基投影法
地基线在建筑学中被用于表示建筑体的俯视轮廓和外墙体方位。本文将其引入视觉重建,主要用以计算建筑立面的地理布局,同时提供场景空间扩展的方位延伸关系。计算出场景地基线与矫正立面后,为矫正立面赋予其所在地基线的方位信息,可快速、高效地建立场景建筑的立面模型。以普通数码相机围绕建筑场景拍摄的图像序列为输入数据,要求拍摄目标清晰可见。利用地基投影法的建模算法流程如图1 所示。
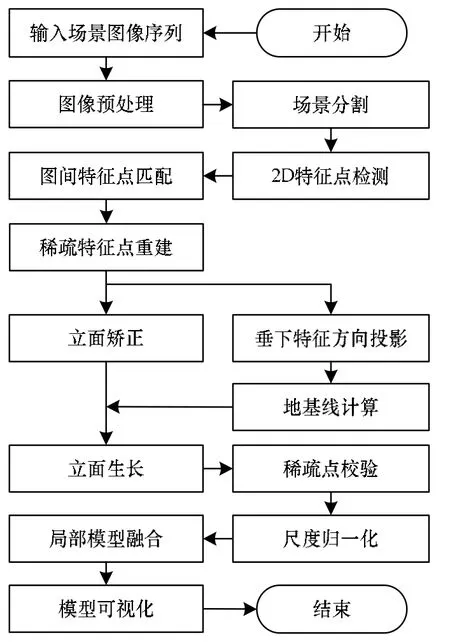
图1 利用地基投影法的建模算法流程
2.1 场景预处理
原始图像序列存在不利于特征识别的噪声,需首先进行图像预处理,以获得几何、纹理特征清晰的图像。本文采用平滑滤波与轮廓增强[8]的预处理方法,图2 为原图添加5%高斯噪声后的建筑场景图像及其预处理结果。

图2 图像预处理
然后结合数学形态学的分水岭算法对图像进行场景分割[9-10],分割出建筑主体目标的像素区域,使研究区域缩小到分割结果图像,提高目标立面拾取速度与精度;最后对建筑区域检测水平线,根据其消失点分类将建筑再分割成若干有序立面。预处理后的立面如图3 所示。

图3 对图2(b)的立面分割处理
2.2 稀疏特征点重建
预处理后的图像序列,用尺度不变特征转换(Scale Invariant Feature Transform,SIFT)方法[11]检测出稀疏的2D特征点,这些特征点落在颜色或轮廓变化剧烈的位置,如棱线、拐角等处。通过以下步骤恢复2D 特征点所对应的空间三维坐标,即3D 稀疏点:
Step1将序列I分成若干组连续视图,保证每组第一幅和最后一幅视图有一半以上的重叠场景,并对每组内的视图两两匹配2D 特征点,得到表征同一空间点的匹配点对。
Step2对组内每3 幅相邻图像Ii,Ii+1,Ii+2的匹配点建立对应,计算出这3 幅视图间表征同一空间点的对应点对。
Step3由基于绝对二次曲面的自标定位算法[12],利用对应点对,计算出Ii,Ii+1,Ii+2的摄像机参数Pi,Pi+1,Pi+2,及对应点对所表征的3D 稀疏点S(Ii,Ii+1,Ii+2)。
Step4添加视图Ii+3,Ii+4,对Ii+2,Ii+3,Ii+4重复Step2、Step3,计算3D 稀疏点S(Ii+2,Ii+3,Ii+4)。
Step5重复Step4,直到序列结束,得到输入序列的初始3D 稀疏点集S(I)。
为提高精度,本文使用随机抽样一致(Random Sample Consensus,RANSAC)方法对S(I)进行坐标预处理,去除S(I)中偏差较大的异常点和偏远点,使坐标更多地集中在建筑立面区域上。此时,得到的3D 稀疏点只能表示图像极少数像素点的空间位置,并不能覆盖全部场景。利用这些仅有的3D 稀疏点,分别计算场景地基线与矫正立面,从而恢复稠密点构成的3D 面结构。
2.3 地基线计算
得到稀疏点后,由以下步骤计算每幅视图场景地基线:
Step1计算每幅视图的一个垂下特征向量,即一个与地面垂直且指向下的三维方向向量。首先通过Hough 直线检测计算出立面上一条竖直方向的特征线,如建筑体的侧棱;然后搜索到若干位于或紧邻该特征线的3D 稀疏点(本文紧邻范围阈值为5 像素);再由这些点拟合空间直线并计算其单位方向d;对若干特征线同理操作后,按式(1)计算该视图最终的垂下特征向量n:

其中,M为特征线总数;
Step2将3D 稀疏点S={(xi,yi,zi)|i=1,2,…,N}沿垂下特征向量n=(a,b,c)向地平面做二维投影累计,N为稀疏点数。设S坐标系为O-XYZ,Z=(0,0,1)。构造式(2)旋转矩阵R:

由式(3)求S投影累计:
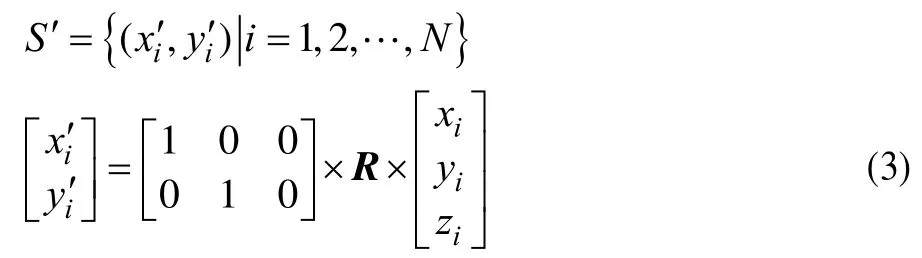
Step3对图I上由2.1 节分割的每个立面Fi,分别计算其所含3D 稀疏点得到的投影累计Si’后,由最小二乘法将Si’分段拟合为线段Bi,并顺序拼接所有的拟合线段,形成图I连续唯一的场景地基线B,B可直观地表示场景建筑外立面位置与地面布局。图4 为对图2 拟合的场景地基线B={B1,B2}。

图4 图2(b)的场景地基线
2.4 立面重建
仅用3D 稀疏点的度量信息,可快速矫正视图上投影失真的立面区域,得到具有真实纹理结构的矫正立面;然后,根据地基线的方位参数快速完成3D 模型的立面生长,即赋予矫正立面所有像点准确的空间3D 坐标,从而恢复该视图的建筑场景三维结构。
Step1设立面Fi上2D 特征点及其对应3D 稀疏点的点对
Step2记

当N取4 时,记式(4)为:

即有:

对全体点对根据式(6),可求得RANSAC 条件下最佳的点变换M。
Step3由式(7)将点变换M作用于Fi图像区域的所有像素点(xi,yi)(i=1,2,…,T;T为点总数),得到该立面的矫正点集Srected={(xi’,yi’)}。
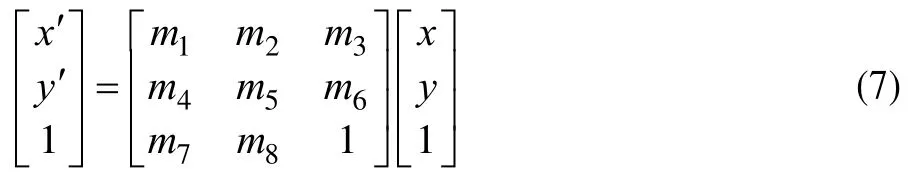
对Srected进行分段3 次Hermite 插值填充空隙,得到Fi更完整的矫正立面Fi’,如图5 所示。

图5 对图3(b)的矫正
Step4在Fi’上搜索垂下特征向量n所对应的2D 特征方向n’,并确定一个垂直于n’的扫描方向nscan;沿n’按nscan扫面Fi’的点,在Fi’的地基线上逐行建立该立面的3D 坐标(设坐标系为O-XYZ,则以地基线平面建立X、Y坐标,以顺序扫描的行值建立Z坐标),及映射像素点的纹理色;依次扫描该视图上所有立面,即能在同一地基线平面上建立该视图场景建筑的3D 模型。
在立面生长时,为保证相邻立面的准确对接,本文通过稀疏点校验,以稀疏点与地基线上其所对应的投影点为位置约束,剔除邻接立面的重复点。
2.5 场景模型融合
视图序列得到的若干立面模型,需要进行尺度调整和模型融合。由于稀疏点重建中每组连续视图得到的立面模型尺度相同,因此可先合并出每组视图对应的局部模型,再将局部模型融合成全部视图序列的一个建筑场景整体模型。该层次融合过程如图6 所示。
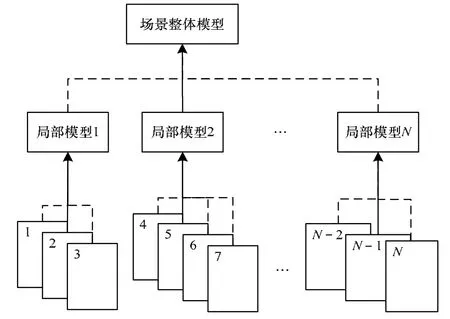
图6 场景模型层次融合
在每组连续视图中,选取位置居中的视图为基准图,根据其他邻接视图地基线与基准图地基线的二维拼接,依次将其他视图的模型归纳到基准图的场景模型之中,得到该组视图的一个局部模型;然后,以包含视图最多的局部模型为基准模型,归一化其他局部模型的尺度与基准模型一致;再根据局部模型间存在匹配对应的3D 点,检测各自地基线上的匹配对应部分,调整各局部模型的坐标系使其地基线拼合成唯一的场景地基线,据此完成局部模型合拢;最后,按式(8)对合拢模型上的重复点完成场景模型的融合:

其中,pi是N个局部模型中需要融合成唯一点p的点;disi是地基线平面上pi的投影点到基准模型地基线的距离。
3 实验结果与分析
本文在VS2010 下使用VC++、OpenCV 与GSL 科学计算库实现算法,为检验算法有效性与准确性,分别采用Merton College 的2 组室外建筑场景图像序列,应用本文算法进行三维立面重建。测量模型结果的立面角度和线比例,以定量评价建模精度。立面模型如图7、图8 所示,其图像尺寸分别为1 024×768 像素、900×768 像素,立面左起有序编号。

图7 Merton CollegeⅡ图像序列的立面模型

图8 Merton CollegeⅢ图像序列的立面模型
表1 所示模型中的立面夹角误差通过立面对应地基线(图4、图8(b))的夹角来测量,立面1、立面2、立面3 分别对应地基线段B1、B2、B3。图8 模型的平均角度误差比图7 模型大,主要由于图8 每个立面的像素点和稀疏点均较少,导致度量信息较少,地基线方位拟合精度较图7 低。

表1 模型立面的角度重建误差 (º)
图9 测量了图7 模型中分别包含203 269 个和124 528 个成像点的左、右2 个立面的夹角误差。横坐标表示使用数量/基准点数所占的比例。左、右立面的稀疏点基准点数分别取149 个和64 个,记录5 次实验的误差,每次实验将使用的稀疏点减少20%,其中使用比例为100%时的误差等于表1实验的0.3。
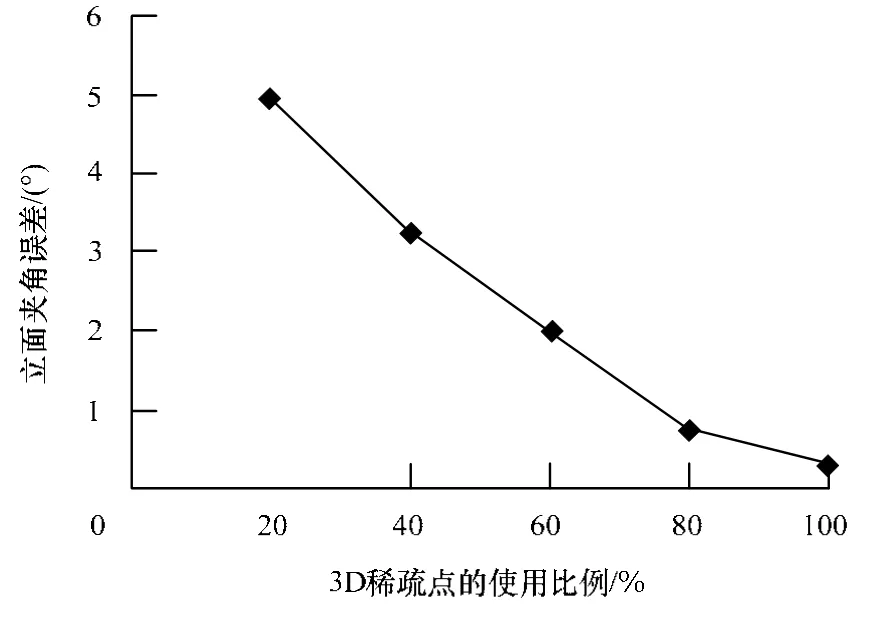
图9 图7 稀疏点使用比例与立面角度重建误差的关系
图9 表明,稀疏点的使用比例在20%(即左右立面各使用30 个和13 个稀疏点,占总成像点的0.13%)以上时,立面角度的重建误差在5°以内。立面夹角的误差随稀疏点使用比例增大而减少,且比例接近0 时趋近无穷大,这主要是由于立面方位信息建立在地基线上,3D 稀疏点数量越多,估算垂下特征向量越准确,计算拟合地基线的方位也越精确。
表2 测量了图8(c)模型立面上4 条线段的长度比例,取多次测量均值,其中,L1和L2、L3和L4分别位于同型的窗户。测量结果表明,本文算法对立面上线段长度比例的恢复误差在1%以内,该误差主要源自受成像尺寸影响的线段端点选择不准确,以及垂下特征向量拟合误差导致生长立面的扫面方向不严格平行于地基线。
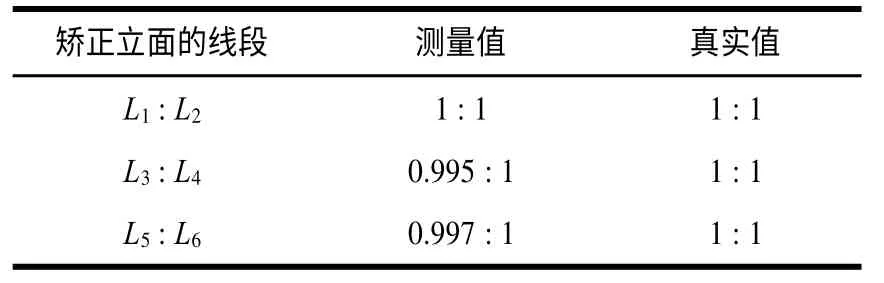
表2 图8(c)模型的线段长度比例重建误差
实验结果表明,地基投影算法能快速、高效地重建有正确角度、线比例结构的大尺度场景建筑立面模型,稀疏点占立面总像点0.13%以上时,地基投影法的立面角度重建误差小于5°,线比例误差在1%以内。在室外大场景建模工程的应用中,算法结果不仅能满足以规整立面为重建目标、对窗台等细部结构精度无严苛要求的实际需要,而且以该算法所得结果为基础模型,针对缺失结构扩展更加完整、精细的系统。
4 结束语
本文将场景地基线引入建筑场景的多视图立面建模,提出了地基投影算法,同时计算地基线与矫正立面,并利用地基线提供的立面空间方位信息,完成立面的三维生长与局部模型融合,从而便捷、有效地重建立面模型,避免了通常建模系统局限于稀疏重建与复杂设备的问题。实验结果证明,在一定的稀疏点使用比例范围内,本文算法能准确完成立面建模,所求的场景近似重建模型具有较高的立面角度和线比例重建精度,可满足工程需要。在此基础上,下一步工作将扩展补充缺失的纹理结构,精化场景模型,使之更适于高精度的大尺度场景建模。
[1]Wan Guowei,Noah S,Daniel C O,et al.Sorting Unorganized Photo Sets for Urban Reconstruction[J].Graphical Models,2012,74(1):14-28.
[2]刘培珺.基于图像序列的建筑物模型重建技术研究与实现[D].杭州:浙江大学,2003.
[3]Xiao Jianxiong,Fang Tian,Zhao Peng,et al.Image-based Facade Modeling[J].ACM Transactions on Graphics,2008,27(5):495-504.
[4]戴嘉境.基于多幅图像的三维重建理论及算法研究[D].上海:上海交通大学,2012.
[5]李 畅,刘亚文,胡 敏,等.面向街景立面三维重建的近景影像直线匹配方法研究[J].武汉大学学报:信息科学版,2010,35(12):1461-1465.
[6]代 勤,王延杰,韩广良.基于改进Hough 变换和透视变换的透视图像矫正[J].液晶与显示,2012,27(4):552-556.
[7]Pollefeys M.Detailed Real-time Urban 3D Reconstruction from Video[J].International Journal of Computer Vision,2008,78(2):143-167.
[8]王启帆,贾振红,覃锡忠,等.基于像素领域信息的自适应图像增强算法[J].计算机工程,2012,38(24):205-207.
[9]张桂梅,周明明,马 珂.基于彩色模型的重构标记分水岭分割算法[J].中国图象图形学报,2012,17(5):641-647.
[10]谢 闯,李磊民.基于彩色图像分割的路标检测算法研究[J].西南科技大学学报,2013,27(3):87-91.
[11]胡海青,谭建龙,朱亚涛,等.改进SIFT算法在文字图像匹配中的应用[J].计算机工程,2013,39(1):239-243.
[12]Pollefeys M,Gool L,Vergauwen M,et al.Visual Modeling with a Hand-held Camera[J].International Journal of Computer Vision,2004,59(3):207-232.
