基于小波与灰色方法的半球谐振陀螺寿命预测

代成龙，皮德常

(南京航空航天大学计算机科学与技术学院，南京 210016)

1 概述

由于半球谐振陀螺具有小体积、低噪声、高性能以及无磨损的特点，逐渐在国际上得到重视和应用[1-2]。但陀螺仪的成本高、批量小，给评估它们的可靠性以及预测其寿命带来了困难。同时，据相关统计数据显示[3]，惯导系统的故障40%由惯性平台产生，其中60%又来自陀螺仪。因此，研究陀螺仪的可靠性和寿命预测方法对惯导系统的可靠性评估具有重要意义。目前国内外关于半球谐振陀螺寿命预测方法的研究文献较少，一般只针对半球谐振陀螺的温度补偿[4]、动力学模型分析测试[5]以及随机漂移误差[6]等方面进行研究，但均未针对其寿命发表相关研究和报道。自文献[7]提出灰色系统理论后，该理论在处理部分未知参数的系统中得到了广泛应用。

灰色GM(1,1)模型是一种很适用的预测模型。累加生成操作[7]是其最重要的特点，该操作能有效降低数据的随机性。灰色理论的主要特点在于它不需要大量的数据进行预测，而只需要4个数据即可。因此，灰色预测方法在热导、电力消耗、集成电路、环境科学、农业等方面得到了广泛应用。为提高GM(1,1)的预测精度，一些研究人员对GM(1,1)进行了改进并应用到电力需求预测[8-9]。同时，在许多时间序列预测中，为了获取数据的规律，研究人员将小波分析方法也同样应用到预测当中[10-11]。

为克服半球谐振陀螺寿命预测方法不足的困难以及解决半球谐振陀螺寿命预测问题，本文结合以上研究，利用小波分析对半球谐振陀螺的漂移数据进行处理，对GM(1,1)模型进行残差修正，分析GM(1,1)模型与残差修正GM(1,1)模型在半球谐振陀螺寿命预测应用中的预测精度，通过灰色关联分析方法预测其工作寿命。

2 预测方法框架

半球谐振陀螺寿命预测方法结果框架如图1所示。首先选用适当的小波组合方法对漂移数据进行处理，然后对预处理后的数据建立GM(1,1)模型，接着利用残差值修正原始GM(1,1)并进行多周期数据预测，最后对GM(1,1)和残差修正GM(1,1)的预测精度进行分析，结合灰色关联方法分析出各半球谐振陀螺的失效阶段，最终获得半球谐振陀螺的预测寿命。

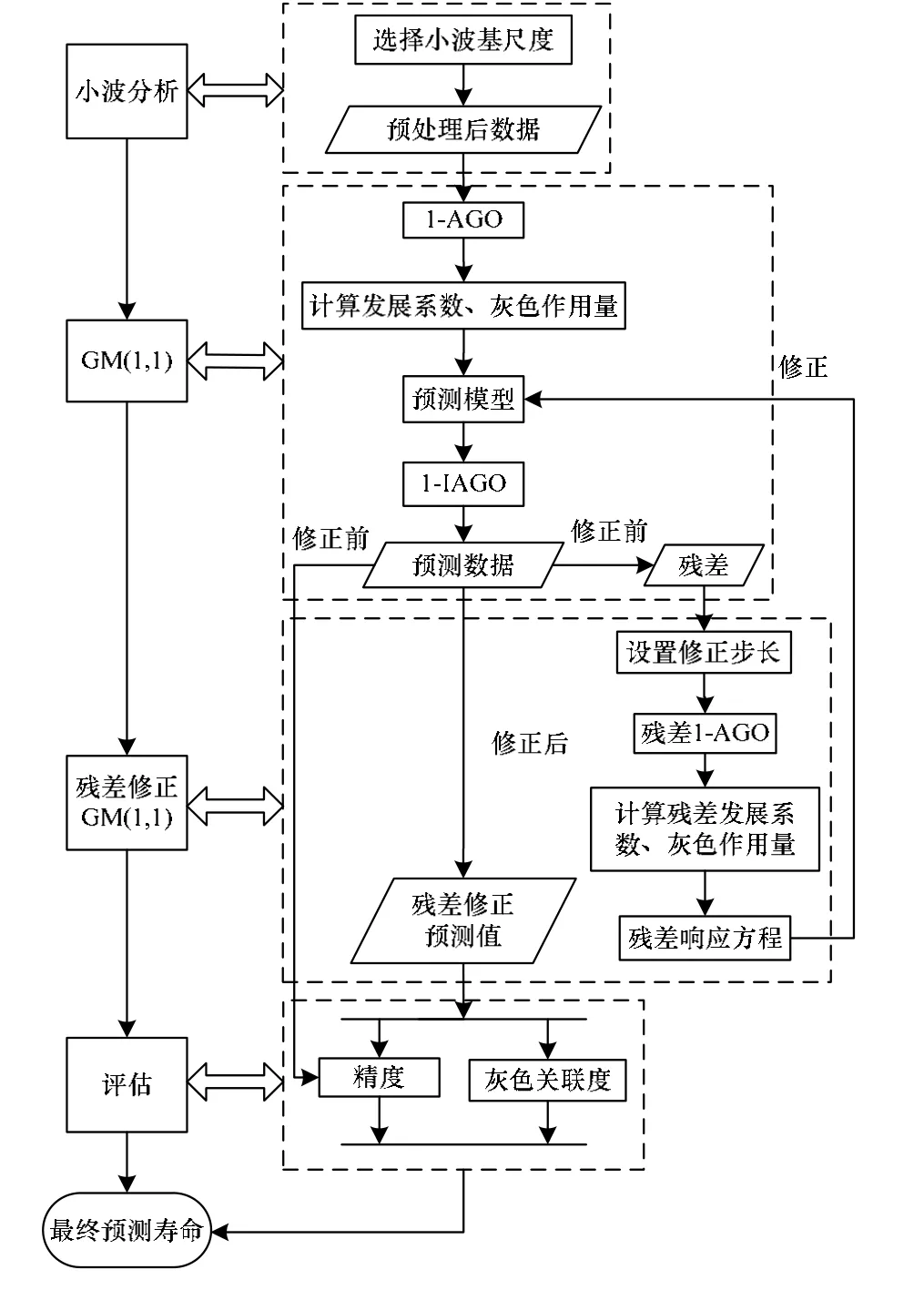
图1 预测方法框架

3 寿命预测模型

3.1 GM(1,1)模型

GM(1,1)模型具有时变特点：当获得新数据后，GM(1,1)模型将得到更新重建。

(1)假定原始序列为：

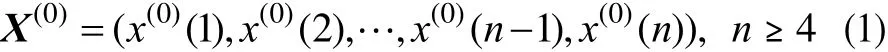
其中，X(0)为一非负数据序列；n为数据样本量。

(2)为减少随机性，对原始序列 X(0)作一次累加生成(1-AGO)，得到一组单调递增的新序列 X(1)：

其中：

(3)建立GM(1,1)模型为：

其中，T[a,b]为模型参数，且：

(4)根据式(4)、式(5)，x(1)(t)在k时刻的时间响应为：

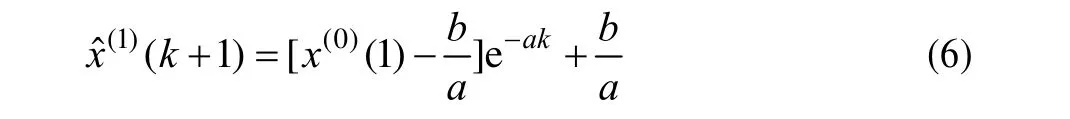
(5)使用1次累减生成(1-IAGO)，得到原始数据在k+1时刻的预测值：

3.2 残差修正GM(1,1)模型

残差修正GM(1,1)模型的目的在于对原始序列建立的GM(1,1)模型进行修正，以提高模型预测精度。其实质为对残差序列进行一次类似于GM(1,1)建模处理。

(1)可建模残差尾段(|ε(0)(k0)|,|ε(0)(k0+1)|,…,|ε(0)(n)|)记为：

(2)对可建模残差尾段进行1-AGO操作：

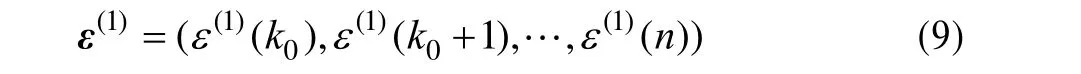
对其进行GM(1,1)建模，得到k时刻的时间响应式：

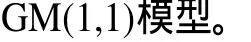
3.3 灰色关联分析模型

灰色关联分析是根据序列曲线几何形状的相似程度来判断它们之间的联系是否紧密。曲线越接近，相应序列之间的关联度就越大，反之越小。

设定 x0={x0(1),x0(2),…,x0(n}为参考序列，xi(i=1,2,…,m)为比较序列。其中：

故对于序列x0与xi中第k个数x0(k)与 xi(k)，其灰色关联度为：

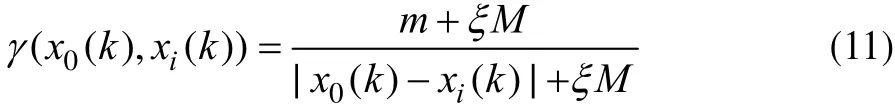
那么x0与xi2个序列之间的灰色关联度为：

γ(x0,xi)越大，说明xi对x0的关联程度越高，反之则越小。

4 实验与分析

4.1 数据

本文所用的HRG数据是由某科研单位提供，对4个型号不同的半球谐振陀螺的随机漂移(数据采集计算方法如式(13)和式(14)进行了测试，测试时间为2009-06-26至2012-02-08，共1590个数据。

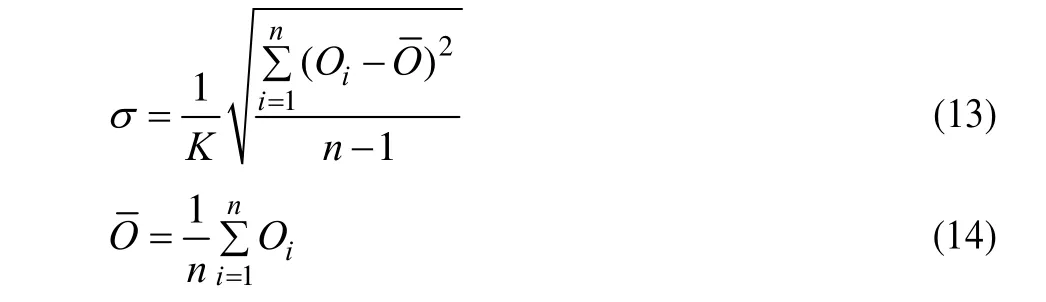
其中，Oi为经平均处理后得到的陀螺输出样本，单位为V；为陀螺输出平均值，单位为V；K为陀螺标度因数，单位为V/(°·s–1)；σ为随机漂移，单位为°/h。由4 个半球谐振陀螺随机漂移数据的计算方法可知，随机漂移值均为非负。

4.2 数据预处理

为降低原始漂移数据中的噪声，利用daubechies和symlets小波的不同组合对1#,2#,3#,4#HRG漂移数据进行分解、重构，找出处理结果相对较好的小波组合。

4个HRG的小波处理结果分别如图2所示，其中黑折线表示原始数据。

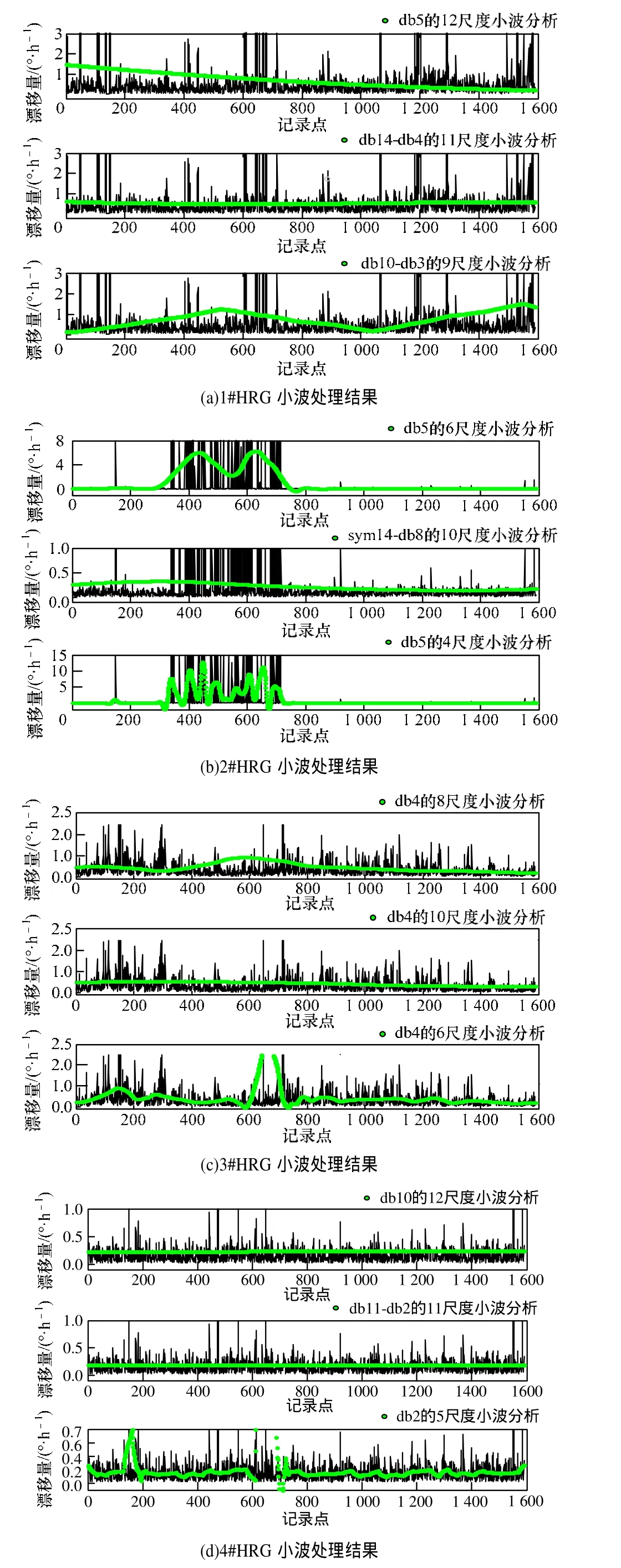
图2 4个半球谐振陀螺测试数据的小波预处理结果

图2(a)～图2(d)中第2子图的小波分析较其他子图能更好获取原始数据的规律，在后文的研究中，均采用第2子图中的小波预处理数据进行分析和预测。

4.3 模型预测与结果分析

国际上最长寿的10个航天器为：NASA外行星探测器Voyager2(1977.8–)，Voyager1(1977.9–)，NOAA 气象卫星GOES(1978.6–)， NASA 实验通讯卫星ATS-3(1967.11–2001)，海事卫星Mirasat F2(1976.6–2008.10)，NASA 遥感卫星Landsat 5(1984.3–2012.12)，NASA数据中继卫星TDRS-1(1983.4–2009)，NOAA 气象卫星GEOS 7(1987.2– 2012.4)，NASA数据中继卫星TDRS-3(1988.9–)以及NOAA气象卫星GOES2(1977.6–2001)。不难看出，以上最长寿的10个航天器目前为止的寿命约为24年～36年。因此，借鉴此10个最长寿航天器的寿命长度，本文对4个半球谐振陀螺的寿命预测长度设定为26年(即，9倍周期预测+1倍实验周期，约为26年)。分别采用GM(1,1)和经过残差修正后的GM(1,1)对以上4个HRG的预处理数据进行模拟序列预测及9倍周期数据预测(1周期为958天，每个周期共有1590个数据。9倍周期预测：从模拟序列预测之后预测出1590×9=14310个数据点)。4个半球谐振陀螺预测结果，即GM(1,1)与残差修正GM(1,1)模型的预测结果分别如图3～图6所示。9倍周期预测为各图横坐标[1-10]区域的预测结果。

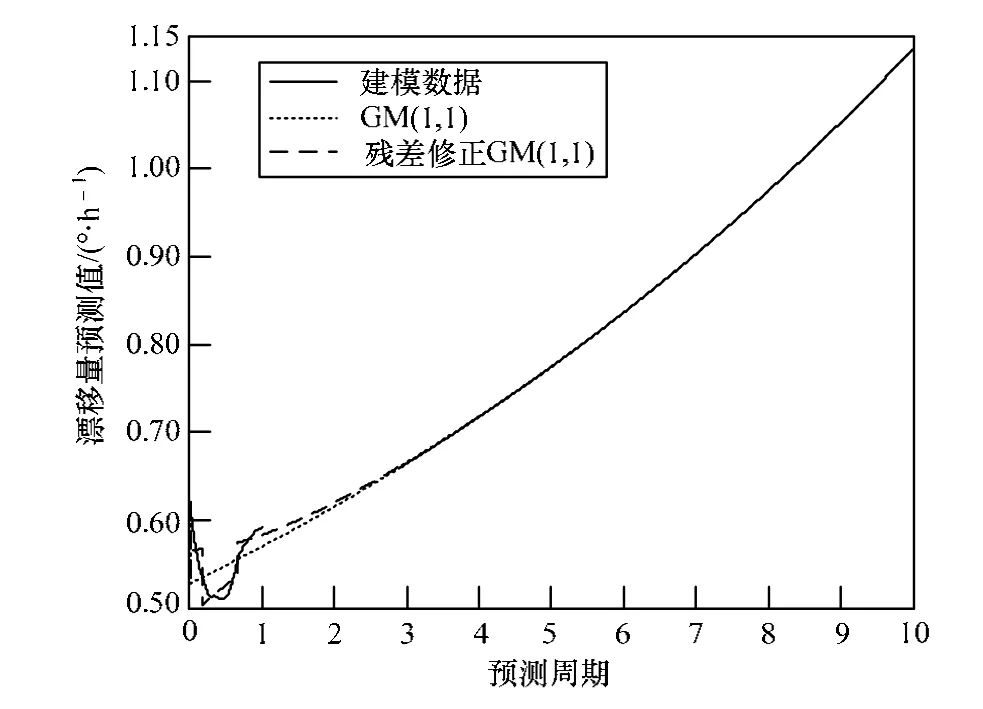
图3 1#HRG预测结果

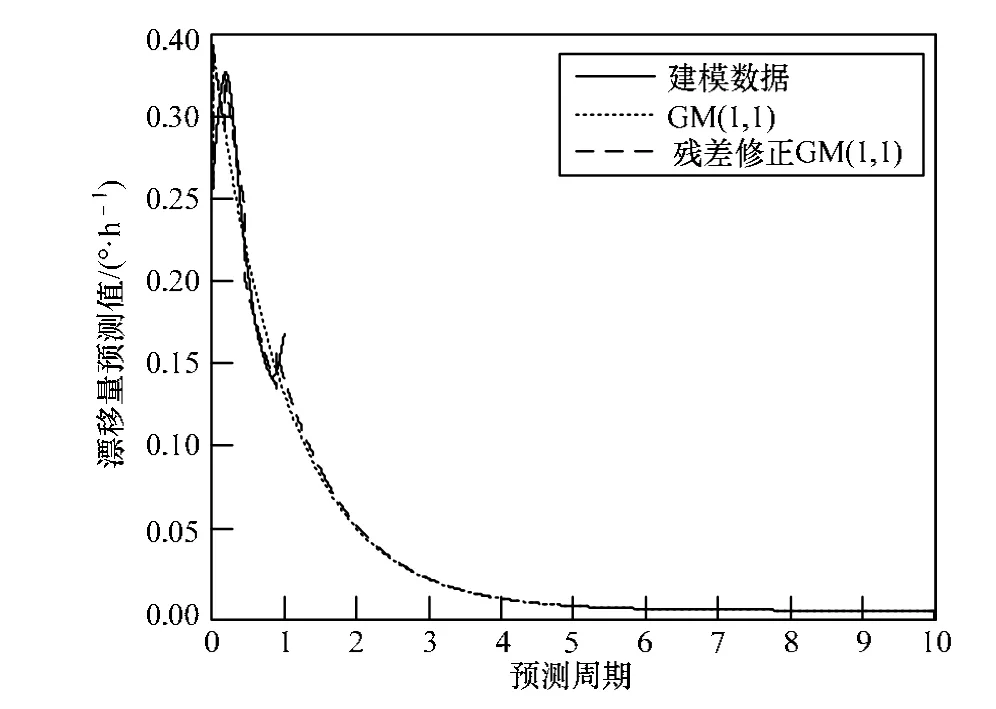
图4 2#HRG预测结果

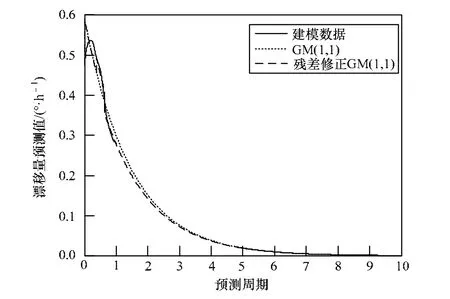
图5 3#HR结果

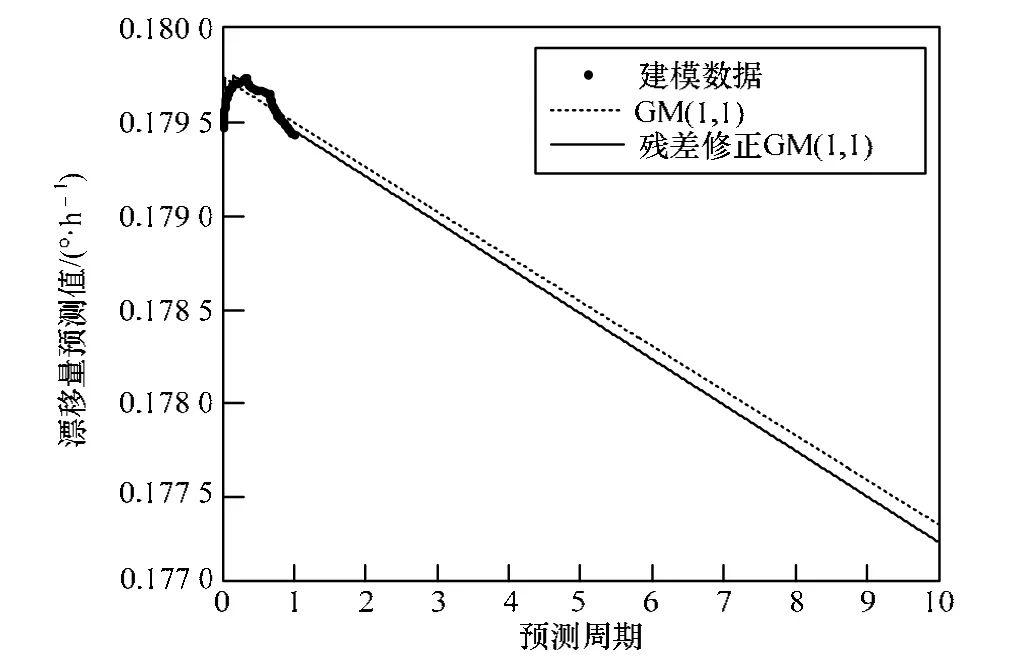
图6 4#HRG预测结果

根据图3～图6可知，4个半球谐振陀螺的GM(1,1)与残差修正GM(1,1)预测效果比较表明：残差修正GM(1,1)的预测效果优于GM(1,1)，修正后预测模型模拟序列(横坐标[0-1]区域)与建模序列更接近，关联更密切。由此推断，第1倍～第9倍周期预测，残差修正GM(1,1)的准确度高于GM(1,1)。

分别计算出GM(1,1)、残差修正GM(1,1)的模拟序列与建模序列之间的残差修正和、平均相对误差、均方根误差和标准均方误差，具体如表1所示。

表1 GM(1,1)与残差修正GM(1,1)的模拟序列预测精度

由表1所示，1#,2#,3#和4#残差修正GM(1,1)的平均相对误差、均方根误差、标准均方误差皆小于GM(1,1)，即利用残差修正GM(1,1)预测4个半球谐振陀螺的效果较GM(1,1)更好，具有更高的预测精度。

利用残差修正GM(1,1)模型对4个HRG分别进行1倍～9倍周期的漂移量预测，得到每个HRG的模型模拟序列、各周期预测序列与建模序列的灰色关联度，如表2所示。

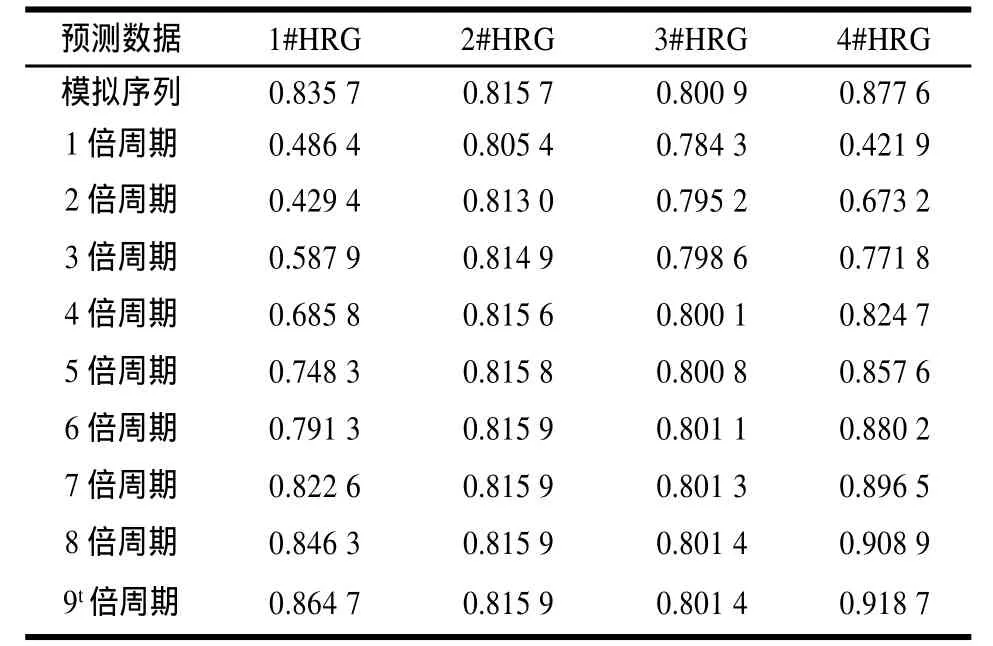
表2 10组预测数据与建模序列的灰色关联度

根据预测数据曲线，4个半球谐振陀螺的残差修正GM(1,1)模型的模拟序列曲线(各图横坐标[0-1]区域)与建模序列曲线最接近，相似度最高，第1倍～第9倍周期(横坐标[1-10]区域)预测数据曲线与建模序列曲线的相似度较小，根据3.3节中灰色关联分析方法，模拟序列的灰色关联度最高，第1倍～第9倍周期预测序列的灰色关联度较低，故以标准作为分析各半球谐振陀螺寿命的方法。

由表2可知，1#半球谐振陀螺的第8倍周期预测序列的灰色关联度为0.8463，首次超过模拟序列的灰色关联度0.8357，且此后各周期预测序列的灰色关联度均高于模拟序列的灰色关联度，因此，1#HRG的第8倍预测阶段作为该类型陀螺仪的失效阶段。则1#陀螺仪预测寿命为9倍周期(即，8倍预测周期+1个实验周期=9倍周期，1周期为958天)，即958×9=8622天，约23.62年；同理，2#半球谐振陀螺的预测寿命为958×6=5748天，约15.74年；3#HRG预测寿命为958×7=6706天，约18.37年；4#HRG预测寿命为958×7=6706天，约18.37年。参照国际上最长寿命的10个航天器寿命，本文预测出的4个半球谐振陀螺的寿命符合实际情况，验证了本文采用的复合方法的正确性。

5 结束语

本文针对国内外半球谐振陀螺寿命预测方法研究较少的情况，提出了一种基于小波分析与灰色关联的灰色系统长寿命预测方法。该方法利用daubechies和symlets小波分解、重构半球谐振陀螺的漂移数据，获得规律性更强的低噪声建模数据，然后对GM(1,1)进行残差修正，使用该修正后的模型进行多周期预测，预测结果表明残差修正GM(1,1)的预测模拟数据精度高于GM(1,1)。最后利用灰色关联方法分析、判断出各半球谐振陀螺的失效阶段，从而预测各陀螺仪的寿命：1#,2#,3#和4#这4个半球谐振陀螺一般可正常工作15年以上。根据国际上航天器的工作寿命情况，利用文中的复合方法得到的半球谐振陀螺寿命值具有一定的可信度，因而该预测方法和预测结果可为研究半球谐振陀螺工作寿命的机构提供相应参考。虽然文中的复合方法较传统的GM(1,1)能更好地处理噪声数据，得到更高精度的模拟序列并进行长周期寿命预测，但在实验过程中，该方法自我学习能力不强，对数据规律要求较高，故今后会继续研究学习能力更好的方法，对它们进行优化改进，从而更好地适应长期寿命预测场合，并将改进的方法应用到半球谐振陀螺工作寿命预测当中。

[1]Rozelle D M.The Hemispherical Resonator Gyro:From Wineglass to the Planets[C]//Proc.of the 19th AAS/AIAA Space Flight Mechanics Meeting.Savannah,USA:AAS/AIAA Press,2009:1157-1178.

[2]吕志清.半球谐振陀螺(HRG)信号处理技术[J].中国惯性技术学报,2000,20(4):58-61.

[3]冯培德,张保京,富 铁.可靠性工程技术在航空惯性导航系统研制中的应用[J].中国惯性技术学报,1996,4(4):56-65.

[4]Li Boran,Wu Yiran,Wang Changhong.The Identification and Compensation of Temperature Model for Hemispherical Resonator Gyro Signal[C]//Proc.of the 3rd International Symposium on Systems and Control in Aeronautics and Astronautics.Harbin,China:[s.n.],2010:398-401.

[5]Yang Qian,Yi Guoxing,Wang Henian,et al.Kinetic Model Analysis and Testing of HRG[C]//Proc.of the 1st International Symposium on Systems and Control in Aerospace and Astronautics.Harbin,China:[s.n.],2006:105-109.

[6]Peng Hui,Fang Zhen,Lin Ke,et al.Error Analysis of Hemispherical Resonator Gyro Drift Data[C]//Proc.of the 2nd International Symposium on Systems and Control in Aerospace and Astronautics.Shenzhen,China:[s.n.],2008:1-4.

[7]邓聚龙.灰色论基础[M].武汉:华中科技大学出版社,2002.

[8]Hsu C C,Chen C Y.Applications of Improved Grey Prediction Model for Power Demand Forecasting[J].Energy Conversion and Management,2003,44(14):2241-2249.

[9]Albert W L,Chi S C,Chen J H.An Improved Grey-based Approach for Electricity Demand Forecasting[J].Electric Power Systems Research,2003,67(3):217-224.

[10]Soltani S.On the Use of the Wavelet Decomposition for Time Series Prediction[J].Neurocomputing,2002,48(1/4):267-277.

[11]Mabrouk A B,Abdallah N B,Dhifaoui Z.Wavelet Decomposition and Autoregressive Model for Time Series Prediction[J].Applied Mathematics and Computation,2008,199(1):334-340.