改进多样性和局部优化能力的引力搜索算法

王 蕾，潘 丰

(江南大学轻工过程先进控制教育部重点实验室，江苏 无锡 214122)

1 概述

由文献［1］提出的引力搜索算法(Gravitational Search Algorithm，GSA)是一种启发式算法，是适合于大范围搜索空间问题的全局搜索算法。研究证明，GSA 的全局搜索能力明显优于粒子群优化算法［2］、遗传算法［3］、蚁群算法［4］、中心引力算法［5］等智能优化算法。目前，GSA 已成功地应用于无人机航路规划问题［6］、多目标最优能流问题［7］、电厂锅炉废气排放模型［8］、原型分类［9］等。

在算法改进方面，文献［10］对GSA 引入反馈策略，均衡优化了算法全局与局部搜索能力，文献［11］在GSA 中引入了三角范数算子，进一步提高了算法的全局搜索能力。文献［12］对GSA 的记忆性进行改进，提出记忆改进GSA (Memory Gravitational Search Algorithm，MGSA)，在一定程度上改善了GSA的局部搜索能力。

研究发现，以往的算法改进主要针对GSA 算法的全局与局部搜索能力，但GSA 在搜索过程中，每个粒子都向质量大的粒子靠近，在这种方式下，由于多样性的失去，粒子群易在全局近优点的吸引下陷入局部最优，发生早熟收敛。在引力搜索算法中添加局部优化策略和保持多样性策略，从而在保留强大全局搜索能力与加强局部搜索能力的同时，更可以保持种群多样性，避免早熟现象的发生。

本文提出了在引力搜索算法中添加多样性和局部优化策略的方法。主要在粒子进化公式中引入粒子群算法［2，13］中的局部最优解思想;在多样性丢失时，采用细菌趋化中排斥操作［14-15］的概念，改进粒子群整个搜索过程中的局部搜索能力，提高算法在迭代后期的种群多样性，最后通过测试基准函数验证改进算法的有效性，并分析测试结果。

2 标准引力搜索算法

引力搜索算法是近年来提出的用于解决优化问题的启发式算法，和其他现有的著名启发式优化算法相比，引力搜索算法具有更好的全局搜索能力和更快的收敛能力［1，13］。算法中每个粒子有4 个特征:即位置、施力质量、受力质量和惯性质量。每个粒子的位置就对应了一个优化问题的解，随着一次次的迭代，粒子都被质量大的粒子(代表问题的最优解)所吸引，直到停止条件满足，则停止迭代［1，10，13］。

引力搜索算法中粒子的初始位置是随机生成的。假设一个由N 个粒子组成的粒子群在D 维的搜索空间以一定的速度飞行，定义第i 个粒子的位置为:

根据牛顿万有引力定律，在第d 维空间上第j 个粒子对第i 个粒子的作用力可以定义为:

其中，Mi(t)和Mj(t)分别是粒子i 与粒子j 的惯性质量;G(t)是在t 时刻的引力系数;Rij(t)是t 时刻粒子i与粒子j 之间的欧式距离:Rij(t)=‖Xi(t)，Xj(t)‖2;ε 代表很小的常数。根据式(3)和式(4)利用适应值更新粒子i 的惯性质量Mi(t):

其中，fiti(t)是指粒子i 在时刻t 的适应值;best(t)和worst(t)分别是指在时刻t 整个粒子群的最优适应值和最差适应值;而mi(t)为计算粒子质量的中间变量。粒子的惯性质量Mi(t)越大则说明粒子对其他粒子有更大吸引力，随着迭代的进行，其他粒子纷纷向其靠拢。反之其自身受其他粒子的吸引力对本身影响就很小，导致其移动速度也变慢。所以，粒子惯性质量越大则移动速度越缓慢，位置改变越小，而其他粒子向其位置聚拢。因此，粒子惯性质量越大意味着其本身位置越接近最优解。在求解目标函数最小值问题时，best(t)和worst(t)定义如下:

在求解目标函数最大值问题时，best(t)和worst(t)定义如下:

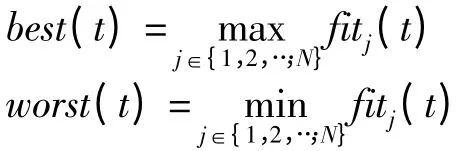
值得指出的是，引力系数G(t)决定了GSA 算法的性能，搜索开始时就应对引力系数G(t)初始化，G(t)值随着时间逐步减小，从而控制搜索精度。G(t)是关于初始值G0和迭代次数β 的函数，定义为:

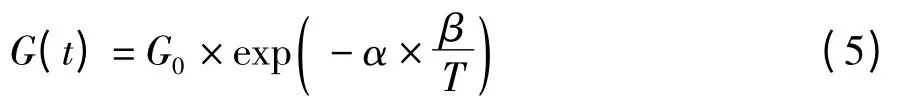
其中，G0是引力系数初始值;α 是个常数;β 是当前迭代次数;T 是最大迭代次数。

其中，kbest 是一个随着时间增加而减少的线性函数。一开始的值为搜索空间中粒子总数，表示所有粒子相互间都有作用力，这样就增加了粒子的全局搜索能力，避免陷入局部最优;随着迭代过程的进行，应逐步增加粒子的局部搜索能力，故kbest 值线性减少，最终值应为1，此时只有一个惯性质量最大的粒子i 作用于其他粒子。依据粒子所受作用力公式，若粒子惯性质量为Mi(t)，那么粒子i 的加速度为:

基于万有引力定律的搜索策略，粒子i 在下一时刻的速度和位置的进化公式为:

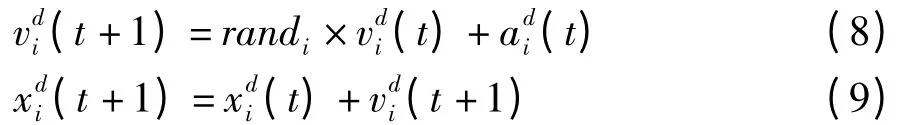
其中，randi是介于［0，1］随机产生的数。

3 引力搜索算法的改进

3.1 多样性和局部优化策略及其实现

基于群体的启发式算法有2 个共同点:探索与开发［1］。GSA 算法中惯性质量大的粒子产生更广的吸引范围和更大的吸引力，更易吸引其他粒子，使其他粒子向其靠近，即向最优解靠拢［1，13］。而根据式(2)、式(6)、式(7)可知，当粒子i 接近最优解时，由于所受引力加大，速度将不断加快，粒子易在最优位置的附近来回振荡，导致粒子搜索精度不高，种群多样性丢失。而根据式(8)、式(9)可知，引力搜索算法在迭代过程中粒子i 的下一刻位置仅取决于下一刻的速度信息和当前的位置信息，无法捕捉到最优位置信息帮助粒子本身寻优至最优位置。针对以上问题，引入PSO 算法［14，16］中群体历史最优位置及自身历史最优位置的概念，同时加入细菌趋化中的排斥操作［15］，改进引力搜索算法中粒子的局部搜索优化能力与提高种群多样性。其中，多样性的度量公式如下:

根据迭代过程中粒子群不同的多样性选择不同的速度更新方式。当diversity(N)≥dmax时，粒子就向当前最优位置和自身历史最优位置靠近，转向吸引操作，以增加局部寻优能力。运用式(11)、式(12)进行速度更新和位置更新:

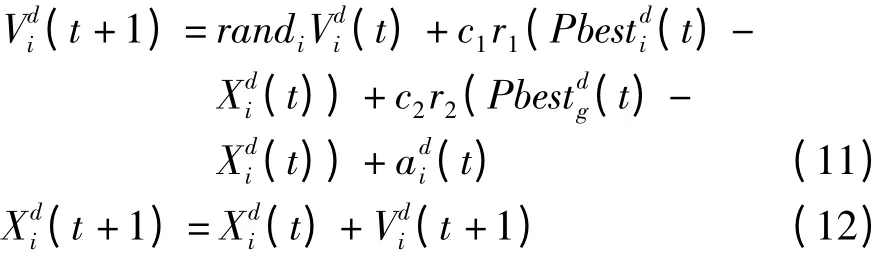
当diversity(N)≤dmin时，粒子就逃离当前最差位置和自身历史最差位置，转入排斥操作，以增加种群多样性，使粒子搜索空间其他位置，有助于粒子发现更好的位置。运用式(13)、式(14)进行速度更新和位置更新:

其中，randi，r1，r2，R1，R2是介于(0，1)产生的随机数;c1，c2，C1，C2为学习因子，c1，C1调节粒子飞向自身最优位置的步长，c2，C2调节粒子飞向全局最优位置的步长分别表示在时刻t 粒子i 的历史最优、最差位置分别表示在时刻t 种群的历史最优、最差位置［13-14］。

3.2 改进算法的分析

对于上述提出的改进的引力搜索算法可引入微分方程对其进行描述，采用控制理论对其搜索能力进行分析［17］。在速度更新公式式(11)、式(13)中，采用关于和的某个函数f 来代替(t)，函数f 为线性函数组合，表示为:

其中，τ 为区间(0，1)间随机选取的常数。现将式(15)分别代入式(11)、式(13)可得:

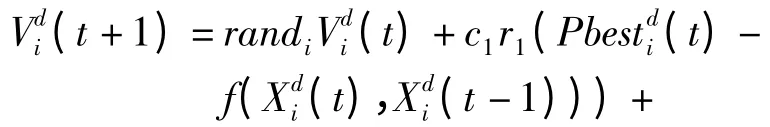
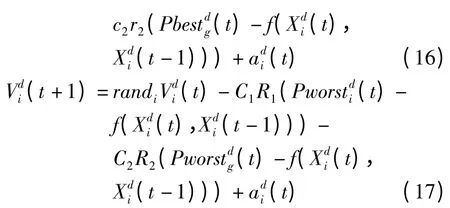
以式(16)为例进行分析，分解可以得到:

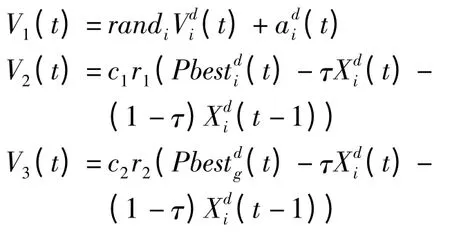
其中，V2，V3是研究算法收敛至局部最优位置和全局最优位置的部分。设γ1=c1r1，γ1为常数。

(1)对于V2，更新方程为:

由此可得:

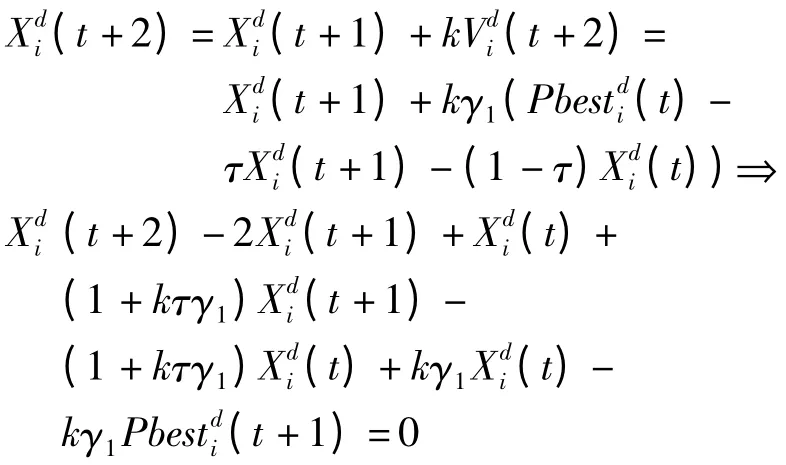
利用微分方程［17］:为单位阶跃函数，可得到［18］:

根据控制理论得到系统传递函数，利用拉普拉斯反变换可得［19］:

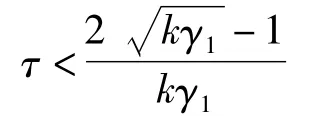
又因为τ∈(0，1)，则:

(2)分析V3时同理，参数选择满足就可获得振荡环节。

而对于式(17)，算法分析如式(16)。只要参数选择满足条件，系统就可以获得振荡环节。与采用一阶微分方程描述的惯性环节相比，采用二阶微分方程描述的振荡环节能够使粒子在全局最优位置和局部最优位置附近进行幅度由大到小的搜索，大大提高粒子速度的利用率和算法的全局与局部搜索能力。

改进算法的流程如图1 所示。

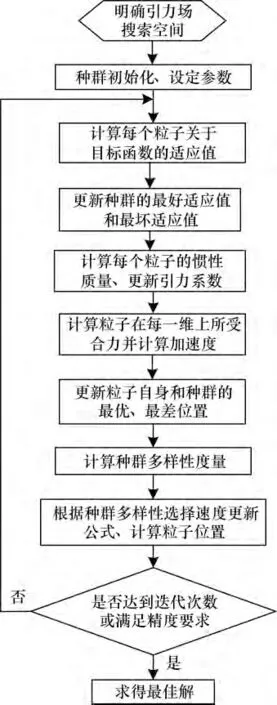
图1 引力搜索算法流程

4 实验与结果分析

为验证本文算法的有效性，选用以下4 个测试函数进行测试，如表1 所示。

表1 测试函数

为更好地验证多样性与局部优化能力改进的GSA (Diversity and Local Optimization GSA，DLOGSA)算法的优越性，同时采用标准GSA(Standard GSA，SGSA)和MGSA 对上述4 个函数进行寻优。采用Windows XP 为实验仿真平台，Matlab2010b 版本进行仿真模拟。粒子种群数目设为50，每个算法独立运行20 次，最大迭代次数设置为1 000，表1 中n 取30。按引力系数式(5)，G0设定为100，β 设定为20，按速度更新式(11)、式(13)，取学习因子c1=c2=C1=C2=0.5。其中多样性阈值dmax=2.5 ×10-3，dmin=5.0 ×10-5。运行完毕后统计运行结果的平均值、中值和标准方差。

对于每个测试函数，每种算法分别独立运行20 次，表2 给出了20 次实验后3 种算法对每个测试函数的优化结果的平均值、中间值和标准方差。

表2 标准测试函数优化结果比较

Sphere 是简单的单峰值函数，只有一个全局最优解，SGSA、MGSA 和DLOGSA 在搜索过程中都可快速收敛至最优值，不会陷入局部最优。如图2 所示，3 种算法的过程曲线较为相似，在迭代过程中始终保持着较快的收敛速度。但DLOGSA 算法优化结果从迭代开始就明显优于SGSA 和MGSA，迭代快结束时DLOGSA 算法收敛速度加快，获得了良好的收敛效果。

图2 Sphere 函数优化过程曲线

Noise 函数是含有高斯噪声的4 次函数，不考虑噪声影响时，函数具有全局最小值f(0，0，…，0)=0。从图3 可以看出，在这个测试函数中，MGSA 在前100 次迭代中优化结果明显大于 SGSA 和DLOGSA，在100 次～200 次迭代过程中3 种函数都快速收敛，很快收敛到最优值，但在测试函数200 次迭代过程以后SGSA 和MGSA 就陷入早熟收敛。相比较而言，DLOGSA 在200 次迭代以后仍进化振荡向下，进一步收敛，最终找到最优结果，其优化结果明显优于SGSA 和MGSA。

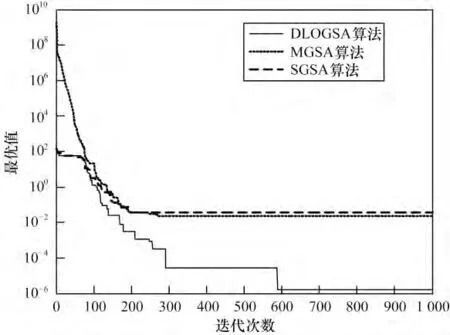
图3 Noise 函数优化过程曲线

Rastrigin 函数是一个多峰值函数，本次仿真模拟中选取30 个维数，故该测试函数是多峰高维函数。如图4 所示，在整个优化的过程中，DLOGSA 在迭代过程中一直保持很快的收敛速度，DLOGSA 算法的优化结果也明显优于SGSA 和MGSA。SGSA和MGSA 收敛过程类似，在迭代200 次左右就陷入局部最优，表现为进化曲线平直，而DLOGSA 持续进化振荡向下。该结果表明对于这类复杂函数，DLOGSA 算法具有优越性，这在于在进化过程中不仅有吸引操作更有排斥操作在起作用，很好地保持了种群的多样性，避免函数陷入早熟收敛。

图4 Rastrigin 函数优化过程曲线

Griewank 函数是典型的多模态函数，具有大量局部极值，可以很好地检验算法的全局搜索性能。如图5 所示，对于SGSA 算法的改进并未影响SGSA原有的良好全局搜索性能。迭代之初，3 种算法性能接近，在迭代100 次～200 次之间，DLOGSA 的收敛速度就明显快于 SGSA 和 MGSA，而在迭代200 次～300次之间，SGSA 已收敛到局部最优值，DLOGSA 和MGSA 仍持续振荡向下，进一步收敛，最终DLOGSA 优化结果仍优于MGSA。

图5 Griewank 函数优化过程曲线

5 结束语

本文在引力搜索算法的基础上，提出一种改进对种群多样性和粒子局部搜索能力的方法。针对引力搜索算法中粒子局部搜索能力弱和种群易陷入早熟收敛的情况，引入粒子群算法中的局部搜索思想和细菌趋化理论，使得粒子在进行速度更新时，对历史最优位置和自身最优位置都具有记忆性，加强局部搜索能力;引入的多样性策略决定搜索粒子是实行吸引操作还是排斥操作，从而实现全局搜索与局部搜索的平衡，最大程度地保持种群多样性。用4 个典型的标准函数进行测试，验证了改进后的算法搜索能力有较大的提高。而针对不同的应用场合选择合适的多样性阈值是今后的工作重点。

［1］Rashedi E，Nezamabadi-pour H，Saryazdi S.GSA:A Gravitational Search Algorithm ［J］.Information Sciences，2009，179(13):2232-2248.

［2］Trelea I C.The Particle Swarm Optimization Algorithm:Convergence Analysis and Parameter Selection［J］.Information Processing Letters，2003，85(6):317-325.

［3］马永杰，云文霞.遗传算法研究进展［J］.计算机应用研究，2012，29(4):1201-1206，1210.

［4］高 尚，江新姿，汤可宗.蚁群算法与遗传算法的混合算 法［C］//第26 届中国控制会议论文集.北京:北京航空航天大学，2007:701-704.

［5］Formato R A.Central Force Optimization:A New Metaheuristic with Applications in Applied Electromagnetic［J］.Ballooning，2007，77:425-491.

［6］李 沛，段海滨.基于改进万有引力搜索算法的无人机航路规划［J］.中国科学，2012，42(10):1130-1136.

［7］Bhattacharya A.Solution of Multi-objective Optimal Power Flow Using Gravitational Search Algorithm［J］.IET Gener Transm Distrib，2012，6(8):751-763.

［8］牛培峰，肖兴军，李国强.万有引力搜索算法在电厂锅炉NOx排放模型中的应用研究［J］.自动化博览，2011，(S2):87-92.

［9］Abbas B，Nezamabadi-pour H.A Prototype Classifier Based on Gravitational Search Algorithm［J］.Applied Soft Computing，2012，12(2):819-825.

［10］顾斌杰，潘 丰.基于反馈策略的引力搜索算法及其在支持向量机中应用［J］.计算机应用，2013，33(3):806-809.

［11］徐 遥，安亚静，王士同.基于三角范数的引力搜索算法分析［J］.计算机科学，2011，38(11):225-230.

［12］李春龙，戴 娟，潘 丰.引力搜索算法中粒子记忆性改进的研究［J］.计算机应用，2012，32 (10):2732-2735.

［13］徐 遥，王士同.引力搜索算法的改进［J］.计算机工程与应用，2011，47(35):188-192.

［14］Niu B，Zhu Y L，He X X，et al.An Improved Particle Swarm Optimization Based on Bacterial Chemotaxis［C］//Proceedings of the 6th World Congress on Intelligent Control and Automation.Shenyang，China:［s.n.］，2006:3193-3197.

［15］Soujik V，Wingreen N S.Responding toChemical Gradients Bacterial Chemotaxis［J］.Current Opinion in Cell Biology，2012，24(2):262-268.

［16］Liang J J，Qin A K，Suganthan P N，et al.Comprehensive Learning Particle Swarm Optimize for Global Optimization of Multimodal Functions［J］.IEEE Transactions on Evolutionary Computation，2006，10(3):281-295.

［17］同济大学数学系.高等数学［M］.北京:高等教育出版，2007.

［18］崔志华，曾建潮.基于控制理论的微粒群算法分析与改进［J］.小型微型计算机系统，2006，27(5):849-853.

［19］胡寿松.自动控制原理［M］.北京:科学出版社，2008:89-99.