厚度对变截面钢板弹簧应力分布的影响
2014-12-02唐俊琦朱晨虹
唐俊琦 朱晨虹
(武汉理工大学现代汽车零部件技术湖北省重点实验室 武汉 430070)
0 引 言
相比传统的钢板弹簧,变截面钢板弹簧片数少、质量轻、疲劳寿命长,而且它对整车的轻量化和提高整车舒适性和平顺性有着十分重要的意义.变截面钢板弹簧是根据等应力梁的原理制造的,即是变截面钢板弹簧应力分布要较为均匀.但改变几何尺寸会改变应力分布,钢板弹簧受车型的限制,长度和宽度不宜改变,因此研究厚度对变截面钢板弹簧应力分布的影响是有意义的.
对于变截面钢板弹簧,已经进行了很多的研究.文献[1]探讨了变截面钢板弹簧的结构形式,推导了刚度和质量的设计公式.文献[2-6]应用有限元的分析方法分析了少片变截面钢板弹簧的力学特性.文献[7]根据比例尺效应,讨论了变截面钢板弹簧最大应力点的选择问题.文献[8]利用弹性多体动力学模型分析变截面钢板弹簧迟滞特性与动应力.文献[9]用等效一维系统分析变截面钢板弹簧.其中,还没有通过改变变截面钢板弹簧的厚度来研究变截面钢板弹簧的应力分布的研究.
利用用有限元分析方法来揭示厚度对钢板弹簧加载后应力分布的影响.通过建立多个不同厚度的钢板弹簧模型计算,得到不同厚度下钢板弹簧的应力分布,对比分析厚度的变化对钢板弹簧应力的影响.
1 有限元模型
1.1 模型描述
变截面钢板弹簧是梯形结构且为对称体,所以取钢板弹簧的1/2进行建模.这里利用有限元分析软件ABAQUS建立参数化模型,以便快速建立不同厚度的钢板弹簧模型.变截面钢板弹簧模型建模较为简单,建模的关键在钢板弹簧的下表面.每片钢板弹簧有一定的曲率,由于横截面的变化,钢板弹簧的下表面就成为了一个特殊的曲面.解决的方法是在变截面区的下表面在纵向选择几个特征点,再用样条曲线来拟合,见图1.
图1 变截面钢板弹簧1/2模型
钢板弹簧受力弯曲属于大变形过程且不会达到塑性变形,所以应该是非线性弹性力学分析.使用8节点减缩积分(C3D8R)单元为钢板弹簧划分网格,其中的减缩积分和沙漏控制可以提高计算效率.钢板弹簧材料使用60Si2Mn,板簧长度为660mm,曲率半径为2000mm,弹性模量和泊松比分别为206GPa和0.3.
1.2 约束条件及载荷
在钢板弹簧模型的下表面中央平直段施加固定约束,对其上表面不施加约束,任其自由变形.同时在钢板弹簧端部施加垂直向下的线载荷模拟钢板弹簧加载过程.对于不同厚度的钢板弹簧施加相同载荷,这样使钢板弹簧的应力分布具有可比性.
2 结果与分析
2.1 计算条件
钢板弹簧厚度比γ为钢板弹簧的端部厚度(h1)与根部厚度(h2)之比.用有不同厚度比和根部厚度的钢板弹簧其应力分布也不相同.这里为分析厚度与厚度比对应力分布的影响,分为5种不同的厚度比和五种不同的根部厚度来计算.
条件1:γ=0.3;h2=12,13,14,15,16 mm;h1=3.6,3.9,4.2,4.5,4.8mm.
条件2:γ=0.4;h2=12,13,14,15,16 mm;h1=4.8,5.2,5.6,6,6.4mm.
条件3:γ=0.5;h2=12,13,14,15,16 mm;h1=6,6.5,7,7.5,8mm.
条件4:γ=0.6;h2=12,13,14,15,16 mm;h1=7.2,7.8,8.4,9,9.6mm.
2.2 变截面钢板弹簧受载时的应力分布
钢板弹簧的应力分布见图2,图中钢板弹簧在长度方向明显的分层,其中大应力区域在变截面区的后部.在厚度方向钢板弹簧的应力也是分层的,中间层的应力值要小于上下两层.根据应力公式:

式中:σ为横截面任意一点应力;M为横截面上的弯矩;Iz为很截面对中性轴的惯性矩;y为横截面上点对中性轴距离.可以看出y越大,σ越大,即距离中性轴越远的点应力越大.
由图1可见,板簧中间夹紧段在厚度与长度方向变化不均匀,这是由于在板簧受力弯曲时在夹紧处一小段区域仍有力传入所致.
2.3 根部厚度对变截面钢板弹簧应力分布的影响

图2 变截面钢板弹簧应力云图
当以γ=0.5(条件3)时为例,观察不同的根部厚度对钢板弹簧应力分布的影响.对每片钢板弹簧的中心对称截面上,沿钢板弹簧长度方向选取所有节点,得到最大应力在钢板弹簧长度方向的分布曲线,见图3.可以看出不同厚度下钢板弹簧的应力分布十分类似,而且应力分布较为复杂且是高度非线性的.应力首先显著地增长,之后增长缓慢,也就是说这一段的应力分布比较平缓.在变截面区后部应力再次快速增长达到峰值后开始下降.在骑马螺栓要夹紧的中间段时应力快速的下降,在根部附近应力下降趋于平缓直至应力最小点.总体上看,这一半的钢板弹簧模型的应力分布近似为“n”形,即端部和根部的应力值小,中间变截面区应力值大.

图3 变截面钢板弹簧应力分布曲线
根据不同厚度的钢板弹簧应力分布的对比可以看出,随着钢板弹簧的厚度增加,对应位置的应力值逐渐减小,而且在长度方向的应力分布更加的趋向一致.也就是说厚度越厚,应力分布越均匀,等应力梁的效果越好.导致这样结果的原因是:在相同厚度比情况下,随着厚度的增加,根部厚度和端部厚度之差在增大,而且长度方向上应力是逐渐增大的,大应力区在钢板弹簧变截面的后部.对于厚度越大的钢板弹簧,其根部厚度与端部厚度的差值就越大,由材料力学可知厚度大应力变小,这样钢板弹簧在长度方向的应力值差别变小,钢板弹簧应力分布均匀.
图4是在中心截面分别选取距离端部分别为d=0.11,0.22,0.33,0.44,0.55m 处钢板弹簧上表面的节点,取最大应力做厚度-应力曲线图.发现在0.11,0.22,0.33 m 处,随着根部厚度增加应力下降较为平缓,在0.44与0.55m 处曲线下降较快,这说明随着厚度增加,靠近根部的变截面区应力下降更显著.
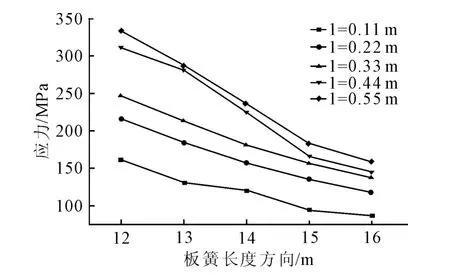
图4 中心截面纵向某处不同厚度下的应力曲线
2.4 厚度比对变截面钢板弹簧应力分布的影响
图5揭示了厚度比对钢板弹簧应力分布的影响.可以看出,当γ=0.3时变截面区域的应力平缓更加接近与“n”形,而当γ=0.6时沿长度方向的应力有比较大的差值.这说明γ值越小,钢板弹簧应力分布越均匀.原因可以解释为,γ值越趋近于1钢板弹簧越趋近于等厚度的钢板弹簧,而等厚钢板弹簧应力分布不均匀.从图5中还可以看出,当γ=0.3时钢板弹簧与其他γ值相比差异很明显,而随着γ值增大,相近的两个γ值之间的应力分步趋势逐渐变得相近.像γ=0.5与γ=0.6的钢板弹簧的应力分布的趋势就十分接近.同时,可以看出随着根部厚度的增大,不同厚度比的钢板弹簧的应力分布趋势也逐渐趋于一致.


图5 不同厚度比下的钢板弹簧应力分布曲线
3 优化验证
3.1 模型建立
利用厚度的改变来优化一个变截面钢板弹簧的总成.这里建立一个3片等宽变截面钢板弹簧总成的1/2模型.钢板弹簧应力分析是一个接触问题分析,所以板簧在有弧度部分要相互施加接触,板簧中间平直段部分与垫片之间要加接触.三片钢板弹簧的厚度与厚度比一样,均为γ=0.5,h1=6mm,h2=12mm.钢板弹簧材料为60Si2Mn,每片板簧之间有塑料垫片,模型如图6中所示.

图6 变截面钢板弹簧总成自由状态
3.2 约束条件及载荷
钢板弹簧的应力组成是由装配过程和加载过程所得应力叠加而成.所以要先模拟钢板弹簧装配过程,之后在装配过程的基础上施加载荷.
装配仿真就是要模拟中心螺栓拧紧的过程.定义第一片板簧上表面中央部分垂直位移为0;其他各片板簧和垫片约束除装配方向外的位移;第三片板簧上表面中央部分施加装配方向的位移,位移的大小为各板簧之间或板簧与垫片之间间隙的总和.板簧两端不施加约束,让其自由变形.
装配完成之后,分10个载荷步逐级加载.这样可以减小计算收敛的难度,提高了收敛的速度.
3.3 钢板弹簧总成应力分布
由图7可见,3片钢板弹簧从上至下,第一片与第二片钢板弹簧应力分布趋势相近,相比于第三片钢板弹簧,应力分布比较均匀.第三片所受应力最大.

图7 3片钢板弹簧的应力分布曲线
3.4 优化参数
为使各片应力更加均匀,三片厚度比取一个相对小的值.第三片由于应力分布最不均匀且所受应力最大,所以根部厚度取大.最终各片厚度与厚度比如表1所示.

表1 优化后各片的厚度与厚度比
3.5 优化前后各片应力分布的对比
优化前后钢板弹簧应力分布曲线的对比见图8.

图8 优化前后钢板弹簧应力分布曲线的对比
由图8可见,优化后应力分布有明显的改善.第一片与第二片钢板弹簧不但应力分布较之前更为均匀,各点的应力值也减小了.优化后与未优化的2条应力曲线交与一点,交点前优化后的应力稍大,交点后优化后的应力要小于为优化的模型.优化后第三片钢板弹簧应力变化的趋势要平缓很多,即应力分布更为均匀.从总体上看,每一片钢板弹簧应力分布都较未优化前均匀,可以判定优化达到了效果.
4 结 论
1)变截面钢板弹簧受载后,厚度方向应力表现为中间最小两 边最大.沿长度方向应力分布较为复杂,有快速上升、平稳变化、快速下降三个区域,应力分布大致呈现一个“n”形.
2)在相同的厚度比的情况下,厚度大小会影响到变截面钢板弹簧的应力分布,厚度越大,应力分布曲线越是趋近于一条直线,这也说明了大厚度的变截面钢板弹簧应力分布均匀.同时,厚度越大,在同样大小的载荷下钢板弹簧的应力值也越小.但是实际中受到成本及加工难度等因素,要选择合适厚度的变截面钢板弹簧.
3)在相同的根部厚度情况下,对比不同厚度比的钢板弹簧的应力分布.厚度比γ越小,钢板弹簧应力分布越均匀.但γ值较大时,γ值对钢板弹簧应力分布的影响减弱.由于钢板弹簧需要一定的强度和刚度,γ值的选取不宜过小.
4)对变截面钢板弹簧总成,适当的改变钢板弹簧的厚度与厚度比是可以使各片的应力分布得以优化,更加接近等应力梁.
[1]秦志敏,潘宇臣.变截面钢板弹簧设计计算[J].汽车工程,1995,17(2):108-112.
[2]丁 华,肖廉明,朱茂桃.少片钢板弹簧力学特性有限元分析[J].汽车工程,2009,31(9):864-866.
[3]廖林清,李常鑫,苏道奇,等.少片变截面式钢板弹簧的刚度研究[J].重庆理工大学学报:自然科学版,2013,27(5):6-10.
[4]吴 娜,张士强.少片变截面弹簧有限元分析[J].科学技术与工程,2012,12(34):9435-9437.
[5]TANG YingShi,CHAI Tian,HE JinJun,et al.Analysis of stiffness of taper leaf spring based on contact friction[J].Journal of Central South University:Sci-ence and Technology,2009,40(3):694-698.
[6]ZHOU Shuiting,HONG Wuhuang,OUYANG Liange,et al.Analysis and computation of taper leaf spring based on FE contact analysis[J].Advanced Materials Research,2013,705:516-522.
[7]罗志龙.少片变截面弹簧设计最大应力点的选择[J].汽车科技,2008(4):34-36.
[8]MOON Il-Dong,YOON Ho-Sang,OH Chae-Youn.A flexible muti-body dynamic model for analyzing the hysteretic characteristics and the dynamic stress of a taper leaf spring[J].Journal of Mechanical Science and Technology,2006,20(10):1638-1645.
[9]NIGRO N J,BHATIA S P.Equivalent one-dimensional system for analysis of taper leaf spring[J].Journal of Engineering for Industry,1976,98(1):39-42.
