用摆演示刚体的平动和平面平行运动

罗 宏

（苏州科技学院 数理学院，江苏 苏州215009）

1 引 言

关于刚体或质点系有很多的讨论，文献［1-2］讨论了通过实验来演示在平面平行运动（滚动）的情况下，转动惯量等参量对刚体运动的影响.文献［3-4］则讨论了刚体的平动及动点动量矩定理.但是比较刚体的平动和平面平行运动的相关文献很少.了解刚体的平动和平面平行运动的区别可以帮助学习者的思维方式由质点情况向刚体情况进展.

在相同倾角的斜面上，无摩擦下滑的刚体（平动）比作纯滚动刚体（平面平行运动）的质心加速度更大，经过相同的距离耗时更短.但由于摩擦力的存在，在斜面上演示这一现象效果不好.本文设计了2种类似的摆，摆长和悬挂的刚体都相同，只是悬挂其上的刚体分别作平动和平面平行运动（运动形式不同）.通过这2种摆，可以演示刚体的平动和平面平行运动，并进一步通过测量这2种摆的周期，比较运动形式的不同带给观测量的影响.平面平行运动与平动的主要区别是，前者有绕质心的转动而后者无.通过这一比较，可以让学生直观地了解随刚体内部运动维度的增加（刚体绕质心的转动），所观测到的物理量（周期）的变化.是否具有内部的转动维度，是刚体和质点的一个重要区别.由于作平动的刚体可以等效为质点［5］，通过该演示实验，也可以帮助学生更好地理解刚体运动和质点运动的区别，及其带来的影响.

理论计算部分，可以选择牛顿第二定律、能量法［6］或拉格朗日方程.当体系约束增加时，用能量法或拉格朗日方程处理问题会更简单（如在以下的两摆中）.另外，随着物理学习的深入，越来越多的问题需要用能量的观念来思考，所以本文选择拉格朗日方程来计算和分析.以下的讨论将只考虑摆在竖直平面内的摆动，并假设摆动的角度很小.

2 2种摆的设计和理论分析

2.1 摆1

2根长度同为l的不可伸长轻细绳（质量可忽略），对称地系于匀质细杆质心（中点）C的两侧.两绳的另一端以相同的距离系于悬挂处.细杆长度为d、质量为m.如图1所示，O点为两悬挂点的中点，OC＝l为摆长.将摆拉开小角度，由静止释放摆，摆将往复摆动.由于两绳的约束，细杆将始终处于水平状态，细杆的运动为平动.对于刚体的平动，可以将整个刚体的运动简化为质心的运动［5］，此摆可以简化为绳OC末端悬挂质点m的单摆，其周期即单摆周期.但为了便于与摆2比较，仍旧写出其动能及拉格朗日函数.

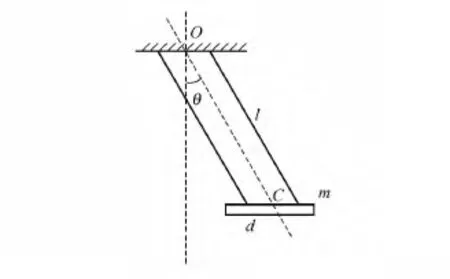
图1 摆1

由克尼希定理知，对于刚体的平动运动，系统的动能只有质心动能：

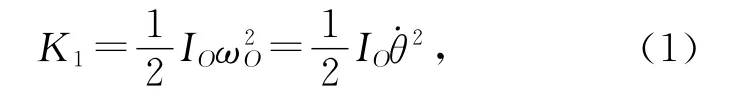
式中，IO＝ml2为细杆质心绕O点转动的转动惯量，ωO为质心绕O点转动的角速度，θ为摆角.系统的势能为

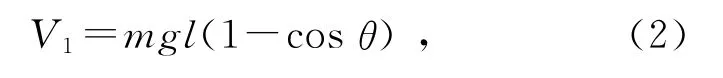
此系统为理想约束下的保守系统，则系统的拉格朗日函数为

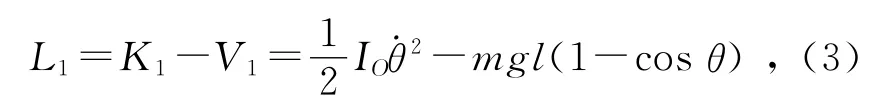
建立并解得拉格朗日方程可知，摆1在小角度近似下的周期为

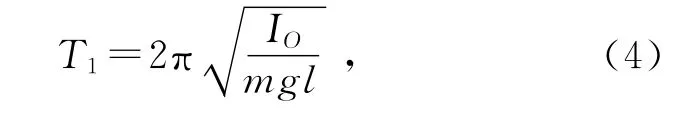
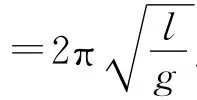
2.2 摆2

如图2所示，与摆1中相同的细杆，其两端点A和B各系1根相同长度的不可伸长轻细绳，两绳的另一端都系于悬点O，C为细杆的质心，选择两绳的长度使摆长OC＝l（与摆1相同），θ为摆角.同样地将摆2拉开一个小角度，由静止释放，摆将往复摆动，由于两绳的约束，细杆的运动为平面平行运动，可以分解为质心运动和细杆绕质心的转动.

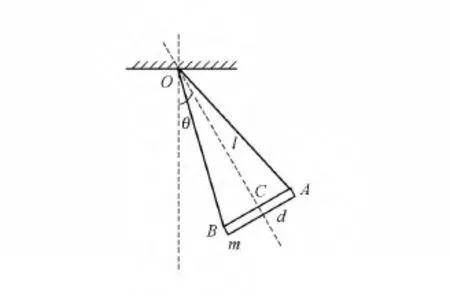
图2 摆2

细杆质心绕O点转动的角速度ωO与细杆绕自身质心转动的角速度ωC相同.这可以通过图3得知.图3中，AB为当摆角为θ时细杆的位置，A′B′为当摆角为0时，细杆的位置（经过平移使质心重合），由图容易证明当整个摆摆动的角度为θ时，细杆转动的角度也为θ，也就是说

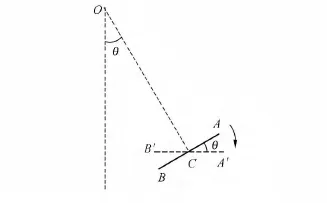
图3 细杆绕质心的转角和摆角的关系

则由克尼希定理，在摆2中细杆的动能为

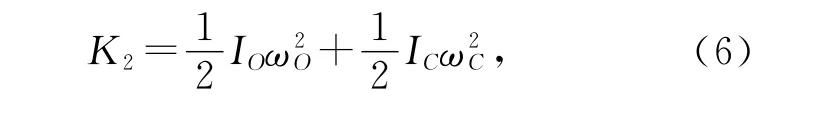
式中第一项为质心绕O点运动的动能，IO为质心绕O点的转动惯量，此项与摆1相同.第二项为细杆绕自身质心转动的动能，IC为细杆绕质心的转动惯量为

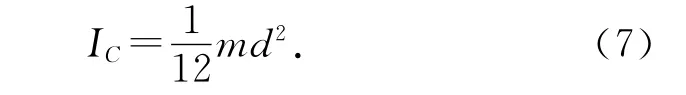
摆2的势能与摆1相同V2＝V1.此系统为理想约束下的保守系统，由式（2），（5），（6），其拉格朗日函数为

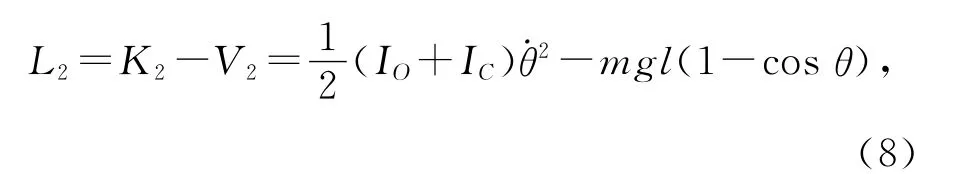
拉格朗日方程为

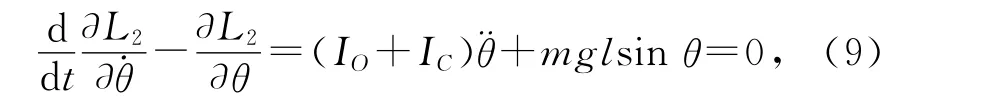
在小角度近似下，化简得到：

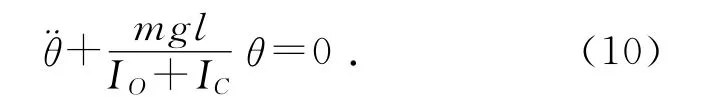
此式为谐振动方程，可得摆2的周期为

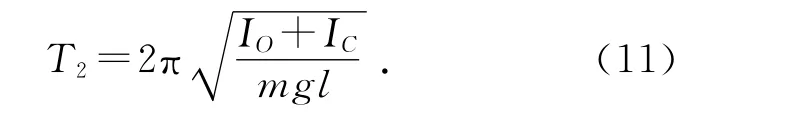
比较（4）式与（11）式，可见这2种摆的周期不同，（11）式中多出了IC项.通过对比可以发现，这2种摆的摆长（质心C到悬点O的距离）和悬挂的刚体都相同，不同之处在于所悬挂刚体的运动形式，这导致其动能组成不同.如果比较二者的拉格朗日函数（3）和（8）式，可以看出，二者拉格朗日函数中动能项有差异.在摆1中，悬挂在摆线下的细杆作平动，质心运动可以代表整个细杆，细杆可被等效为一质点，其动能为质心运动动能.而摆2中，细杆作平面平行运动，其运动除了质心运动之外，还增加了刚体绕质心的转动这一维度，由此其动能除了质心运动动能之外，还有细杆绕质心的转动动能.正是由于2种摆动能组成的不同，最终表现出其周期的不同，（11）式比（4）式多出的IC项正源于其对应的转动动能项.

从定性的角度分析这2种摆对理解平动和平面平行运动的不同也有帮助.在摆1中，细杆作平动，势能完全转化为质心动能.而在摆2中，细杆作平面平行运动，势能除一部分转化为质心动能外，还有一部分转化为细杆绕质心转动的动能.如果以相同的摆角θ静止释放二摆，这就必然导致在相同的位置，摆2的质心速度小于摆1（由于部分势能转化为转动动能），以致摆2周期较长.正如（4）式与（11）式所示.由此，可以更进一步认为，在理想约束下的机械能守恒的摆中，随着系统运动维度的增加，其质心完成1个周期的运动所需时间有增加的趋势.

由于作平动的刚体可以被等效为一质点，平动和平面平行运动的比较，可以看做是质点和刚体的比较.增加了绕质心转动自由度上的运动，是刚体较质点的重要区别，也是摆2比摆1周期更长的原因.

3 实验及结果分析

将转动惯量IO和IC代入式（4）和（11），得到在实验中实际使用的周期表达式：

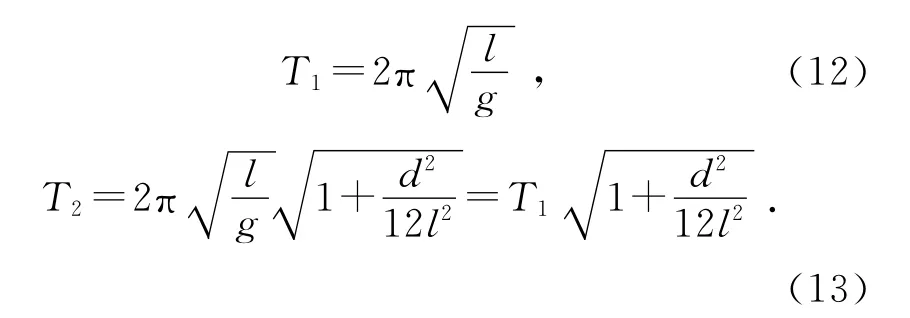
实验仪器使用常用的单摆实验仪改造而成.仪器顶部有一横梁，梁上有一小孔，悬线由小孔中穿过.摆2只需1台单摆实验仪悬挂.摆1用2台单摆实验仪悬挂，调节实验仪的高度相等，悬点间距和细杆上束缚点的间距相等即可.细杆长度和摆长分别为d＝0.615m，l＝0.300m.当地的重力加速度经查表取为g＝9.80m／s2.将以上数据代入（12）和（13）式可得10倍周期的预期值，

10T1＝10.99s，10T2＝12.77s. （14）

实验测量中，摆来回摆动10个周期测量1次时间，两种摆各测量了10次，其测量数据如表1所示.

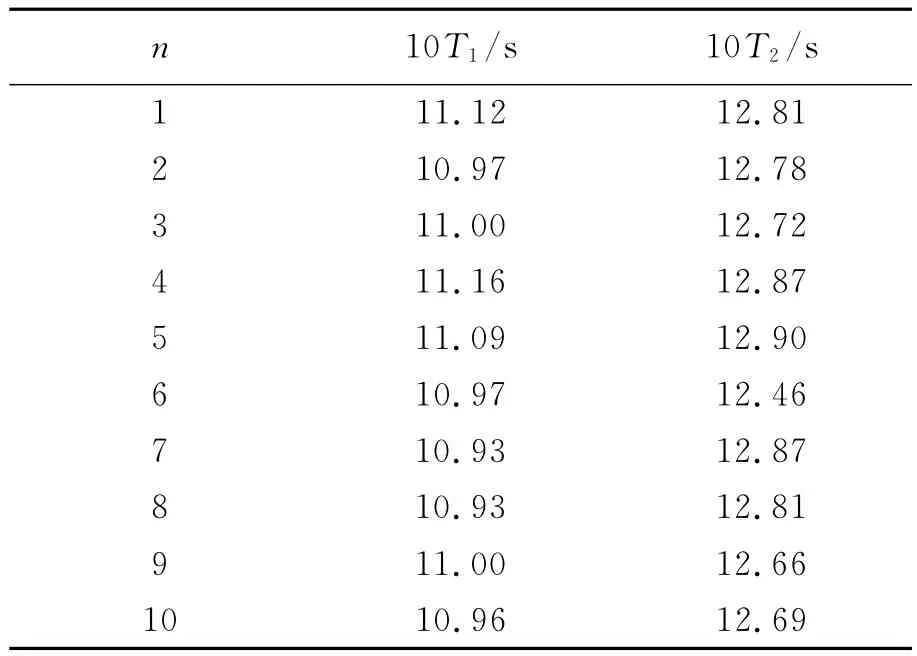
表1 周期测量数据

以下分析实验数据的不确定度，并依据实验的不确定度来给出细杆长度和摆长比例的参考范围.一种摆周期的测量结果应在另一种摆的测量结果不确定度之外，二者周期的区别才被认为是明确的.因此需合理设计摆长和细杆长度，使二摆周期的预期值有足够大的差别.

为保证2种摆周期具有可明显观察的差别，以下分析数据都会取较宽裕的值，并仍以10倍周期作为分析对象.实验中使用的秒表精度为0.01s，人的反应时间一般为0.1～0.4s之间.由于人的反应时间影响了时间测量的精度，故将B类不确定度统一取为uB＝0.4s.结合由表1得出的A类不确定度，可得2种摆10倍周期的合成不确定度u＝0.4s.则2种摆周期的预期值之差应该大于2u，为增大二者区隔取其值为1s.根据实验数据，则可得到如下不等式，

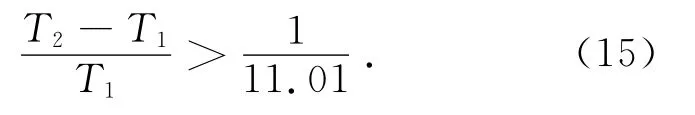
将（12）和（13）式代入计算可得

因此建议实际制作此演示实验仪时须满足（16）式的条件.如果采用文献［7，8］中所使用的较高精度的实验仪器，则此比值可以更小，但要依据实际的不确定度来分析.

4 结束语

设计了2种不同的摆，其摆长相同，所悬挂刚体相同，但刚体的运动形式不同.通过这两种摆，演示了刚体平动和平面平行运动，及其对摆周期的影响.正是摆2中刚体作平面平行运动所具有的绕质心的转动分量，使其摆动的周期较摆1更长.通过实验验证，这2种摆制作较为简单，演示效果良好.虽然实验中2种摆都悬挂了刚体，但其也可以等效作为演示质点和刚体区别的演示实验装置.

［1］古丽娜尔，朴景灿，刘秉正.滚动演示实验［J］.物理实验，2004，24（3）：41.

［2］路峻岭，汪荣宝.几种演示影响刚体滚动因素的物理实验仪［J］.大学物理，2004，23（6）：40-42.

［3］梅凤祥.关于对动点的动量矩定理——理论力学札记之八［J］.力学与实践，2011，33（3）：67-69.

［4］朱仁贵.对动点的动量矩定理在刚体平动中的应用［J］.力学与实践，2013，35（1）：80-82.

［5］周衍柏.理论力学教程［M］.3版.北京：高等教育出版社，2009：117.

［6］车立新.单摆周期的能量方法求解［J］.松辽学刊（自然科学版），2002（1）：66-67.

［7］秦鸣雷，肖一凡，杨海亮，等.大角度下阻尼对单摆摆动周期的影响［J］.物理实验，2012，32（5）：42-45.

［8］张虹雪，程雪芹，樊婷，等.单摆摆球运动轨迹控制装置［J］.物理实验，2012，32（12）：36-38.