氢灯放电等离子体参量光谱诊断

孙殿平，戚小华，王春梅，沈国土

（华东师范大学 物理系，上海200062）

1 引 言

氢灯是实验室常见设备，其主要发光机制是交流放电产生等离子体，其中处在激发态的粒子（原子、分子和离子）跃迁到基态而发射光子.等离子体是 “物质第四态”，等离子体诊断是物理学研究的重要课题之一.常用的诊断手段主要是光学诊断技术、Langmuir探针和质谱技术［1-3］.

光学测量方法特别适合于等离子体原位诊断，因为它不直接接触等离子体因而不会造成干扰.作为等离子体无接触诊断的一种方法，与探针测量手段相互补充，它能提供粒子组成、热力学温度和粒子能量分布等状态参量，也可以得到其中的碰撞、传能、电离、解离和输运等微观物理过程的信息，还可以获得物种转化与生成、基元吸附与相变等物理化学过程的基本规律，同时还能得到时间和空间分辨的信息.从实验设备上来讲，发射光谱法也是比较容易实现的.但是由于大量干扰谱峰的存在，因此在实践中这种方法主要用于简单分子的等离子体诊断.

本文利用单色仪测量得到的氢灯中氢原子和氢分子的光谱，假定等离子体处于局部热力学平衡和光学薄状态，通过计算得到等离子体电子温度、振动温度和转动温度［4］.

2 实验装置

实验装置简图如图1所示.氢灯是实验室常见设备，型号为GH-Ⅱ.单色仪为71SW301.氢灯管中氢气气压为13Pa～1kPa，氢灯电源接调压器，以便于改变放电电压.正常使用时，电压接220V，放电电压为800V（由高压探头和示波器测量），在高压交流电源的激励下，在两电极的间隙空间可形成类辉光放电，中间发出浅红的光，靠近电极发出白色明亮的光.测量时，所测辐射光来自靠近放电电极处的发光部分，将要测量的发光经透镜聚焦到光栅单色仪入口，再经单色仪分光后，由光电倍增管探测，探测信号送入计算机处理.如要测量氢灯不同放电区域的发光，可把氢灯外壳拆掉.

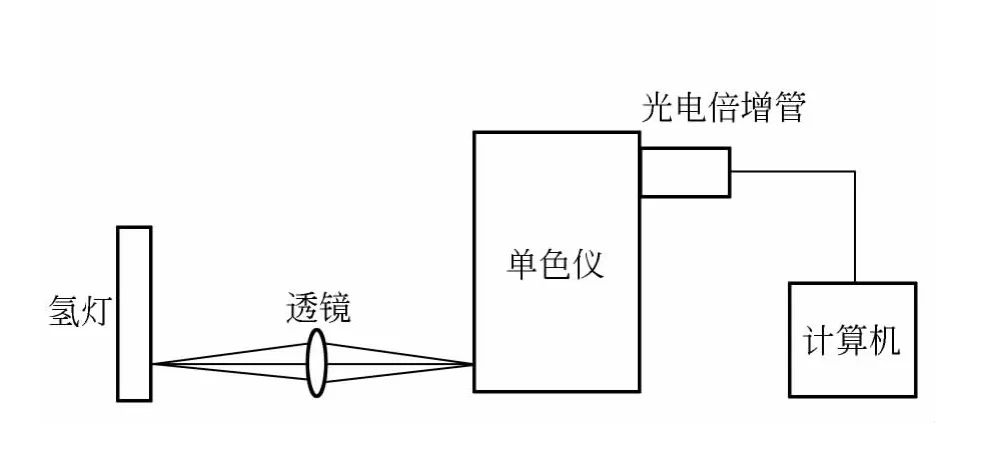
图1 实验装置图

3 实验结果与讨论

图2为实际测量的氢灯放电发光的325～675nm之间的光谱图，其中原子光谱的强度很强.图3是位于600～650nm的光谱图，主要是氢分子的d3Πu-—a3Σg＋Fulcher-α带的振转结构.实际计算时，还需要考虑测量系统的光谱响应系数［5］.

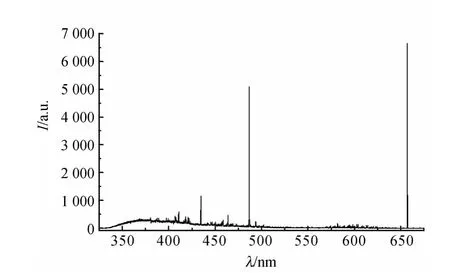
图2 氢灯放电发光的325～675nm之间的光谱图

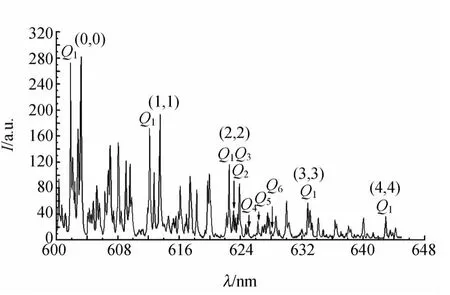
图3 氢分子d3Πu-—a3Σg＋ Fulcher-α带的振转结构光谱图

3.1 电子激发温度

等离子体的激发温度用来表征其中离子、分子和原子的激发过程的发生强度［4-5］.如果激发过程主要是由电子碰撞过程实现的，那么激发温度的变化反映了等离子体中电子能量的变化，即电子温度的高低.当处于一定激发能量范围内的激发态能级上的粒子布居数与此能量范围的电子达到碰撞激发平衡时，处于第i能级的粒子数密度ni由玻尔兹曼分布给出［4-5］：

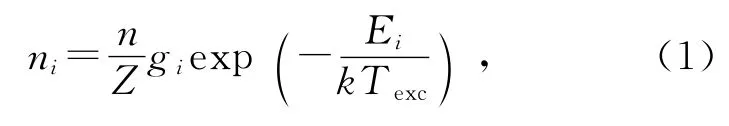
等离子体中原子发射光谱的峰强度为

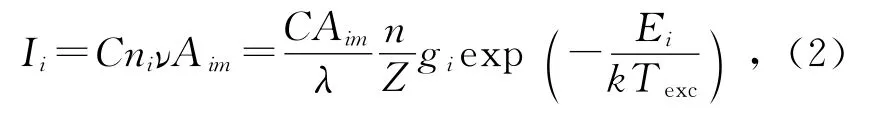
其中，Aim是i能级跃迁到m能级的自发射跃迁概率；C是仪器收集和传递常量，一般情况下可视为常量，但在空间分辨发射光谱的测量中由于仪器与辐射区相对位置的改变，C可能发生变化，如果位置改变不大，则可以视C为常量.

通过测量这些激发态粒子的光辐射强度，可以得到相应激发态的粒子数布居数之比，进而利用玻尔兹曼图解法可以得到激发温度［6-7］：

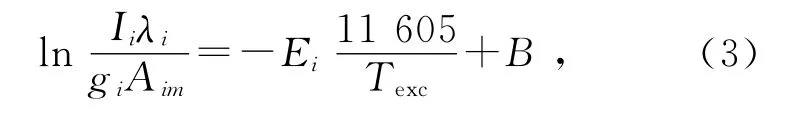
对实验数据拟合，由直线斜率可求得电子激发温度Texc.

为了计算氢气等离子体的激发温度，从光谱中选取H的巴尔未系谱线，其光谱学参量见表1.

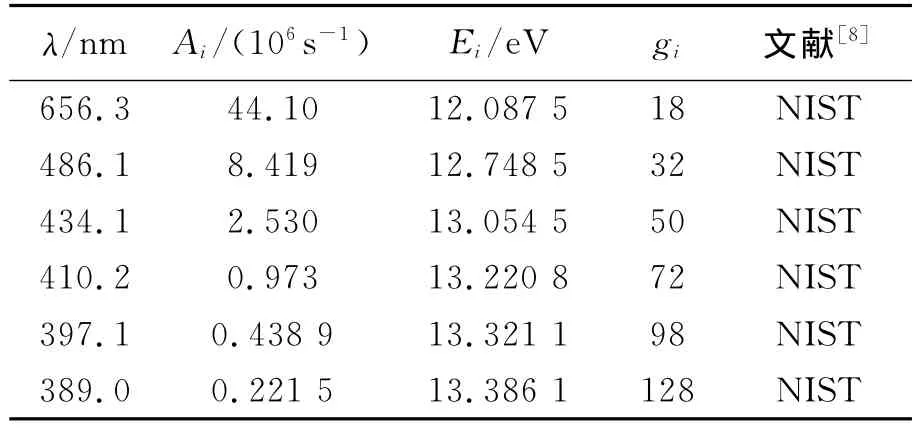
表1 选定HⅠ谱线的光学参量

根据氢气放电发射光谱强度和表1的光学参量，以ln（Iiλi／giAi）为纵坐标，Ei为横坐标画出玻尔兹曼曲线如图4所示，然后对曲线进行线性拟合，拟合直线的斜率m＝-11 605（eV-1·K-1）／Texc＝-2.234 21，由此求得电子激发温度Texc＝（5 194±350）K.

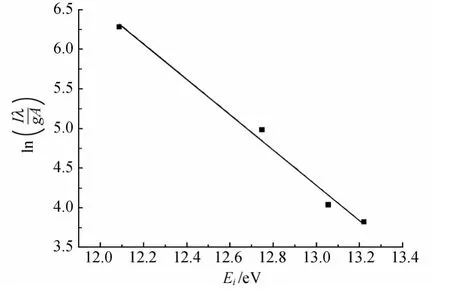
图4 氢原子发射光谱的玻尔兹曼曲线

作图中的光谱强度根据系统响应系数和玻璃管材料的透射系数作了修正，由于397.1nm和389.0nm较小，实验中未被采用.

激发温度和电子温度在平衡态下数值相等，但在热力学非平衡态下激发温度和电子温度是不相等的［4］.

3.2 转动温度

分子气体温度不太高时会激发转动自由度.分子布居数按玻尔兹曼分布，处于给定的转动能级.双原子分子振转谱线发射强度测量法是一种传统的测量等离子体转动温度的方法.转动温度Trot可通过测量R，P或者Q支的各条谱线的发射强度I，并将其作为转动能级能量E的函数做曲线的方法求得［9-10］：

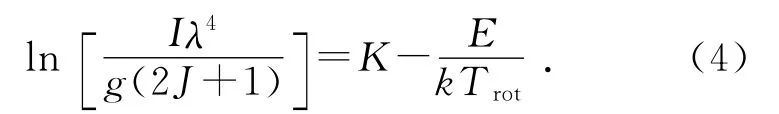
式中，λ是跃迁波长，Trot即为转动温度，g是核自旋统计权重.E是上能级的转动能量［4］：

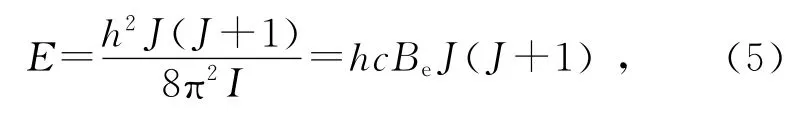
式中J＝1，2，…是转动量子数，I是分子转动惯量，Be＝是转动常量（cm-1）.

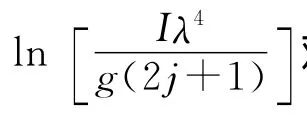
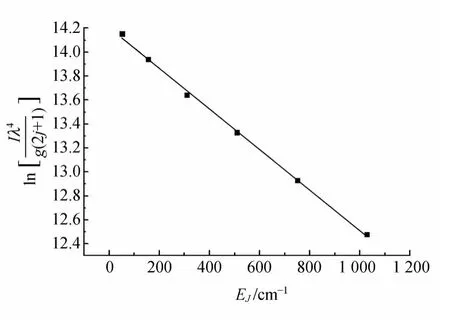
图5 氢分子放电Fulcher-α带（2，2）Q 支发射光谱的玻尔兹曼曲线

3.3 振动温度

在局部热平衡条件下，H2激发态的各振动能级的粒子数密度，遵循玻尔兹曼分布规律［10］，即：

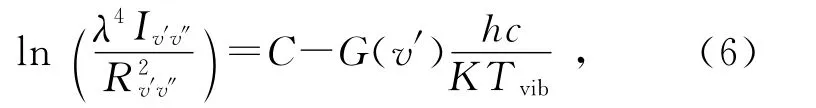
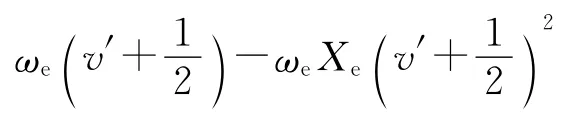
同样，利用图4的数据和（6）式拟合直线，如图6，m＝-1／（0.695Tvib）＝-0.000 219 4，得到H2激发态的振动温度为Tvib＝（6 560±450）K.

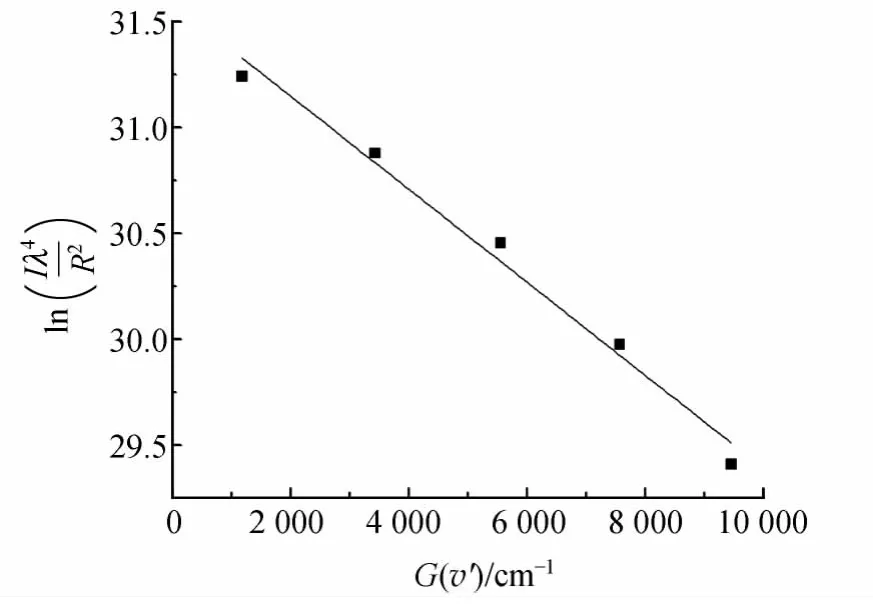
图6 氢分子放电光谱Fulcher-α带的振动带玻尔兹曼曲线

4 结 论

在实验所测的氢等离子体光谱中，氢原子的巴尔未系谱线最明显，可以将巴尔未系谱线作为特征谱线，由此谱线的强弱可以定性地表征活性氢原子的多少，由氢原子巴尔未系的光谱强度的变化趋势可以表征等离子密度的变化.由氢分子Fulcher-α带光谱，根据玻尔兹曼图解法拟合计算氢分子振动温度和转动温度，了解振动能级粒子数分布，及由转动温度得到气体温度.

［1］赵化侨.等离子体化学与工艺［M］.合肥：中国科技大学出版社，1993：1-38.

［2］孙殿平，朱轶，杨晓华，等.离子分子束源的浓度调制光谱研究［J］.光谱学与光谱分析，2006，26（9）：1594-1598.

［3］任兆杏，丁振峰.低温等离子体技术［J］.自然杂志，1996，18（4）：201-205.

［4］辛仁轩.等离子体发射光谱分析［M］.北京：化学工业出版社，2005：102-136.

［5］孙殿平.等离子体喷束及其光谱诊断的研究［D］.上海：华东师范大学，2008.

［6］赫兹堡G.分子光谱和分子结构（第一卷）［M］.北京：科学出版社，1983：153-163.

［7］Crosswhite H M.The hydrogen molecule wavelength table of Gerhard Heinrich Dieke［M］.New York：Whiley，1972.

［8］NIST.http：／／physics.nist.gov／cgi-bin／ASD／lines1.pl.

［9］Xiao Bingjia，Kado S，Kajita S，et al.Rovibrational distribution determination of H2in lowtemperature plasmas by Fulcher-αband spectroscopy［J］.Plasma Phys.Control.Fusion，2004，46：653-668.

［10］Fantz U，Heger B.Spectroscopic diagnostics of the vibrational population in the ground state of and molecules［J］.Plasma Phys.Control.Fusion，1998，40：2023-2032.

［11］Kajita S，Kado S，Uchida N，et al.Measurements of hydrogen negative ion and its comparison with the molecular hydrogen spectra in divertor simulator MAP-II［J］.Journal of Nuclear Materials，2003，316：748-753.