弗兰克-赫兹实验的计算机模拟

邹 莹，姚 志，姜东光，孙继忠

（大连理工大学 物理与光电工程学院，辽宁 大连116024）

1 引 言

在物理学发展史上，弗兰克-赫兹实验举足轻重.此实验无可争辩地验证了玻尔的量子理论——电子处于不连续的能级上.弗兰克和赫兹由于在这方面的杰出贡献获得了1925年的诺贝尔物理学奖［1］.

1914年，即玻尔理论发表的第二年，弗兰克（F.Franck）和赫兹（G.Hertz）进行了电子轰击原子的实验，在充汞的放电管中发现：透过汞蒸气的电子流随电子的能量呈现有规律的周期性变化，间隔为4.9eV，证实了原子内部能量是量子化的，为玻尔发表的原子理论提供了坚实的实验基础［1］.目前，该实验也是许多高校物理教学中的基本实验.早期的弗兰克-赫兹实验都是用电子轰击汞原子，但是因为汞蒸气有毒，而且常温下汞为液态汞管加热困难，因此，人们在实验中选择了用氩气替代汞蒸气［2］.但是在长期的实验过程中，人们还是发现了许多实验结果与理论分析方面的偏差.本文将介绍笔者编制的蒙特卡罗仿真程序及其原理.该程序可理论再现弗兰克-赫兹实验中电子与氩原子的相互作用过程，定量评估碰撞、运行参量对结果的影响.一方面，此模拟程序可以用来解决学生的疑惑，加深对量子能级概念的理解，另一方面可以为改进实验方案提供理论指导.

20世纪中叶，计算机的出现使数学方法模拟复杂的实验成为可能.在这种情况下，蒙特卡罗方法作为一种可行的而且是不可或缺的计算方法被提出，并迅速发展起来［3-4］.蒙特卡罗方法受问题条件限制的影响小，容易处理带有大量碰撞的问题，特别是各向异性散射问题，提供的物理信息较为丰富.该方法在电子与固体相互作用、基本粒子理论、晶体生长等领域中的研究都得到了成功的应用.近年来，蒙特卡罗方法很适合模拟阴极区的电子运动［5］，诸多大气压放电的模拟过程中都使用了该方法［6］.

2 实验简述

图1中，K为阴极，VG1K为正向电压，VG2K为加速电压，VG2A为减速电压.电子由阴极发出经电场VG2K加速趋向阳极，只要电子能量能够克服减速电场VG2A，就能穿过栅极G2到达极板A形成电子流.由于管中充有气体原子，电子前进的过程中要与氩原子发生碰撞，按照量子力学的观点，氩原子对于外来的能量，不是“来者皆收”，而是当外来能量达到激发阈能时，它才吸收，即氩原子内存在能量分立的量子态.在电子能量低于激发阈能的情况下，电子能量越高，就越容易到达极板的A极，电流也就越来越大.如果电子能量达到或超过激发阈能时，电子将有可能把相应的能量传给氩原子，如果电子在到达栅极G2时，能量不足以克服反向电压，那么电子将不会到达极板，因此电流大幅降低.由于原子内部能量是量子化的，这样得到极板的电流会随着加速电压变化而呈现周期性的变化.

图1 弗兰克-赫兹管实验装置图

3 数值模拟方法

本文采用蒙特卡罗方法，直接模拟了从阴极发射的电子在电场的作用下的运动.气体的温度比较低，可假设原子是静止的，只存在轴向电场，在2次碰撞间的电子运动轨迹处在同一平面内.采用位置空间一维，速度空间三维的模型，求解牛顿运动方程，

在推进过程中，根据电子与原子的碰撞截面，通过抽样产生一系列随机数来确定电子与原子是否发生碰撞；如发生碰撞，判断碰撞的位置、类型及碰撞前后电子的速度变化.在1个时间步长内，第κ种类型的碰撞概率为

这里σtot为碰撞总截面，ε为带电粒子能量，v为粒子的运动速度，Nneutral为背景气体中性粒子密度，在本文中即氩原子密度为

其中p为气体压强，单位为Pa；T为气体温度，单位为K；KB为玻尔兹曼常量.判断粒子运动1个时间步长Δt后是否可以发生碰撞，可由式（3）中所求得的概率p决定.取随机数R，若R＞p，则不发生碰撞；否则，若R＜p，粒子发生碰撞.

若带电粒子发生碰撞，则需要判断发生何种类型的碰撞，首先应得到粒子具有能量ε时的各种碰撞的总截面以及各种碰撞对应的截面，以确定每种碰撞所占的概率，然后取1个在［0，1］上均匀分布的随机数R，R所在的区间即决定了它的碰撞类型.图2所示即为电子与氩原子碰撞截面数据.只考虑了3个电子激发态，因为更高能级的碰撞截面相比非常小，可以忽略.同样的道理，也只考虑了第一电离态.

图2 电子与氩原子碰撞截面图1

在氩气中，对于电子与中性粒子的碰撞，只考虑3种类型碰撞，即弹性碰撞、激发碰撞和电离碰撞.其碰撞截面分别为σela，σexci，σion，总的碰撞截面为σtot.判断碰撞类型的具体过程如下：

a.取随机数R.

b.R 同σela／σtot相比较，若R＜σela／σtot，则发生弹性碰撞.

c.当 R＞σela／σtot，则再次产生随机数 R 同（σela＋σexci）／σtot比较；如果R＜（σela＋σexci）／σtot，则发生激发碰撞，否则继续下一步.

d.若 R＞ （σela＋σexci）／σtot，则 发 生 电 离 碰撞［6］.

发生弹性碰撞、非弹性碰撞，电子的散射角χ和方位角φ 由（5）～（6）式确定：

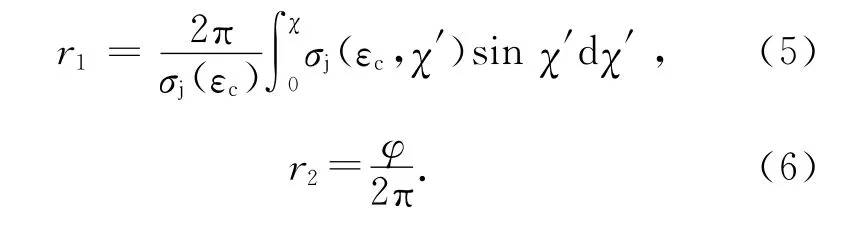
式中σj（εc，χ′）是微分截面，电子速度与x轴夹角的余弦为

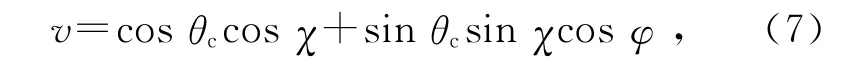
其中θc为碰撞前的θ值.发生弹性碰撞、激发碰撞，散射电子的动能分别变为

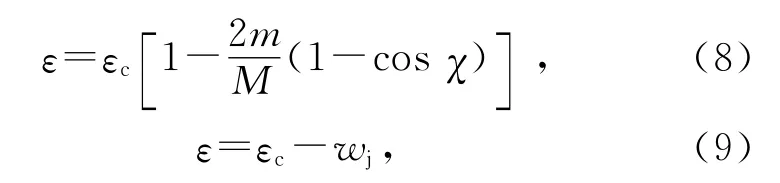
式中m／M是电子与氩原子的质量比，wj是激发阈能.分2种情况考虑发生电离碰撞后的散射、出射电子的动能变化.第一种情况，只电离出1个电子.由于无法分辨散射电子与电离产生的电子，其中任一个电子的动能由（10）式确定：

另一个电子的动能为

这里wi为电离能.第二种情况，电离出1个电子并同时使原子激发或同时电离出多个电子.这时，假设1个电子的动能为入射动能与电离能的差值，其余电子的动能为0［7］.对电离碰撞，假定碰撞前后电子的速度方向不发生变化［8］.激发过程可假设散射电子沿角向近似各向同性［9］.

模拟过程中，大量电子经过加速间隙加速，与背景氩气发生碰撞，最终被电极收集.在稳态条件下，极板上收集的电流值是根据（12）式确定：

式中SA是极板A的面积，dQ／dt是极板A上单位面积、单位时间内收集的电量，而dQ′／dt是模拟中极板A上单位面积、单位时间内收集的电量.由于模拟中跟踪的电子不能像实际中那么多但必须从统计上足够多，这样在稳态条件下，dQ′／dt一定正比于dQ／dt.dQ′／dt可以按（13）式计算，

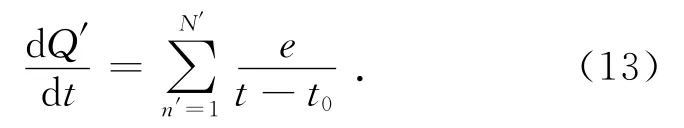
式中N′是极板上收集的电子数，e是电子的电量，t是收集时的时间，t0是起始时刻，或电子被电离产生时的时刻.

程序框架图如图3所示.

4 模拟结果与讨论

模拟参量分别为：压强为101kPa，温度为300K，平均自由程10-6m，时间步长远小于粒子的平均碰撞时间，模拟粒子数为1×105，极板电压从0变化到85V，极板宽度5cm.

图3 程序框架图

4.1 模拟结果与实验结果的比较

考虑电子与氩原子发生弹性碰撞、激发碰撞和电离碰撞，其中激发碰撞可将氩原子的外层电子激 发 到 多 个 激 发 态，包 括 4s′1／2态、3d1／2态、3d′3／2态，对应的阈能分别为11.8eV，14.1eV，14.3eV，此外，电离碰撞对应阈能为15.76eV，模拟结果如表1所示.

表1 模拟结果1

实验曲线和模拟曲线如图4所示.

图4中，横坐标表示两极板间所加的电压值，纵坐标表示无量纲化后的电流.其中，对应的实验参量分别为：电压VG2K为0～85V，灯丝电压为3.0V，拒斥电压为5.4V.

图4 实验曲线和模拟曲线

通过对比实验曲线和模拟曲线，发现2种方法得到的结果符合很好.同时，也可以通过模拟过程合理地解释实验过程，电子在2个极板间受到加速电场的作用而前进，在前进过程中将与背景气体氩原子发生碰撞，包括弹性碰撞、激发碰撞和电离碰撞.若电子与氩原子发生弹性碰撞，因为电子的质量远远小于原子的质量，所以几乎没有发生能量的转移，即电子不损失能量，但是弹性碰撞可能会改变电子运动的轨迹，导致电子往复运动进而增加电子与背景气体的碰撞次数.当极板间电压值达到或超过氩原子的第一激发电位时，电子与氩原子发生非弹性碰撞，包括激发碰撞和电离碰撞.其中，由于氩原子内部存在一系列激发量子态，因此若电子的能量达到一定值时，可能使氩原子受激到更高的激发态；同时电子也有可能使氩原子发生电离碰撞.当发生激发碰撞和电离碰撞时，电子将损失相应的阈能，导致电流迅速下降.除此之外，电子在前进过程中也可能并不与氩原子发生碰撞，即不损失能量，直接到达极板的另一端.最终，到达极板A上的电子将对电流值做出贡献.随着极板间电压的增大，到达极板的电子数越来越多，所以电流整体成上升趋势.

在图4中，实验曲线和模拟曲线略有差别，这是因为模拟和真实实验条件并不完全相同.例如，装有背景气体氩气的管内气体压强数值不具体，只能近似认为101kPa；电子从阴极发射出来速度是随机分布的，在模拟中近似认为电子的初始速度符合麦克斯韦分布.同时，实验本身存在着系统误差，而且测量也存在一定的误差，这些因素都会导致模拟结果和实验结果存在差别，但是并不影响总体趋势和物理规律.

4.2 探索峰间距变大的因素

从实验和模拟结果曲线可以发现它们的峰（谷）间距并不完全相等，为了探究造成这种现象的因素，另外考虑了以下2种电子与氩原子发生碰撞的模型：

1）假设电子与氩原子发生弹性碰撞，只发生从氩原子基态到第一激发态（4s′1／2态）间的激发碰撞（对应的阈能为11.8eV）和电离碰撞.

2）假设电子与氩原子只发生弹性碰撞和激发碰撞，不发生电离碰撞.

模拟结果分别如表2～3所示.

表2 模拟结果2（电子与氩原子发生弹性碰撞，激发碰撞和电离碰撞）

表3 模拟结果3（电子与氩原子发生弹性碰撞和激发碰撞）

利用表1～3中的模拟数据可以做出弗兰克-赫兹实验曲线中峰值间隔与峰值个数的关系图（见图5），其中直线为用最小二乘法得出的拟合曲线.

图5 峰间距变化的线性拟合曲线

从拟合曲线不难看出，当不考虑电子与氩原子发生电离碰撞时，峰间距变化不显著；而考虑电离碰撞同时考虑电子激发碰撞时，分别假设电子碰撞氩原子使其最外层电子只能激发到第一激发态（见表2）和可能激发到多个激发态时，峰间距变化趋势几乎相同（见表1）.可见，电子与氩原子发生电离碰撞是影响峰间距变化的主要因素.

同时，通过对表1中的数据拟合曲线进行外推，易得到该曲线与纵轴的截距约为12.1V.对应电子在电场中获得能量为12.1eV，与理论上氩原子最外层电子跃迁到第一激发态所需的电压值11.8eV非常接近.

4.3 关于电子与氩原子碰撞截面的讨论

结合本实验中的实验条件，计算出了极板间电压在0～85V之间时电子的弹性碰撞和非弹性碰撞的截面图，如图6所示.

图6 电子与氩原子碰撞截面图2

当电子的能量达到激发碰撞和电离碰撞的阈能时，其中激发碰撞截面和电离碰撞截面随着极板间电压的增大而增大，发生激发碰撞和电离碰撞的概率也相应地增加.同时不难发现，对于激发碰撞而言，显然电子被激发到第一激发态的碰撞截面概率较大，被激发到其他激发态的碰撞截面概率非常小.通过图6的曲线趋势，发现随着电子能量增加，电离碰撞截面逐渐比激发碰撞截面大.因为电离碰撞的阈能比激发碰撞阈能大，所以电离碰撞起的作用越来越大.如果电离碰撞起的作用过大，将影响测量氩原子的第一激发电位，因此在实验中要尽可能地避免电离碰撞所起的作用，所以尽量在电压不太高时进行多次测量.

4.4 程序的其他功能

该计算机程序还可以用于模拟探究弹性碰撞在这一物理过程中所起的作用.例如，虽然弹性碰撞使电子损失的能量很小，但是弹性碰撞可能改变电子的运动方向和轨迹，进而导致碰撞次数的变化.我们的程序可以很好地追踪电子运动的轨迹，深入探究弹性碰撞在这一实验过程中所起的作用.除此之外，还可以探究在这一物理过程中温度、压强等因素对实验的影响，为实验工作提供合适的参量支持.

5 结 论

运用蒙特卡罗数值方法，考虑了实际弗兰克-赫兹实验中的各种物理过程，建立数值模型，并编制了相应的模拟程序.选择与实验对应的输入参量，用本程序可以得到与实验的实际测量数据定量一致的数据.配合实验数据，此程序可以帮助教师形象地解释电流-电压曲线的许多难以理解的问题，例如电流幅值为什么随着加速电压增加迅速上升？为什么电流峰值间距间对应的电压差值随着加速电压增加有变大的倾向？此仿真程序可以帮助学生加深理解弗兰克-赫兹实验中的各种物理过程，如弹性碰撞起多大作用，如何起作用？为什么？电离碰撞起多大作用，对实验的误差起什么作用？这些过程的正确理解可以进一步帮助学生接受量子能级概念.另外，利用此程序还可以帮助优化实验条件，设计更合理实验途径.

［1］杨福家.原子物理学［M］.北京：高等教育出版社，2002：56-60.

［2］詹卫伸，丁建华.物理实验教程［M］.大连：大连理工大学出版社，2004：206-209.

［3］Metropolis N，Ulam S.The Monte Carlo method［J］.J.Am.Stat.Assoc.，1949，44（247）：335-341.

［4］Metropolis N，Rosenbluth A W，Rosenbluth M N.Equation of state calculations by fast computing machines［J］.J.Chem.Phys.，1953，21（6）：1087-1092.

［5］Sun J Z，Gong Y，Wang D Z.Monte Carlo simulation of electrons in the cathode region of a glow discharge in the argon［J］.J.Phys.D：Appl.Phys.，1993，26：436-441.

［6］Vahedi V，Surendra M.A Monte Carlo collision model for the particle-in-cell method：applications to argon and oxygen discharges［J］.Comput.Phys.Commun.，1995，87（1-2）：79-198.

［7］孙继忠，宫野，王德真.氩气直流辉光放电阴极区电子群 的 蒙 特 卡 罗 模 拟 ［J］.Chinese J.Comp.Phys.，1993，10（1）：87-94.

［8］Paulick T C.Electron multiplication in the glowdischarge cathode fall［J］.J.Appl.Phys.，1990，67（7）：2774-2788.

［9］Chutjian A，Cartwright D C.Electron-impact excitation of electronic states in argon at incident energies between 16and 100eV ［J］.Phys.Rev.，1981，A23（5）：2178-2193.