基于π定理推导的桩基最大地震附加弯矩计算公式

马 亢，陈东霞，牛富生，孙 庆

（1.厦门大学建筑与土木工程学院，福建 厦门361005；2.同济大学岩土及地下工程教育部重点实验室，上海200092）

建筑物（含基底桩基）建造完成后，桩基即承担一定的从上部结构传递来的竖向荷载.它是桩体几何设计和配筋的主要依据，与地震峰值加速度（PGA）、上部结构传至桩基的荷载水平、桩身刚／强度、地基土性等因素密切相关，准确确定桩基最大弯矩及分布特征对桩基抗震设计尤为关键且必要.

目前，在国内外诸多设计规范中仍未有统一明确的桩基抗震设计图表或计算依据，如我国的《建筑桩基技术规范》（TGJ94－2008）、《建筑抗震设计规范》（GB50011—2010）等，以及国外某些专业规范：如U－niform Building Code （ICBO—1997）、Eurocode（EN—1998）、Indian Seismic Code（IS1893—2002）等均未有严格意义上专门的桩基抗震计算规定.桩基抗震设计很大程度上仍采用拟静力法（如动力系数法，取静力最大设计弯矩的1.1倍作保守设计）、简化数理模型计算和其他各类地震复核方法［1－3］；或者专门针对存在液化土层中的桩基，通过折减承载力或控制液化侧扩地基变形等做法作保守设计［4－5］.显然，这些做法都是不严谨的，缺乏科学性，以致地震中桩基损毁现象屡见不鲜，在实际桩基抗震设计时也不经济.至今，关于桩－土动力相互作用的研究很多，也出现了一批有意义的成果，但绝大多数仍集中于针对上部结构的动力分析上（如桥体结构、建筑结构等），均忽视了桩基本身的抗震研究，这对低层较轻的上部结构可能影响不大，但对高层高重结构，地震时桩基与地基土的相互作用强烈，桩基自身的安全稳定性也是一个须重点关注的问题，并有待进一步规范.

作者在既往研究中［6－8］对黏性土中桩基震害破坏机制及桩－土动力相互作用机理已作较为深入地探讨，并获得一定认识.文献［6］通过离心机地震模型试验得出：地震下桩－土间动力相互作用迫使桩基产生地震附加弯矩，一定情况下（如桩基承受上部结构较重、地震强度较大时）将十分显著，在桩基配筋时须另计考虑；更因两者动力相互作用致使基础与土表运动的非一致性，两者在加速度时程、反应谱特征、周期及放大效应等方面均存在显著差异，传统结构抗震设计中采用自由场土表的地震动参数直接作为基底参数是不严谨的；文献［7］对两组刚度（EI）差异显著的桩基（EI最大相差10.5倍，以刚性桩和柔性桩区分之）开展的离心机地震模型试验及工程模拟的有限元软件ABAQUS计算得出：桩头固定的桩基，其最大弯矩发生于桩筏联结处；对于柔性桩，地震中周围土体对桩基主要为约束效应，致使桩基某个深度以下弯矩很小，可忽略不计；对于刚性桩，土体对桩基主要是施加附加惯性力作用，致使基础周期明显高于自由场土体，从而桩体在较深处弯矩仍十分显著.文献［8］通过研发黏土在地震作用下的软化降强本构模型，并串联至ABAQUS程序而计算得到的桩基弯矩规律，与试验结果基本一致.本文将以此3篇文献中既得成果及大量原始弯矩数据为基础（见表1示），继续作深入研究，对实际桩基工程中最大地震附加弯矩的设计及计算提出判据，以为工程设计施工时借鉴、采用.

1 π定理

人们在研究某一自然现象时，目标是希望能将其本质过程表达为一种定量的函数关系：

其中，x1，x2，…，xn表示与该过程有关的物理量及某些物理常数.

由于自然现象的本质是与测量单位制的选择无关的，而描述某一自然现象各个物理量的数值却与单位制有关.当函数关系式（1）改写成无量纲形式时：

它才真正反映了自然过程的本质，因为无量纲物理量的数值与单位制的选择无关.式（2）中π1，π2，…，πr是由n个变量x1，x2，…，xn组合而成的r个无量纲变量，不含任何与物理量的测量方法有关的系数.此举通过减少变量数目（r＜n），大大简化了研究工作.从式（1）到式（2）的处理过程实为量纲分析和相似性理论的方法.这个方法涉及各物理量之间存在的本质上的深刻联系，它在很多科学领域中都曾起过重大作用［9－11］.Buckingham 的π 定理是相似性原理及 量 纲 分析方法的成功应用，可简述为：对某过程具有重要性的变量数目n减去基本变量的数目m（一般取长度l、质量m和时间t，m＝3），就是独立的无量纲组合变量的数目r（＝n－m）.本文将以此为理论基础，对既往研究中取得的大量原始数据作进一步分析归纳，即导出桩基最大地震弯矩计算公式.

2 π式的确定

2.1 研究问题

对于桩基地震弯矩的研究，以Nikolaou［12］为代表的研究者作了较好的工作.Nikolaou通过对长细比为20和40的两类桩基开展的数值计算及数学分析，对双层土中单桩的最大弯矩，最早提出计算公式如下：

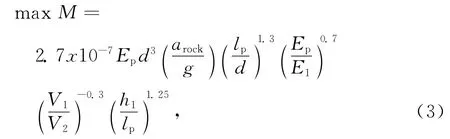
式中，arock为基岩加速度峰值，lp为桩长，d为桩径，Ep、E1分别为桩体与上层土的弹性模量；V1、V2分别为上下土层的剪切波速；h1为上层土的厚度.

由于式（1）未考虑上部结构传至桩基的荷载水平及地基域土体的惯性质量效应，后来，Nikolaou［13］经过改进又提出了一个计算公式：

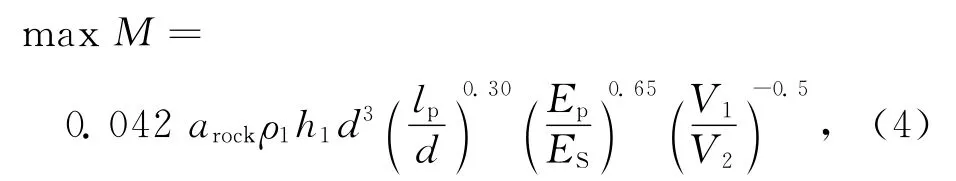
式中，ρ1为上层土体的密度，这在一定程度上考虑了地基域土体的质量（即惯性效应），是对以前工作作了重要改进，但仍未考虑从上部结构传至桩基的荷载效应.由相关研究可知，桩端所承受的荷载水平不仅对桩身弯矩峰值影响显著，而且还决定着桩（筏）基结构的自振频率，是极为重要的工程因素之一.故此，本文针对包括桩承荷载水平在内的最广泛因素作用下桩基最大弯矩开展讨论.

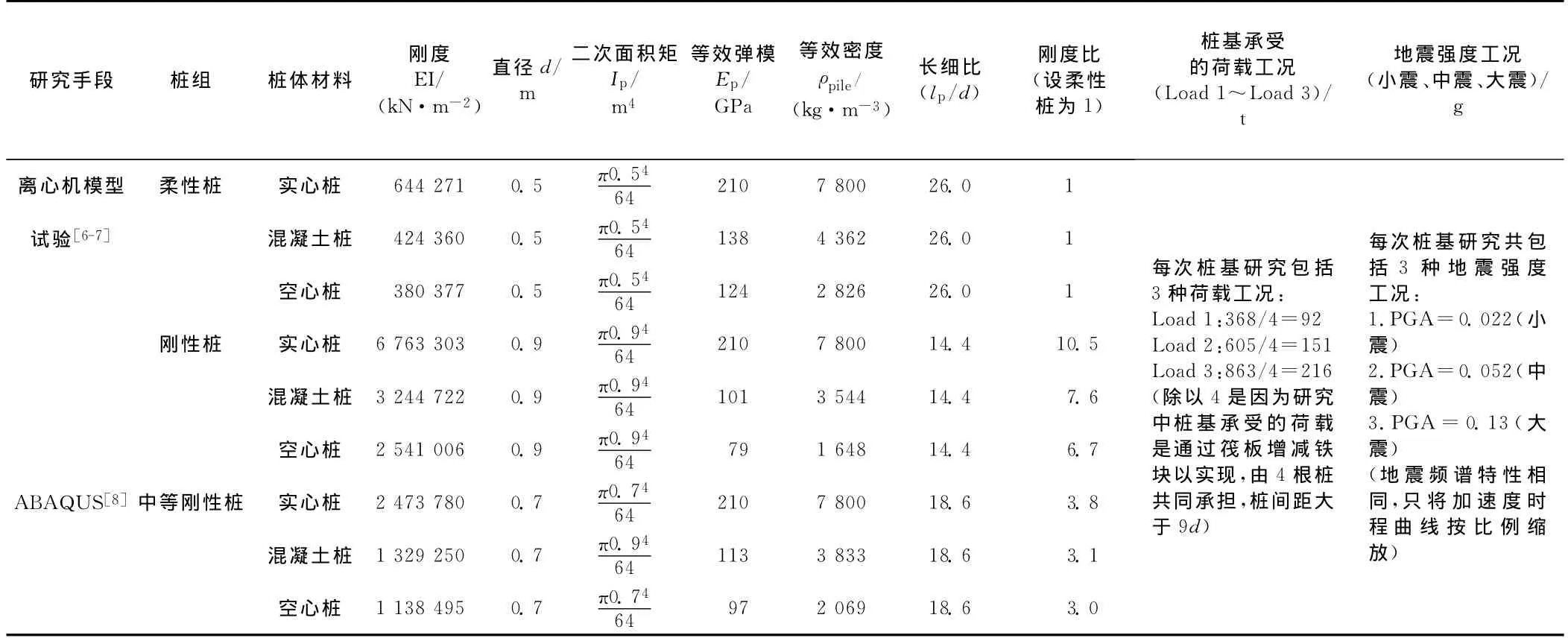
表1 已完成桩基的特性参数及研究工况Tab.1 Properties parameters and study cases of piles in finished research

本文研究的桩（筏）基型式，单一土层底部为基岩，土层厚度与桩长相等；桩底支立于基岩上，桩端承受一定的从上部结构传递的荷载（以分担筏板重量计）.这是桩－筏－土体系在地震下的动力相互作用研究的典型问题，即作者在以往研究中（试验及ABAQUS计算分析）采用的同一数理模型.影响桩身最大弯矩Mmax的因素繁多，其中最具代表性的可由式（5）表达如下：

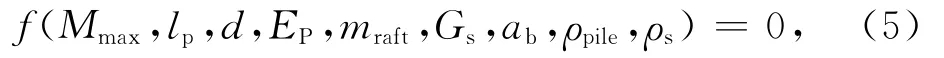
其中，最大弯矩：Mmax；桩长为lp；桩的直径为d；桩弹性模量为Ep；筏板质量为mraft；土体剪切模量为Gs；基岩加速度（输入）为ab；桩的密度为ρpile；土体密度为ρs.

2.2 π式的确定

由于式（5）中lp、mraft及ab包含有l、m、t这3个基本量纲，故选取其作为基本量.根据π定理，式（5）中9个物理量可组合成6个无量纲π式，因此，根据桩－筏结构与地基土体系各自的地震属性，及其与地震工程中各因素间的内在联系，分别提出并推导如下：

1）无量纲弯矩：

该式可由桩（直径为d和弹性模量为Ep）的应变εm（无量纲）与相应弯矩M之间的关系导得：

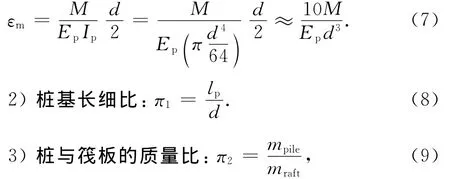
此项主要表达两者惯性质量效应之比（桩基本身质量及其所承担的从上部结构传递至筏板，并进而传递至桩端的惯性质量），即谁占主导或程度大小.由于，地震中桩基弯矩只主要发生于一定深度范围内，即可采用此深度范围（lα）桩基质量即mpile，可计为：

其中，lα可根据一个普用公式（Poulos［14］；Randolph［15］）确定：

4）桩（筏）基结构与自由场土体的自振频率之比：

当π3＝1时，即为共振效应，是工程中极力回避的.桩（筏）基结构可按单自由度系统（SDOF）考虑，在上述3）中，桩基质量已有考虑，此处视桩为无重柱，EpIp为桩体刚度，桩（筏）基结构刚度k可表达为：

其中，a为常数，其值取决于桩端约束条件.

因此，桩筏基础的共振频率可表达为：

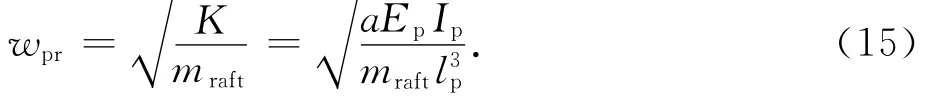
对于与桩长（lp）等厚的土体，其主周期理论解为：

其中，Vs为土体的剪切波波速，且有：

因此土体的频率为：

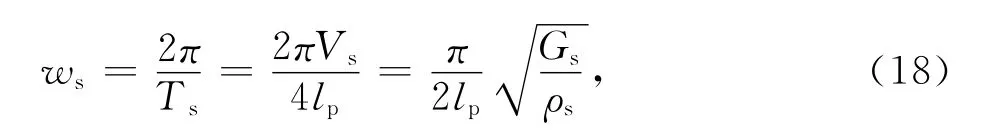
由式（16）～（18）可得到两者的频率比：

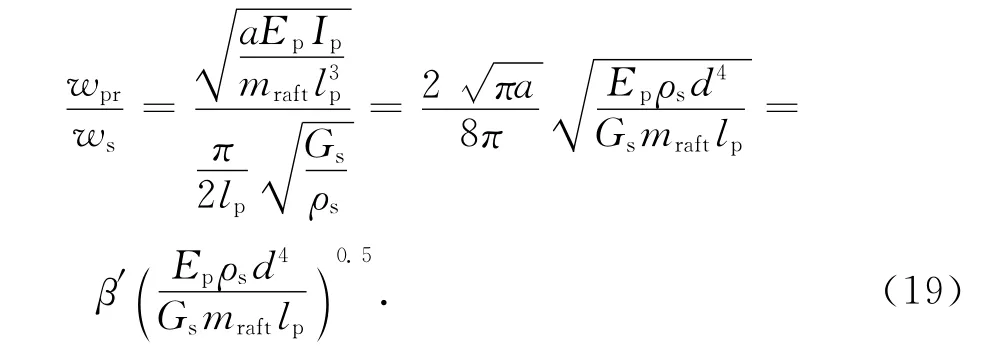
5）等效地基域的质量与基础质量（包括上部结构传至基础的荷载）之比：

此项主要表达地基域与基础体系的惯性质量之比，即表达地基域与基础体系的惯性强弱表征.假设桩在土体的延伸深度决定着其所影响的地基域范围，即桩在土体内的延伸越长，其所影响的地基域范围也越广，因此：

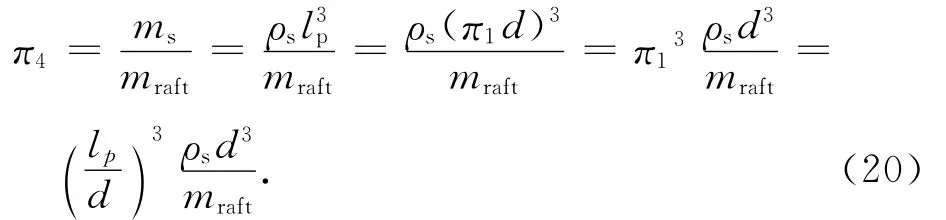
6）地震峰值加速：

其中，g为重力加速度.

3 π式的优化组合

根据量纲分析原理，各π式可表示成幂积关系［16］.因此，无量纲弯矩π0可由其他5个无量纲π式表达如下：

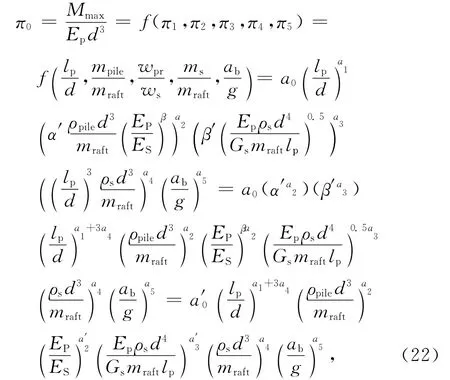
式中，a′0、a1～a5、ab为常数.

对于地震条件下的软黏土，渗透系数较小，且因地震时间较短，不易排水，故：

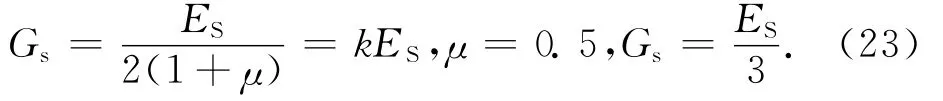
将式（13）代入式（12），得：

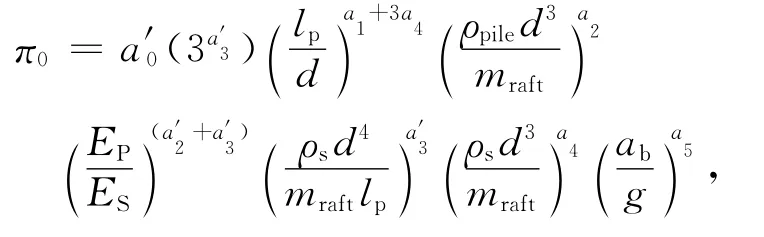
即：

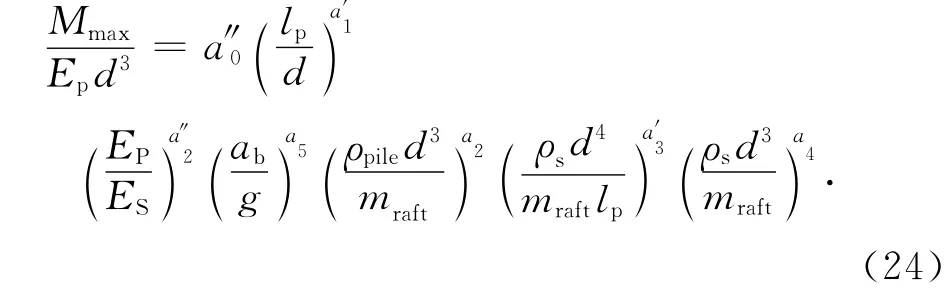
将表1中所有弯矩数据绘于图1中，可见：极其分散且毫无规律.逐次引入上述推导所得“π式幂”（如先引入π0，见图2），并不断动态试探和误差控制可将这些原始数据点压缩至一个最小范围的线性窄带中（见图3），经数学分析可确定式（24）中待定参数a″0，a′1，a2，a″2，a′3，a4和a5的最佳值，见式（25）、（26）.

图1 各种工况下桩基的原始最大弯矩值Fig.1 Original maximum bending moment of pile with different slender ratio under different cases

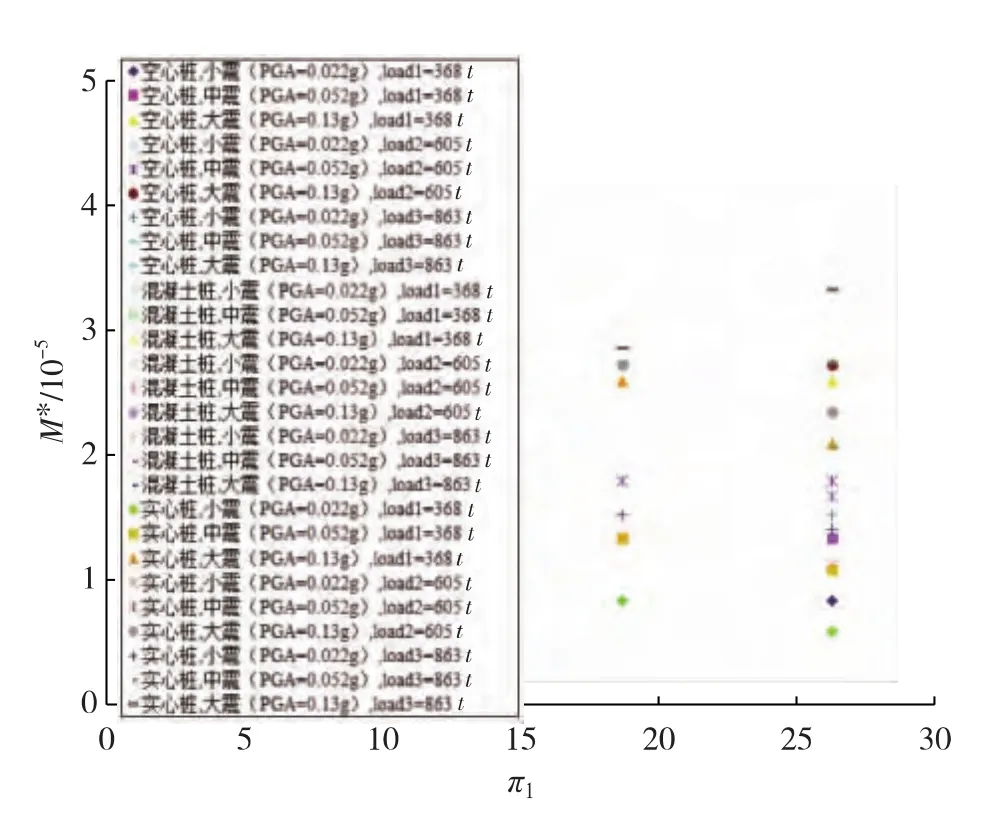
图2 π0与桩基长细比π1的关系Fig.2 Relation betweenπ0and slender ratio

图3可得，数据群“窄带”线性方程：Y＊＝0.147 X＊，Y＊与X＊分别代表引入π式幂变量后的复合指标，因此：通过还原各π式幂，即：

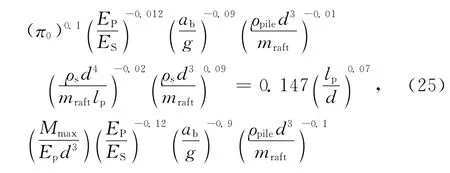
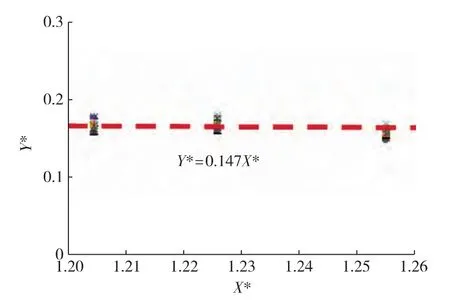
图3 最终压缩得到的线性窄带Fig.3 Final condensed plot after a series of linearization

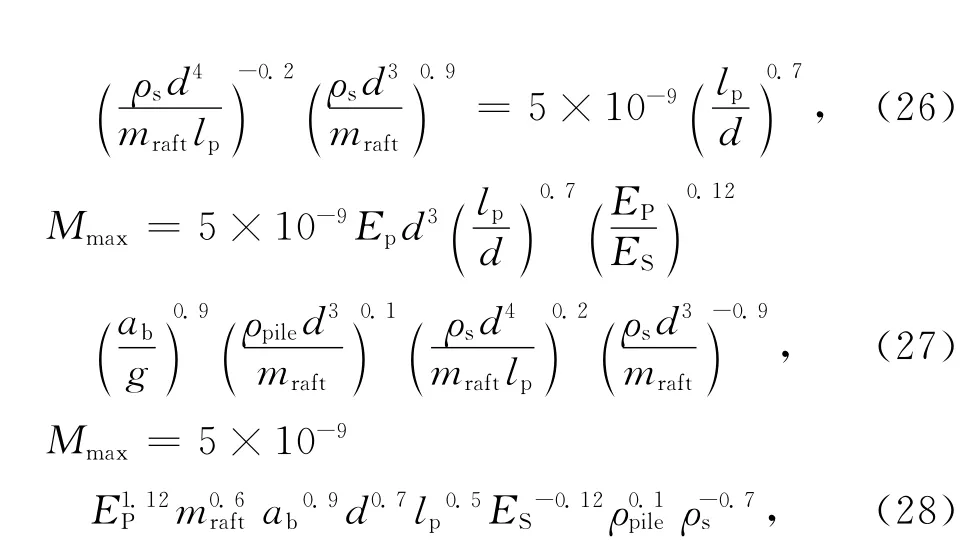
由于本研究中（试验及ABAQUS计算分析）上部结构传至筏板荷载由4根桩共同承担，故有：

mload为每根桩基单独承担的荷载，因此式（28）可进一步改写为一般形式：

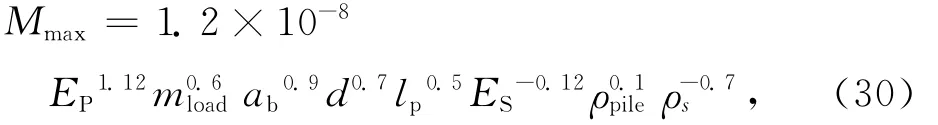
式（30）导出了多因素下桩基最大弯矩的最终计算公式，它考虑了包括上部结构传至桩基荷载水平在内的最广泛影响因素.该式是基于试验和ABAQUS计算数据导得［17－18］.通过对式中各参数的逐一敏性分析，可知其符合既往研究和工程实际的因素变化趋势（如：Mmax∝E1.12P最大弯矩随桩基刚度而增大，桩基刚度越大，产生的弯矩也越大；Mmax∝a0.9b最大弯矩随地震强度增大而增大等）.

4 预测公式与权威设计图表对比

Tabesh和Poulos［19］基于 Winkler地基梁的理论分析和数值计算，提出了在地震作用下桩身最大弯矩的几类工程设计图表.该研究假设线弹性均质土体中单桩受到从基岩输出的地震波作用，峰值加速度（PGA）均为0.1 g；桩基包括木桩和混凝土桩两类型，弹性模量分别设为10和30GPa；桩径范围为0.2～1.5m；土的弹性模量包括25，50和100MPa 3种；桩头承受的荷载采用极限承载力安全系数来表达，分别为2，2.5和3.

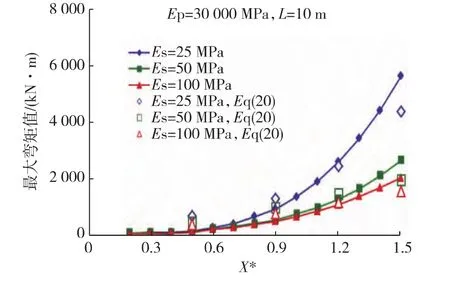
图4 式（30）确定的最大弯矩值与 Tabesh［19］对比Fig.4 Comparison of maximum bending moments between Eq（30）of this study and the design charts by Tabesh［19］

图4为本文式（30）与 Tabesh［19］计算得出的桩身最大弯矩对比，可见，在桩径较小情况下，两者计算的桩基最大弯矩基本相符，在桩径较大时差异较大.因式（30）和在 Tabesh和Poulos［19］的研究思路与方法完全不同，但总体上言，量值和变化趋势两者基本一致，说明本文导出的式（30）是合理正确的，在目前尚无成熟的桩基抗震规范情况下是具有一定参考价值的.

5 总 结

本文运用π定理，在既往研究获取的大量原始桩基弯矩的基础之上，通过充分考虑影响桩基弯矩的诸多因素，提出并推导出6个无量纲π式，通过数学分析为桩基（桩筏固定联接）在地震作用下产生的最大附加弯矩理论推导得出的计算公式，符合权威工程设计图表规律，具有一定工程应用性.本文所讨论的是黏性土中桩基，对于砂性土，其地震破坏模式主要是液化及其导致的大变形，这在国内外有较多研究成果可以借鉴；对于多层土中桩基弯矩计算，可按最不利土层参数或各层土参数的加权平均取值.

本文为桩基抗震研究提供了一种新的研究思路，当原始研究数据足够多（试验及数值计算）时，导出的计算弯矩公式更为准确，并力求在工程设计实践中得到检验、修正并积累经验.

［1］贺斌.地震作用下海洋环境码头桩－土动力相互作用分析［D］.武汉：武汉大学，2004.

［2］孔德森.桩－土相互作用计算模型及其在桩基结构抗震分析中的应用［D］.大连：大连理工大学，2004.

［3］戚玉亮.地基土－群桩－悬索大桥体系抗震动力相互作用数值模拟与理论研究［D］.上海：同济大学，2010.

［4］史佩栋，顾晓鲁.桩基工程手册［M］.北京：人民交通出版社，2008：177－214.

［5］史佩栋，高大钊，桂业琨.高层建筑基础工程手册［M］.北京：中国建筑工业出版社，2000：233－267.

［6］马亢，裴建良.桩筏基础－土动力相互作用的离心机模型试验 研 究 ［J］.岩 石 力学与 工 程 学 报，2011，30（7）：1488－1495.

［7］马亢，裴建良.桩－土动力相互作用问题中桩身刚度的影响效应研究［J］.岩石力学与工程学报，2011，30（增刊2）：3626－3632.

［8］马亢，许强.桩－筏－土体系的地震软化效应及ABAQUS模拟研究［J］.岩石力学与工程学报，2012，31（增刊1）：3254－3354.

［9］禹华谦.工程流体力学［M］.西安：西安交通大学出版社，1999：122－156.

［10］Fin W D.A study of piles during earthquakes：issues of design andanalysis［J］.Bulletin of Earthquake Engineering，2005，3（2）：141－234.

［11］Yu Y，Lee F H.Seismic response of soft ground［J］.Physical Modeling in Geotechnics：ICMG，2002，2：519－524.

［12］Nikolaou A S，Mylonakis G，Gazetas G.Kinematic ben－ding moments in seismically stressed piles［R］.National Center for Earthquake Engineering Research.Buffalo：State University of New York，1995：122－157.

［13］Nikolaou S，Mylonakis G，Gazetas G.Kinematic pile bending during earthquakes：analysis and field measurements［J］.Geotechnique，2001，51（5）：425－440.

［14］Poulos H G，Davis E H.Pile foundation analysis and design［M］.［S.l.］：John Wiley＆ Sons，1980：198－234.

［15］Randolph M F.The response of flexible piles to lateral loading［J］.Geotechnique，1981，31（2）：247－259.

［16］Andrew C.Dimensional analysis and intelligent experimentation［M］.Singapore：World Scientific Publishing Co Ptc Ltd，2008：342－367.

［17］Ma K，Banerjee S，Lee F H，et al.Dynamic soil－pile－raft interaction in normally consolidated soft clay during earthquakes［J］.Journal of Earthquake and Tsunami.2012，6（3）：1250031.

［18］Ma K，XU Q.Seismic softening behavior of pile－raft foundation constructed in clayey soil site subjected to far field earthquake［J］.Journal of Vibroengineering.2014，16（2）：626－642.

［19］Tabesh A，Poulos H G.Design charts for seismic analysis of single piles in clay［J］.Proceedings of the Institution of Civil Engineers Geotechnical Engineering，2007，160（2）：85－96.