基于单像素相机重构矩阵优化的影像采集和重构方法
2014-12-01刘玉安
程 涛,刘玉安
(1.广西科技大学汽车与交通学院,广西 柳州 545006;2.武汉大学测绘遥感信息工程国家重点实验室,湖北 武汉 430079)
0 引言
压缩感知理论表明,如果信号是稀疏的就能以远低于奈奎斯特(Nyquist)采样频率的采样率采集信号,并能以高概率精确重建信号。但是,影像等信号一般都不是稀疏的,而是可压缩的。因此,需要对影像等可压缩信号作稀疏变换以适应压缩感知的要求。可压缩信号的压缩感知模型如式(1)所示。

式(1)中:y是测量数据,y∈RM;Φ 是测量矩阵,Φ∈RM×N;Ψ 是稀疏变换基,Ψ ∈RN×N;x是可压缩信号,x∈RN,x=ΨTα;α为x的稀疏变换域系数,α∈RN,α=Ψx;重构矩阵ΠR=ΦΨT。
压缩感知的数据采集处理过程可分为测量和重构两个阶段。在测量阶段通过测量矩阵Φ以y=Φx采集测量数据y;在重构阶段,求解式(1)得到变换域系数,并通过=取得重构信号。
对于可压缩信号,如果测量矩阵和稀疏变换基的不相关性好,那么重构矩阵的信号重构能力就强[2]。在大家寻找与稀疏变换基不相关性好的测量矩阵时,Elad[3]却提出了截然不同的测量矩阵设计思路。Elad[3]和Duarte[4]等在稀疏变换基已确定的情况下,以重构矩阵各列相关性最小化或平均化为目标优化重构矩阵;然后,通过稀疏变换基和优化后的重构矩阵(简称优化矩阵)解算出与之相应的测量矩阵。尽管优化矩阵有更好的重构能力,但是测量矩阵不再是原测量矩阵。即使原测量矩阵是便于电路设计的确定性矩阵或便于硬件实现的单像素相机采用的0-1随机矩阵,测量矩阵也不会再保持原测量矩阵的优良性质。Elad等人的重构矩阵优化算法尽管能够事前确定稀疏变换基,却无法事前确定测量矩阵,也就无法改变当前测量矩阵难以硬件实现和设计的窘境,因而应用价值有限。
稀疏信号无需作稀疏变换,所以这时测量矩阵就是重构矩阵。文献[2,5—6]通过测量矩阵的行向量正交化以及列向量单位化来优化测量矩阵。优化后的测量矩阵尽管能改善信号重构效果,但是和Elad的方法一样,优化后的测量矩阵性质存在不确定性和未知性,也存在难以硬件实现的问题,不适合工业化应用。
文献[1]针对稀疏信号提出了测量矩阵和测量数据的事后优化算法和模型。实现了在测量阶段采用事前确定的测量矩阵(0-1稀疏矩阵)采集测量数据,在重构阶段采用优化后的测量矩阵(高斯矩阵)重构稀疏信号,取得了很好的效果,并给出了相关的理论分析和证明。
如能将文献[1]的测量矩阵分离算法推广应用于可压缩信号,就可克服Elad等人重构矩阵优化算法的缺点。在稀疏变换基确定的情况下,实现以事前确定的测量矩阵采集数据,以事后优化的重构矩阵重构信号。从而初步解决当前测量矩阵难以硬件实现和设计的难题,并且保持高的信号重构能力。
离 散 余 弦 变 换 (Discrete cosine transform,DCT)编码是影像/视频压缩采用的主流技术[7]。单像素相机的0-1随机矩阵不但易于硬件实现而且所需存储空间小运算速度快。因此,以离散余弦变换矩阵作为式(1)的稀疏变换基,以单像素相机的0-1随机矩阵作为式(1)的测量矩阵。为便于与同行研究成果作对比和硬件设计,测量矩阵的大小为128×256,各行向量包含32个随机均匀分布的1。
尽管单像素相机测量矩阵(0-1随机矩阵)和稀疏变换基(DCT矩阵)的不相关性很差,但是理论和实验证明,基于单像素相机重构矩阵优化的方法依然能取得好的信号重构效果。从而回避了Donoho等人[2]提出的“测量矩阵和稀疏变换基不相关性好”的测量矩阵设计原则。本文针对压缩感知在遥感中的真实应用情境,提出了无需把二维影像转化成一维信号的基于线阵推扫和重构矩阵优化的单像素相机影像采集和重构方法。
1 重构矩阵的优化算法和近似矩阵的计算公式
文献[1]的测量矩阵优化算法,只适用于稀疏信号,可使优化后的测量矩阵具备行模相近、列模相近、各行不相关性好和各列不相关性好以及服从高斯分布5个特征。影像等可压缩信号作稀疏变换后,可近似视为稀疏信号。因此,在文献[1]的测量矩阵优化算法中引入稀疏变换基,即可变成适用于可压缩信号的重构矩阵优化方法,如算法1所示。
算法1:
输入:测量矩阵Φ和稀疏变换基Ψ初始化:ΠR=Φ ΨT,设定迭代次数i的初始值为0,最大值imax默认为100迭代:在第i次迭代执行以下步骤
1)以Jarque-Bera检验计算ΠR各列和各行服从高斯分布的行数Jri和列数Jci;
2)计算ΠR各列向量间的相关系数,取出其绝对值的最大值μcimax;计算各行向量间的相关系数,取出其绝对值的最大值μrimax;
3)计算ΠR各行向量的模,取出其最大值normrimax和最小值 normri min;
4)正交规范化ΠR各行向量,单位化ΠR各列向量;
5)使i=i+1,判断i<imax,如果是退出迭代,否则返回执行步骤1;
输出:优化后的重构矩阵ΠO。
因为算法1也是以行变换为主的算法,所以只要在文献[1]的近似矩阵计算公式中引入稀疏变换基,把测量矩阵换成针对可压缩信号的重构矩阵就可得到重构矩阵的近似矩阵计算公式,如式(2)所示。
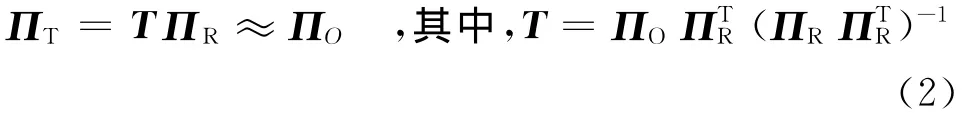
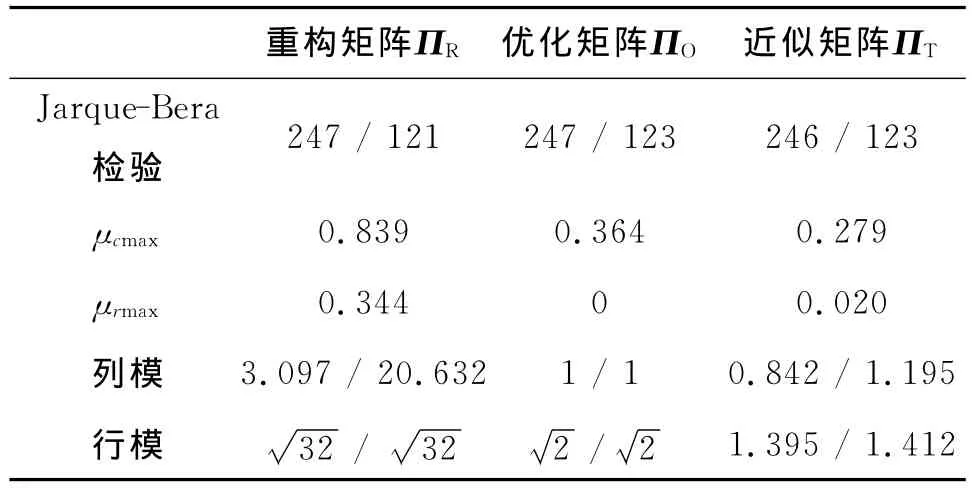
表1 3类矩阵的相关参数Tab.1 Parameters of 3matrices
表1列出了测量矩阵采用单像素相机的0-1随机矩阵,稀疏变换基采用DCT矩阵的算法1迭代100步时重构矩阵ΠR、优化矩阵ΠO和近似矩阵ΠT的各种统计学参数(表1中各行数据,除“Jarque-Bera检验”外,“/”号左边的数据表示最小值,“/”号右边的数据表示最大值;“Jarque-Bera检验”行,“/”号左边的数据表示符合检验的列数;“/”号右边的数据表示符合检验的行数)。μcmax表示列间相关系数绝对值的最大值;μrmax表示行间相关系数绝对值的最大值。因为采用的测量矩阵是各行都包含32个1的0-1随机矩阵,而且DCT矩阵是正交矩阵,所以重构矩阵的行模都为
2 重构矩阵优化算法的迭代过程分析
根据文献[1]的理论和实验分析,只要优化矩阵和近似矩阵同时具备行模相近、列模相近、各行不相关性好和各列不相关性好就会对高斯稀疏信号具有很好的重构能力,如果优化矩阵和近似矩阵各行和各列几乎都满足高斯分布就会同时具备高斯矩阵对各类稀疏信号的普适性。因此本文以此为判据分析图1—图4所表示的算法1对重构矩阵的迭代优化过程和相应的近似矩阵的性质变化。图1和图4中,由于迭代0处的y值过大,故只能部分显示,0处的y值可由表1查得。
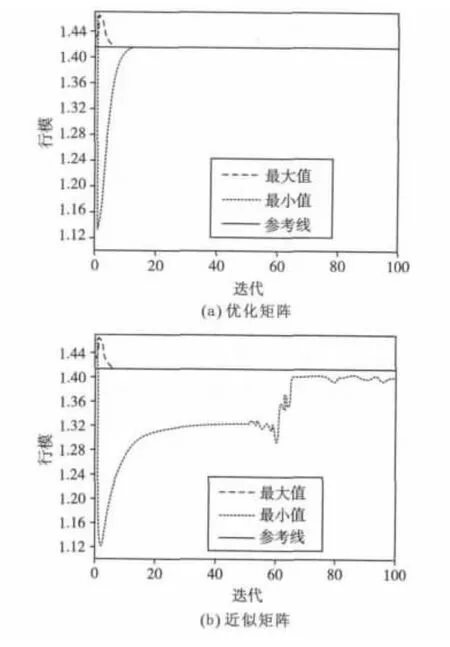
图1 矩阵各行模的极值与迭代数的关系Fig.1 Row norms extreme value of matrix vs.iteration
由图2(a)可见优化矩阵的各行列相关系数绝对值的最大值在迭代过程中迅速收敛,在第13次迭代后数值不再变化,曲线变成直线。由表1可见,优化矩阵的行相关系数为0,即各行完全正交;优化矩阵的列相关系数也由0.839减小到0.364。由图2(b)可见近似矩阵的各列相关系数绝对值的最大值在迭代过程中也迅速变小收敛,行相关系数最大值到第70次迭代后才基本稳定。由表1可见,近似矩阵的行相关系数为0.02,各行几乎完全正交;近似矩阵的列相关系数也由0.839减小到0.279。
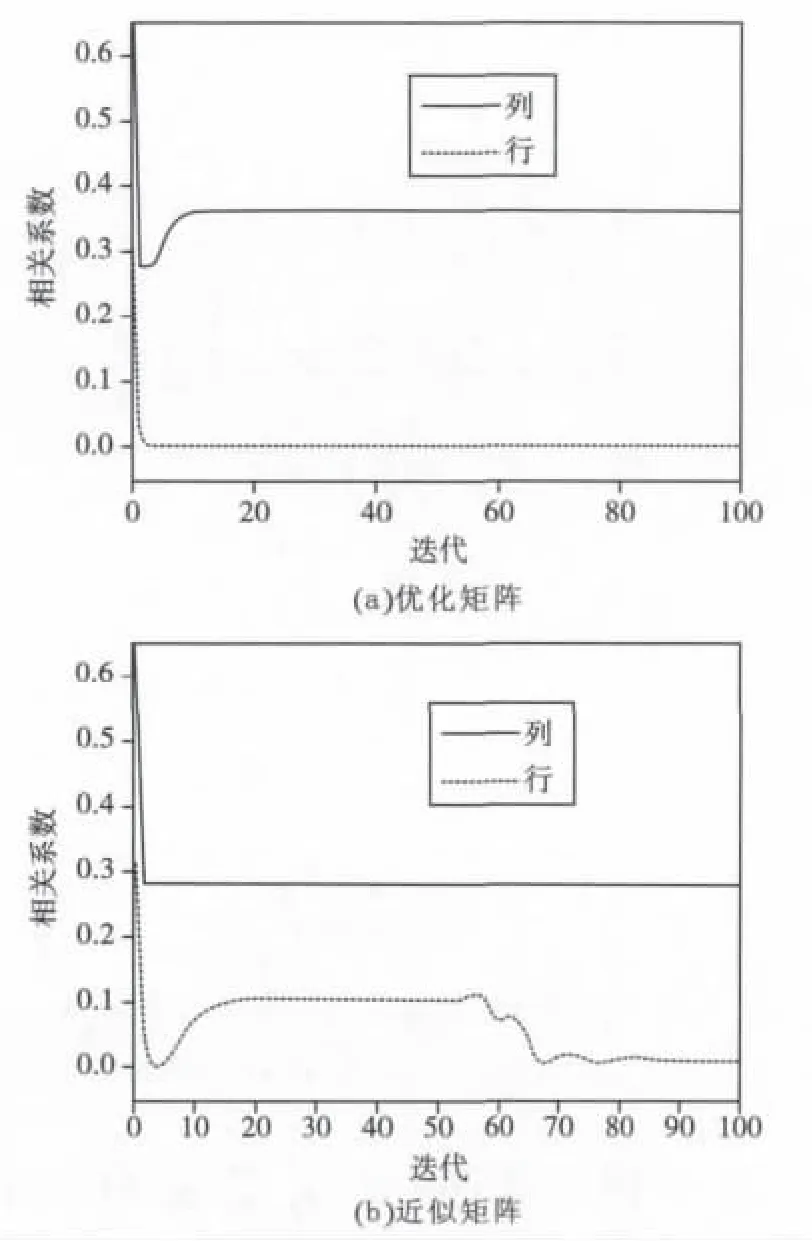
图2 矩阵各行列相关系数绝对值的最大值与迭代的关系Fig.2 Maximum of absolute value of correlation coefficient of matrix rows and columns vs.iteration
由图3(a)可见优化矩阵的各行列在第60次迭代后基本都服从高斯分布(第100次迭代后各行列服从高斯分布的数量各为247和123,如表1所示),说明重构矩阵已演变为高斯矩阵。图3(b)和(a)的曲线构型非常相似,也是在第60次迭代后各行列基本都服从高斯分布(第100次迭代后各行列服从高斯分布的数量各为246和123,如表1所示)。由图4可见近似矩阵的列模极值收敛到与1很接近的值。由于算法1每次迭代的最后一步都是“单位化ΠR各列向量”,所以优化矩阵各列模的值都为1,如表1所示。
由表1和图1-图4可见,优化矩阵具备各行不相关、各列不相关性好、各行模相等和各列模相等4个优点,而且优化矩阵各行和各列几乎都服从高斯分布。基于算法1和式(2)的近似矩阵很好地继承了优化矩阵的性质。因此,文献[1]的测量矩阵分离算法可推广应用于适用于可压缩信号的重构矩阵。
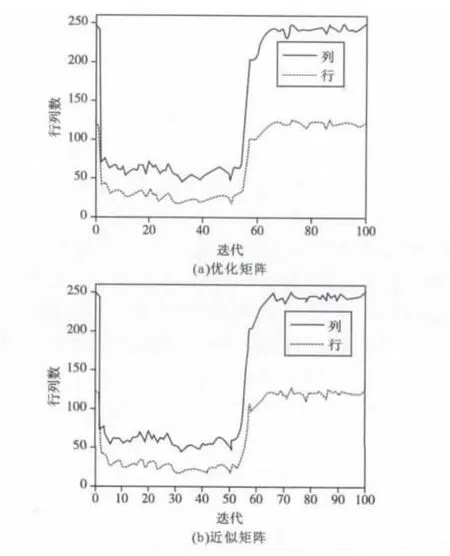
图3 矩阵服从高斯分布行列数与迭代的关系Fig.3 Number of rows and columns which follows the gauss distribution vs.iteration
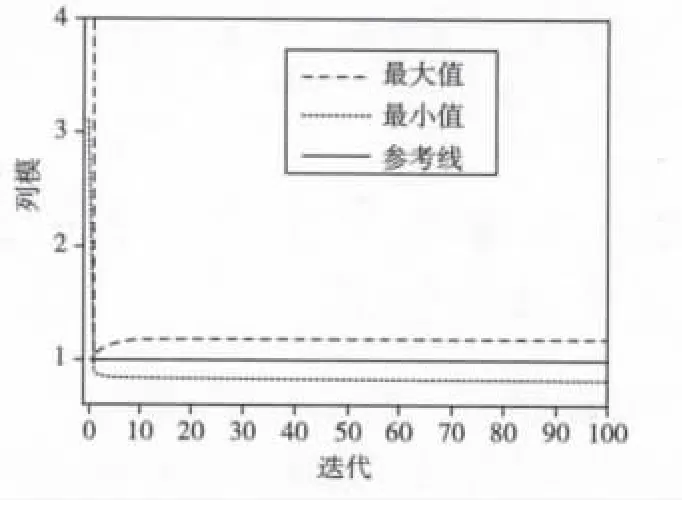
图4 近似矩阵各列模极值与迭代数的关系Fig.4 coumn norm extreme value of approximate matrix vs.iteration
3 重构矩阵优化算法的理论分析
进一步通过Kolmogorov-Smirnov检验可以发现,优化矩阵不仅服从高斯分布,而且服从N(0,1/M)分布。因此,优化矩阵各行模的平方服从χ2分布,即各行模的数学期望为。由图1(a)可见,第16次迭代后,行模极值都收敛于,与其数学期望值相同。
尽管测量矩阵是各行都包含32个随机均匀分布的1的0-1随机矩阵,但依然可视为各元素满足独立同分布性质。由表1可见,由测量矩阵和DCT矩阵(稀疏变换基)乘积所得的重构矩阵,通过Jarque-Bera检验服从高斯分布的行列数分别为121和247。因此,重构矩阵可视为高斯矩阵。
算法1中行正交化操作尽管涉及多个行的运算,根据线性变换不变性原理可知正交化后的各行和各列依然符合高斯分布。根据大数定律可知,在多次迭代过程中,各行和各列的高斯分布越来越接近于样本均值为0和样本方差为1/M的理想状态,服从N(0,1/M)分布的行列数分别为120和243。因此,优化矩阵各元素可视为来自服从标准高斯分布的样本总体。近似矩阵与优化矩阵的性质相近,近似矩阵各元素也可视为来自服从标准高斯分布的样本总体,服从N(0,1/M)分布的行列数分别为121和245。
对于不同的重构矩阵,算法1中迭代次数最大值的选取要满足如下条件:能够使图1、图2和图4中优化矩阵和近似矩阵的曲线随迭代收敛稳定,满足行模相近、列模相近、各行不相关性好和各列不相关性好4个优点;能够使图3中优化矩阵和近似矩阵服从高斯分布的行列数大于矩阵行列数的95%(即使随机生成的高斯矩阵也无法保证95%的行列数服从高斯分布)。
4 基于稀疏信号重构实验的重构矩阵优化算法的验证
尽管ΠR和ΠT是适用于可压缩信号的包含稀疏变换基的矩阵,但为了验证算法1和式(2)的有效性,分别以重构矩阵ΠR、优化矩阵ΠO和重构矩阵ΠT直接测量并重构高斯稀疏信号和0-1稀疏信号,检验3类矩阵的性能,实验结果如图5所示(采用Matlab在普通台式机上做仿真实验,CPU主频2 GHz,内存1GB)。图5以正交匹配追踪算法(orthogonal matching pursuit,OMP)对每个稀疏度K值重复试验500次,然后计算稀疏信号的精确重构概率。为更清晰地表达实验结果,图5只表示各曲线重构概率为1的最后一个点和重构概率为0的第一个点,以及两点之间的曲线部分。
由图5可见,优化矩阵和近似矩阵的重构效果远远好于重构矩阵,整条曲线都位于重构矩阵的右侧。优化矩阵和近似矩阵的重构效果基本一致,两条曲线几乎重合。说明算法1和式(2)都是非常有效可行的。因为0-1随机矩阵行列不相关性差[8-9],DCT矩阵也不是高斯矩阵,所以两者构成的重构矩阵的行列不相关性不好(如表1所示),由图5可见重构矩阵的重构效果极差。

图5 类矩阵的重构概率与稀疏度的关系Fig.5 Prob.of exact recovery vs.the sparsity by 3matrices
5 基于重构矩阵优化算法的单像素相机影像采集重构方法的验证
基于算法1和式(2)的近似矩阵计算方法可使近似矩阵很好地继承优化矩阵的性质。因此,能以过渡矩阵Τ实现重构矩阵ΠR和测量数据y的事后优化。在测量阶段采用易于硬件实现的0-1随机矩阵,以y=Φx采集数据;在重构阶段以过渡矩阵Τ将测量数据y和重构矩阵ΠR完善优化:yT=Τy,ΠT=ΤΠR,并以式(3)重构可压缩信号x的稀疏变换域系数α。最后,通过就能得到重构的可压缩信号
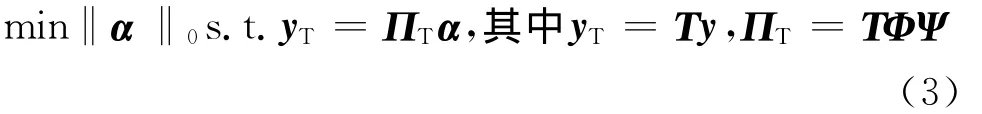
文献[10]等的压缩感知影像处理多是从原始影像中抽取16×16的子块,然后逐列首尾相接成向量。由于子块包含区域有限,均匀性好,因此能获得较好的影像重构效果。但是这样的方法并不利于影像的采集和测量矩阵的设计。在遥感等海量数据采集环境中多是采用线阵推扫数据采集方法。单像素相机采用的最小全变分法(Total Variation,TV)计算复杂度大,难以应用于海量数据处理环境。因此影像重构实验采用OMP算法。
图5只是验证了理想情况下重构矩阵、优化矩阵和近似矩阵的性能。为进一步验证真实情况下算法1、式(2)和式(3)的可用性和有效性,本文采用Lena图逐列作线阵推扫式影像采集和重构实验[11]。
近似矩阵、重构矩阵和优化矩阵的影像采集和重构过程如下。
近似矩阵ΠT:首先,以测量矩阵Φ(0-1随机矩阵)通过y=Φx对Lena图逐列扫描采集;其次,对测量数据y和重构矩阵ΠR事后优化:yT=Τy,ΠT=ΤΠR;然后,以OMP算法逐列求解min‖α‖0s.t.yT=ΠTα,得到;最后,解算=即可得到Lena图的重构影像。
重构矩阵ΠR:首先,以测量矩阵Φ(0-1随机矩阵)通过y=Φx对Lena图逐列扫描采集;然后,以OMP算法逐列求解min‖α‖0s.t.y=ΠRα,得到;最后,解算=。
优化矩阵ΠO:首先,对影像逐列作稀疏变换α=Ψx,取得α;其次,通过y=ΠOα逐列取得Lena图的测量数据y;然后,以OMP算法逐列求解min‖α‖0s.t.y = ΠOα,得到;最后,解算=(优化矩阵ΠO无法应用于真实的影像采集作业,只是为了与重构矩阵和近似矩阵作影像重构能力的对比分析,而虚拟了优化矩阵的影像采集)。
3类矩阵(重构矩阵、优化矩阵和近似矩阵)的重构效果如图6所示(从上到下分别是Lena、Boats和意大利撒丁岛Mulargia湖图;从左至右分别是重构矩阵、优化矩阵和近似矩阵的重构影像,最右边的是原始影像)。Mulargia湖的遥感影像由Landsat-5卫星在波段4拍摄于1996年7月。表2是3类矩阵重构图的信噪比(Signal to Noise Ratio,SNR)和峰值信噪比(Peak Signal to Noise Ratio,PSNR)。
由表2可见,重构矩阵的SNR和PSNR最小;优化矩阵的SNR和PSNR比重构矩阵分别约提高0.5~1.5dB;近似矩阵的SNR和PSNR与优化矩阵基本相当,变化不大。这进一步说明算法1、式(2)和式(3)都是有效可行的。OMP算法并非是一个高效的算法,但是它是其他各类匹配追踪算法的基础,如采用其他匹配追踪算法有可能进一步改善影像的重构效果。因此,工业化应用中可以采用基于近似矩阵和线阵推扫模式的单像素相机影像采集和重构方案。

表2 3类矩阵重构Lena、Boats和Mulargia湖图的信噪比和峰值信噪比Tab.2 SNR and PSNR of reconstructed Lena、Boats and Mulargia lake of 3matrices

图6 3类矩阵的重构效果图Fig.6 Reconstruction effect drawing of 3matrices
6 结论
在稀疏变换基(DCT矩阵)和单像素相机测量矩阵(0-1随机矩阵)已确定的情况下,本文提出了以事前确定的测量矩阵(0-1随机矩阵)采集数据,以事后优化的重构矩阵(近似矩阵)重构信号的方法。既初步解决了当前测量矩阵难以硬件实现和设计的难题,又改善提高了信号的重构效果。同时回避了“测量矩阵和稀疏变换基不相关性好”的测量矩阵设计原则。实验和理论分析表明无需把二维影像转化成一维信号的基于线阵推扫和重构矩阵优化的单像素相机影像采集和重构方法是可行的。拟将本文的测量矩阵转变为0-1稀疏循环矩阵作进一步的深入研究。
[1]程涛,朱国宾,刘玉安.基于0-1稀疏循环矩阵的测量矩阵分离研究 [J].光学学报,2013,33(2):1-6.
[2]DONOHO D L.Compressed sensing [J].Information Theory,IEEE Transactions on,2006,52(4):289-306.
[3]ELAD M.Optimized Projections for Compressed Sensing[J].Signal Processing,IEEE Transactions on,2007,55(12):695-702.
[4]DUARTE-CARVAJALINO J M,SAPIRO G.Learning to Sense Sparse Signals:Simultaneous Sensing Matrix and Sparsifying Dictionary Optimization[J].Image Processing,IEEE Transactions on,2009,18(7):395-408.
[5]DONOHO D L,TSAIG Y,DRORI I,et al.Sparse Solution of Underdetermined Systems of Linear Equations by Stagewise Orthogonal Matching Pursuit[J].Information Theory,IEEE Transactions on,2012,58(2):94-121.
[6]CANDES E J,TAO T.Near-Optimal Signal Recovery From Random Projections:Universal Encoding Strategies[J].Information Theory,IEEE Transactions on,2006,52(12):6-25.
[7]潘榕,刘昱,侯正信,等.基于局部DCT系数的图像压缩感知编码与重构 [J].自动化学报,2011,37(6):74-81.
[8]DUARTE M F,DAVENPORT M A,TAKHAR D,et al.Single-Pixel Imaging via Compressive Sampling [J].Signal Processing Magazine,IEEE,2008,25(2):83-91.
[9]AKCAKAYA M,JINSOO P,TAROKH V.A Coding Theory Approach to Noisy Compressive Sensing Using Low Density Frames [J].Signal Processing,IEEE Transactions on,2011,59(11):69-79.
[10]刘亚新,赵瑞珍,胡绍海,等.用于压缩感知信号重建的正则化自适应匹配追踪算法 [J].电子与信息学报,2010,32(11):3-7.
[11]程涛,朱国宾,刘玉安.基于二维压缩感知的定向遥感和变化检测研究 [J].红外与毫米波学报,2013,32(5):1-6.
