基于Kriging插值无网格法的动力弹塑性分析

熊勇刚 ，田万鹏，陈科良，陈云飞 ，杜民献，吴吉平

(1. 湖南工业大学 机械工程学院，湖南 株洲，412007；2. 东南大学 机械工程学院，江苏 南京，210000)

无网格方法近年来得到了较大发展，是目前科学和工程计算方法研究的热点之一[1−3]。与有限元法不同，无网格方法的近似函数是建立在一系列离散点上的，可以部分或彻底消除网格，从而有效地避免了由于网格的依赖性而带来的种种困难。目前，发展的无网格方法主要有无单元 Galerkin法[4−5]、无网格局部Petrov-Galerkin法[6]、光滑粒子流体动力学法[7−8]、再生核粒子法[9]、复变量无网格方法[10]、边界无单元法[11−12]、无网格流形方法[13]以及自然单元法[14]等，其中，无单元Galerkin法是发展良好和最具有应用价值的无网格方法之一[1]，但该法的最大缺点是采用移动最小二乘法构造的形函数不满足Kronecker delta函数性质，因此，本质边界条件的施加非常困难，需要采用特别技术进行处理。Kriging插值无网格法是在构造形函数时采用滑动 Kriging插值代替移动最小二乘法而发展起来的一种改进的无单元 Galerkin法。滑动Kriging插值法构造近似函数不仅数值实现简单、计算量小，而且满足Kronecker delta函数性质，从而可以非常方便地施加本质边界条件[15−16]。为此，本文作者将 Kriging插值无网格法应用于动力弹塑性问题的求解计算。首先详细推导 Kriging插值无网格法在动力弹塑性问题中的理论公式，然后，给出基于 Kriging插值无网格法的动力弹塑性分析的数值实现方法和具体算例。

1 滑动Kriging插值

与移动最小二乘法相似，假设任意计算点x的影响域内包含n个节点。滑动Kriging插值的逼近函数采用如下线性回归模型与偏差之和的模式：

式中：pT(x)为多项式基函数；a为待求常系数向量；z(x)为一个均值为0、方差为σ2、协方差不为0时的局部离差。对于二维情况，p(x)可选取如下二次基：

用式(1)对n个样本点进行插值，则z(x)的协方差可表示为

θ＞0，为模型参数；为给定2点xi和xj之间的相关距离。

计算点x与所给定的n个节点之间的相关函数向量为

在给定的n个节点处的函数值已知时，

式中：u为n个节点处场函数的集合。当采用线性回归模型式(1)表达u时，有

式中：Pm与Z分别为给定点上基函数值所形成的矩阵及线性逼近的误差向量，且有

对计算点x，采用已知节点的函数值对场函数u(x)进行线性逼近，有

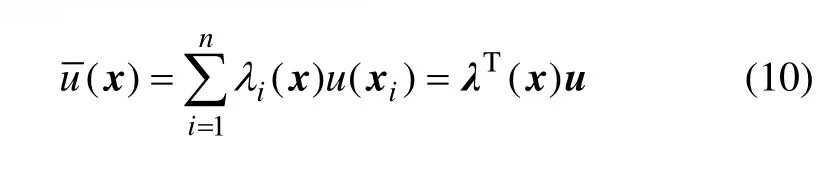
于是，式(1)与式(10)之间的误差函数为

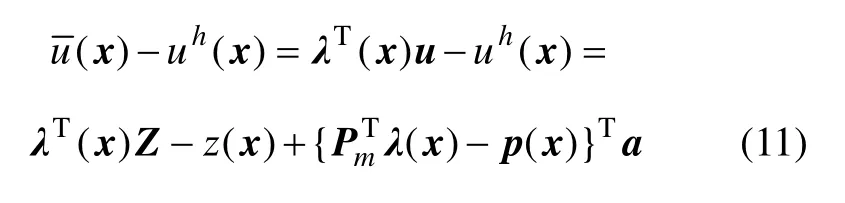
要保证无偏估计，必须满足如下约束条件：

式(11)中误差函数的均方差为

为了确定最优的线性估计，将式(13)作为目标函数，式(12)作为约束条件，进而根据Lagrange不定乘子法可以将其转化为无条件的极小值问题。通过对向量λT(x)求偏导数为0得到一组方程，求解此方程组可得到最优线性无偏估计条件下的插值函数[15−16]：

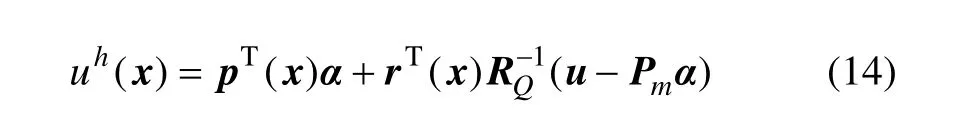
式中：

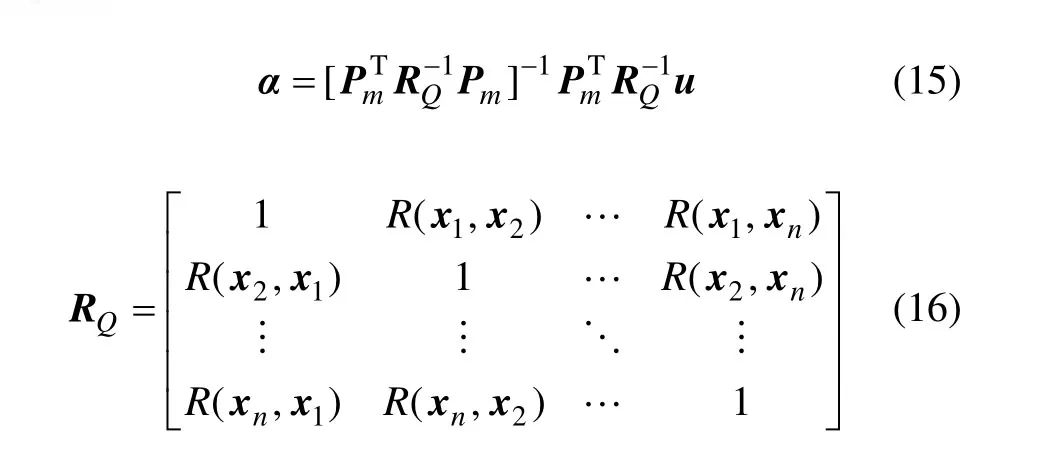
同时，为了便于表述，定义

式中：I为n×n阶单位矩阵。于是，式(14)可改写为

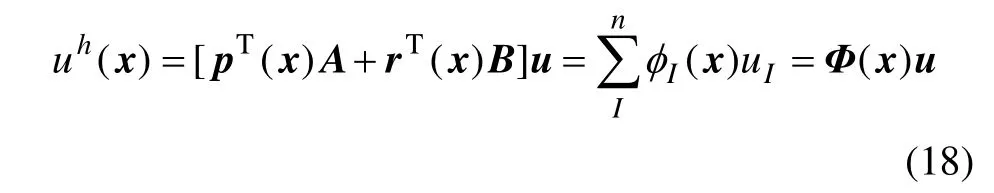
AjI为矩阵A的第j行、第I列元素；BkI为矩阵B的第k行、第I列元素。

形函数φI(x)关于x和y的导函数分别为

2 动力弹塑性分析的Kriging插值法

2.1 控制方程

考虑二维动力弹塑性问题，其计算域为Ω，边界为控制方程为：

式中：ρ为质量密度；为节点加速度，且有=∂2u/∂t2；ui为节点位移；t为时间；为应力；为应变；bi为体力；Γu和Γt分别为位移和面力已知的边界。采用von Mises屈服准则、关联流动准则和各向同性硬化准则时，式(22)中的弹塑性

其中：

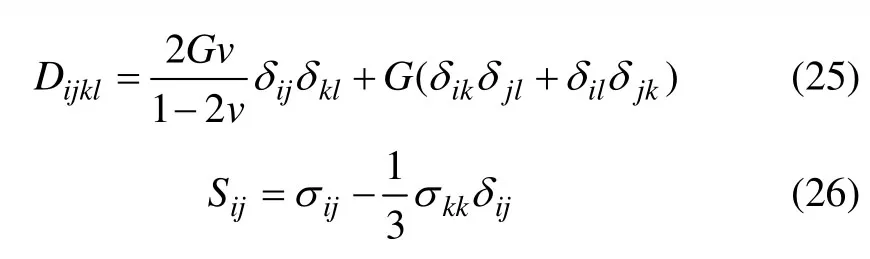
σeq和H分别为等效应力和塑性模量；G和v分别为剪切模量和泊松比。

应力和位移满足如下边界条件

和初始条件

式中：nj(x)为Γ上点x处的外法线方向余弦；和分别为已知的位移和面力分量；u0和v0分别为初始位移和初始速度。

2.2 空间离散

平衡方程式(21)的弱形式可以通过加权残值法获得，即

式中：wi为权函数。对式(29)进行分部积分，并考虑到自然边界条件式(27)，有

由于只对空间域进行离散，求解域Ω内的试函数可以由式(18)表示为

将空间离散后的位移表达式(31)代入式(30)，且令权函数等于形函数，最终可得弹性动力学的离散方程为

式中：M，K和f(t)分别为质量矩阵、刚度矩阵与载荷向量；

对于动力弹塑性问题，式(32)可以改写为

节点内力向量P(σ(t))为

其中：σ(t)为应力向量。

2.3 求解方案

本文采用传统的 Newmark方法对时间域进行离散。Newmark法于1959年由线性加速度法延伸推导而得，是一种应用相当广泛的直接积分法。由于塑性变形的非线性特性，在每个时间步都必须进行迭代计算。在t和t+Δt时间步内的迭代求解过程如下[17−19]：

(1) 令迭代计算变量k=0；

(2) 在开始预估阶段，令

(3) 利用下述方程计算残余力：

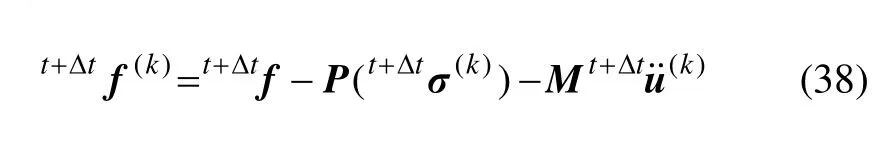
(4) 如有需要，应用下式形成等效刚度矩阵：

否则，就应用前面已计算的K*。

(5) 求解方程：

(6) 进入修正阶段，令

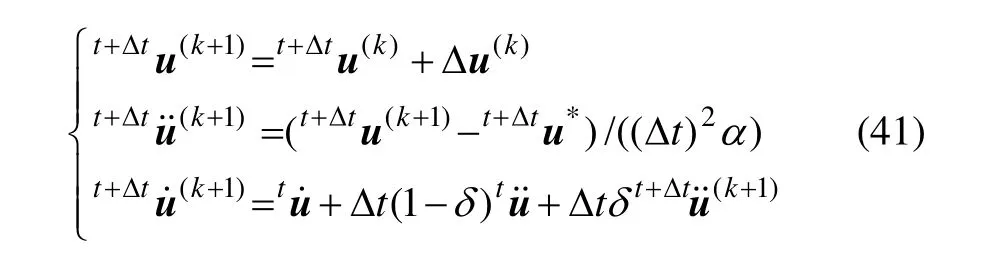
式中：α和δ是按积分精度和稳定性要求决定的参数。当δ≥0.5和α≥0.25(0.5+δ)2时算法是无条件稳定的，即时间步长Δt不影响解的稳定性。

(7) 迭代收敛检查。对于给定的收敛误差εR，若||Δu(k)||≤εR，则结束本时间步内的迭代循环，否则，令k=k+1并转到第3步。

(8) 为了使下一个时间步使用，令

给定初始位移u0和初始速度v0后，可以从下式求出初始加速度：

3 数值算例

为了验证以上提出的数值方法的有效性，本文分析2个算例。在滑动Kriging插值中，本文选用二次基函数，并且计算点x的影响域取为以点x为圆心的圆形域，半径dmax=scale×s[6](其中s[6]为计算点x到距其最近的第 6个节点之间的距离)，系数scale取为2.5。

算例1 受内压作用的厚壁圆筒。

1个内径a=1 m，外径b=2 m的厚壁圆筒，受到p=1.85×104Pa的突加内压作用，如图1所示。材料为理想弹塑性，并服从von Mises屈服准则。材料的弹性模量E=2.1×107Pa，泊松比ν=0.3，屈服应力σy=3.55×104Pa，质量密度ρ=7.85 kg/m3。该问题为平面应变状态下的1个经典算例。

图1 受内压作用的厚壁圆筒Fig. 1 A thick-walled cylinder subjected to internal pressure

由于对称性，可取结构的1/4作为计算模型。计算分析中采用图 1(a)所示的节点布置方案，且时间步长取为Δt=1.0×10−5s。图2所示为内表面的径向位移随时间的变化曲线。为了进行对比，图2还给出了有限元软件ABAQUS的计算结果。从图2可以看出：本文的计算结果与 ABAQUS的计算结果很吻合，说明本文推导的动力弹塑性分析的 Kriging插值无网格法及其离散形式是正确的，方法是可行的。

图2 内表面的径向位移Fig. 2 Radial displacement history at inner surface

算例2 受突加载荷的悬臂梁。

如图3所示为长L=1.2 m、高H=0.4 m的悬臂梁，在平面应力状态下端部受到突加剪切荷载p=2.5 kPa的作用。材料为理想弹塑性，并服从von Mises屈服准则。材料弹性模量E=2.1×107Pa，泊松比ν=0.3，屈服应力σy=4.0×104Pa，质量密度ρ=7.85 kg/m3。

在计算时，把区域均匀地划分为25×7个节点的网格，且时间步长取为Δt=1.0×10−4s。为了检验方法的有效性，本文使用有限元软件 ABAQUS的计算结果进行对比。图4所示为悬臂梁右端中点A的竖向位移随时间的变化曲线。从图4可以看出：本文的计算结果与 ABAQUS的计算结果很吻合，从而进一步验证了本文方法的有效性。

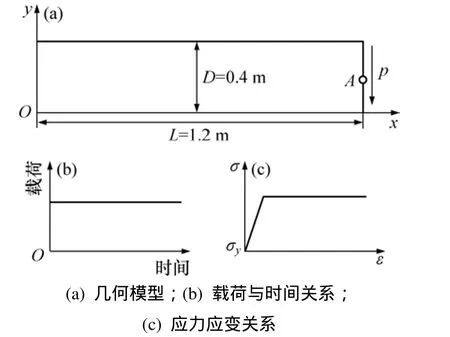
图3 受突加载荷的悬臂梁Fig. 3 Cantilever beam under Heaviside loading

图4 悬臂梁中A点的竖向位移Fig. 4 Vertical displacement of point A in beam

4 结论

(1) 采用Kriging插值无网格法，建立了进行结构弹塑性动力响应分析的一种新方法，推导了相应的计算公式，提出了具体的数值实现方法。数值计算结果表明，采用 Kriging插值无网格法进行动力弹塑性分析是可行的，它具有稳定性好和精度高等优点。

(2) 采用Kriging插值无网格法进行动力弹塑性分析只需要离散节点的信息，从而减少了前处理的工作量。尤为重要的是，滑动 Kriging插值法的形函数满足Kronecker delta函数性质，因而能够直接、准确地施加本质边界条件。此外，形函数导数的计算不涉及逆矩阵的求导，因而计算效率较高。

[1]Belytschko T, Krongauz Y, Organ D, et al. Meshless methods:An overview and recent developments[J]. Computer Methods in Applied Mechanics and Engineering, 1996, 139: 3−47.

[2]Li S F, Liu W K. Meshfree and particle methods and their applications[J]. Applied Mechanics Review, 2002, 55: 1−34.

[3]宋康祖, 陆明万, 张雄. 固体力学中的无网格方法[J]. 力学进展, 2000, 30(3): 55−65.SONG Kangzu, LU Mingwan, ZHANG Xiong. Meshless method for solid mechanics[J]. Advance in Mechanics, 2000,30(3): 55−65.

[4]Belytschko T, Lu Y Y, Gu L. Element-free Galerkin method[J].International Journal for Numerical Methods in Engineering,1994, 37: 229−256.

[5]王东东, 李凌, 张灿辉. 稳定节点积分伽辽金无网格法的应力计算方法研究[J]. 固体力学学报, 2009, 30(6): 586−591.WANG Dongdong, LI Ling, ZHANG Canhui. On stress evaluation in Galerkin meshfree methods with stabilized conforming nodal integration[J]. Chinese Journal of Solid Mechanics, 2009, 30(6): 586−591.

[6]Atluri S N, Zhu T L. A new meshless local Petrov-Galerkin(MLPG) approach in computational mechanics[J]. Computational Mechanics, 1998, 22(2): 117−127.

[7]Gingold R A, Monaghan J J. Smoothed particle hydrodynamics:theory and application to non-spherical stars[J]. Monthly Notices of the Royal Astronomical Society, 1977, 181: 375−389.

[8]缪吉伦, 陈景秋, 张永祥. 基于 SPH 方法的立面二维涌浪数值模拟[J]. 中南大学学报(自然科学版), 2012, 43(8):3244−3249.MIAO Jilun, CHEN Jingqiu, ZHANG Yongxiang.Two-dimension numerical simulation of impulsive waves by SPH method[J]. Journal of Central South University (Science and Technology), 2012, 43(8): 3244−3249.

[9]Liu W K, Jun S, Zhang Y F. Reproducing kernel particle methods[J]. International Journal for Numerical Methods in Fluids, 1995, 20: 1081−1106.

[10]程玉民, 李九红. 弹性力学的复变量无网格方法[J]. 物理学报, 2005, 54(10): 4463−4471.CHENG Yumin, LI Jiuhong. A meshless method with complex variables for elasticity[J]. Acta Physica Sinica, 2005, 54(10):4463−4471.

[11]程玉民, 陈美娟. 弹性力学的一种边界无单元法[J]. 力学学报, 2003, 35(2): 181−186.CHENG Yumin, CHEN Meijuan. A boundary element-free method for linear elasticity[J]. Chinese Journal of Theoretical and Applied Mechanics, 2003, 35(2): 181−186.

[12]程玉民, 彭妙娟. 弹性动力学的边界无单元法[J]. 中国科学,2005, 35(4): 435−448.CHENG Yumin, PENG Miaojuan. Boundary element-free method for elastodynamics[J]. Science in China, 2005, 35(4):435−448.

[13]李树忱, 李术才, 朱维申. 弹性动力学的无网格流形方法[J].岩石力学与工程学报, 2006, 25(1): 141−145.LI Shuchen, LI Shucai, ZHU Weishen. Study on meshless manifold method in elastodynamics[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(1): 141−145.

[14]Sukumar N, Moran B, Belytschko T. The natural elements method in solid mechanics[J]. International Journal for Numerical Methods in Engineering, 1998, 43: 839−887.

[15]Gu L. Moving kriging interpolation and element-free Galerkin method[J]. International Journal for Numerical Methods in Engineering, 2003, 56: 1−11.

[16]Dai K Y, Liu G R, Lim K M, et al. Comparison between the radial point interpolation and the kriging interpolation used in meshfree methods[J]. Computational Mechanics, 2003, 32:60−70.

[17]Soares D Jr, Sladek J, Sladek V. Nonlinear dynamic analyses by meshless local Petrov-Galerkin formulations[J]. International Journal for Numerical Methods in Engineering, 2010, 81:1687−1699.

[18]陈莘莘, 李庆华, 刘应华, 等. 动力弹塑性分析的无网格自然单元法[J]. 固体力学学报, 2011, 32(5): 493−499.CHEN Shenshen, LI Qinghua, LIU Yinghua, et al. Application of meshless natural element method to dynamic elastoplastic analysis[J]. Chinese Journal of Solid Mechanics, 2011, 32(5):493−499.

[19]Owen D J R, Hinton E. Finite element in plasticity: Theory and practice[M]. Swansea: Pineridge Press, 1980: 431−463.