维氏压入压痕形貌仿真与实验分析

黄勇，马德军，陈伟，王家梁，孙亮

（装甲兵工程学院 机械工程系，北京 100072）

0 引言

随着纳米技术的发展，材料在微纳米尺度下的力学性能研究逐渐成为人们关注的热点。硬度作为材料多种力学特性的“显微探针”，与材料其他力学性能，如弹性模量、抗拉强度、剪切模量等存在一定的经验关系［1-3］，在对材料和工艺方法的研究中起着重要的作用［4］。通过硬度测量来检验材料、半成品和零件质量的这种方法，在机械制造、航空航天等现代工业中得到广泛的应用。然而，传统维氏硬度实验中需要肉眼对压痕形貌进行测量，不可避免地会遇到因压痕不够清晰导致的压痕形貌测量困难的问题，这在一定程度上影响了维氏硬度的测量准确性。此外，压痕形貌的准确识别对陶瓷材料的断裂韧性仪器化压入测试也具有至关重要的作用［5-6］。

为此，本文基于有限元数值分析模型对6061 铝合金维氏压入压痕形貌进行仿真，并与压痕实验测量结果进行比较。从而验证本文所提的有限元数值仿真方法对压痕形貌仿真识别结果的有效性，为进一步探索基于压痕形貌识别材料弹塑性参数的可能性提供技术基础。

1 6061 铝合金维氏压入有限元数值仿真

标准的四棱锥Vickers 压头面角为136°，其对材料进行的维氏压入产生的压痕形貌如图1 所示，其中d 为压痕对角线半长C1O1，l 为压痕中心与边沿距离A1O1。为了对维氏压入压痕形貌进行有限元数值仿真，本文以6061 铝合金为例，应用商用有限元软件Abaqus［7］建立维氏压入三维有限元模型。为降低计算成本，根据模型对称性可以取Vickers 压头的1/8 建立模型进行分析，被压材料也定义为与压头对称性相适应的1/8 模型。

图1 维氏压入压痕图

对于网格划分，靠近压头尖端的局部网格划分精细，远离压头的区域划分较为稀疏。考虑到有限元模型主要针对压痕对角线和压痕中心与边沿距离进行计算，特别对被压材料的压痕对角线和压痕中心与边沿区域网格进行精细划分，如图2 所示。通过网格收敛性分析和远场无关性分析，最终确定压头划分为23 828 个四面体单元，被压材料划分为54 720 个六面体单元和191 554 个四面体单元。根据6061 铝合金的标准单轴拉伸实验数据获得反映材料本构关系的真实应力—应变曲线，作为有限元数值仿真的材料属性进行输入，其中弹性模量为71 GPa，泊松比为0.33。金刚石Vickers 压头定义为弹性体，其中弹性模量为1141 GPa，泊松比为0.07。压头和被压材料的接触摩擦因数f 分别取0、0.15、0.30、0.50。整个6061 铝合金维氏压入仿真计算采用非线性大变形理论。

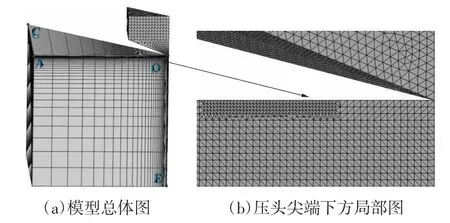
图2 维氏压入三维有限元模型图

对于压痕对角线半长与压痕中心与边沿距离的仿真结果识别，关键在于确定压头卸载后材料回弹完全恢复的压痕边缘有限元节点位置。本文确定压痕边缘有限元节点位置主要分为两步：第一步，当压头以最大压入载荷Pm压入6061 铝合金材料至最大压入深度hm时，确定出此时1/8模型在AOE 对称面和COE 对称面上压头与材料表面的接触边缘节点a、b，如图3 所示；第二步，当压头卸载后，识别接触边缘节点a、b 的坐标位置，从而得到压痕对角线半长和压痕中心与边沿距离的有限元数值仿真结果。

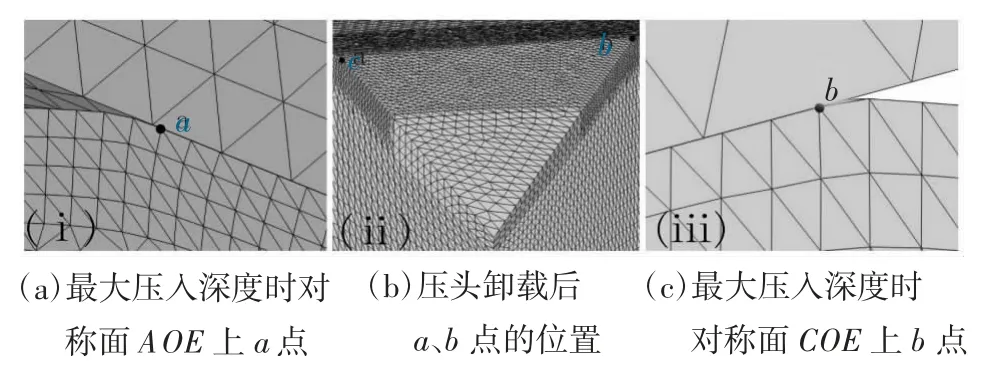
图3 压头与被压材料接触节点位置示意图

基于上述有限元仿真方法，对6061 铝合金材料进行维氏压入压痕的有限元数值仿真，固定压头最大压入深度hm1=5 μm，针对不同接触面摩擦因数对应的6061 铝合金维氏压入压痕仿真计算值如表1 所示，d1为有限元仿真的压痕对角线半长，l1为有限元仿真的压痕中心与边沿距离，σd1为有限元仿真的压痕对角线半长d1的变化范围，σl1为有限元仿真的压痕中心与边沿距离l1的变化范围。

表1 不同接触面摩擦因数对应的6061 铝合金维氏压入压痕有限元仿真结果（hm1=5 μm）

由表1 可以看出，在有限元仿真模型中，不同接触面摩擦因数（f=0、0.15、0.30、0.50）对6061 铝合金压痕对角线半长d1的影响较小，有限元仿真的压痕对角线半长d1变化范围σd1为4.556%；对压痕中心与边沿距离l1的影响较大，有限元仿真的压痕中心与边沿距离l1变化范围σl1为8.891%。其主要原因在于：摩擦因数对压痕边缘鼓凸或沉陷有着较大影响，而压痕边缘鼓凸或沉陷对压痕对角线半长d1测量的影响较小，对压痕中心与边沿距离l1测量的影响比较大。

2 6061 铝合金维氏压入实验

按照国际标准ISO14577［8］的要求制备6061 铝合金压入标准试样块。采用自主研制的具有完全自主知识产权的“高精度宏观仪器化压入仪”［9］对6061 铝合金进行维氏压入实验，所用四棱锥Vickers 压头的面角已经过标定。加载阶段的加载速率为0.5 N/s，最大压入载荷为50 N；保载30 s；卸载阶段的卸载速率与加载速率保持一致，为0.5 N/s。按照上述压入要求，重复实验5次，压痕之间保持适当距离，避免实验结果相互干扰。利用光学显微镜，对6061 铝合金维氏压入实验获得的压痕形貌进行观测，如图4 所示。各压痕参数量取数据见表2，其中hm2为实验材料最大压入深度的平均值，d2为压入实验真实压痕对角线半长的平均值，l2为压入实验真实压痕中心与边沿距离的平均值。

图4 6061 铝合金维氏压入实验获得的真实压痕形貌

表2 6061 铝合金维氏压入实验获得的压痕参数平均值 μm

3 6061 铝合金维氏压入有限元仿真与实验对比

由于维氏压入过程中，6061 铝合金与金刚石压头的实际接触摩擦因数f 难以确定，本文取不同接触面摩擦因数对应的6061 铝合金维氏压入有限元仿真获得的压痕形貌参数与实验真实压痕参数进行对比。维氏压头的对角线半长和深度之比为3.5，底面边长半长与深度之比为2.475。考虑有限元模型的无量纲性和维氏压入的自相似性，可以通过定义无量纲量对角线半长d 与深度h 之比δd和压痕中心与边沿距离l 与深度h 之比δl来反映有限元仿真压痕和实验压入压痕的一致性。其结果见表3，δd1为有限元仿真压痕对角线半长d1与最大压入深度hm1的比值，δl1为有限元仿真压痕中心与边沿距离l1与最大压入深度hm1的比值，δd2为实验真实压痕对角线半长d2与最大压入深度hm2的比值，δl2为实验真实压痕中心与边沿距离l2与最大压入深度hm2的比值。

表3 6061 铝合金维氏压入不同摩擦因数有限元仿真压痕参数与实验真实压痕参数对比数据

由表3 可知，在不同接触面摩擦因数（f=0、0.15、0.30、0.50）情况下，有限元仿真压痕对角线半长d1与最大压入深度hm1的比值δd1与实验真实压痕对角线半长d2与最大压入深度hm2的比值δd2的差别在0.52%～5.10%之间；有限元仿真压痕中心与边沿距离l1与最大压入深度hm1的比值δl1与实验真实压痕中心与边沿距离l2与最大压入深度hm2的比值δl2的差别在-3.62%～4.95%。当摩擦因数f 从0 到0.15 后，δd1与δd2的差别由5.10%减小到0.99%；δl1与δl2的差别也由4.95%减小到-0.75%。而当摩擦因数f 从0.15 增加到0.5 后，δd2与δd2的差别趋于稳定，δl1与δl2的差别又逐渐增大。而这主要在于实际压入的过程中，金刚石压头与6061 铝合金存在一定的摩擦，并且通常认为这个摩擦因数在0.15 左右。而摩擦因数对压痕边缘的鼓凸或沉陷影响较大，因而随着摩擦因数增加，压痕中心与边沿距离l1的测量准确性也受到了影响。因此本文认为上述有限元仿真模型中摩擦因数设置为0.15 时，仿真结果与实际维氏压入情况最为接近，其有限元仿真压痕对角线半长d1与最大压入深度hm1的比值δd1与实验真实压痕对角线半长d2与最大压入深度hm2的比值δd2的差别为0.99%，有限元仿真压痕中心与边沿距离l1与最大压入深度hm1的比值δl1与实验真实压痕中心与边沿距离l2与最大压入深度hm2的比值δl2的差别为-0.75%。

4 结论

本文采用有限元数值分析模型对维氏压入过程中产生的压痕形貌进行仿真。以6061 铝合金为例，对比其有限元仿真压痕与实验测量压痕的对角线半长和压痕中心与边沿距离。结果表明，6061 铝合金的有限元仿真压痕与实验测量压痕对角线半长和压痕中心与边沿距离差别分别为0.99%和-0.75%，且随着压头与材料间的摩擦因数由0变化至0.5，有限元仿真压痕与实验测量压痕的对角线半长和压痕中心与边沿距离差别分别变化为4.556%和8.891%。因此，材料维氏压入压痕形貌可通过有限元数值仿真的方法获得，从而解决了小载荷硬度测试情况下因压痕不够清晰导致的压痕形貌测量难题，为探索基于压痕形貌识别材料弹塑性参数的可能性提供技术基础。

［1］Chung H Y，Weinberger M B，Yang J M，et al.Correlation between hardness and elastic moduli of the ultrain-compressible transition metal diborides RuB2，OsB2，and ReB2［J］.Applied Physics Letters，2008，92：261904.

［2］Ramamurty U，Jana S，Kawamura Y，et al.Hardness and plastic deformation in a bulk metallic glass［J］.Acta Materialia，2005，53：705-717.

［3］Yang R，Zhang T H，Jiang P，et al.Experimental verification and theoretical analysis of the relationships between hardness，elastic modulus，and the work of indentation［J］.Applied Physics Letters，2008，92：231906.

［4］周益春，郑学军.材料的宏微观力学性能［M］.北京：高等教育出版社，2009：111-112.

［5］Evans A G，Charles E A.Fracture toughness determination by indentation［J］.J.Am.Ceram.Soc.，1976，59：371-376.

［6］Anstis G R，Chantikul P，Lawn B R，et al.A critical evaluation of indentation techniques for measuring fracture toughness：I，direct crack measurements ［J］.J.Am Ceram.Soc.，1981，64：533-538.

［7］ABAQUS Version 6.2［M］.Hibbitt，Karlsson &Sorensen Inc.，RI，2001.

［8］ISO 14577-2002 Metallic Materials Instrumented Indentation Test for Hardness and Materials Parameter［S］.

［9］马德军，宋仲康，郭俊宏，等.一种高精度仪器化压入仪及金刚石压头压入试样深度的计算方法：中国，CN102288500A［P］.2011-12-21.