自然环境温度作用谱和混凝土温度响应谱
2014-11-28余志武
刘 鹏,余志武,宋 力
(1.中南大学 土木工程学院,湖南 长沙 410075;2.中南大学 高速铁路建造技术国家工程实验室,湖南 长沙 410075)
自然环境因素是影响钢筋混凝土结构工程耐久性的重要外因之一[1-2],其中温度因素影响尤甚[3-4].在自然环境中,钢筋混凝土结构长期受到周期性季节交变气温和日照温差作用,因其非良导热性使得内外存在较大温差即温度梯度,产生温度应力,导致结构开裂、性能劣化和使用寿命缩短[5-6];国内外有关温度对钢筋混凝土工程的影响已展开了大量研究,并取得了许多研究成果[7-11].Luikov[12]基于Fourier定律研究了混凝土中的温度传输与分布规律,建立了基于温度和水汽的传输模型;Qin 等[13]采用动态模型评估了建筑材料瞬态热和水汽传输行为,利用Laplace变换与TFM 法建立了相应的温度和水汽分布模型;蒋建华等[14]采用有限极差法建立了自然环境温度模型及其混凝土响应模型;曹为民等[15]应用非稳定温度场和徐变应力场仿真程序对裂缝产生的原因进行了探讨.尽管这些模型可描述混凝土内部的温度变化规律,但仍存在精度、初始条件、边界条件和求解等问题.如何简单、精确地表征自然环境作用谱及其混凝土内的响应规律是当前研究的难点.此外,影响混凝土结构耐久性的温度是混凝土内部微环境温度而非自然环境温度.为合理预测自然环境下钢筋混凝土结构的耐久性和使用寿命,有必要展开自然环境温度作用谱和混凝土温度响应规律方面的研究.
本文通过理论分析建立了自然环境温度作用谱模型,利用试验测试结果和分段拟合法构建了相应的作用谱,并基于历年气象资料对其合理性和普适性进行了验证.基于自然环境作用谱模型,分析了混凝土内部微环境温度响应规律,建立了混凝土温度响应谱模型,并通过试验测试对其进行了验证.此外,还对混凝土温度响应简化处理方法进行了论证,为混凝土耐久性和使用寿命的预测提供了理论依据.
1 理论推导
1.1 自然环境温度作用谱
因自转和公转使地球表面接受的太阳辐射能量可采用余弦(或正弦)函数表示[16],而这些能量又通过辐射、对流和传导等形式传输到大气中,故自然环境温度亦可采用相同的函数予以表征,本文假设自然环境温度的变化规律为:
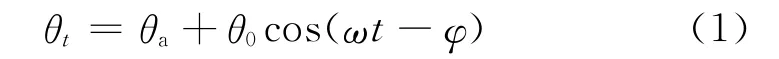
式中:θt为t时刻的温度值,℃;θa为自然环境温度波的平均值,℃;θ0为自然环境温度变化幅值,℃;ω为地球公转角频率,rad/s;φ 为相位角,rad.
既有研究多采用式(1)表征1d内的温度变化规律.但是,地球公转使不同季节的日照时间不同,故采用单一形式表征温度的变化会带来较大误差.本文拟考虑地球公转对温度波动周期T(从最低温度升至最高温度的时间)的影响,采用分段形式来表征自然环境温度的变化规律,即将日温度变化曲线分为升温和降温曲线,相应的温度理论模型如式(2)所示.

式中:tmin为日最低气温时刻,h;T 为14-tmin,h.
每天自然环境最低温度出现的时间为日出前后,可由相应的白昼时间y(h)求出,即:
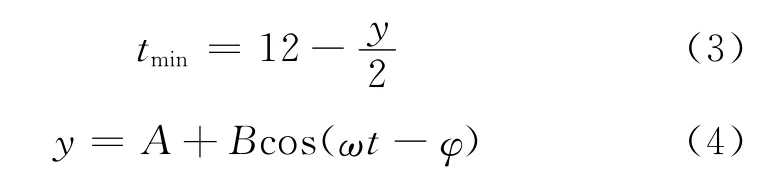
式中:A 为白昼时间的平均值,h;B 为白昼时间的幅值,h.
1.2 混凝土温度响应谱
循环温度荷载作用下半无限体内部的温度场是一个不断变化的非稳态过程,当时间足够长时,将进入准稳态简谐波动过程,其差异仅表现为波幅的衰减和滞后.鉴于篇幅所限,关于混凝土温度响应预计模型和参数取值的研究内容已另文阐述,相应的混凝土温度响应模型如式(5)所示.
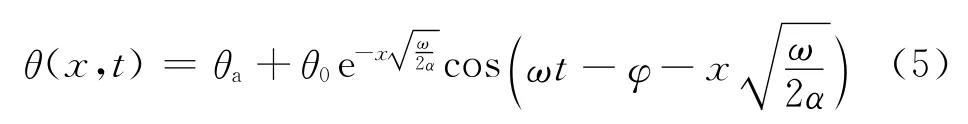
式中:θ(x,t)为t时刻混凝土内x 深度处的温度值,℃;α 为热扩散系数,m2/s,α=λ/ρc(ρ 为导热体密度,kg/m3,取ρ=2 300kg/m3,c 为导热体比热容,J/(kg·K),取c=920J/(kg·K),λ 为导热系数,W/(m·K),取λ=2.0W/(m·K)).
相应的混凝土温度响应模型可用式(6)表示.
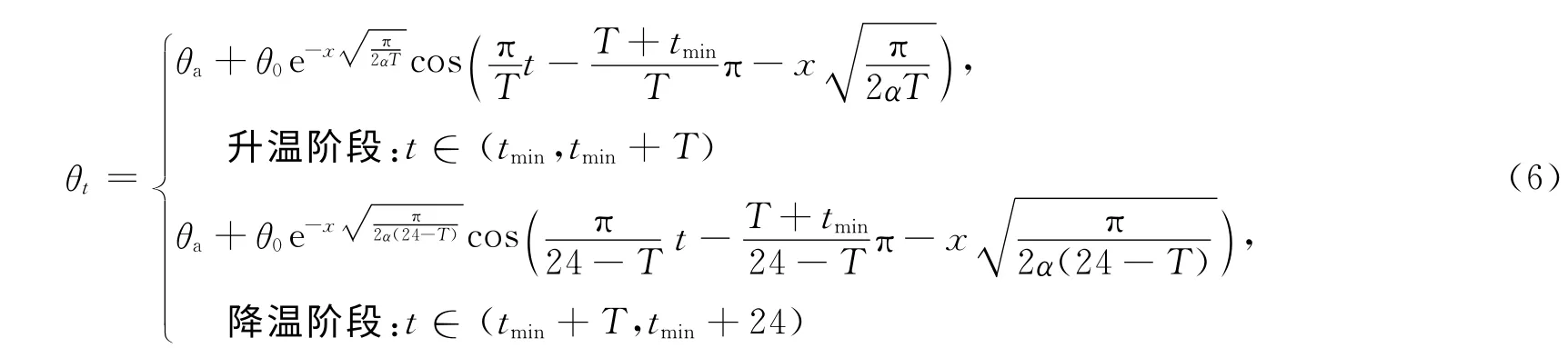
式(2),(6)分别为本文建立的自然环境温度作用谱模型和相应的混凝土温度响应谱模型.
2 试验
2.1 原材料、配合比及试验仪器
主要原料:长沙平塘水泥厂产P·O42.5水泥;长沙黄腾外加剂厂生产聚羧酸系列高效减水剂;湖南湘潭电厂Ⅰ级粉煤灰;湖南涟源钢铁集团有限公司生产S95级矿粉;长沙本地产河砂,细度模数约2.9;连续级配石灰岩碎石,粒径5~20mm;自来水.拟配制C30 级混凝土,其m(水泥)∶m(矿粉)∶m(粉煤灰)∶m(砂)∶m(石)∶m(水)∶m(减水剂)为290.0∶50.0∶60.0∶730.0∶1 050.0∶164.0∶4.2.温度测定仪为湖南省长沙市三智电子科技有限公司生产的SHT10温湿度传感器.
2.2 试样制作与试验过程
按照JTG E30—2005《公路工程水泥及水泥混凝土试验规程》中的T0553—2005《水泥混凝土立方体抗压强度试验》进行试验.试样尺寸为150mm×150mm×150mm 立方体,成型24h后脱模,放入标准养护池中养护至试验龄期,其实测抗压强度为34MPa.采用钻芯机从试样侧面取芯,制成直径为(100±1)mm,高度为(150±1)mm 的圆柱体,然后,钻取距离表面深度为5,15,35mm 的孔,将温度传感器置入,并采用相同级配的混凝土浆体密封,养护7d后,将试样置于杜瓦瓶中,采用相同级配的混凝土浇筑成型、养护.根据测试要求,将试样长时间(不少于3 个月)置于所测环境中,使其内部的温湿度基本稳定.图1 为混凝土温度响应模型试件示意图.在测试过程中,将试样置于四周空旷且距地面高度约为1.5 m 的百叶箱中,传感器一端连接测定仪,大约每30min读取1 次温度值,记录不同时刻的自然环境温度值和混凝土内不同深度的温度值.
3 分析与讨论
3.1 T 的确定
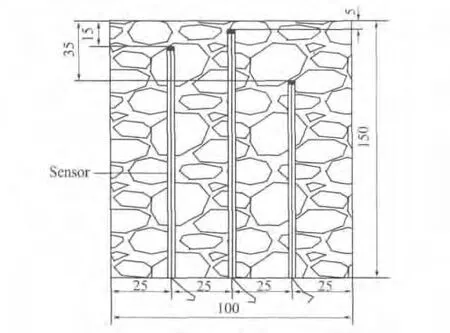
图1 混凝土温度响应模型试件示意图Fig.1 Model of temperature response in concrete(size:mm)
季节和纬度差异造成了不同地方的日出时间不同,自然环境温度作用谱模型首先需求解相应周期参数.鉴于太阳在每年12 月21 日至23 日将直射到地球的南回归线附近,故本试验拟选取每月第21日的白昼时间作为参数.以北京、天津和长沙3个地区为例,对全年白昼时间进行了拟合,如图2所示.
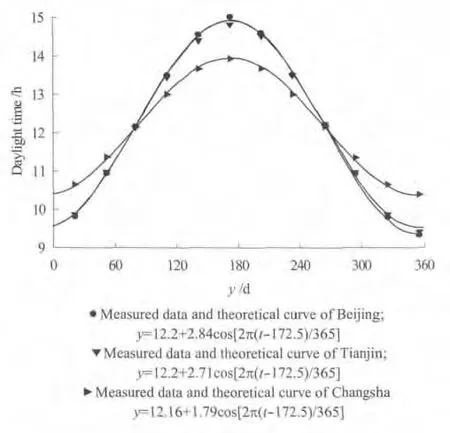
图2 3个地区全年每天的白昼时间Fig.2 Daylight time of three region in a year
从图2可以看出,采用余弦函数可很好拟合不同地区全年每天的白昼时间,从而验证了温度波动周期理论模型的正确性.在温度波动周期理论模型中代入日期参数,可求得相应的白昼时间,进而获得所需的T.从图2还可以看出,纬度间的差异主要体现为相应函数表达式中的参数取值不同.对于相近纬度(如北京和天津)地区全年每天的白昼时间大致相等,故其函数表达式的各参数基本一致,而不同纬度地区(如北京和长沙)全年每天的白昼时间相差明显,相应函数表达式的各参数有较大差别.对于高纬度地区(如北京)昼夜时间长短波动较大,白昼最长可达到15h,最短只有9.4h,而低纬度地区(如长沙)白昼最长为14h,最短为10.4h.这种差异造成了各地区昼夜温差的变化,是昼夜自然环境温度波动的重要因素.
3.2 自然环境温度作用谱
以长沙地区为例,采用温湿度传感器测定不同时间的自然环境温度变化,进而验证自然环境温度作用谱模型的合理性.测试时间为2011年8 月16日至2011年8月19日,天气晴朗、微风,测试结果及其理论模型曲线如图3所示.
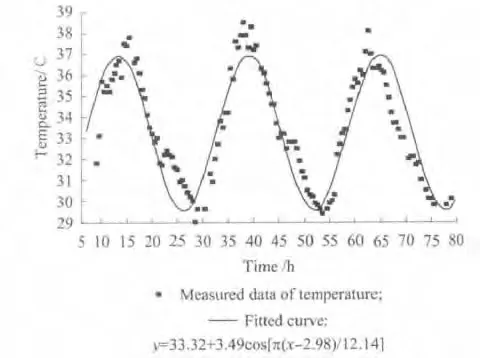
图3 自然环境温度变化及拟合曲线Fig.3 Change of natural environment temperature and its fitted curve
从图3可以看出,自然环境温度变化呈周期性波动,其变化周期为24h.采用余弦函数拟合的曲线与实测温度变化趋势吻合,验证了基于余弦函数建立的温度波动周期理论模型的合理性.自然环境温度随日出逐渐升高,最高气温出现在每天的午后14:30左右,随日落逐渐降低,最低气温出现在次日的凌晨05:30左右.众所周知,太阳向地球辐射的能量在每天的12h达到最强,但地面将所吸收的热量传输给空气需要一定时间,故自然环境最高温度出现的时间滞后.从图3还可以看出,自然环境降温过程持续时间大于升温过程,其温度变化率相对较小.余弦函数拟合曲线与实测数据偏离过大是由于昼夜时间不等所致.为了克服自然环境温度作用谱模型的局限性,本文建立了余弦函数分段表达式模型.图4为长沙地区自然环境温度变化拟合曲线,测试期间的日平均温度为33.6℃,日温差幅值为8.1℃,升温阶段T 为8.5h.
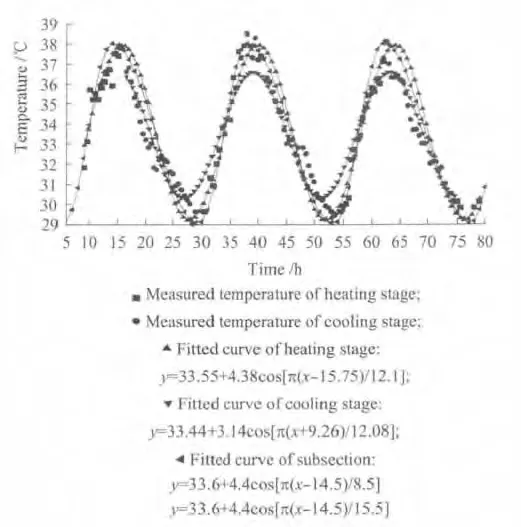
图4 自然环境温度变化拟合曲线Fig.4 Fitted curve of natural environment temperature
从图4可以看出,自然环境温度日变化曲线可分为升温和降温2个阶段,对升温和降温阶段的自然环境温度分别采用余弦函数模型拟合,其吻合程度和相关性更佳.至于图4中仍有部分点不能与分段拟合曲线吻合,是由于自然环境温度作用谱模型的参数为测试数据的平均值所致.从图4还可以看出,基于自然环境温度作用谱模型和实测环境温度极值所绘制的曲线,可表征相应温度波动趋势和变化量.鉴于此,基于2009年9月自然环境的最高和最低温度及其月均温度,采用分段函数形式进行了拟合,结果如图5所示.
从图5可以看出,基于日最高、最低温度参数和自然环境温度作用谱模型拟合曲线可表征日温度波动规律、周期及波动幅值,可获得每天相应时刻的自然环境温度;基于月均温度参数的拟合曲线亦可反映相应期间自然环境温度的整体波动特征.通过分析对比可知:每天的自然环境温度特征应基于每天的温度参数拟合表征,月均自然环境温度特征应基于月均温度参数拟合表征.
3.3 混凝土内温度响应谱
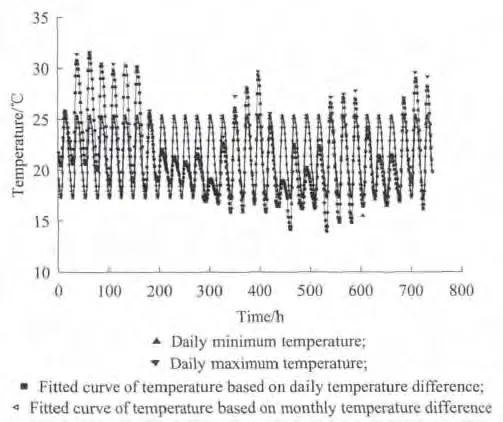
图5 长沙地区2009年9月自然环境温度变化拟合曲线Fig.5 Fitted curve of natural environment temperature in Sep.2009in Changsha area
以长沙地区2011年8月16日至2011年8月19日为例,采用温湿度传感器测试了混凝土内不同深度处温度变化.为更好了解混凝土内温度响应规律,首先探讨了自然环境温度作用下混凝土内35mm处的温度响应规律,如图6所示.图7为混凝土内不同深度处的温度变化曲线.
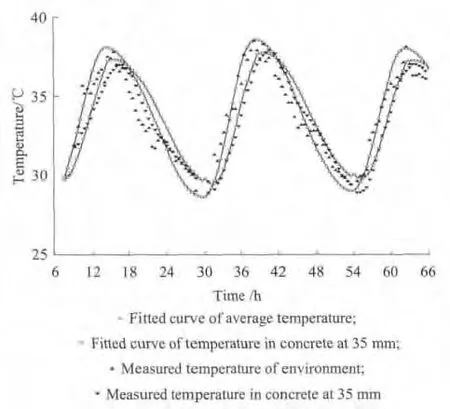
图6 自然环境温度作用下混凝土温度响应Fig.6 Temperature response of concrete under the effect of natural environment temperature
从图6可以看出,自然环境温度的变化与混凝土温度响应存在较大的相关性,两者变化趋势基本一致.与自然环境温度作用谱相比,混凝土温度响应波动曲线略有差别,主要表现为曲线相对光滑、温度波动滞后和幅值衰减等方面.当自然环境处于升温阶段时,混凝土温度低于外部环境温度,而降温阶段则相反.两者的温度波动周期频率相同,说明混凝土自身特性不改变外界温度作用频率.混凝土内部温度变化幅值有所降低是由于混凝土的密度、热传导系数和比热容与自然环境的差异导致了延滞和衰减.从图6中还可以看出,混凝土温度响应谱模型拟合曲线与实测温度曲线吻合较好,表明该模型合理、可靠.
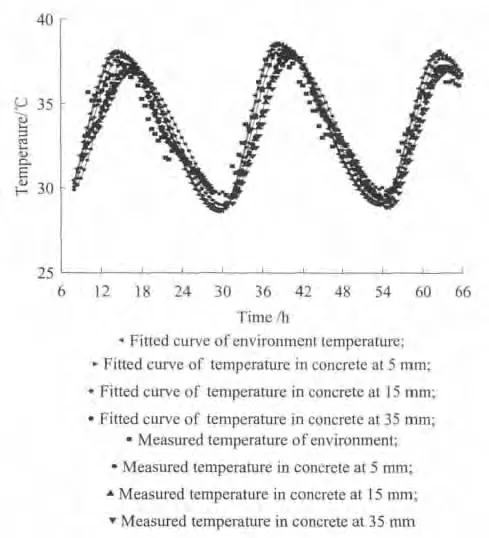
图7 混凝土内不同深度处的温度响应Fig.7 Temperature response at the different depths of concrete
从图7可以看出,混凝土不同深度处的温度响应规律基本一致,均随自然环境温度周期性波动,且与理论模型拟合曲线吻合较好.混凝土温度响应的滞后时间随混凝土的深度增加而延长,而相应的温度响应幅值则随之减小,这是因混凝土的热阻效应所致.在每1个温度波动周期内,不同曲线均存在2个交叉点,当曲线处于高温与低温阶段的交叉点之间时,相应的表层混凝土温度高于其深处温度;当曲线处于低温与高温阶段的交叉点之间时,相应的表层混凝土温度则低于其深处温度.混凝土深度越大,交叉点出现的时间越滞后.综上可见,混凝土温度响应谱模型可较好描述自然环境温度的作用.图8为2009年9月自然环境温度作用下混凝土35mm 处的温度响应谱.
从图8可见,基于自然环境日最高与最低温度和混凝土温度响应谱模型拟合曲线可以准确表征混凝土内部的温度波动规律,通过拟合曲线可获得每天相应时刻自然环境温度作用下的混凝土内部的温度值.这为人工模拟试验中温度参数的确立提供了理论依据.
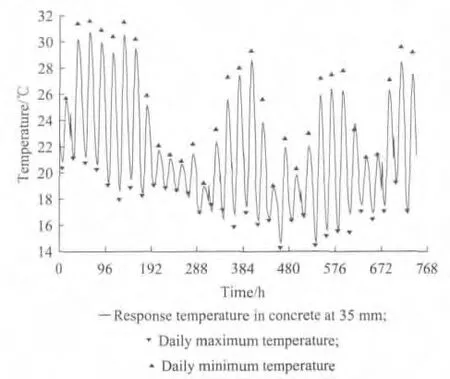
图8 自然环境温度作用下混凝土温度响应谱Fig.8 Spectrum of temperature in concrete under the effect of natural environment temperature
4 结论
(1)自然环境温度变化呈现出周期性波动,可分为升温和降温2个过程;基于分段的余弦函数形式建立的自然环境温度作用谱可表征自然环境温度波动规律和特征,相应的拟合曲线与测试结果吻合较好.
(2)混凝土内部的温度响应与自然环境温度变化密切相关,两者的相同之处表现为温度波动趋势和周期一致,其差异则主要表现为温度滞后和幅值衰减.
(3)混凝土温度响应滞后时间随其深度的增加而延长,而温度波动幅值则随其深度的增加而减小;基于自然环境温度作用谱模型建立的混凝土温度响应谱可表征混凝土内部的温度波动情况,利用自然环境温度作用谱中的参数可表征混凝土不同深度处的温度响应.
[1]ABAHRI K,BELARBI R,TRABELSI A.Contribution to analytical and numerical study of combined heat and moisture transfers in porous building materials[J].Building and Environment,2011,46(7):1354-1360.
[2]TB 10002.3—2005 铁路桥涵钢筋混凝土和预应力混凝土结构设计规范[S].TB 10002.3—2005 Code for design on reinforced and prestressed concrete structure of railway bridge and culvert[S].(in Chinese)
[3]CHANG Winjin,WENG Chengi.An analytical solution to coupled heat and moisture diffusion transfer in porous materials[J].International Journal of Heat and Mass Transfer,2000,43(19):3621-3632.
[4]QIN M H,RAFIK B,ABDELKARIM A M,et al.Coupled heat and moisture transfer in multi-layer building materials[J].Construction and Building Materials,2009,23(2):967-975.
[5]付春雨.混凝土梁桥的温度场与温度应力研究[D].成都:西南交通大学,2006.FU Chunyu.Research on the temperature field and temperature stress of the concrete bridge[D].Chengdu:Southwest Jiaotong University,2006.(in Chinese)
[6]BURKAN I O,GHANI R A.Finite element modeling of coupled heat transfer,moisture transport and carbonation processes in concrete structures[J].Cement and Concrete Composites,2004,26(1):57-73.
[7]HAUPL P,GRUNEWALD J,FECHNER H.Coupled heat air and moisture transfer in building structures[J].International Journal of Heat and Mass Transfer,1997,40(7):1633-1642.
[8]WONG J M,GLASSER F P,IMBABI M S.Evaluation of thermal conductivity in air permeable concrete for dynamic breathing wall construction[J].Cement and Concrete Composites,2007,29(9):647-655.
[9]SCHNIDLER A K,RUIZ J M,RASMUSSEN R O,et al.Concrete pavement temperature prediction and case studies with the FHWA HIPERPAV models[J].Cement and Concrete Composites,2004,26(5):463-471.
[10]刘光廷,焦修刚.混凝土的热湿传导耦合分析[J].清华大学学报,2004,44(12):1653-1655.LIU Guangting,JIAO Xiugang.Coupled heat and moisture transfer analysis of concrete[J].Journal of Tsinghua University,2004,44(12):1653-1655.(in Chinese)
[11]GERSON H S,NATHAN M.Heat,air and moisture transfer through hollow porous blocks[J].International Journal of Heat and Mass Transfer,2009,52(9):2390-2398.
[12]LUIKOV A W.Heat and mass transfer in capillary-porous bodies[M].Oxford:Pergamon Press,1966:6.
[13]QIN M H,RAFIK B,ABDELKARIM A M,et al.An analytical method to calculate the coupled heat and moisture transfer in building materials[J].International Communications in Heat and Mass Transfer,2006,33(1):39-48.
[14]蒋建华,袁迎曙,张习美.自然气候环境的温度作用谱和混凝土内温度响应预计[J].中南大学学报,2010,41(5):1923-1930.JIANG Jianhua,YUAN Yingshu,ZHANG Ximei.Action spectrum of temperature in natural climate environment and prediction of temperature response in concrete[J].Journal of Central South University,2010,41(5):1923-1930.(in Chinese)
[15]曹为民,吴健,闪黎.水闸闸墩温度场及应力场仿真分析[J].河海大学学报,2002,30(5):48-52.CAO Weimin,WU Jian,SHAN Li.Numerical simulation of temperature field and stress field of sluice piers[J].Journal of Hohai University,2002,30(5):48-52.(in Chinese)
[16]朱伯芳.大体积混凝土温度应力与温度控制[M].北京:中国电力出版社,1998:10-13.ZHU Bofang.Thermal stresses and temperature control ofmass concrete[M].Beijing:China Electric Power Press,1998:10-13.(in Chinese)
