培养学生运算能力 夯实学生数学基础

梁肇方

（白土镇初级中学，广东 高要 526109）

培养学生运算能力 夯实学生数学基础

梁肇方

（白土镇初级中学，广东 高要 526109）

随着科学技术的发展和社会的进步，计算机在家庭中的普及率越来越高，学生对电脑的依赖性起来越强，很多运算问题依靠电脑解决，这在无形中削弱了学生的运算能力。21世纪需要应用型、高智能人才，数学教师应善于在教学中培养学生的运算能力，夯实其数学基础。

初中数学；运算能力；分析能力；理解能力；思想方法

数学运算能力是一项基本的数学能力，通过有效的教学使中学生具备一定的数学运算能力，是中学数学教学的一项重要任务。新课程标准将培养学生的运算能力作为发展智力、培养能力的重中之重。随着科学技术的发展和社会的进步，计算机在家庭中得到普及，学生在解决许多运算问题时都依赖于电脑，这造成学生的运算能力严重不足。21世纪需要的是应用型、高智能的人才，这就要求我们数学教育工作者，在教学中不仅要向学生传授知识，也要注重技能培养，学生运算能力的培养就是其中的重点之一。教师要切实转变教学观念，着力培养学生的运算能力，努力夯实学生的数学基础。

一、学生运算能力培养中存在的问题

现在很多学生过度依赖于计算器，而且对计算的重视程度不够，由此导致中学生的数学运算能力普遍较差，其主要表现为运算的准确性差、速度慢以及运算的条理性不明。中学生运算能力发展的滞后，直接制约了其综合能力的提高。

（一）运算准确度较差

例1 计算：-34+(5-8)2-2×(-1)3。

错解 原式=81+(-3)2-2×(-1)=81+9+2=92。

分析：此题出错原因在于学生把-34当作了(-3)4，-34表示为34的相反数，其结果为-81;(-3)4的结果则为81。由此看出学生运算的准确度较差。学生在解题时，一定要注意到“乘方的相反数”和“相反数的乘方”之间的异同。

（二）运算速度慢

例2 将(-sin30°)-2,这3个实数按从小到大的顺序排列，正确的结果是（ ）

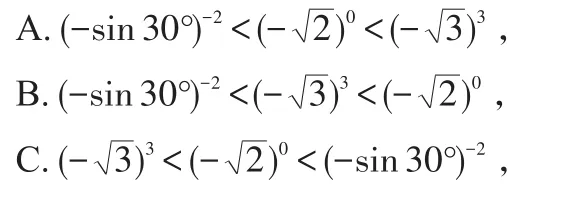
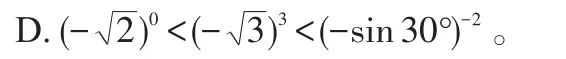
分析:比较这3个实数大小的一般办法是先计算出各式的结果，然后比较其大小。此题计算时易出错，且计算速度较慢；最佳方法是判断其值的正负，而不计算每个实数的结果。因为非0数的偶次幂为正数，所以(-sin30°)-2为正数；因为非0数的零次幂为1，所以的结果为1；因为负数的奇次幂为负数，因而的结果为负数，所以有，故选C。

（三）运算条理不清晰

例3 用因式分解法解方程2(x-2)2=x2-4。

错解 将右边分解因式，得2(x-2)2=(x+2)(x-2),方程两边同除以(x-2)，得2(x-2)=(x+2)，解得x=6。

分析：方程两边同乘以或除以同一个不为0的整式，方程的解不变。在上面的计算过程中，方程两边都除以(x-2)，但是(x-2)的值可能为0，这种计算方法会丢掉某一个解，属于条理不明晰。

二、学生运算能力的培养

教师如何在教学中有效培养学生的运算能力，是一个值得深入探究的问题。笔者在教学中非常重视问题分析以及学生对概念的理解，注重渗透数学思想方法，旨在通过高效教学达到事半功倍的效果。

（一）善于分析是提高运算能力的根本

1.直观分析。教师应通过直观的图表、演示、操作等，分析、揭示运算的本质，使学生从本质上认识数学，掌握好运算方法，准确地分析和解决数学问题。直观分析也是发展学生思维能力的方法之一。

例4 笔者在讲授“一元二次方程根与系数”的关系时，借助了表1。

表1 一元二次方程根与系数的关系示例

学生填写表1前，教师先引导学生观察表1中方程的特点：前4个方程一次项系数和常数项都是具体的数，第5个方程一次项系数与常数项是字母；5个方程的二次项系数都是1，前4个方程可用十字相乘法也可用配方法求解，第5个方程则用配方法求解。分析之后让学生动手计算各题结果。教师随后引导学生观察计算结果：各题的“两根之和”与“一次项系数”仅正负号不同；“两个根之积”与“常数项”完全相同。由此可以直观比较出“两根之和”与“一次项系数”的关系，以及“两根之积”与“常数项”的关系，并推广得出一般性“二次项系数为1”的一元二次方程的根与系数的关系，从而让学生深刻理解其关系的内涵，使学生在直观中寻找并掌握其运算规律。

2.对比分析。教师在教学中应将多种计算方法进行对照比较，从中启发学生，使其巩固学习成果，理顺思路，使学生的思维能力得到发展。

分析：此题如果想由已知比例式解出a,b,c的值，然后代入所求代数式中求值，则是无解的。因为a,b,c的具体值根本无法由已知比例式求得，由此可知解此题必须另辟蹊径。

依照惯例分析，可采用以下解法1。

说明：用此方法计算时，设这些比例的比值为k，得到用k的代数式表示a,b,c的公式，然后利用a,b,c中都有相同的因式k，对分式约分去掉未知数k，从而得出结果。这种数学思想方法很重要，对解决许多数学问题都有帮助，教师在教学时要让学生对此进行认真体会。

解完此题后，教师还要启发学生思考如下问题：除了这一解法，是否还有其他解法？学生在讨论交流后，可得出以下3种解法。

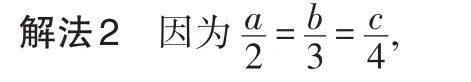
故不妨取特殊值a=2,b=3,c=4,

说明：此方法采取的是特殊值法，即把比例式中的字母取满足条件且较简单的特殊值，再将这些值代入所需求值的代数式中，即可得解。但有一点需提起注意：应用该方法给字母取值时，不具有普遍性，即字母取值本身有多种情况，而此处仅取一特例，让人觉得过于特殊化，因此这种方法具有一定的局限性，只适用于不需写过程而只要结果的填空题或选择题的解答。从另一方面说，在特殊情况下，此方法也是完全可行的。

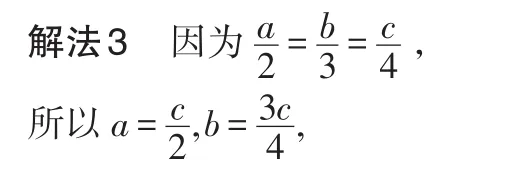
再将a和b代入所求代数式中，得其值为。

说明：此方法是通过已知比例式，把a,b,c都化成含c的代数式表示，代入所需求值的代数式后，通过分式将字母c约去，从而得出结果。解此题也可将a,c用含b的代数式表示，或将b,c用含a的代数式表示，之后代入代数式中求解。

第1，3，4种解法不仅适用于解填空题和选择题，还适用于需要写出解题过程的其他题型，具有普遍适用性，学生容易理解。解法2虽然具有一定局限性，但方法新且计算速度快，有时甚至可以不动笔仅略加思考即得到答案，因此与其他方法相比各有千秋。通过对比教学，可以使学生认识到求代数式的值可以采用不同方法，有的方法简捷，有的繁难，但是经过这种训练，学生思考问题的角度得到变换，思维方法得以拓展，这有助于提高学生思维的灵活性。

3.联系分析。将两个以上的事物按照一定顺序，为达到一定目的而进行细致的观察，找出事物之间的联系或变化规律。

对两项之间的联系进行分析：

(2)要使两个非负数的式子之和为0，必须令2x+3y+1=0及x-2y+1=0,从而将两个方程联立建成方程组，求出x与y的值。

通过联系分析，可找到已知等式中二次根式与绝对式内两个式子的联系，从而可求出x与y的值。

4.探究分析。

例7 一个两位数等于其个位数的平方，其个位数比十位数大，求这个两位数。

这道题显然应通过列方程组求解，但关键是如何写出这个两位数。教师可引领学生进行以下探索分析：

12=1×10+2,23=2×10+3,37=3×10+7，…

从而找出写出这个两位数的方法：设这个两位数的个位数为y,十位数为x,则这个两位数可以写成：10x+y,最终依照题意可以列出方程组进而求出这个两位数。

上述这些分析方法都是在数学教学中较为常用的分析方法，教师若能在课堂教学中有意识地穿插使用这些方法，则对培养学生的运算能力颇有助益。

（二）理解概念是提高运算能力的前提

当学生面对数学运算题时，要得到正确的运算结果，首先要正确理解概念，熟记重要的公式、法则及定理，准确无误是对运算的基本要求。正确记忆公式和法则是准确运算的前提，除此之外，还要掌握公式的推导方法。只有理解相关概念并掌握公式的推导，才能做到对公式的正用、反用和活用，从而提高运算能力。教师要让学生充分理解和掌握与运算相关的基础知识，这样才能减少其运算的出错率。

在学习分式这部分内容时，教师最好能用与分数类比的方法导出分式概念、分式的基本性质与四则运算法则，具体引入方法如下：

首先，先引领学生复习小学学过的分数概念：两数相除，可以表示成分数的形式。例如：。一个分数由分子、分母和分数线构成，分子、分母都是数，但分母不能是零。由于零不能做除数，故分母不能为零。分数有正分数、负分数，如果分子等于零，只要分母不是零(不论是正数还是负数)，这个分数的值即为零。教师可顺势将分数的概念引伸到代数式中，让学生观察这两个式子有什么特点并作出总结：(1)分式由分子、分母与分数线构成；(2)分母中含有字母的就是分式。在很自然地引入分式的概念后，指出分数与分式的区别所在：分数与分式形式相同，但分式中的分子、分母均为整式，且分母是含有字母的整式。

其次，教师在讲解分式的基本性质时，应先引领学生复习分数的基本性质，由此推想分式的基本性质。比如，计算不同分母分数的加法：,这里先将异分母化为同分母，。这样运算是根据分数的基本性质：分数的分子与分母都乘以（或除以）同一个不等于零的数，分数的值不变。分式是一般化了的分数，因此，分式应该有,这里，A,B,M是整式.根据分式的概念应该要求B≠0,由分数的基本性质应该想到M≠0。由此可得：分式的基本性质是分式的分子与分母都乘以(或除以)同一个不等于零的整式，分式的值不变。

最后，分式的四则运算顺序也可以类比分数进行，先做括号内的运算，然后再进行乘除运算，最后进行加减运算，这一顺序和步骤正是分式四则混合运算的顺序和步骤。四则混合运算法则概括地说就是：“先乘除，后加减，先进行括号内运算。”

通过对同类知识或不同类知识的比较，可以使学生对概念的理解更深刻，由此减少学生因对概念理解不透彻而出现的运算错误，从而强化学生的运算能力。

（三）掌握数学思想方法是提高运算能力的保证

计算能力的提高非一朝一夕之功可以成就，它需要长期的培养和训练。这就要求教师在平时的教学中，应加强计算能力的教学，而渗透数学思想方法是提高计算能力最有效、最实际的教学手段。只有让学生真正掌握了数学思想方法，才能提高其运算能力，达到夯实基础的目的。

在讲授完全平方公式时，教师可先给出以下问题：

例8 一块边长为a的正方形，将其边长增加b米，形成一个新的正方形，请用不同形式表示新的正方形的面积S。

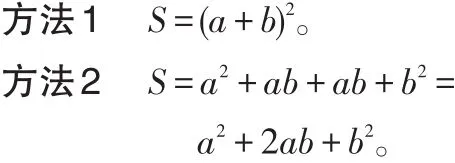
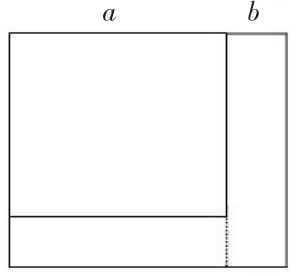
图1 示意图

从图1中可以看出，直接计算大正方形的面积，与把大正方形分成一个小正方形和两个长方形面积之和计算，其结果是一样的。采用两种思路计算正方形的面积，由面积相等可得出等式成立，由此就能简明扼要地推导出完全平方和公式：(a+b)2=a2+2ab+b2。

由此可见，对一些难以理解、枯燥无味的字母公式或法则，可以通过数形结合的方法得出规律，这样可以使学生更清晰、更直观地认识运算公式或法则。例8的解法特点是使用分割面积的数形结合方法，帮助学生直接理解问题，其过程简明扼要，易懂且易理解，可以使学生的观察与分析能力得到锻炼和提高。

综上所述，教师在教学中应着重培养学生的运算能力，夯实数学基础，充分激发学生在学习中的主动性和积极性。只有这样，才能培养出具有创造性能力的人才。而创造性人才的培养，不仅关乎我国科学技术水平的提高，也关系到我国科教兴国战略的成败。作为人民教师，我们任重而道远！

(责任编辑:陈 静)

梁肇方,男,广东省高要市白土镇初级中学,数学中学一级教师。