数形结合思想在数学教学中的应用

廖顺乔

（金渡镇华侨初级中学，广东 高要 526108）

数形结合思想在数学教学中的应用

廖顺乔

（金渡镇华侨初级中学，广东 高要 526108）

数形结合、函数与方程、转化与化归和分类讨论，是常见的重要数学思想方法。数形结合分为以形助数、以数助形以及数形互化，它有直观性，可使抽象问题形象化，复杂问题简单化。通过图形和数之间的关系，达到数、形互化，从而提高学生的分析问题，解决问题的能力。

初中教学；数形结合；以形助数；以数助形；互化

初中数学教材的内容可分为两部分，一部分是数，一部分是形，它们之间是互相联系的。我国著名数学家华罗庚曾说过：“数形结合百般好，隔离分家万事休，几何代数统一体，永远联系莫分离”。数形结合和函数与方程，转化与化归，分类讨论，是常见的重要数学思想方法。数形结合思想可使某些抽象的数学问题直观化、形象化，有助于把握数学本质，有利于数与形的信息相互传递。使用数形结合的思想方法，不但可以开拓学生的思维和视野，还可以培养他们的数学思想意识，达到胸中有图，见数想图的境界。数结形合的思想在初中多个章节都有充分的体现。

一、以形助数，使数量关系形象化

（一）由数变形，数量关系的几何意义

数形结合就是把抽象的数学语言与直观的图形结合起来，由数转化为形，构造出图形，用它的几何意义分析其代数意义。在实数中，实数与数轴是密不可分的，是数和形的结合体。利用数轴的直观性获得答案，可以体会数形结合的作用，认识到数与形是一种对应关系。

例1a、b在数轴上的位置(图1)所示，那么化简的结果是( )。

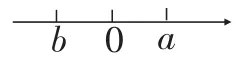
图1

A、2a-b;B、b;C、-b;D、-2a+b.

分析：先由数轴判断实数a、b的正负，对a、b进行大小比较，由数轴上表示的两个数，右边的数总比左边的数大，认识到数与形一种对应关系得知a＞0,b＞0,得a＞b,再判断a-b的正负，即a-b＞0,并根据绝对值的几何意义化简，最后合并同类项。所以

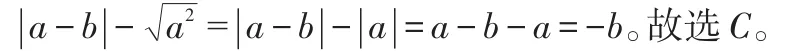
有理数的大小比较，相反数的几何意义，绝对值的几何意义，无理数的几何意义等，可利用数轴充分显示数与形结合起来产生的作用，抽象与形象的结合，能使学生的思维清晰。实数的有关数量问题比较抽象，难以把握，如果依赖“形”的直观性优点解决问题，问题就变得简单了。

（二）以形助数，数量关系向图形转化

把抽象的数学语言转化为直观图形是数形结合思想在数学中的应用方法之一。若无“形”，可通过构造或联想，正确绘制图形，反映图形中相应的数量关系，减少纷繁复杂的计算。初中数学教材中的方程、不等式都与函数知识有直接的联系，可以利用数形结合的思维方法，处理函数与方程、函数与不等式的关系。方程、不等式与函数间的抽象、复杂的数学问题借助了形的直观，就可以体会到数与式之间的相互联系、相互转化。

例2是否存在这样的实数k，使二次方程x2+(2k-1)x+(3k+2)=0，有两个实根且两根都在2，4之间？如果有，试确定k的取值范围。

利用数形结合思想分析，设二次函数y=x2+(2k-1)x+(3k+2),题中方程两实根介于2和4之间，即所设函数的图象与x轴的两交点位于（2，0）（4，0）之间。画出满足题意的抛物线的草图（图2）是关键，该图象成立须满足条件如下：(1)△≥0;(2)当x＜2时，y＞0;（3）当x＞4时，y＞0;(4)对称轴应满足。由以上四个条件便可确定k的取值范围。

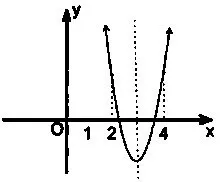
图2

此题运用了二次函数的图象讨论了一元二次方程实根的分布，探求参数的取值范围，其过程渗透了转化思想、函数思想和数形结合的思想。

数形结合的思想，我们还可以通过函数图象得到不等式组、方程组的解集，即函数图象中的交点坐标，利用数形结合，在“形”中找到“数”。在解决一些数学问题时，充分运用数学知识的辅助图形，将数量问题形象化、直观化，使抽象问题一目了然。把问题通过数与形之间的对应关系转化到一个图形去解决，往往能迅速地较为简单地得到解题思路和方法。

在探究中让学生观察图形、猜想、讨论总结，培养学生以“形”助“数”的数学能力。因此，灵活地运用数形结合思想,使本来难解决的问题通过它的“形”，快捷、准确地得到它的“数”，提高了效率。

二、以数助形，图形关系数量化

（一）由形变数，位置关系数量化

由形变数是数形结合思想中一个非常重要的方面。数形结合的思想，可用“数”作为解决“形”的辅助工具，将图形问题数字化。基本图形在初中几何中起着重要的作用，许多基本图形是借助数形结合来解决的。圆的有关位置关系在教学中凸现这一数学思想渗透的案例。

在“直线与圆的位置关系(图3)”这一节课中，我们可以比较圆心o到线的距离d与圆半径r

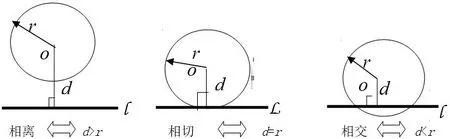
图3

两者的大小,或直线和圆的公共点个数，可确定直线和圆有三种位置关系，相离、相切和相交，得出直线与圆的位置关系的几何特征与种类，进一步深化“数形结合”的数学思想。在探究直线与圆的位置关系时，通过“数”与“形”的结合，形成了用代数法解决几何问题，这种能力使学生以后探究数学问题时，可习惯地使用数形结合的思想解决问题。可见，在图形问题转化为数量问题时，利用代数方法的一般性，解决文题过程的程序化，可操作性强，把有关图形的性质通过数量关系来描述和计算，通过合理简捷的运算解决问题。

（二）以数助形，图形属性精确化

数形结合是一个数学思想方法，它可以借助数的精确性来阐明形的属性，也就是以数作为手段，形作为目的。三国时期吴国的数学家赵爽,创制了一幅“勾股圆方图”,他用几何图形的截、割、拼、补这种动手操作的方法来证明直角三角形三边间的相等关系，利用数形结合思想方法，得出了勾股定理，体现出数形结合的优点。在这幅“勾股圆方图”（图4）中，以弦为边长得到的正方形是由4个全等的直角三角形再加上中间的小正方形组成的。每个直角三角形的面积为,中间的小正方形边长为(b-a),则面积为(b-a)2。于是便可得如下的式子：

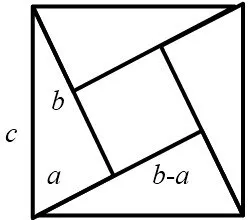
图4

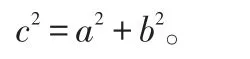
对几何图形的探究，往往需借助于线段或角的数量去分析研究，在探索勾股定理的过程中，正确地引导学生运用数形结合的思想，使他们的思路开阔，方法简便、快捷。说明以“数”助“形”，可使所探究的问题由难变易。

三、数形互化，优势互补，寻求解决问题方案

数形互化指通过数与形之间相互转化来研究并解决问题。在数学教学中，建立数形互化思想并加以运用，寻求解决问题方案，优势互补。初中数学函数主要学习正比例函数、一次函数、反比例函数、及二次函数等内容，函数知识突出的重点与特色就是数学建模与数形结合的思想。

在“二次函数y=a(x-h)2图象及其性质”教学时，利用多媒体演示，观察、比较几个不同的二次函数:。我们可以从不同的角度把两个函数与函数进行对比，得到左右平移的结论。括号内是(x+1)，图象向x轴的负方向平移；括号内是(x-1)，图象向x轴的正方向平移（图5）。通过数的变化得到平移的形，通过形的平移得到变化的数，把这种类型的二次函数写成y=a(x-h)2的形式。当h＞0时，将抛物线y=ax2向右平移h个单位；当h＜0时，将抛物线y=ax2向左平移h个单位。由此可见，数和形互相支撑，可以灵活互化。在初步建立二次函数表达式与图象之间的联系中，从对图形性质的研究而抽象为代数的函数，而对函数图象性质的研究又能发现函数的变化规律，还可以体会到“数”与“形”的互相转化，互相依赖，以及数学的内在美感。

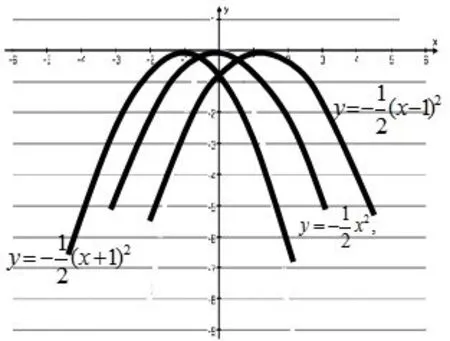
图5

总之，数与形是数学的基本研究对象,它们之间的既对立又统一的关系，揭示了数形结合思想在解决问题时的重要作用,以及数形结合的意义。数形结合是通过图形和数之间的关系，达到数、形互补，从而提高学生的分析问题、解决问题的能力。由于数形结合具有化抽象为形象，直观性强，学生易于接受的优点，我们要把这种数学思想充分渗透到初中数学的各个环节，多渠道向学生传授数形结合的数学思想方法。

(责任编辑：李方满)

廖顺乔，女，广东省高要市金渡镇华侨初级中学，数学中学一级教师。