南海岛礁火力打击作战目标选择模型❋

（海军陆战学院 广州 510430）

1 引言

南海岛礁火力打击作战，是维护国家主权的重要手段，其目的是破坏对方防御体系，为后续登陆作战创造条件。目标选择是火力打击作战筹划和指挥决策的关键问题。当前，目标选择研究没有将备选目标作为一个体系，多是利用专家打分法、综合计算法、排队遴选法、模糊综合评价等孤立地分析目标的重要度［1］，不能体现目标间的信息协同、火力支援等联系。

将目标体系抽象为复杂网络，利用网络描述目标间的联系，是针对目标体系研究目标选择的重要方法。目标选择问题可以借鉴网络抗毁性的研究成果［2～4］，通过逐一去掉节点或边，分析网络在不同攻击策略［5］下的抗毁性，但该方法没有分析同时攻击多个节点或边的网络抗毁性，也没有体现节点的属性，不能直接应用于目标选择问题。文献［6］得到了利用节点介数和节点度确定目标打击顺序的结论，但没有考虑我方作战能力的约束。文献［7］从目标的属性价值和结构价值两个方面，建立目标选择模型，不能反映打击目标和作战效果的关系。

本文考虑双方作战能力和同时打击多个目标的情况，建立能够体现作战效果的南海岛礁火力打击作战目标选择模型。

2 南海岛礁火力打击作战目标选择问题描述

2．1 南海岛礁火力打击作战基本情况

我国南海大量珊瑚岛礁被非法侵占。某国为便于管理和指挥，将岛礁划分为数个“岛礁海区”，同一岛礁海区的岛礁最近仅几海里，成为了一个作战体系，可以进行信息协同、火力支援，作战能力形成了整体。

南海岛礁火力打击作战是利用火力摧毁岛上主要军事设施，降低对方整体作战能力，为后续的登陆作战创造条件。受战场环境和我方作战能力的限制，难以打击全部岛礁。因此，要着眼岛礁防御体系（目标体系）的要害岛礁，巧选一个或数个目标，击破目标体系。

此外，某国在岛礁上严密布防，构筑了大量地下工事，达到了较大岛屿阵地化，较小礁滩堡垒化的要求。因此，对南海岛礁实施火力打击不能完全摧毁岛礁，即岛礁受到打击后仍具有一定的作战能力。

2．2 目标体系网络模型

将同一海区的n个目标（岛礁）抽象为节点，将目标间的协同、支援关系抽象为边，则目标体系可抽象为网络。假定节点集为V＝｛v1，v2，…，vn｝，边集为E＝｛e1，e2，…，em｝⊆V×V，R＝｛r1，r2，…，rn｝为各个目标（节点）作战能力的集合，目标体系的网络模型可表示为图G（V，E，R），图G的邻接矩阵为A＝［aij］。当目标vi和目标vj间存在协同、支援关系，则aij＝aji＝1；否则aij＝aji＝0。

以南沙岛礁群为例，根据岛礁的相对位置及其之间的协同、支援关系，建立南沙岛礁群目标体系的网络模型，如图1所示，序号为节点ID。

图1 南沙岛礁群目标体系网络模型示意图

2．3 目标选择问题实质

将目标体系抽象为网络后，南海岛礁火力打击作战目标选择问题转化为针对节点作战能力和网络拓扑结构，根据我方火力打击能力，选择一个或数个节点实施打击，使目标体系的整体作战能力最小。

3 目标选择模型及算法

3．1 目标体系整体作战能力

目标体系的整体作战能力不简单是各节点作战能力的和，还要考虑由协同、支援产生的“合作能力”。因此，目标体系的整体作战能力包括节点作战能力和“合作能力”两部分［8］。节点间合作的程度可用网络效能表示［9］。网络效能用邻接矩阵的最大特征值表示，如图2所示。

图2 网络示意图及其网络效能

在图2中，由图2（a）、图2（b）可知，相同节点组成不同的网络，具有不同的网络效能；由图2（b）、图2（c）可知，并不是所有的节点都能够形成网络效能，节点6没有改变网络效能。

“合作能力”包括节点两两合作、三三合作等。系统优势函数［8］从线性、非线性两个方面研究节点对整体作战能力的贡献，可以有效地解决“合作能力”的问题。由n个目标构成的目标体系整体作战能力F用系统优势函数表示为

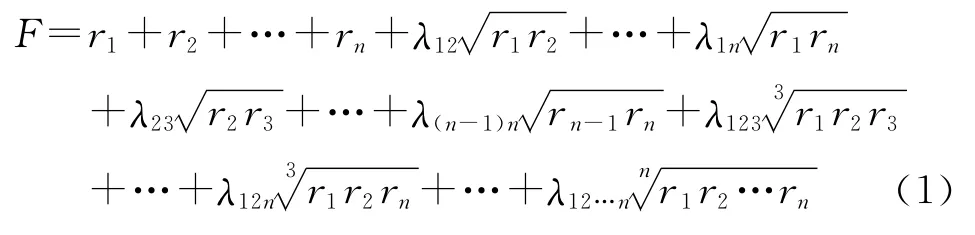
其中，系数λ表示节点间的合作适度性，用相应节点组成的网络的网络效能表示。当考虑节点两两合作时，由于边是无向的，认为两个节点构成一个回路，网络效能为1。

式（1）可表示为

其中，f1＝为线性部分；f2＝为二次非线性部分，是两个节点间直接的信息协同、火力支援的体现；f3＝为三次非线性部分，是三个节点间相互协同、支援的体现，表现为三个节点的情报共享、火力协调；fn＝λ12…n为n个合作产生的合作能力。

3．2 目标选择模型

目标选择是为了使目标体系的整体作战能力最小，因此目标函数为目标体系整体作战能力。定义目标选择向量X＝（x1，x2，…，xn），xi∈｛0，1｝，xi＝1表示选择第i个目标。假定目标遭受打击后作战能力降低60%，则打击后目标体系的整体作战能力为

根据作战原则，我方火力打击能力要大于所选择目标作战能力的和。假定我方火力打击能力为C，利用0-1整数规划［12］，建立目标选择模型为

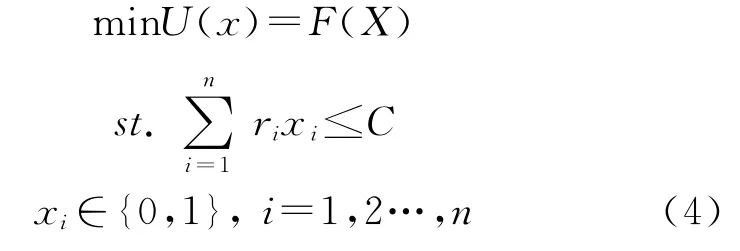
3．3 模型求解算法

目标选择模型求解是一个NP 问题，需用智能优化算法求解。利用约束条件与遗传算法相结合的方法［10］，确定目标选择模型算法流程，如图3所示。

图3 目标选择模型算法流程图

利用遗传算法求解目标选择模型，采用二进制编码方法，将目标选择向量X＝（x1，x2，…，xn）转化为二进制码，编码长度为目标数量n。目标选择模型的解空间为2n，种群规模M取2n。适应度函数为目标函数F（X）。选择操作采用轮盘赌算法，交叉操作采用单点交叉方法，变异操作采用二进制变异，交叉概率Pc和变异概率Pm采用设置—测试的方法确定［11］。终止条件采用规定遗传代数与个体适应度判断相结合的方法，当遗传代数大于某一设定值或适应度函数值变化很小时，则终止搜索，输出最优解。

在交叉、变异后，产生的子代个体必须满足目标选择模型的约束条件，否则要进行修正，随机地将子代个体编码中的1改为0，继续进行约束条件判断。

4 实例分析

我方部分海空兵力对南沙珊瑚岛礁群实施火力打击作战，目标体系的网络模型如图1所示。结合作战实际，根据目标的武器装备战斗力指数及数量，确定目标作战能力集合R＝（49，24，21，109，216，375，233，18）。根据目标体系的网络拓扑结构，计算得到节点间的合作适度性系数λ，如表1所示。

表1 节点间的合作适度性系数

根据式（1），计算得到目标体系打击前的整体作战能力为3220。而各目标作战能力的和为1045，整体作战能力远远大于目标作战能力的和，反映了整体作战能力中的“合作能力”。

假定我方作战能力指数C＝400，利用目标选择模型，求解最优目标选择方案。根据算法流程和目标数量，设定种群规模M＝16，交叉概率Pc＝0．7，变异概率Pm＝0．2，遗传代数为15。利用Matlab编程计算，经过10代遗传，得到最优目标选择方案为（0，1，1，1，1，0，0，1），即 同时打击ID 为2、3、4、5、8的目标。打击后目标体系的整体作战能力为2160，降低了1060。部分目标选择方案对应的目标体系整体作战能力如图4所示。

图4 不同选择方案的目标体系整体作战能力

图4中横坐标为目标选择方案编码的十进制值，实心圆表示最优目标选择方案。由最优目标选择方案可知：火力打击作战没有选择作战能力最强的6号目标，而是通过打击作战能力较弱的目标，降低目标间的“合作能力”，从而最大限度地降低目标体系的整体作战能力。最优目标选择方案体现了“从薄弱环节入手，打击要害目标”的体系作战原则，验证了目标选择模型的合理性和有效性。

5 结语

本文以体系作战思想为指导，针对南海岛礁防御体系的特点，结合火力打击作战实际，建立了一种针对目标体系的目标选择模型。该模型不仅反映了目标间联系对目标选择的影响，而且反映了双方作战能力对目标选择的约束。通过实例分析，验证了模型的合理性和有效性。该模型有效地解决了目标体系的目标选择问题，具有较大的应用价值和军事意义。本文仅对火力摧毁的“硬打击”进行研究，没有考虑利用电子对抗干扰目标间联系的“软对抗”形式，需进一步深入研究。

［1］朱延广，朱一凡．基于影响网络的联合火力打击目标选择方法研究［J］．军事运筹与系统工程，2010，24（3）：64-69．

［2］邓宏钟，吴俊，李勇，等．复杂网络拓扑结构对系统抗毁性影响研究［J］．系统工程与电子技术，2008，30（12）：2425-2428．

［3］Albert R，Jeong H，Barabasi A-L．Attack and Error Tolerance of Complex Networks［J］．Nature，2000，406：378-382．

［4］狄鹏，胡涛，胡斌，等．基于复杂网络的作战网络模型抗毁性研究［J］．系统仿真学报，2011，23（1）：56-60．

［5］黄仁全，李为民，董雯，等．不同攻击策略下作战体系网络抗毁性研究［J］．复杂系统与复杂性科学，2012，9（3）：62-69．

［6］阮树鹏，赵文杰，雷盼飞，等．基于复杂网络的防空武器系统目标选择研究［J］．指挥控制与仿真，2012，34（1）：23-28．

［7］贾子英，刘新科，王海生．空中力量体系对抗中目标选择方法［J］．海军航空工程学院学报，2012，27（4）：477-480．

［8］贾子英，闫飞龙，王海生．网络化效能的防空体系作战效能评估［J］．火力与指挥控制，2013，38（5）：82-85．

［9］Jeff Cares．Distributed Networked Operations-The Foundations of Network Centric Warfare［M］．New-York：Alidade Press，2006：65-68．

［10］王中杰，李侠，周启明，等．基于多约束条件遗传算法的雷达网优化部署［J］．系统工程与电子技术，2008，30（2）：265-268．

［11］刘大莲，徐尚文．求解约束优化问题的内外交叉遗传算法［J］．系统工程理论与实践，2012，32（1）：189-195．

［12］李忠明，刘伟，焦宗夏．整数规划的旋转矢量法［J］．系统工程与电子技术，2012，34（5）：1058-1061．