表贴式永磁同步电动机永磁体气隙磁场解析计算＊

刘 珂 让余奇

（海军工程大学 武汉 430033）

1 引言

永磁同步电动机以永磁体提供的磁通替代电励磁同步电动机的由励磁绕组提供机电能量转换所需要的磁场，具有结构简单、体积小、重量轻、效率高的特点。永磁体的结构设计是永磁同步电动机优化设计的重要方面，而电机内气隙磁场分布的准确计算是电机优化设计和性能分析的必要过程。解析方法可以较准确地计算气隙磁场分布波形，同时可以观察到气隙磁场分布于结构尺寸之间的关系［1～4］，具有很强的实用性。本文针对表贴式永磁同步电动机，利用等效面电流法推导出了永磁同步电动机永磁体在径向充磁和平行充磁两种充磁方式下的气隙磁密的解析计算公式。通过比较不同永磁体结构在上述两种充磁方式下产生的气隙磁场，给出了一种偏心不等半径瓦片形磁极结构来改善气隙磁场，使得气隙磁场的波形更好，从而降低电机的振动和噪声。同时解析计算易于与计算机结合应用，计算时间短，为永磁同步电动机的优化设计提供了基本的分析手段。

2 永磁同步电动机永磁体的数学模型

应用解析法对永磁同步电动机电磁场进行分析时，一般采用以下一些假设［5］：

1）电机的定转子铁心的磁导率为无穷大；

2）忽略电机的端部影响；

3）永磁体退磁曲线为直线，永磁体为均匀磁化；

4）电枢表面光滑，开槽用等效气隙考虑。

在处理永磁体励磁作用时做了以下两点假设：

1）设永磁体的磁导率与空气的磁导率相同，即相对回复磁导率μr＝1；

2）永磁体极性交替分布，呈现出一定的周期性，但是极间还是断开的。假设永磁体极间部分也全部由永磁体充满，只是极间永磁段未被磁化。

3 永磁体的等效面电流法

电流与磁场的基本关系表明，任何磁场都可以认为是由分布电流产生的。面电流法在永磁体边界上模拟电流的存在，如果永磁体被均匀磁化，则永磁体内部等效体电流密度为零，在平行于磁化方向的永磁体边界上，存在一层等效面电流。如图1所示，三角形为一个永磁体单元。

图1（a）假设永磁体的磁化方向垂直于边ij，则在边ij上无电流，在边jm和mi上的电流为

图1（b）假设永磁体的磁化方向是任意的，磁化方向与x轴的夹角为θn，则三条边上对应的等效电流分别为

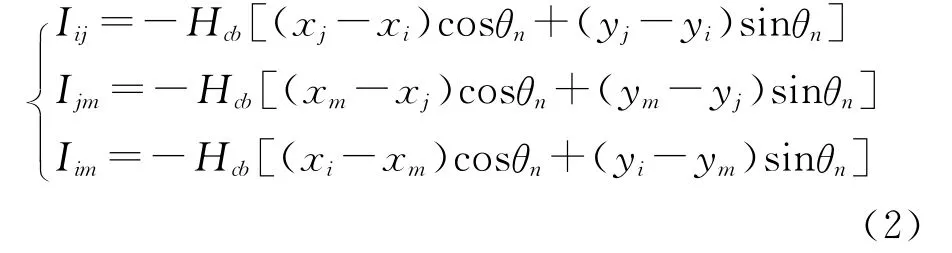
图1 永磁体单元磁化图

在永磁体内部（永磁边界上的单元边除外），任何一条边都被两个三角形单元共有，两个单元在该边上的等效电流符号相反、大小相同，那么就互相抵消。因为对两个单元来讲，磁化方向相同，但l矢量的方向相反（单元逆时针方向编号），因此只有永磁边界上才存在等效电流［6］。

4 永磁体产生的气隙磁场解析计算

在表贴式永磁同步电动机中，瓦片形磁极应用最广泛，瓦片形磁极有平行充磁和径向充磁两种充磁方式［7］。

1）径向充磁同圆心不同半径瓦片形永磁产生的气隙磁密

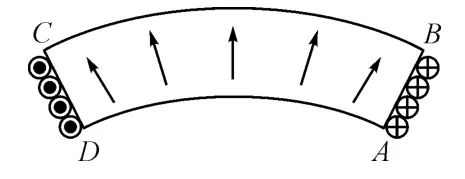
图2 径向充磁时的面电流等效

根据面电流法，同心圆径向充磁永磁体等效面电流如图2所示，AD和BC边垂直于充磁方向，面电流密度大小等于零；AB和CD边平行于充磁方向，面电流密度大小等于永磁体矫顽力。

设一个径向充磁的永磁体磁极等效线圈的径向面电流微元为di，径向长度微元为dr，永磁体的矫顽力为Hcb，于是AB和CD边的等效面电流微元为

由式（3）可得到永磁体表面等效的电流微元di在气隙所产生的磁密为

对上式积分可以得到在气隙圆周定子内表面产生的磁密为

式中：α为瓦片形永磁体AB边到中心线的机械角；θ为气隙圆周上某一点到中心线的机械角；hm为永磁体径向长度；Rs为定子内半径，Rr为转子外半径；P为永磁体极对数；Kym＝sinmα为m 次谐波的节距因数。

多极永磁同步电动机中永磁体依次放置在转子圆周表面，那么其它永磁磁极产生的气隙磁密可采用类似的方法进行计算，只是沿定子内径表面的角度不同，然后只用对每个永磁磁极所产生的磁密进行累加即可。

设有2P个径向充磁的永磁体放置于转子表面，且极性交叉放置，则第l个永磁磁极在定子内表面产生的磁密为

可得2P个磁极在定子内表面产生的磁密为

上述公式都是在假设永磁电机定子和转子表面光滑时得到的，但是现代永磁电机的定、转子铁芯一般都有不同程度的开槽，电枢绕组嵌放在开槽的电枢铁心里，开槽一方面改变气隙磁场的分布，另一方面使气隙磁阻增大。在磁场计算时，通常把开槽的影响作为有效气隙放大来考虑。本文只考虑定子侧开槽影响，此时用卡氏系数kc进行修正，使有效气隙放大，即δ′＝kcδ。其中卡氏系数的计算式为［8～10］

式中，τ为槽距，δ为气隙长度，b0为槽口宽。

图3 径向充磁同心不同半径气隙磁密

下面给出一永磁电机气隙磁密解析计算结果，该电机相关参数为：转子外半径Rr＝89.8mm，定子内半径Rs＝105mm，极对数P＝2，永磁体厚度hm＝12mm，永磁体张角2α＝90°，矫顽力 Hcb＝920550A／m，槽距τ＝13.74mm，槽口宽b0＝4mm。其解析计算结果如图3所示。

2）平行充磁同圆心不同半径瓦片形永磁产生的气隙磁密

由于制作工艺的限制，标准的径向充磁很难达到；实际应用中，平行充磁永磁体的工艺简单易行，因此分析平行充磁永磁体产生的气隙磁场更具实用性［11］。

平行充磁时磁化方向平行于瓦片形永磁体的中心线，其磁化方向和永磁体各边等效面电流方向如图4所示。

图4 平行充磁永磁体面电流等效

由面电流法，沿永磁体表面AB与CD的电流层方向相反，大小相同，其面电流密度大小为

沿AD和BC边变化的面电流密度的大小为

那么平行充磁同心瓦片形永磁体AB＿CD段面电流产生的气隙磁密为

BC段面电流产生的气隙磁密为

其中，b＝Rr＋hm。

AD段面电流产生的磁密：

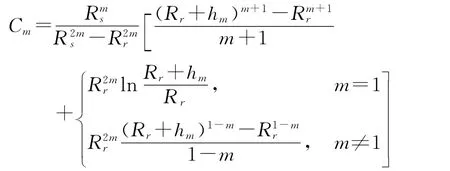
一个平行充磁的永磁体在定子内表面产生的磁密B1（θ）为AB、CD、BC和AD 各段的叠加，即：

与径向充磁时多极永磁体磁密计算类似，则平行充磁时2P个磁极的AB、CD、AD、BC各段在定子内表面产生的磁密为

式（15）中A、Cm、Kym和式（11）相同。

上式中A、Cm和式（12）相同。

上式中A、Cm和式（13）相同。

于是多极平行充磁瓦片形永磁体在定子内表面产生的磁密为

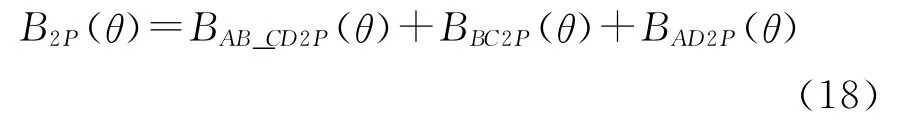
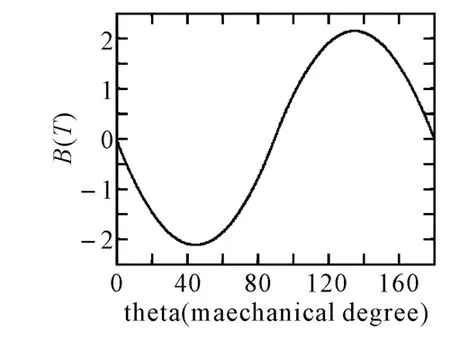
图5 平行充磁同心不同半径气隙磁密

下面给出一永磁同步电动机气隙磁密解析计算结果，该电机相关参数为转子外半径Rr＝28mm，定子内半径Rs＝36mm，极对数P＝1，永磁体厚度hm＝6.5mm，永磁体张角2α＝180°，矫顽力 Hcb＝935000A／m，槽距τ＝12.56mm，槽口宽b0＝2.5mm。其解析计算结果如图5所示。

3）平行充磁不同圆心不同半径瓦片形永磁体产生的磁密

为了满足在平行充磁条件下获得理想的磁密波形的要求，本文给出了一种偏心不等半径瓦片形磁极结构。下面对其产生的气隙磁密进行分析推导。一个极下的永磁体尺寸如图6所示，其永磁体的面电流等效与图4一致。

图6 不同圆心不同半径永磁体尺寸

在已知最小气隙长度δmin，最大气隙长度δmax，定子内半径Rs，转子外半径Rr，永磁体张角2α，永磁体矫顽力Hcb前提下，可计算与气隙磁场有关的参数。

永磁体AB边和CD边的圆心距为

永磁体上以O′为圆心，BC为边的圆弧半径为

永磁体BC边上某一点E与O点对应的角度为θ0，那么与O′点对应的角度为θ′0，即：

E点到O点的距离R（θ0）为

沿AB和CD 边的面电流密度大小为式（9），沿AD边的面电流密度大小为式（10），沿BC边的面电流密度的大小为

式中，θ′0为BC上某一点到中心线的机械角。

BC边的等效面电流微元为

该电流微元产生的磁密为

由上可得BC边的磁密为

上式不能直接给出磁密的解析表达式，需用数值积分的方法求解。多极时，处理方法同1）、2）中的相关介绍。

AB、CD、AD边上等效面电流产生的磁密解析计算公式分别和式（15）、式（16）一样。

图7 平行充磁不同心不同半径时气隙磁密

算例分析：永磁同步电动机电机中，最小气隙长度δmin＝3.2mm，最大气隙长度δmax＝5.5mm，定子内半径Rs＝105mm，转子外半径Rr＝89.8mm，永磁体张角2α＝90°，永磁体矫顽力 Hcb＝920550A／m，计算得到的圆心距H＝8.4mm，BC边的圆弧半径为Rm＝107.9mm。其解析计算结果如图7所示。

由图7可知，通过调整最大、最小气隙的数值，可以使得平行充磁磁极的气隙磁密波形平顶部分很平直，并且可以获得所需要的波宽。同时，我们可以改变永磁体的形状或者几种不同形状的永磁体混合，使电机的气隙磁密达到我们需要的波形，例如不同平顶宽度的梯形波磁密、正弦波磁密等。

5 结语

本文根据等效面电流法推导了表贴式永磁同步电动机永磁体气隙磁场在径向充磁和平行充磁两种充磁方式下的解析计算公式；通过对两种充磁方式下不同磁极结构的对比分析，本文给出了一种偏心不等半径瓦片形磁极结构，可以使得气隙磁场的波形更好，从而降低电机的振动和噪声；同时，解析计算可以便捷地得到永磁同步电动机的气隙磁场分布波形，为永磁同步电动机的优化设计提供了基本的分析手段。

［1］唐任远.现代永磁电机理论与设计［M］.北京：机械工业出版社，2006：3－260.

［2］诸自强，D.豪，E.波尔特，等.永磁无刷直流电机瞬态磁场分布，Ⅰ部分：磁场开路［J］.美国电气电子工程师协会电磁场汇刊，1993，29（1）：124－135.

［3］王兴华，励庆孚，王曙鸿.永磁无刷直流电机负载磁场及其电磁转矩的计算［J］.中国电机工程学报，2003，23（4）：140－144.

［4］陈阳生，林友仰.永磁电机气隙磁密的分析计算［J］.中国电机工程学报，1994，14（5）：17－26.

［5］汤蕴璆.电机内的电磁场［M］.第二版.北京：北京科学出版社，1998：155－156.

［6］王秀和.永磁电机［M］.北京：中国电力出版社，2007：61－64.

［7］陈世坤.电机设计［M］.北京：机械工业出版社，2004：51－52.

［8］王兴华，励庆孚，王曙鸿.永磁无刷直流电机空载气隙磁场和绕组反电势的解析计算［J］.中国电机工程学报，2003，23（3）：126－130.

［9］潘元璋.高功质比永磁同步电动机电磁振动与噪声研究［D］.武汉：海军工程大学，2012：33－36.

［10］于慎波.永磁同步电动机振动与噪声特性研究［D］.沈阳：沈阳工业大学，2006：72－77.

［11］李俊武.小功率永磁同步电动机电磁振动与噪声研究［D］.哈尔滨：哈尔滨工业大学，2009：46－47.