层理页岩水平井井周剪切失稳区域预测方法
2014-11-27马天寿
马天寿,陈 平
(油气藏地质及开发工程国家重点实验室(西南石油大学),四川成都610500)
长宁-威远、昭通、重庆涪陵等地区的页岩气水平井钻探试采结果表明,页岩气水平井钻井过程中井眼垮塌十分严重,卡钻、埋钻等井下故障频发[1-3],严重影响了页岩气水平井的钻井周期、固井完井质量和压裂施工效果,井壁失稳严重时甚至导致井眼报废,造成巨大的经济损失,直接影响到了页岩气开发效果。页岩气水平井井眼坍塌失稳已经成为制约页岩气长水平段水平井钻井的主要技术瓶颈[3-4]。
页岩气储层的层理、微裂隙十分发育,导致页岩强度存在显著的各向异性特征,国内外学者也开展了大量研究。B.S.Aadn∅y[5]针对强度各向异性地层开展井壁稳定研究,基于线弹性力学理论和Mohr-Coulomb弱面强度准则,研究了地层强度各向异性对井壁稳定的影响,但没有考虑孔隙压力等因素的作用。此后,国外的 M.B.Dusseault[6]、S.H.Ong[7]、D.Okland[8]、T.M.Al-Bazali[9]、H.Lee[10]等人和国内的金衍[11]、刘 向 君[12]、袁 俊 亮[13]、Lu Yunhu[14]、刘 志远[15-16]、温航[17]等人在 B.S.Aadnoy模型的基础上,考虑弹性各向异性、孔隙压力、渗透性和化学等因素的影响,对页岩井壁稳定进行了进一步的研究。但是,以上研究在计算时仅考虑了井壁处的应力及破坏,没有对井周地层在层理等弱面影响下破坏失稳区域的特征进行研究。为此,笔者研究了页岩强度各向异性特征,结合井周地层弹性应力分布模型及含弱面页岩剪切破坏准则,分析了钻进方位对井周失稳区域的影响,以揭示层理等弱面影响下井周地层坍塌失稳的规律及机理。
1 页岩的强度各向异性特征
页岩气储层的层理、微裂隙十分发育,存在显著的强度各向异性特征。M.E.Chenevert等人[18]通过试验研究了层理对岩石力学特性的影响,结果表明,当岩心轴线与层理夹角为20°~30°时,其强度比垂直层理的强度低40%左右。为了进一步明确页岩强度各向异性特征,取四川南部长宁双河地区龙马溪组露头,制取50mm×50mm×50mm岩样,采用岩石直剪仪进行了沿层理(弱面)和垂直层理(本体)的直剪试验,结果如图1所示。

图1 页岩直剪试验结果Fig.1 Direct shear test data of shale
为了与典型页岩强度各向异性特征进行对比,选用文献[19]中的数据和试验数据进行对比分析(见表1),采用相关系数拟合方法对表1中的内聚力和内摩擦角进行拟合,拟合结果如图2和图3所示。

表1 页岩强度各向异性数据对比Table 1 Strength anisotropy data of shale
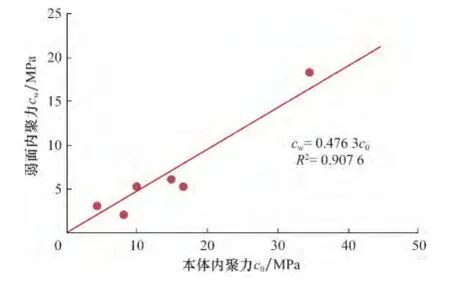
图2 页岩本体内聚力与弱面内聚力的相关性Fig.2 Cohesion correlation between weak plane and rock mass
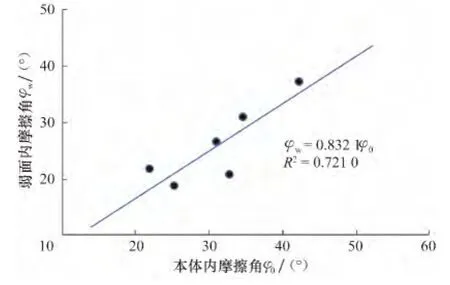
图3 页岩本体内摩擦角与弱面内摩擦角的相关性Fig.3 Correlation of internal frictional angle of weak plane and rock mass
从图2和图3可以看出:1)页岩弱面与本体强度参数基本呈线性关系,cw=0.476 3c0,φw=0.832 1φ0,本体内聚力大约为弱面的2.10倍,而本体内摩擦角大约为弱面的1.20倍;2)由单轴强度来看,Pedernales页岩本体与弱面强度的差异最大(4.32倍),其次是川南龙马溪组页岩(3.99倍),再次分别是Tournemire、Permian、Trafalgar和 Pierre 1页岩;3)龙马溪组页岩本体内聚力和弱面内聚力的比值为3.06,内摩擦角比值为1.57,若采用 Mohr-Coulomb准则换算成三轴抗压强度,30MPa围压下的抗压强度比值为2.06,60MPa围压下的抗压强度比值为1.85,90MPa围压下的抗压强度比值为1.78,说明龙马溪组页岩强度各向异性特征十分显著。
2 井周弹性应力分布模型
2.1 井周应力坐标转换关系
假设大地全局坐标系(global coordinate system,GCS)为(N,E,Z),井眼直角坐标系(borehole coordinate system,BCS)为(xb,yb,zb),井眼圆柱坐标系(cylindrical coordinate system,CCS)为(r,θ,zb),层理等弱面的直角坐标系(weak-plane coordinate system,WCS)为(xw,yw,zw)(见图4)。其中,原地应力(σH、σh、σv)采用最大水平主应力方位角Ω描述其在GCS中的空间关系;BCS与GCS的关系采用井斜角α和井斜方位角ψ描述;CCS与BCS的关系采用井周角θ描述;WCS与GCS的关系采用弱面倾角φ和弱面倾斜走向γ描述。
原地应力(σH、σh、σv)与大地全局坐标 GCS的转换关系为:

井眼直角坐标BCS与大地全局坐标GCS的转换关系为:

井眼圆柱坐标CCS与井眼直角坐标BCS的转换关系为:

弱面直角坐标WCS与大地全局坐标GCS的转换关系为:

图4 井周应力转换坐标关系Fig.4 Coordination transformation for stress around borehole
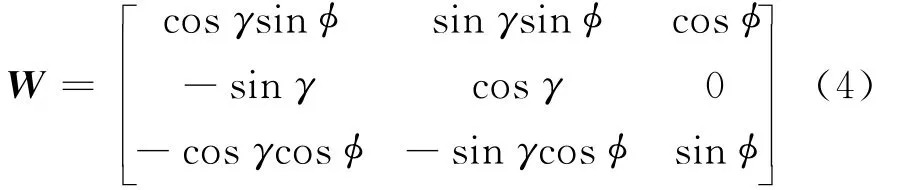
式中:Ω为最大水平主应力在GCS中的方位角,(°);α为井斜角,(°);ψ为井斜方位角,(°);θ为井周角,(°);φ为弱面倾角,(°);γ为弱面倾斜走向方位角,(°);E、B、C、W为坐标转换矩阵。
2.2 井周应力状态弹性解
Bradely[11]给出了斜井井周应力分布的弹性解:

其中

而原地应力(σH,σh,σv)在BCS中的井周远场应力张量σin-situ-BCS由如下坐标转换关系得到:
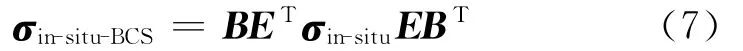
其中

通过上述方法求得的井周应力分量写成CCS中的应力张量:
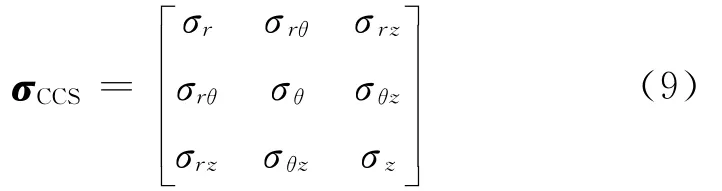
式中:σr,σθ,σz,τrθ,τrz和τθz为井周有效应力分量,MPa;σxx,σyy,σzz,σxy,σxz和σyz为原地应力转换至BCS下的应力分量,MPa;σH,σh和σv为原地应力,MPa;rw为井眼半径,m;r为井周地层径向距离,m;αp为Biot弹性系数,一般取1;υ为泊松比;pm为井筒钻井液压力,MPa;pp为地层孔隙压力,MPa;σin-situ-BCS为BCS坐标系中的井周远场应力张量,MPa;σin-situ为GCS坐标系中的原地应力张量,MPa;σCCS为CCS坐标系中的井周应力张量,MPa。
3 井周地层剪切破坏准则
3.1 Mohr-Coulomb弱面强度理论
Jaeger等人[20]对层状岩体弹性参数各向异性的试验结果和理论进行分析,建立了横观各向同性岩体的破坏准则,描述了具有一条或一组平行弱面各向同性岩体的剪切破坏,由于这是对Mohr-Coulomb准则的推广,称为Mohr-Coulomb弱面强度理论。
岩体中发育一组弱面AB,假定AB面(法线)与最大水平主应力方向夹角为β(见图5)。

图5 Mohr-Coulomb弱面强度理论关系Fig.5 Mohr-Coulomb weak plane strength theory
根据Mohr应力圆理论和Coulomb准则,沿弱面剪切滑移的破坏准则为:
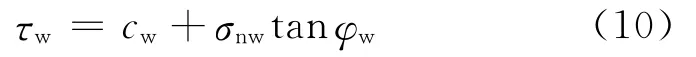
式中:τw为弱面上的最大剪应力,MPa;σnw为弱面上的法向应力,MPa;cw为弱面内聚力,MPa;φw为弱面内摩擦角,(°)。
为了对弱面的强度进行判别,可以将CCS中的应力张量转换至WCS坐标[19],其转换关系为:

其中

则弱面上的法向应力和最大剪应力[19]为:
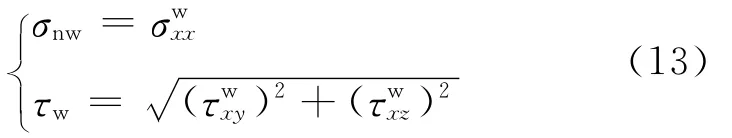
式中:σCCS-WCS为 WCS坐标系中的应力张量,MPa;σnw为弱面上的法向应力,MPa;τw为弱面上的最大剪应力,MPa。
岩体沿弱面剪切滑移的破坏准则可改写,并据此定义一个判别井周岩石剪切破坏的指数,附加内聚力指数cwf,其表达式为:

式中:cwf为弱面附加内聚力指数,MPa和为WCS中的应力分量,MPa。
从式(14)可以看出,cwf指的是弱面上的剪应力超过弱面本身能够承受的最大剪切力的数值,即维持弱面稳定所需的附加内聚力数值,cwf越大则井眼稳定性越差,cwf越小则井眼越稳定。
3.2 Mohr-Coulomb准则
若不考虑弱面强度对井眼稳定的影响,一般可以采用 Mohr-Coulomb准则进行判别,Mohr-Coulomb准则认为[20]:岩石的强度等于岩石本身抗剪切摩擦的粘结力和剪切面上法向力产生的摩擦力,即:

式中:τ0为剪应力,MPa;σn0为法向应力,MPa;c0为岩石内聚力,MPa;φ0为岩石内摩擦角,(°)。
为了便于计算,将Mohr-Coulomb准则改写成最大主应力和最小主应力表达的形式:
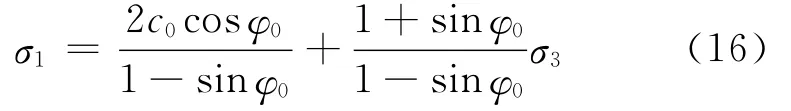
式中:σ1为最大主应力,MPa;σ3为最小主应力,MPa。
而井眼圆柱坐标系CCS中的最大、最小主应力为:

其中

式中:I1为应力张量的第一不变量;J2为应力偏量的第二不变量;J3为应力偏量的第三不变量。
为了与弱面强度准则判别形成对比,定义附加内聚力指数c0f,判别井周岩石的剪切破坏情况,其表达式为:

式中:c0f为岩石本体附加内聚力指数,MPa。
从式(19)可以看出,c0f指的是岩石本体上的剪应力超过岩石本身能够承受的最大剪切力的数值,即维持井周页岩稳定所需的附加内聚力数值,c0f越大井眼稳定性越差,c0f越小井眼越稳定。
4 井周地层剪切失稳区域分布规律
为了分析井周地层在层理等弱面影响下破坏失稳区域的特征,采用Matlab软件编制了计算程序,并根据页岩地层基础参数(见表2)进行分析,其中岩石强度参数取上文试验结果。考虑到目前页岩气水平井井斜角一般为80°~100°,同时考虑层理影响和不考虑层理影响2种情况,分别计算了沿0°、90°、75°、165°和345°不同方位钻进井斜角为80°~100°井眼时井周地层剪切破坏的附加内聚力指数分布情况。

表2 页岩地层基础参数Table 2 Basic parameters of shale formation
4.1 沿最大水平主应力方向钻进
沿最大水平主应力方向0°钻进水平井时的计算结果如图6所示。为了直观地表达计算结果,图中井径采用井眼半径的无因次长度表示,并以井斜横截面方式表达井周地层剪切破坏失稳区域(其坐标关系见图4(c),图中深蓝色区域为稳定区域,彩色区域为剪切破坏失稳区域)。从图6可以看出,存在以下3种情况:井周地层在井眼横截面方向线两端靠近井壁位置发生本体剪切破坏,坍塌失稳区域呈对称分布(见图6(a));井周地层发生层理面剪切滑移破坏的位置在井眼横截面方向线两端的上下侧,形成4个(2对轴对称)不对称的坍塌区域,其中一对失稳区域向井眼高边和低边偏转大约40°,另一个失稳区域向井眼高边和低边偏转大约10°(见图6(b));井眼失稳区域是图6(a)和图6(b)的并集,实际井眼的坍塌深度和宽度主要受弱面控制,井眼崩落宽度达112°,扩径率约25%,说明沿0°方向钻进井眼稳定性较差(见图6(c))。另外,随着井斜角增大,井眼稳定性变好,井斜角80°井眼最不稳定,但整体变化幅度不大。
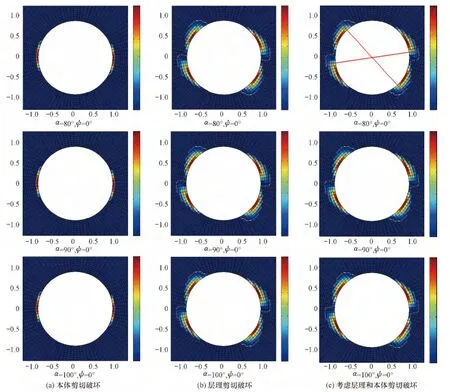
图6 0°方向水平井井周剪切破坏区域分布Fig.6 Distribution of shear failure regions around horizontal borehole in 0°direction
计算结果表明,考虑层理和本体剪切破坏计算得到的井周地层失稳区域形状并非传统的“狗耳朵”形状。D.Okland等人[8]采用与井下岩样性质相似的露头岩样进行了厚壁圆筒测试,发现层理与厚壁圆筒轴向夹角对井眼稳定影响较大:当厚壁圆筒轴向垂直于层理时,井眼相对稳定;当厚壁圆筒轴向平行于层理时,井眼十分不稳定,此时将形成比“狗耳朵”形状更大、更复杂的崩落区域,该崩落区域呈轴对称分布,垮塌后的井眼形状类似于方形(见图7(a))。这与 Li Yufei等人[1]的计算结果(见图 7(b))基本吻合。造成这种现象的原因是:1)井周地层沿层理等弱面剪切滑动;2)钻井液侵入导致流体渗入及压力增加,从而造成垮塌;3)存在多个层面,造成碎裂而崩落,如层理面、节理和裂缝等;4)破碎性地层井眼高边在重力作用下垮塌。
4.2 沿最小水平主应力方向钻进
沿最小水平主应力方向90°钻进水平井时的计算结果如图8所示。从图8可以看出,存在以下3种情况:井周地层不会发生本体剪切破坏(见图8(a));井周地层发生层理面剪切滑移破坏的位置仍然在井眼横截面方向线两端的上下侧,形成4个(2对轴对称)不对称的坍塌区域,其中一对失稳区域向井眼高边和低边偏转大约50°,另一对失稳区域向井眼高边和低边偏转大约25°(见图8(b));实际井眼的坍塌深度和宽度完全受弱面控制,井眼崩落宽度达108°,扩径率大约15%(见图8(c))。另外,随着井斜角增大,井眼稳定性先变差后略微变好,即井斜角90°井眼最不稳定,但整体变化幅度不大。

图7 井周失稳区域形状Fig.7 Shape of shear instability region around a borehole

图8 90°方向水平井井周剪切破坏区域分布Fig.8 Distribution of shear failure regions around horizontal borehole in 90°direction
4.3 沿层理面走向方向钻进
沿层理走向方向75°钻进水平井时的计算结果如图9所示。从图9可以看出,存在以下3种情况:井周地层不会发生本体剪切破坏(见图9(a));井周地层发生层理面剪切滑移破坏的位置仍然在井眼横截面方向线两端的上下侧,形成4个(2对轴对称)不对称的坍塌区域,其中一对失稳区域向井眼高边和低边偏转大约48°,另一对失稳区域向井眼高边和低边偏转大约25°(见图9(b));实际井眼的坍塌深度和宽度完全受弱面控制,井眼崩落宽度达116°,扩径率大约20%(见图9(c))。另外,随着井斜角增大,井眼稳定性先变差后略微变好,即井斜角90°井眼最不稳定,但整体变化幅度不大。

图9 75°方向水平井井周剪切破坏区域分布Fig.9 Distribution of shear failure regions around horizontal borehole in 75°direction
4.4 沿层理面上倾方向钻进
沿层理上倾165°方向钻进水平井时的计算结果如图10所示。从图10可以看出,存在以下3种情况:井周地层在井眼横截面方向线两端靠近井壁位置发生本体剪切破坏,坍塌失稳区域呈对称分布(见图10(a));井周地层发生层理面剪切滑移破坏的位置在井眼横截面方向线两端的上下侧,形成4个(2对轴对称)不对称的坍塌区域,其中一对失稳区域向井眼高边和低边偏转大约45°,另一个失稳区域向井眼高边和低边偏转大约20°(见图10(b));井眼失稳区域是图10(a)和图10(b)的并集,实际井眼的坍塌深度和宽度主要受弱面控制,井眼崩落宽度达116°,扩径率约30%,说明沿层理上倾165°方向钻进井眼稳定性较差(见图10(c))。另外,随着井斜角增大,井眼稳定性变差,即井斜角100°井眼最不稳定,这主要是由于沿着层理上倾165°方向钻进井斜角100°井眼时,井眼轴线与地层层面呈3°夹角,且受地应力方向影响,井眼稳定性比较差;若井眼井斜角为97°时,井眼沿着地层层面钻进,此时井眼最不稳定。
4.5 沿层理面下倾方向钻进
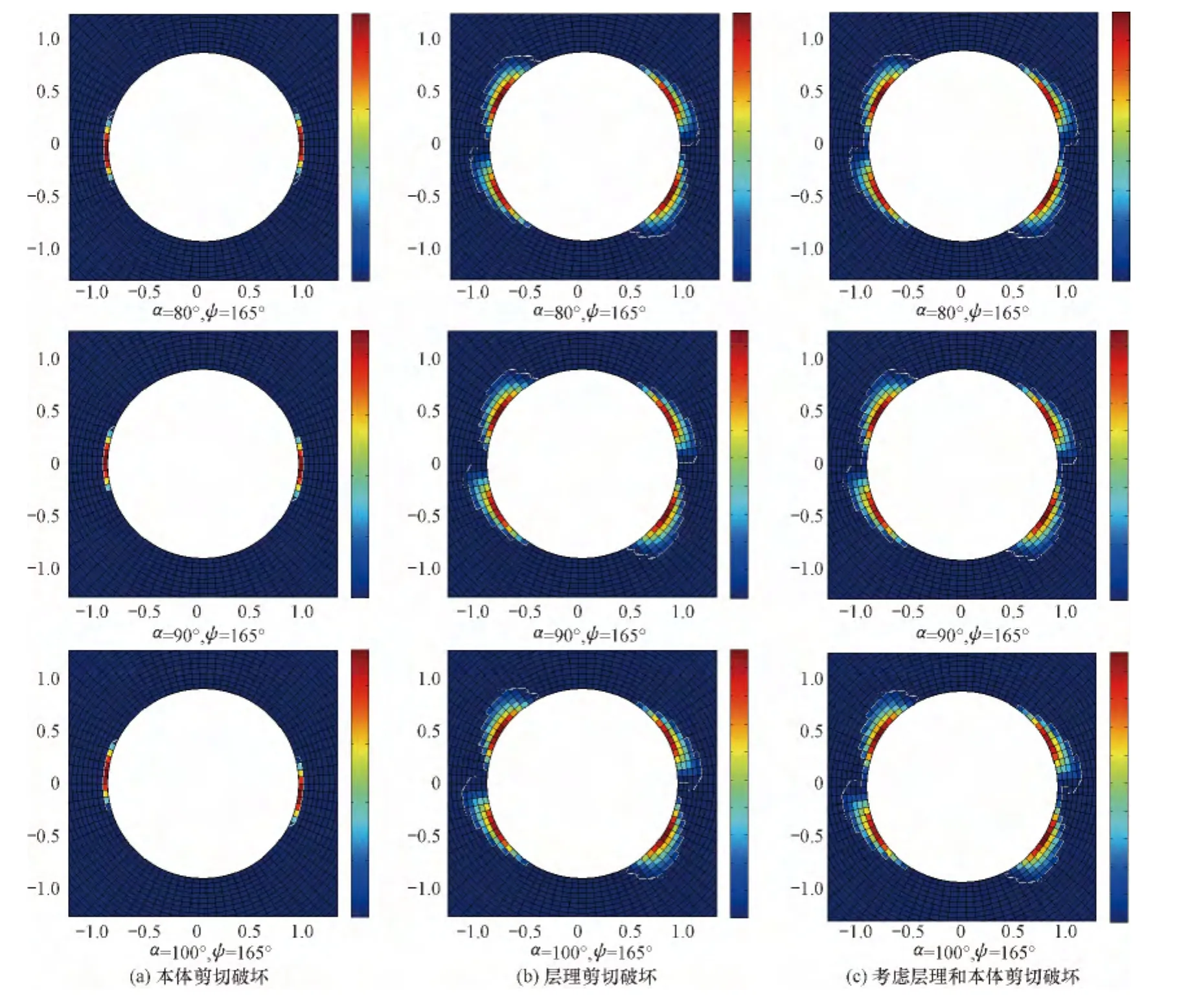
图10 165°方向水平井井周剪切破坏区域分布Fig.10 Distribution of shear failure regions around horizontal borehole in 165°direction
沿层理下倾345°方向钻进水平井时的计算结果如图11所示。从图11可以看出,存在以下3种情况:井周地层在井眼横截面方向线两端靠近井壁位置发生本体剪切破坏,坍塌失稳区域呈对称分布(见图11(a));井周地层发生层理面剪切滑移破坏的位置在井眼横截面方向线两端的上下侧,形成4个(2对轴对称)不对称的坍塌区域,其中一对失稳区域向井眼高边和低边偏转大约45°,另一个失稳区域向井眼高边和低边偏转大约15°(见图11(b));井眼失稳区域是图11(a)和图11(b)的并集,实际井眼的坍塌深度和宽度主要受弱面控制,井眼崩落宽度达120°,扩径率大约30%,这说明沿层理下倾345°方向钻进井眼稳定性也比较差(见图11(c))。另外,随着井斜角增大,井眼稳定性变好,即井斜角80°井眼最不稳定,这主要是由于沿层理下倾345°方向钻进井斜角80°井眼时,井眼轴线与地层层面夹角呈3°,且受地应力方向影响,井眼稳定性比较差;若井眼井斜角为83°时,井眼沿着地层层面钻进,此时井眼最不稳定。
5 实例分析
川南长宁-威远页岩气示范区某井页岩气储层为志留系龙马溪组,该井设计井深4 239m(垂深2 485m),设计靶前距600m,水平段长1 200m。该井基础地质力学参数和地层强度参数见表2,另外,最大水平主应力方位NE115°,层理倾角7°,层理走向NE132°,分别分析不考虑层理和考虑层理影响下的坍塌压力当量密度分布规律,分析结果如图12所示。

图11 345°方向水平井井周剪切破坏区域分布Fig.11 Distribution of shear failure regions around horizontal borehole in 345°direction
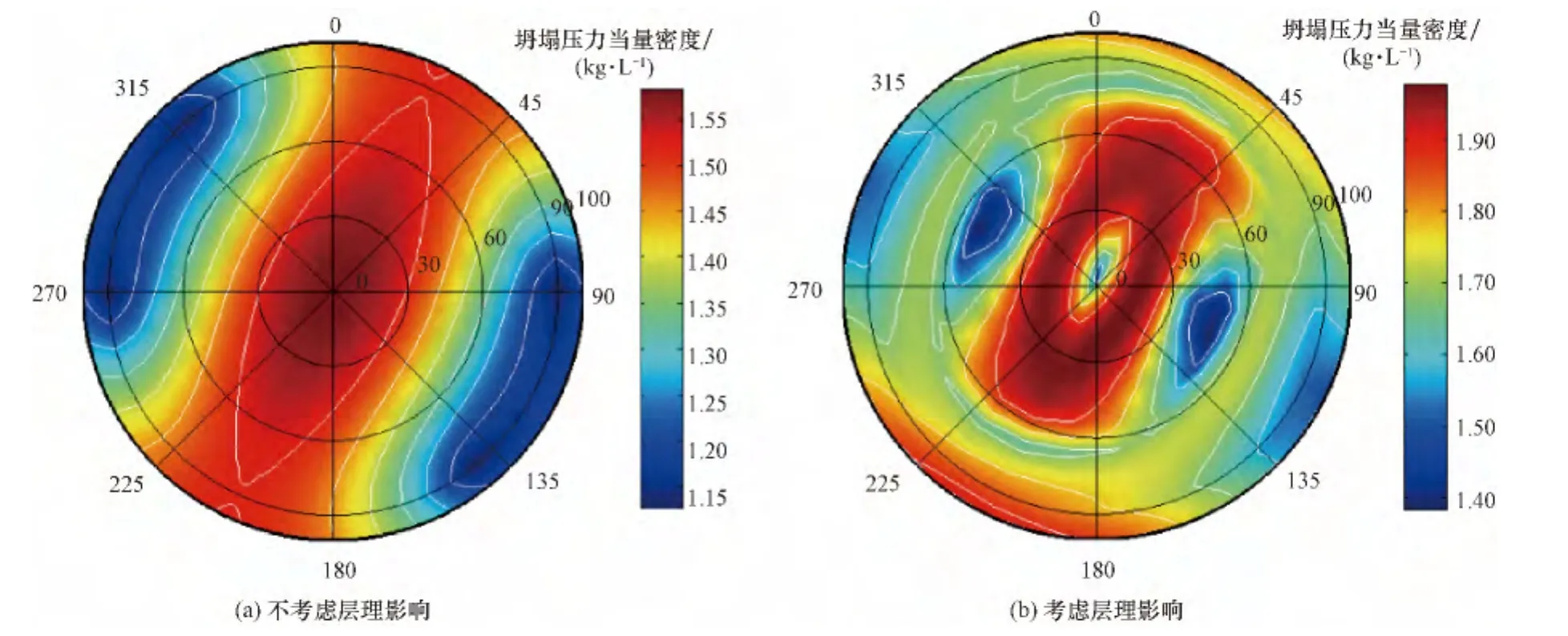
图12 页岩井眼坍塌压力当量密度分布规律Fig.12 Distribution pattern of equivalent density of collapse pressure for shale wells
该井水平段沿着最小水平主应力方向钻进,钻进方位角为NE25°,水平段井斜角96°,采用了密度1.84kg/L的合成基钻井液,不考虑层理影响,计算出维持井眼稳定所需钻井液密度为1.50kg/L(见图12(a)),考虑层理影响计算出维持井眼稳定所需钻井液密度为1.82kg/L(图12(b)),说明弱面的存在将使井眼坍塌的风险显著增大。尽管实际采用的钻井液密度略大于计算结果,但是,该井水平段着陆后,在页岩水平段(2 700~2 900m)钻进中发生垮塌,因为对页岩垮塌及“上翘”井眼岩屑床的认识不足造成卡钻,卡钻井深3 066.60m(垂深2 486m)。垮塌掉块岩屑尺寸约5~6cm,形状多呈片状、条状,很可能是井周地层沿层理剪切破坏而造成井眼失稳,计算结果与实际情况基本吻合,也验证了上文方法的合理性和可行性。因此,页岩中层理等弱面的剪切破坏可能是该地区页岩气水平井钻井中井壁垮塌的主要力学机制。另外,由于该井钻进过程中地层一直处于正压差作用,钻井液与页岩接触后的物理化学作用,加之该井采用了合成基钻井液,钻井液滤液沿层理侵入地层,导致井周地层孔隙压力增大,从而降低了层理等弱面上的有效应力和强度,使层理等弱面的抗剪强度降低,使实际坍塌压力当量密度远高于上文计算结果,最终导致井周页岩地层沿弱面剪切滑移而坍塌失稳。因此,建议后续研究中考虑井周压力传递和物理化学作用等因素的影响,形成更加完善的层理页岩水平井井眼稳定分析方法。
6 结 论
1)基于Mohr-Coulomb弱面强度理论,结合井周弹性应力分布模型和坐标转换关系,建立了层理页岩地层井周剪切失稳区域预测方法,可以分别计算出井周地层沿弱面剪切、本体剪切和全部剪切失稳区域的分布情况。
2)层理性页岩存在显著的强度各向异性特征,页岩弱面与本体强度参数基本呈线性关系,本体内聚力大约为弱面的2.10倍,而本体内摩擦角大约为弱面的1.20倍。
3)在层理等弱面影响下,水平井井周地层更加容易沿弱面剪切滑移破坏,增大页岩水平井井周地层失稳的风险,井周失稳区域扩大显著,而且失稳区域的形状并不是传统的“狗耳朵”形状,失稳后的井眼形状类似于长方形。
[1]Li Yufei,Fu Yongqiang,Tang Geng,etal.Effect of weak bedding planes on wellbore stability for shale gas wells[R].SPE 155666,2012.
[2]刘忠飞,何世明,全家正,等.川西首口页岩气水平井钻井技术[J].石油钻采工艺,2014,36(1):18-21.Liu Zhongfei,He Shiming,Quan Jiazheng,etal.Drilling technology for the first shale gas horizontal well in West Sichuan[J].Oil Drilling & Production Technology,2014,36(1):18-21.
[3]王红岩,刘玉章,董大忠,等.中国南方海相页岩气高效开发的科学问题[J].石油勘探与开发,2013,40(5):574-579.Wang Hongyan,Liu Yuzhang,Dong Dazhong,etal.Scientific issues on effective development of marine shale gas in Southern China[J].Petroleum Exploration and Development,2013,40(5):574-579.
[4]马天寿,陈平.基于CT扫描技术研究页岩水化细观损伤特性[J].石油勘探与开发,2014,41(2):227-233.Ma Tianshou,Chen Ping.Studies of meso-damage characteristics of shale hydration based on CT scanning technology[J].Petroleum Exploration and Development,2014,41(2):227-233.
[5]Aadn∅y Bernt Sigve.Stresses around boreholes drilled in sedimentary rocks[R].SPE 17119,1987.
[6]Dusseault M B,Gray K E.Mechanisms of stress-induced wellbore damage[R].SPE 23825,1992.
[7]Ong S H,Roegiers J C.Influence of anisotropies in borehole stability[J].International Journal of Rock Mechanics and Mining Sciences& Geomechanics Abstracts,1993,30(7):1069-1075.
[8]Okland D,Cook J M.Bedding-related borehole instability in high-angle wells[R].SPE 47285,1998.
[9]Al-Bazali T M,Zhang J,Wolfe C,etal.Wellbore instability of directional wells in laminated and naturally fractured shales[J].Journal of Porous Media,2009,12(2):119-130.
[10]Lee H,Ong S H,Azeemuddin M,etal.A wellbore stability model for formations with anisotropic rock strengths[J].Journal of Petroleum Science and Engineering,2012,96/97:109-119.
[11]金衍,陈勉.井壁稳定力学[M].北京:科学出版社,2012:13-66.Jin Yan,Chen Mian.Wellbore stability mechanics[M].Beijing:Science Press,2012:13-66.
[12]刘向君,叶仲斌,陈一健.岩石弱面结构对井壁稳定性的影响[J].天然气工业,2002,22(2):41-42.Liu Xiangjun,Ye Zhongbin,Chen Yijian.Influence of rock weak plane texture on sidewall stability[J].Natural Gas Industry,2002,22(2):41-42.
[13]袁俊亮,邓金根,蔚宝华,等.页岩气藏水平井井壁稳定性研究[J].天然气工业,2012,32(9):66-70.Yuan Junliang,Deng Jingen,Yu Baohua,etal.Wellbore stability of horizontal wells in shale gas reservoirs[J].Natural Gas Industry,2012,32(9):66-70.
[14]Lu Yunhu,Chen Mian,Jin Yan,etal.Influence of porous flow on wellbore stability for an inclined well with weak plane formation[J].Petroleum Science and Technology,2013,31(6):616-624.
[15]刘志远,陈勉,金衍,等.裂缝性储层裸眼井壁失稳影响因素分析[J].石油钻采工艺,2013,35(2):39-43.Liu Zhiyuan,Chen Mian,Jin Yan,etal.Analysis on wellbore stability of open hole in fractrued formation[J].Oil Drilling &Production Technology,2013,35(2):39-43.
[16]刘志远,陈勉,金衍,等.多弱面地层水平井裸眼井壁垮塌量分析[J].石油勘探与开发,2014,41(1):102-107.Liu Zhiyuan,Chen Mian,Jin Yan,etal.Calculation model for bore-hole collapse volume of a horizontal openhole in multiple-weak-plane formation[J].Petroleum Exploration and Development,2014,41(1):102-107.
[17]温航,陈勉,金衍,等.钻井液活度对硬脆性页岩破坏机理的实验研究[J].石油钻采工艺,2014,36(1):57-59.Wen Hang,Chen Mian,Jin Yan,etal.Experimental research on brittle shale failure caused by drilling fluid activity[J].Oil Drilling & Production Technology,2014,36(1):57-59.
[18]Chenevert M E,Gatlin C.Mechanical anisotropies of laminated sedimentary rocks[J].SPE Journal,1965,5(1):67-77.
[19]Lee H,Chang C,Ong S H,etal.Effect of anisotropic borehole wall failures when estimating in situ stresses:a case study in the Nankai accretionary wedge[J].Marine and Petroleum Geology,2013,48:411-422.
[20]蔡美峰,何满潮,刘东燕.岩石力学与工程[M].北京:科学出版社,2009:104-109.Cai Meifeng,He Manchao,Liu Dongyan.Rock mechanics and engineering[M].Beijing:Science Press,2009:104-109.
