北京地铁车站结构抗震分析
2014-11-27刘春阳张继清
张 鹏,刘春阳,张继清
(铁道第三勘察设计院集团有限公司,天津 300251)
随着我国国民经济的快速发展,城市化进程不断加快,城市轨道交通的建设对于缓解城市交通压力的作用日益明显。截至目前,我国城市轨道交通工程运营总里程约为1 800 km,运营车站约为1 200座,与地铁结缘的城市已达36个,一些二三线城市也积极准备上马城市轨道交通建设。我国是一个地震灾害频发的国家,许多城市都位于地震带上,而地铁工程又是城市的生命线工程,一旦破坏,生命财产和经济损失巨大。尤其是2008年汶川地震的发生,使得人们对地铁工程的抗震问题越来越重视。
目前对地铁地下车站结构的地震反应研究还处于初级阶段[1-3],主要的计算方法有地震系数法[4]、反应位移法、反应加速度法、时程分析法等。戚洪伟[5]、田雪娟[6]、陈磊等[7]、徐宏等[8]、宋林等[9]、鮑鹏等[10]曾分别采用了上述方法对车站的抗震性能进行了研究,但是对于抗震工况是否是现行地铁设计过程中的控制工况,结果却不尽相同。
以北京地铁14号线为背景,针对目前国内明、暗挖地铁车站中常见的4种结构断面形式,考虑结构使用过程中可能出现的荷载,按承载能力极限状态和正常使用极限状态分别进行荷载组合,其中又采用地震系数法和反应位移法两种抗震计算方法进行专项抗震计算研究,以期得出一些有益的结论。
1 工程概况
北京地铁14号线,全长47.4 km,全线共设车站37座,其中地下站35座。选取4座具有代表意义的车站结构断面形式进行抗震计算分析,它们分别是明挖两层三跨A站、明挖三层三跨B站、暗挖单层三跨C站以及暗挖两层三跨D站,车站横断面的具体尺寸详见图1。
各站分布的主要地层有(1)人工堆积层:粉土填土①层;杂填土①1层,该层土质不均,工程性质差。(2)新近沉积层:粉土②层:粉质黏土②1层;粉砂、细砂②3层;中砂~粗砂②4层;圆砾、卵石②5层。(3)第四纪沉积层:卵石、圆砾⑤层;粉质黏土⑥层;卵石⑦层;卵石⑨层。地下水位均在结构底板以下。抗浮设计水位在地表以下2~4 m考虑。
各站场地抗震设防烈度为Ⅷ度,设计基本地震加速度值为0.2g,设计地震分组为第一组。拟建场地类别为Ⅱ类。
2 结构静力计算
目前在地铁车站结构设计过程中,根据使用过程中结构上可能同时出现的荷载,主要有基本组合、抗震偶然组合、人防偶然组合,标准组合、变形验算、抗浮稳定验算等6种荷载组合,分别计算后取最不利值进行结构设计。
主要荷载有:结构自重(含装修荷载)、地下水压力、土压力、设备荷载(含管线荷载)、人群荷载、地面超载、地铁车辆荷载及其冲击力、混凝土收缩及徐变影响力、地层反力,地震荷载、人防荷载。主要荷载组合见表1。结构计算模型详见图2。
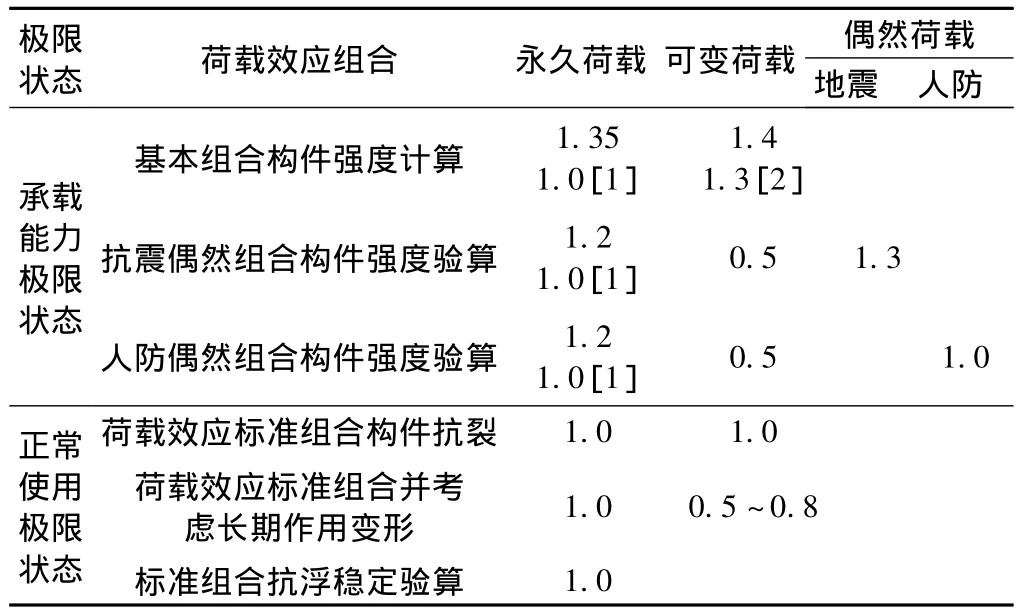
表1 荷载组合
3 地震系数法抗震计算
地震系数法作为一种静力法或拟静力法,对于一般地下结构,是现阶段我国地铁结构抗震设计中最为常用的方法,这种方法就是将随时间变化的地震力用等效的静地震荷载代替,然后再用静力计算模型分析地震荷载作用下的结构内力。等效的静地震荷载包括:结构本身的惯性力F1、结构上方土柱的惯性力F2、主动侧向土压力增量3部分[6]。计算简图见图3。
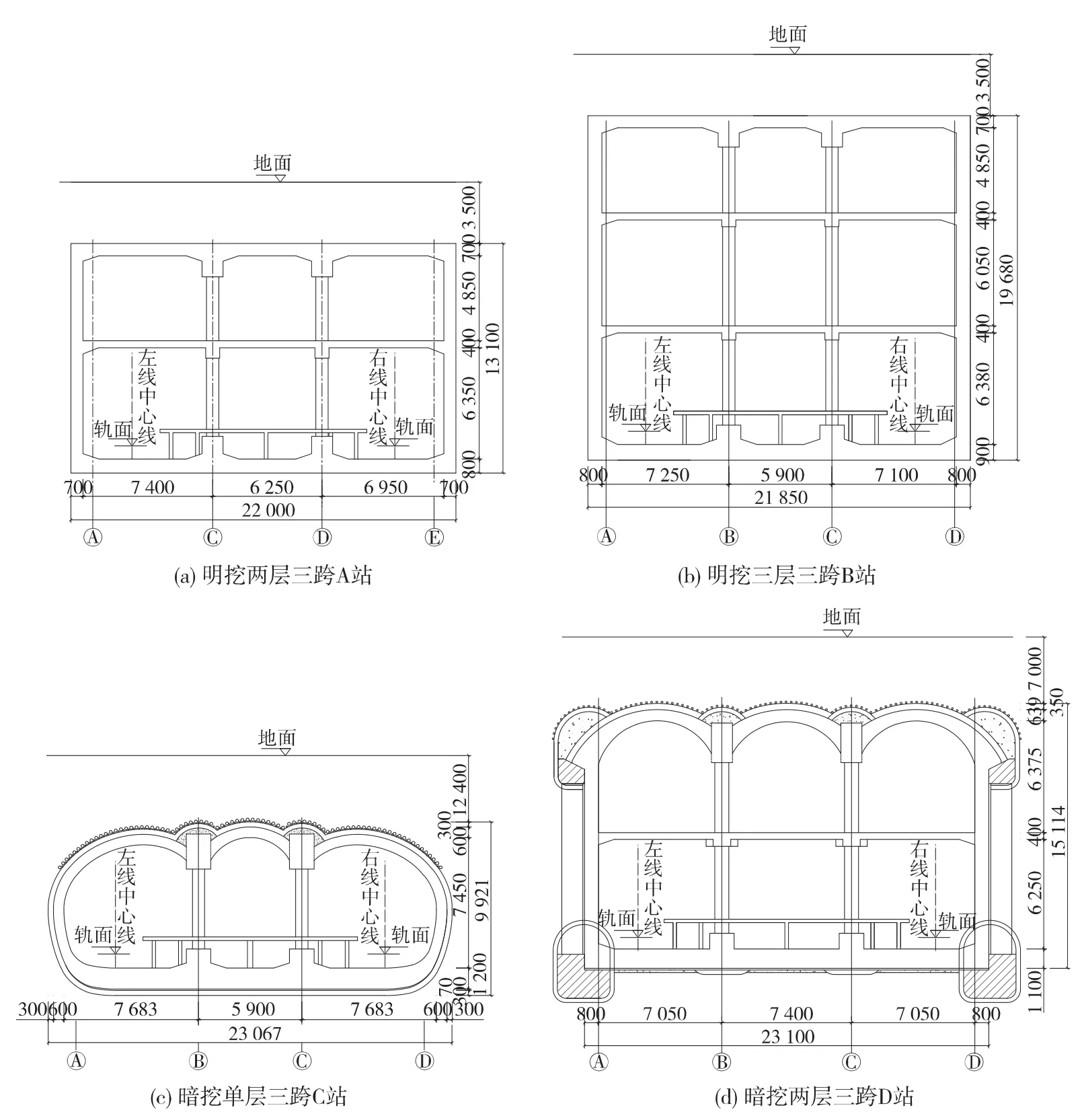
图1 地铁车站横断面(单位:mm)
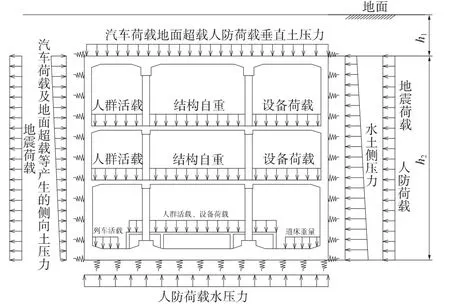
图2 主体结构使用阶段计算模型与荷载示意
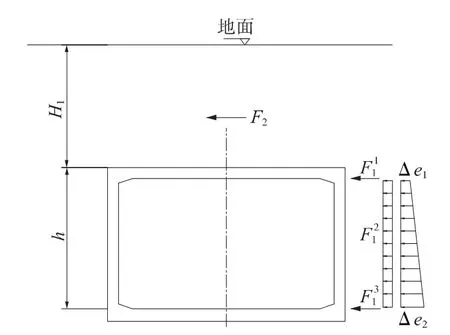
图3 浅埋框架抗震计算简图
3.1 结构的水平惯性力

式中 τ——作用于结构的地震加速度;
g——重力加速度;
Q——构件或结构的重力。
3.2 结构上方土柱的惯性力

式中 ηc——综合影响系数;
Kh——水平地震系数;
m上——上方土柱的质量。
3.3 主动侧向土压力的增量
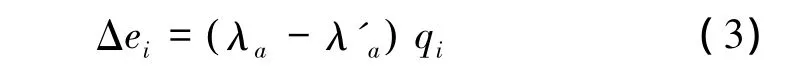
式中,λa=
4 反应位移法计算
反应位移法是用地震时周围土层的变形作为地震荷载,将土层动力反应位移的最大值作为强制位移施加于结构上,然后按静力原理计算内力。该方法符合地下结构地震时的振动特点,并且操作简单,因此在弹性范围内的计算,可优先考虑该方法。计算简图见图4。
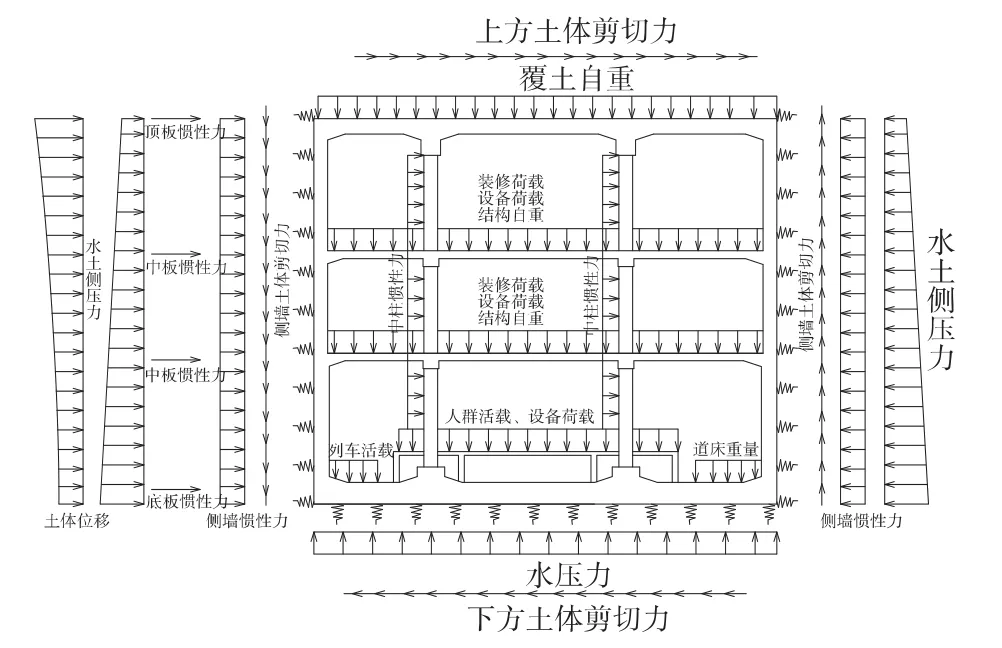
图4 横向地震反应计算的反应位移法
4.1 土层位移计算
进行地下结构地震反应计算时,应考虑土层相对位移、结构惯性力和结构周围剪力作用。土层相对位移、结构惯性力和结构周围剪力可由一维土层地震反应分析得到;对于进行了工程场地地震安全性评价工作的,应采用其得到的位移随深度的变化关系;对未进行工程场地地震安全性评价工作的,其土层位移沿深度和隧道轴向分布,地震时土层沿深度方向位移可按式(4)确定
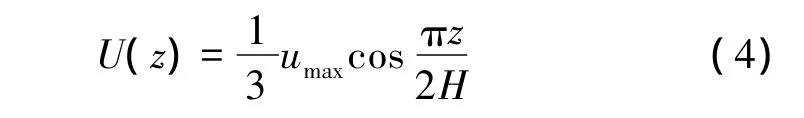
式中 U(z)——地震时深度z处土层的水平位移;
z——深度;
umax——场地地表最大位移;
H——地面至地震作用基准面的距离。
4.2 土体与结构相互作用弹簧刚度计算
计算模型中,结构周围土体采用地基弹簧表示,包括压缩弹簧和剪切弹簧;地基弹簧刚度按式(5)计算

式中 k——压缩、剪切地基弹簧刚度,kN/m;
K——地基反力系数,kN/m3;
L——地基的集中弹簧间距,m;
d——土层沿隧道与地下车站纵向的计算长度,m。
4.3 土层位移引起的作用于结构的地震力计算
在反应位移法中需将地下结构周围自由土层在地震作用下的最大位移(可取相对变形,相应于结构底面深度的位移为零)施加于结构两侧面压缩弹簧及上部剪切弹簧远离结构的端部。这里需要说明的是,由于在有限元软件中要实现在弹簧远离结构的一端施加强制位移较为困难,因此,可将强制位移按式(6)、式(7)转换为直接施加在结构侧壁和顶板上的等效荷载。
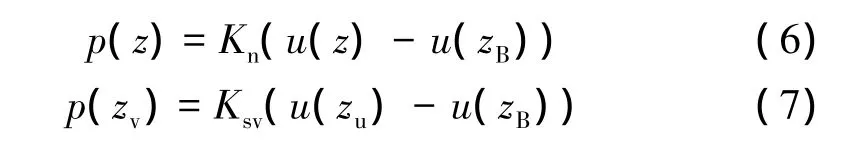
式中 p(z)——直接施加在结构侧壁上的等效荷载,kN;
p(zv)——直接施加在结构顶板的等效荷载,kN;
式中 u(z)、u(zB)、u(zU)——分别为距地表面深度z处、地下结构底板zB处和顶板zU处土层位移,m。
结构自身的惯性力可将结构物的质量乘以最大加速度来计算,作为集中力可以作用在结构形心上,也可以按照各部位的最大加速度计算结构的水平惯性力并施加在相应的结构部位上。结构上下表面的土层剪力采用反应谱法计算土层位移,通过土层位移微分确定土层应变,最终通过物理关系计算土层剪力。
5 计算结果及分析
分别对4种断面的5种荷载组合工况和2种抗震组合工况进行了计算研究,因断面和计算工况较多,仅列出明挖三层三跨B站和暗挖两层三跨D站反应位移法抗震计算的内力图。
5.1 明挖三层三跨B站抗震计算内力图(图5~图7)

图5 弯矩图(单位:kN·m)

图6 剪力图(单位:kN)
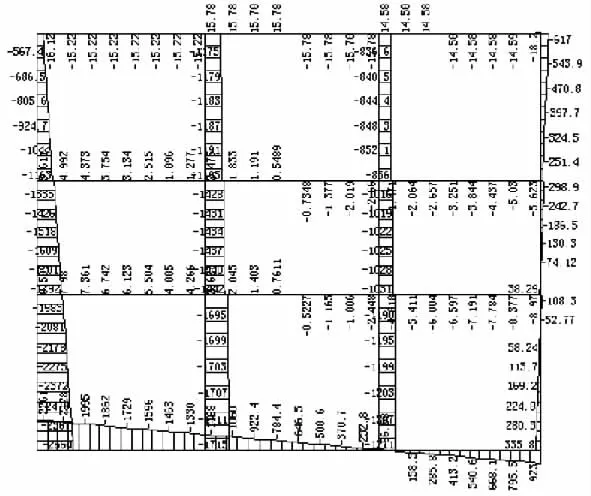
图7 轴力图(单位:kN)
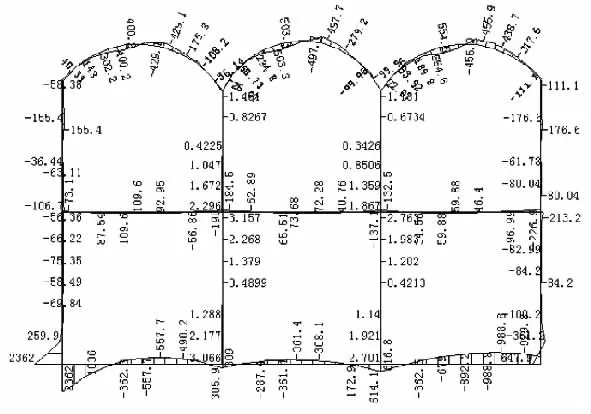
图8 弯矩图(单位:kN·m)
5.2 暗挖两层三跨D站抗震计算内力图(图8~图10)
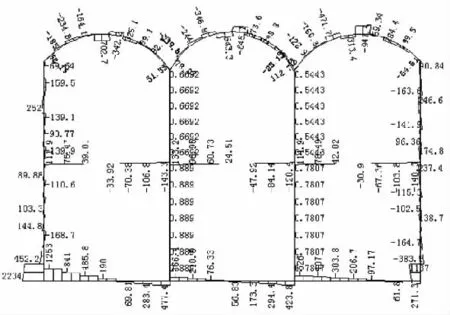
图9 剪力图(单位:kN)

图10 轴力图(单位:kN)
根据《地下铁道建筑结构抗震设计规范》(上海DG/TJ08-2064-2009)5.5条,结构构件截面的抗震验算时还需考虑承载力抗震调整系数γRE,抗震墙等构件调整系数按0.85考虑。
从图5~图10可以看出。
(1)在水平地震作用下矩形框架结构断面各构件的最大弯矩、剪力、轴力均出现在顶、中、底板与侧墙连接处;中板与中柱连接处的弯矩、剪力也较大;中柱的最大轴力发生在下柱与底板连接处。
(2)在水平地震作用下拱形框架结构断面的受力特点与矩形断面略有不同,顶板的最大弯矩、剪力、轴力都出现在边跨拱部,其余部分的受力与矩形断面相类似。
(3)经过计算分析,比较表1中基本荷载组合、标准荷载组合、地震荷载组合、人防荷载组合的计算结果,考虑到构件的承载力抗震调整系数,可以得出结论:在Ⅷ度地震作用下,车站结构各构件的控制组合多为标准荷载组合与人防荷载组合,地震荷载组合在地铁结构设计中不起控制作用。
6 结论
对北京地铁14号线4座断面形式各异的明、暗挖车站分别进行了设计过程中的荷载组合计算和抗震专项计算,得出以下结论。
(1)矩形框架结构断面车站的最不利受力位置为各层板与侧墙连接处,中柱与各层板的连接处。
(2)拱形框架结构断面车站的最不利受力位置为顶板边跨拱部、侧墙和中、底板连接处。
(3)加强以上薄弱部位的抗震设计,从截面尺寸(比如加掖)、构件配筋率、加密区长度、箍筋最大间距和最小直径和钢筋锚固长度等方面增强车站结构的整体抗震性能。
(4)采用地震系数法和反应位移法进行的抗震计算在地铁结构设计中不起控制作用。
[1]刘晶波,李彬.地铁地下结构抗震分析及设计中的几个关键问题[J].土木工程学报,2006,39(6):106-110.
[2]周健,苏燕,童鹏.软土地层地铁及地下构筑物抗震动力分析研究现状[J].地下空间,2003,23(2):173-178.
[3]GB50157—2003 地铁设计规范[S].
[4]施仲衡.地下铁道设计与施工[M].西安:陕西科学技术出版社,1997.
[5]戚洪伟.反应位移法在地铁抗震计算中的应用[J].铁道建筑技术,2012(S2):100-103.
[6]田雪娟.地铁车站抗震分析[J].铁道建筑技术,2012(6):67-73.
[7]陈磊,陈国兴,等.框架式地铁车站结构大地震近场地震反应特性的三维精细化非线性分析[J].岩土工程学报,2012,34(3):490-496.
[8]徐宏,卢登榜,等.南京地铁双层车站抗震分析[J].江苏建筑,2008(1):26-28.
[9]王良,惠丽萍.北京西客站地铁车站结构设计[J].铁道标准设计,1995(3):25-27.
[10]宋林,孟昭博,等.双层岛式地铁车站结构地震反应分析[J].世界地震工程,2010,26(2):187-192.
[11]鮑鹏,姜忻良,等.天津地铁土城车站地震反应分析[J].建筑结构,2001,37(1):99-101.
