盾构隧道近接浅埋式矩形隧道合理净距的研究

2014-11-27李岩松陈寿根周泽林

铁道标准设计 2014年1期

李岩松，陈寿根，周泽林

(西南交通大学交通隧道工程教育部重点实验室，成都 610031)

随着我国城市建设的不断发展，地下建筑也在不断发展，地铁建设过程中不可避免的出现了小净距重叠隧道的情况。隧道开挖使围岩受到扰动，继而波及附近围岩，当隧道之间距离很接近时，附近的围岩又会对已建成隧道造成影响，这使得土体力学行为变得极为复杂。因此，对小净距隧道的研究变得极为重要。国内外已经对该类工程进行了相关研究，也取得了很多成果。如王明年等人［1］以红岭中路－老街－晒布段区间重叠隧道为背景，对34种工况进行模拟分析后，对小净距重叠隧道重叠段近接分区进行研究，为重叠段区间隧道的设计与施工提供了理论支撑;李朋等人［2］对武汉地铁2号线1期工程和4号线1期工程中建设的4孔交叠盾构隧道进行了三维有限元模拟，分析盾构掘进对地表沉降的影响，以及后挖隧道对先挖隧道变形与受力的影响。虽然国内外已经对小净距隧道进行很多研究，但在对上部为浅埋式矩形闭合框架隧道，下部为双线盾构隧道的小净距重叠隧道工程的研究还是比较少的。因此，极有必要对在该种工程条件下引起的围岩力学行为进行研究。

1 工程概况

深圳地铁11号线起于福田站，终至碧头站，线路全长51.73 km(其中地下线长34.99 km)，最高运行速度为120 km/h。深圳地铁11号线具备快速联系城市中心区与西部片区的功能，同时兼顾机场快线功能，串联了福田中心区、南山、前海、机场、福永、沙井、松岗等片区。本项研究的工程背景为深圳地铁11号线南山—前海湾区间隧道。

深圳地铁11号线南山—前海湾区间隧道东起桂庙路路口，在桂庙路下向西穿行，经过前海路、月亮湾大道和平南铁路后，进入前海片区，最后到达前海湾站，全长约3.627 km。隧道穿越的地层主要为砾质黏性土、全强风化花岗岩、个别地段为淤泥、砂层、填石层、孤石和基岩凸起等。区间隧道(并行盾构隧道)埋深17.6～29.3 m，线间距13.0～19.2 m，采用盾构法施工，与先期建设的桂庙路下穿隧道(在区间隧道上方，宽37.1 m，高7.1 m，明挖法施工)重叠(上下重叠隧道)约2.2 km(双线)，区间隧道与桂庙路下穿隧道的最小净距仅为1.0 m。

2 计算模型及参数的确定

2.1 有关假定和计算前提

(1)设各土层为各向同性材料，无节理、裂隙，且水平分布。(2)在计算中将各向不连续盾构装配式衬砌视为连续均质圆筒，不考虑衬砌管片横向和纵向连接。(3)通过分别改变上下重叠隧道、水平并行隧道之间净距来模拟多种工况下(共60种工况)隧道围岩力学行为。如图1所示，计算时矩形闭合框架隧道埋深A始终为3 m，双线盾构隧道与矩形闭合框架隧道净距 B 分别取 1、2、3、4、5、6、7、8、10、12 m。双线盾构隧道净距 d 分别取 3.3、4.3、5.3、6.3、7.3、13.3 m(净距为 0.5D、0.65D、0.8D、0.95D、1.1D、2D(D 为隧道外径，D=6.7 m))。(4)为了在一定程度上反应地层注浆对盾构隧道的影响，本文设定注浆材料在计算时强度逐渐增强。并且，假定注浆层厚度为盾尾空隙，即与盾壳厚度相等，为10 cm。(5)对盾构通过时盾壳附近的围岩参数进行一定程度的折减，用来模拟盾构推进所产生的地层损失。(6)土层、衬砌及注浆层材料均设定服从Mohr-Coulomb屈服准则。(7)在进行地应力平衡计算时将土层的抗拉强度取较大值，以保证计算收敛。而在后续计算中将抗拉强度再改回实际值。(8)矩形闭合隧道开挖计算，然后进行隧道左线开挖计算，后进行隧道右线开挖计算［3-5］。

图1 隧道分布示意

2.2 有限元计算模型建立

鉴于工况较多且模型尺寸大，为简化并加速计算，本次计算采用FLAC有限差分软件，在纵向上取1 m厚度进行二维模拟计算［6-7］。模型尺寸宽150 m(矩形闭合框架单跨18 m，左右各取3倍跨长)，高80 m(模型底部距离隧道底部最小距离约为50 m，约为矩形闭合框架隧道高的5倍)。根据计算需要，计算模型如图2所示。

图2 隧道计算模型

2.3 计算参数

结合深圳地铁11号线南山—前海湾区间隧道地质报告，模型计算采用的地层及材料参数见表1。

表1 地层及材料参数

3 计算结果分析

在对模拟结果进行分析总结后，提出矩形隧道的管幕作用(图3)。上部矩形隧道由于宽度大，整体刚度大，对围岩有一定的支挡作用，其结构类似于管幕结构［8］。在摩尔-库伦模型中土体的剪切破坏面与最大主应力之间的夹角为(45°+φ/2)，根据摩尔－库伦模型土体剪切破坏角，估算出上部矩形隧道管幕作用影响范围大致为沿剪切破坏面(45°+φ/2)角度，以矩形隧道宽度为底边的闭合等腰三角形区域。在此区域内的地下结构均受管幕效应的影响，且距离矩形隧道越近，影响越大。

图3 管幕作用示意

3.1 地表及拱顶沉降分析

图4为地表沉降与上下隧道净距曲线图，地表沉降随上下隧道净距的增大而增大(在净距达到12～14 m时盾构隧道进入全风化片麻状花岗岩地层，这与黏性土层在性质上有较大差别，所以导致沉降值突然减小)，但整个曲线呈下凸状，说明地表沉降随埋深增大而增大，但增大的趋势越来越小，这种情况是多种因素作用的结果。首先，由于上部矩形隧道跨度大(单跨18 m，总宽度约37 m)且刚度大，当盾构隧道与浅埋式矩形隧道重叠修建时，上部矩形隧道管幕作用明显，对围岩有一定的支挡作用，从而对土层应力、地层变形、结构位移有一定的改善作用。其次由于盾构隧道埋深较浅土体应力小，所以地层沉降、拱顶沉降很小。

图4 地表沉降与上下隧道净距曲线

盾构隧道与矩形隧道距离较近时，管幕作用(图4)明显，但当盾构隧道与矩形隧道距离越来越大时，管幕作用下降。如图5所示，净距从1 m增加到2 m时拱顶沉降增加量最多，再加上上下隧道净距增大，埋深增大，隧道上部土压力增大，使得隧道拱顶沉降增大，地表沉降也随之增大。但随着盾构隧道埋深加深，地表沉降的增加量在减小，最终沉降趋于稳定。

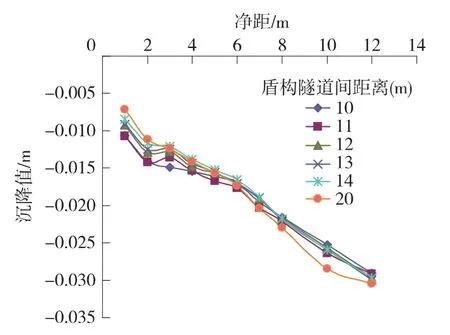
图5 拱顶沉降与上下隧道净距曲线

从图4和图5还可以看到，当埋深相同时地表沉降随盾构隧道净距增大而减小，证明随着平行隧道净距的增大，土层应力状态有明显的改善。再加上上部矩形隧道的管幕作用，在盾构隧道埋深较浅时地表沉降只有几毫米甚至是零沉降。

3.2 盾构隧道中央夹岩竖向应力分析

选取盾构隧道圆心连线中点处的夹岩竖向应力进行比较。如图6所示，在上下重叠隧道净距不变的情况下，中央夹岩竖向应力随着两隧道净距的增大而减小，当上下重叠隧道净距较大时(大于10 m)，图6与文献［9］中“中央夹岩核心区竖向应力与净距的关系曲线图”吻合的较好，即:当两隧道净距减小到一定范围时，中央夹岩竖向应力迅速增大。但当上下隧道重叠净距较小时(小于8 m)，中央夹岩应力变化不明显，甚至可以视为线形变化或无变化。出现这种现象与上部矩形隧道的管幕作用是分不开的。

图6 水平隧道间距与中央夹岩竖向应力曲线

3.3 塑性区分析

在有上部矩形隧道的情况下塑性区的分布也与往常的重叠隧道不同。在盾构隧道近接分区的分析中［1］横向近接影响范围为2.5D，竖向近接影响范围为3.5D，根据屈服接近度(yield approach index)的概念［10］，可以知道近接并行盾构隧道围岩力学效应优于近接重叠盾构隧道。但是在管幕作用的影响下，近接重叠隧道围岩力学效应优于并行盾构隧道。

在上下重叠隧道净距较小时(净距小于0.5D)，盾构隧道上部土层较薄，拱顶土层松动使塑性区呈拉伸破坏。盾构隧道之间夹岩塑性区随盾构隧道净距的增大而减小，在两隧道间净距为13.3 m时(2D)塑性区不再连通，围岩稳定性有很大改善。当上下重叠隧道净距逐渐增大时，拱顶受拉区面积逐渐减小，在净距为4 m(0.6D)时，拱顶受拉破坏塑性区消失。

在对塑性区的分析中发现:竖向塑性区在净距0.6D时就已经消失，而横向塑性区在净距1.8D时才不再连通，这说明在管幕作用的影响下近接重叠隧道围岩力学效应是优于并行盾构隧道的。

在上下重叠隧道净距4 m、并行盾构隧道净距13.3 m时出现了“W”状塑性区，塑性区沿盾构隧道左线、右线分别向左上和右上延伸，这与管幕效应影响边界大致相同。当上下重叠隧道净距6 m、并行盾构隧道净距13.3 m时，“W”状塑性区已经非常明显(图7)。

图7 工况B=6 m、C=20 m时的塑性区

当并行盾构隧道净距较小时，围岩受力复杂，中央夹岩处塑性区连通，围岩稳定性受到影响，随着盾构隧道净距的增加，围岩应力得到了很大改善，塑性区变小，且逐渐不连通。但当净距继续增大时，“W”状塑性区出现，塑性区面积反而急剧增大，这对隧道稳定性很不利。

在对所有工况的塑性区进行分析后，发现隧道塑性区的分布尤其是“W”状塑性区的出现位置与管幕效应影响区域密切相关。即:随着上下重叠隧道净距增大，“W”状塑性区出现时左右隧道净距越来越小。“W”状塑性区总是沿着管幕效应影响区域边界出现。虽然上下重叠隧道净距增大时隧道间相互影响变小，并行盾构隧道拱顶土体不会产生拉伸破坏，但是塑性区却呈由“W”或“X”状延伸。这说明:当上下重叠隧道净距过大或者并行盾构隧道之间净距过大时，土体会沿管幕效应影响边界(与水平面约呈(45°+φ/2)角度)发生剪切破坏。

分析后还发现，3条隧道中央夹岩的围岩稳定性必须受到重视。无论是在净距均最小时还是在净距均最大时，中央夹岩的塑性区面积都很大，并且只在上下隧道重叠净距小于5 m且并行盾构隧道净距很大(2D)时塑性区不连通，而在其他工况下塑性区始终连通，甚至在上下重叠隧道净距12 m、并行盾构隧道净距13.3 m时仍然连通，并且没有改善迹象。因此，在隧道修建时有必要对三条隧道的中央夹岩进行加固，以确保隧道的安全、稳定。