轨道与电枢间运动电磁场分布的数值计算
2014-11-27杨玉东付成芳赵环宇
杨玉东,付成芳,薛 文,赵环宇
(1.淮阴工学院 电子与电气工程学院,江苏 淮安 223003;2.南京理工大学 电子工程与光电技术学院,江苏 南京 210094)
在固体电枢电磁发射器发射结果检测中发现轨道的内侧及电枢后尾部经常会出现烧蚀现象,经研究表明,这种现象是由于电枢高速运动时,轨道和电枢中电流密度分布不均匀造成的,电流密度聚集在轨道和电枢的尾部,使得局部区域的电流密度过大,该局部温度急剧上升,造成轨道材料的烧蚀[1-4]。描述轨道和电枢相对运动的电磁方程在数学上属于对流扩散方程,目前有多种方法求解对流扩散方程,如有限差分法、有限元法和边界元法等,但每种算法均容易出现数值扩散或解的振荡解等问题,尤其是对流项占优情况下。如文献[5]采用有限差分法对对流项占优的对流扩散方程求解,离散过程中对离散时间步长采用细化,用于提高速度项,实质上是采用弱化对流项方式进行求解,一旦时间过长或速度项过高,如速度超过800m/s时就会出现扩散及振荡现象,因此如何恰当处理对流项成为解对流扩散方程的关键。有限元或迎风差分格式虽然能在一定程度上消除解的振荡,但数值扩散现象很严重,即使采取更高的精度格式也难于解决此类问题[6]。目前一种求解对流扩散反应型方程的算子分裂格式DF-AD-REA (扩散-对流-反应)被广泛应用于对流扩散方程的求解。在规则网格上,处理对流扩散算子和反应项时,可以分别采用不同的各自最适应其算子的数学物理特征的格式[7]。笔者采用算子分裂格式处理轨道和电枢间运动电磁场方程,计算出在激励电流作用下运动导体内部电磁场参数的分布,揭示电磁发射过程中出现的速度趋肤效应现象,为选择合适的轨道、电枢材料和形状奠定一定的理论基础。
1 控制方程
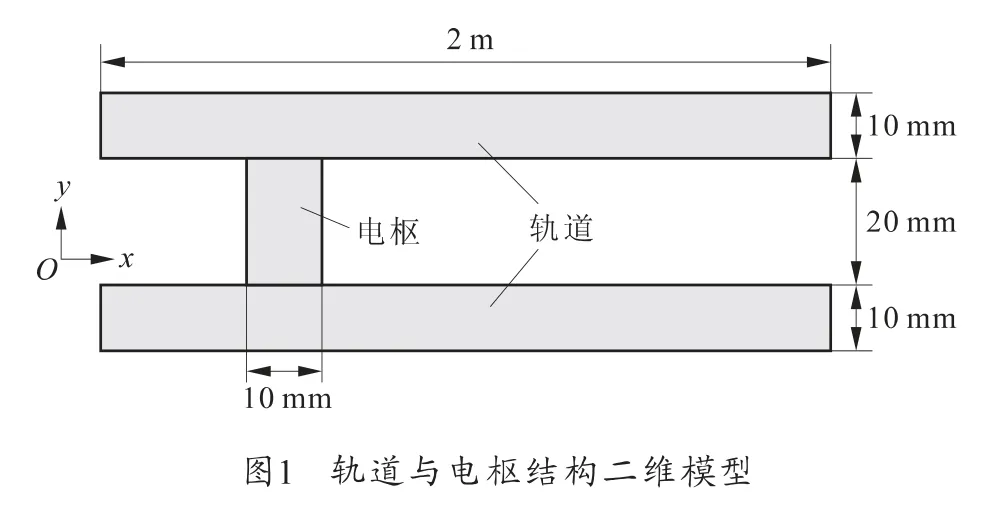
固体电枢与轨道之间联系是电接触式,电枢固定,电枢与轨道间滑动接触,激励源从轨道的两端加入,其结构及其二维模型如图1所示。
由Maxwell方程组可推导出轨道和滑动电枢内部电磁场分布方程:
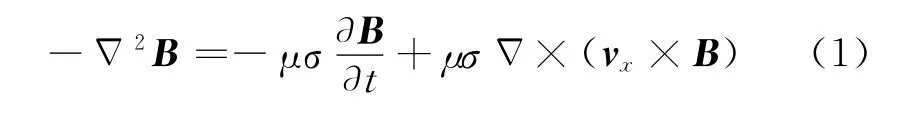
式中:B为导体中磁感应强度;μ为导体的磁导率;σ为导体的电导率;t为磁场扩散时间;vx为沿着x轴方向的速度。在二维坐标中,式(1)可写成如下偏微分方程形式:
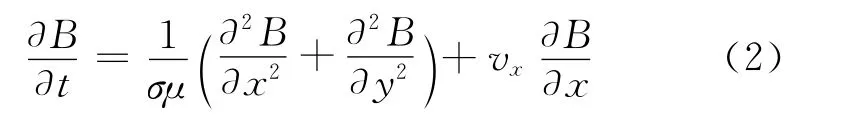
2 计算方法
目前算子分裂法用于求解对流扩散方程已成为有效的方法之一,其优点是算子分裂后的方程简单、容易求解且格式灵活,稳定性好。算子分裂方法主要有:标准的Lie分裂、Strang分裂和Sourec分裂[8],笔者将采用Strang分裂算法,把对流项和扩散项分别分解为两个算子。
2.1 算子分裂格式
对于式(2)采用Strang算子分裂.在每一个时间步[tn,tn+1]采用如下A、B分裂格式:
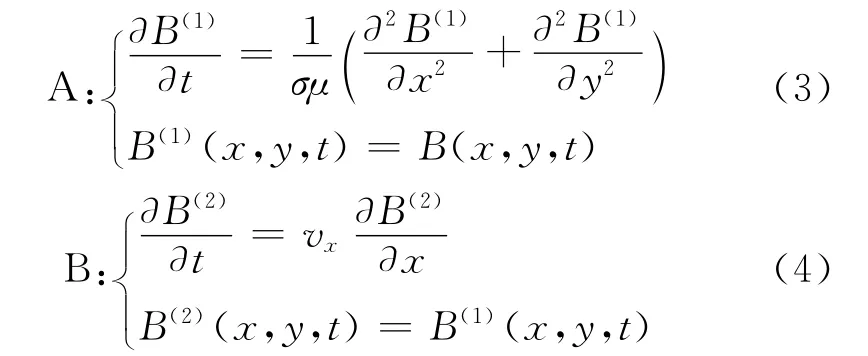
式中,A 格式为扩散项表达式,B格式为对流项表达式。式(3)中第二个表达式是A 格式的边界值和初始值,其含义是A 格式中的初始值和边界值,采用式(2)的初始值和边界值;式(4)中第二个表达式是B格式的边界值和初始值,其采用的值为A 格式计算后得到的值。A、B 两格式顺序计算,B 格式计算的结果就是一个时间步结束后,最终得到的结果。即B(x,y,tn+1)≈B(2)(x,y,tn+1)。
2.2 激励源设置
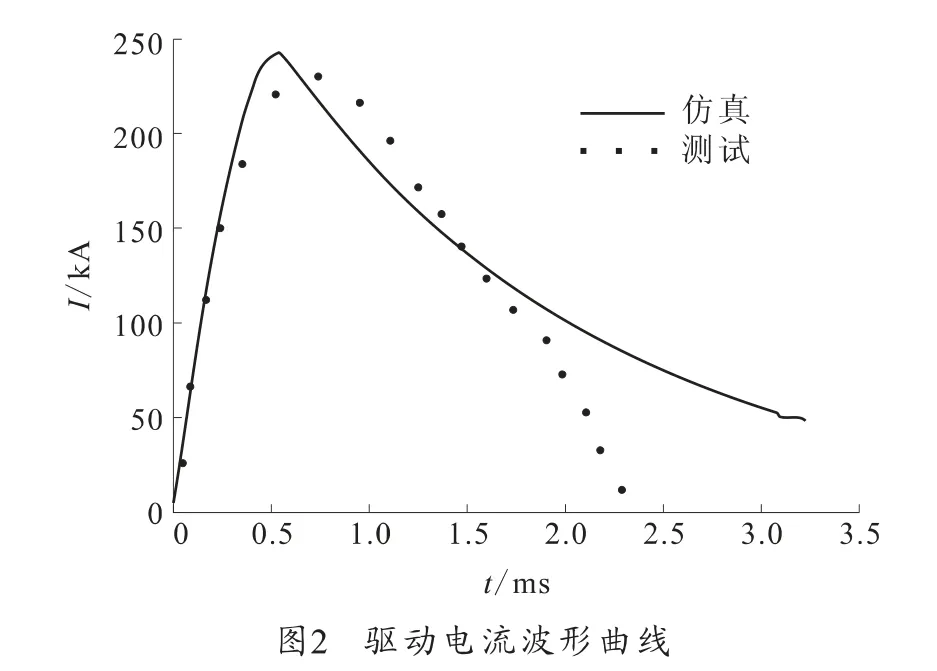
激励源采用8 个单模块脉冲成形网络同时触发,电路参数为:轨道长度2m,电枢质量为45g,平均电感梯度为0.46μH/m,每个模块中储能电容容量为15mF,调波电感为60μH,电容充电电压为4 kV,总能量为12kJ,驱动电流波形如图2所示。
激励电流密度可用如下函数近似描述:
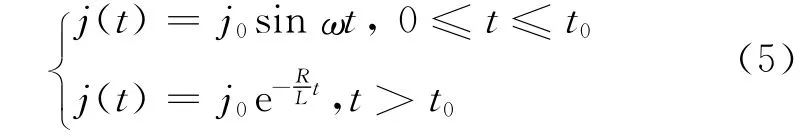
式中:ω=,S为轨道x轴方向横截面面积。
经仿真计算可得到电枢运行速度与时间的关系如图3所示。
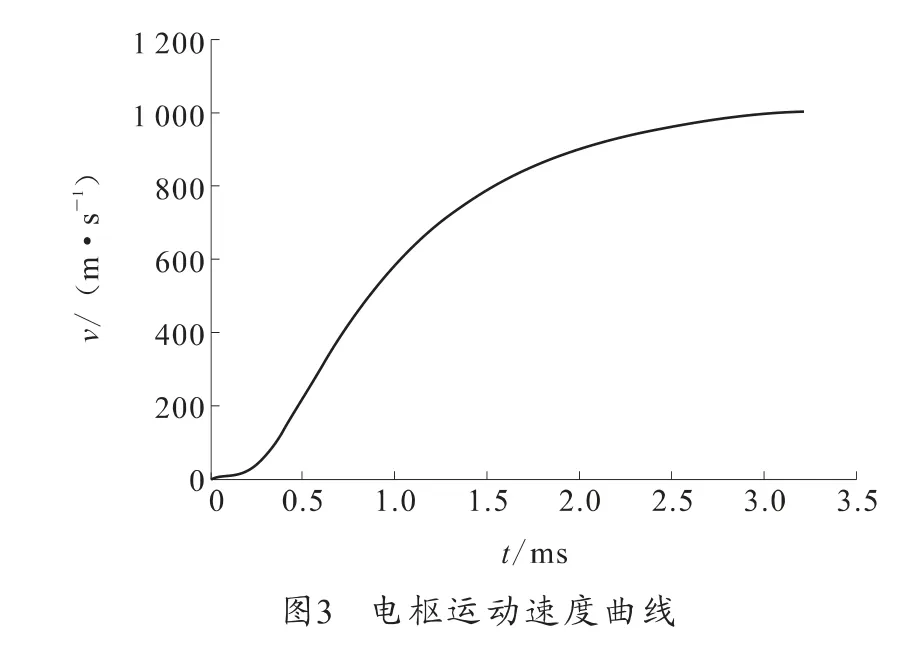
2.3 初始条件和边界条件
设轨道和电枢内部的初始磁感应强度和电流密度为0;以0时刻为计算时间,此时在轨道两端施加激励电流,当时间步长k=1时,电枢的左边界磁感应强度为两轨道产生的磁感应强度的叠加,B=2μj;轨道的左下边界、电枢左下侧边界为B=μj;右侧下边界B=0,在后续的计算过程中,电枢左侧边界条件一直保持为B=2μj,右侧边界为B=0;上下边界条件为∂B/∂y=0;轨道边界条件左侧∂B/∂x=0;右侧和上边界B=0[9-10]。
2.4 中间条件
考虑到A、B计算格式的顺序性,先计算电磁场的扩散运动,再计算电磁场的对流运动。A 格式反映的是轨道和电枢中外部激励电流在导体内部引起的磁感应强度随着时间由外至内逐步扩散的过程;B格式反映的是电枢运动过程中切割磁力线引起的感应电流在导体内部产生的磁感应强度的变化,其中间量是有物理意义的。电枢运动产生的在导体内部的感生电流属于涡流,涡流的方向与外加电流方向相反,实际测量的轨道激励电流中已经包含了感生电流,因此,B格式中采用的边界条件应与A 格式中边界条件相同,B 格式计算的初始条件采用A 格式计算结果。
2.5 格式计算方法
为了与文献[5]相比较,笔者采取与文献[5]一致的格式剖分,即考虑到轨道和电枢外形是对称的,可选取轨道上半部分和电枢的上半部分作为计算区域,一半导轨被剖分为5 000×25个网格,一半电枢被剖分为25×25个网格[5]。为编程方便,设电枢相对于轨道静止,轨道相对于电枢作反向运动。因此用式(3)、(4)分裂格式计算时,轨道计算取速度为-vx;电枢计算取速度vx=0。即计算轨道磁感应强度分布采用A、B格式,而计算电枢中磁感应强度仅使用A 格式即可。
式(3)方程为二维抛物型方程,选择P-R格式进行离散。P-R 差分格式结构较为简单,无条件稳定,且具有二阶精度[11]。设离散格式x、y方向的空间步长为h,时间步长为τ,进一步推导可得式(3)的具体差分格式为
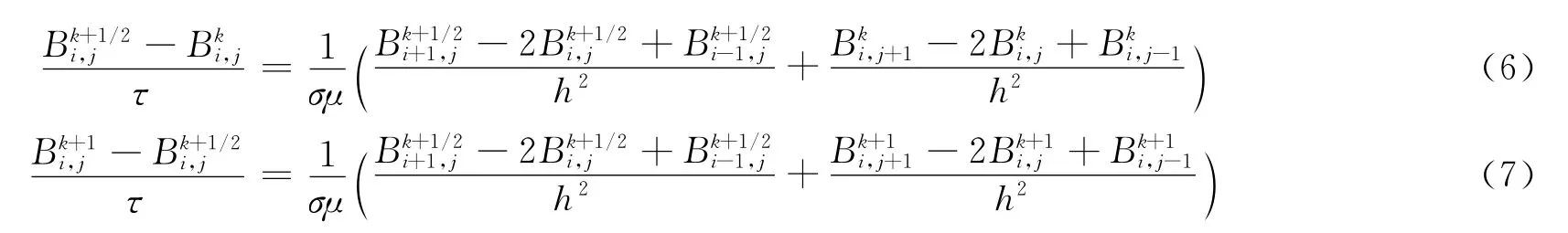
式(4)是一维一阶双曲型方程,选择如下Euler差分格式进行离散:
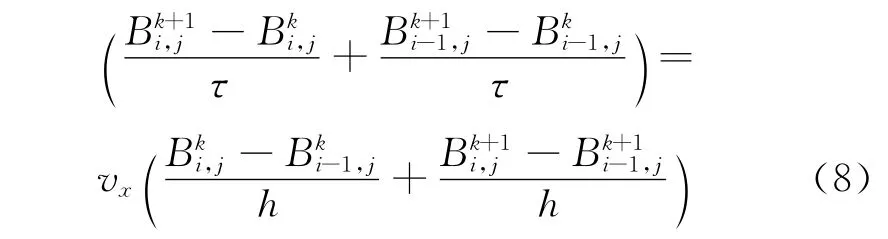
此差分格式具有二阶精度[11]。
当求得某时刻电枢和轨道内磁感应强度B后,根据▽×B=μJ,可相应地求出电流密度J在x、y轴方向的分量。
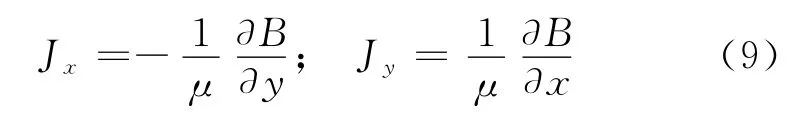
则J=
3 计算结果及分析
式(3)~式(4)的初始条件确定后,采用Turbo C 2.0编程计算得到0-3.5ms内不同时刻的轨道及电枢内部磁感强度和电流密度分布数据,部分数据经过Surfer处理后显示结果如图4和图5所示。1.02ms时刻,导轨、电枢内磁感强度最大值为0.7 T。此时电枢的运动速度为600m/s。最大磁感强度分布在轨道的下边缘和电枢左边缘,并由轨道下边缘向上、电枢左边缘向右递减扩散,在电枢的尾部集中;在2.78ms时刻,导轨、电枢内磁感强度最大值为1.2T。此时电枢的运动速度为972 m/s。随着电枢运行速度增加,磁感应强度在轨道内部向外面扩散的深度减小,而在电枢内部,向右深度扩散增强,并有扩散至电枢整个区域的趋势。
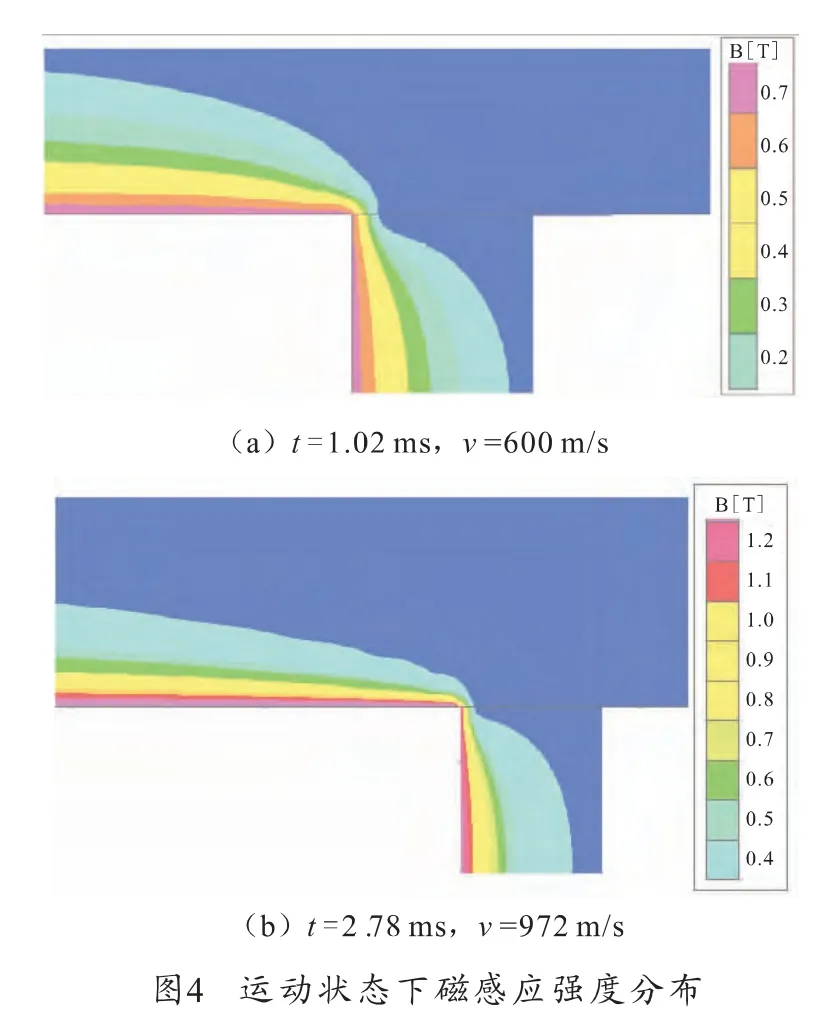
此计算结果、电磁场分布云图与参考文献[5]呈一致性,区别在于文献[5]在计算过程中,当速度项超过600m/s时,计算结果容易发散或出现振荡现象,即使对时间步长进一步减小到10-6,也只能使得速度限制在800m/s左右,计算过程耗时长且结果不稳定。而采用算子分裂格式时,当计算时长达到1.5ms以上,即时速度达到700m/s,时间步长仅为10-5时,计算数据依然稳定收敛。在不减小时间步长情况下,当计算至2.78 ms、即时速度为972m/s时,仍能得到稳定的计算结果。事实上式(3)为抛物型方程,其中不含速度项,采用P-R 格式是采用交替隐形格式进行求解,无条件稳定,具有二阶精度;不稳定的因素存在于式(4)中,式(4)为一维一阶双曲型方程,其稳定和收敛的条件为

式中λ=τ/h。则根据式(10)的条件,设时间步长为10-5,空间步长为10-2,则最大收敛速度可达到1km/s。欲提高速度项,可通过减小时间步长或增大空间步长来获得,如空间步长不变,时间步长减小至10-6,则速度可提高至10km/s。这是理论上分析的结果,实际上电枢运动的速度并不是线性增加的,当电枢运行至激励电流下降期,其加速度增加缓慢,速度变化需要更多的时间,反映在程序运行上,迭代的次数将成倍增加,严重耗费机时和内存。
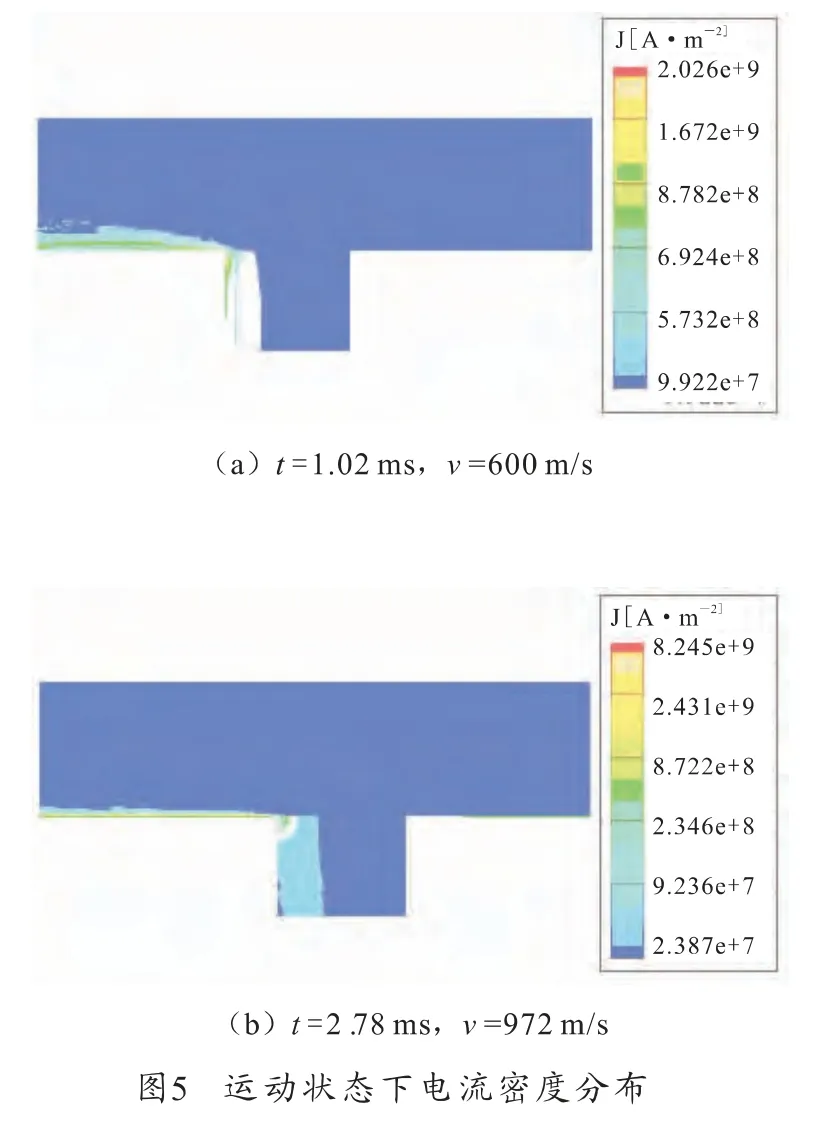
图5为瞬时电流密度在轨道和电枢内部的分布云图。1.02ms时刻轨道和电枢内的电流密度最大值约为8.8×108A/m2;2.78 ms时约为2.3×108A/m2,与图4对比可知,轨道和电枢内电流密度与磁感应强度分布规律是一致的,电流密度由边缘至导体内部扩散呈递减趋势,在轨道和电枢拐角处最大;随着速度逐渐增加,电流密度越来越趋近于轨道和电枢的内侧。这是因为:在静止情况时,导体中电流密度在短时间内会迅速扩散;而当电枢处于高速运动状态时,在轨道和电枢接触面的电流密度会被强行牵引至其尾部,使得电枢和轨道的边缘处,尤其电枢与轨道相接触局部区域电流密度最大[12]。尤其需要注意的是,当轨道的内表面及电枢的尾部的电流密度过于集中时,会引起接触区局部区域导体产生过高的欧姆热,从而引起局部区域温度短时间内迅速升高,当温度达到电枢及轨道材料的熔点时,会引起该区域的导体烧蚀,上述计算结果与文 献[5]、[9]、[10]、[12]结论和数据基本吻合。
4 结论
在高速运动的固体电磁发射过程中出现的速度趋肤效应是运动导体在强磁场中呈现的一种现象,是电磁场和热传递共同作用的结果,尤其在大电流、高速度情况下显得尤其突出。其结果会造成电枢和导轨局部区域出现烧蚀,使得难以进行多次发射,会大大降低电磁发射效率。建立了轨道和电枢内部电磁场分布的二维对流扩散方程,并采用算子分裂格式将方程分解为扩散方程和对流方程。因为扩散方程是抛物型方程,对其求解有稳定、精度较高的成熟算法,对流方程为一阶双曲方程,对其求解也比较简单。求解过程避免了对流项的存在造成方程数值振荡和扩散问题。数值计算过程表明,当速度达到972 m/s时,此时对流项绝对占优,计算数据仍然稳定收敛,避免了文献[5]中当电枢运动速度高时导致数据发散的现象。计算过程存在以下不足:模型中假设电枢与轨道间接触良好,不存在接触电阻,而在实际试验中发现两者的接触电阻是存在的,且是造成热损耗的一个重要因素;实际的电磁发射过程中,需要考虑运动、电磁场、热场之间的耦合关系,而这种耦合关系是极为复杂的,笔者对这种耦合关系处理较为简单,不可避免带来误差。还有其他若干不足地方不能一一列举,这将在今后的研究工作中加以逐步改进。
(References)
[1]MARSHALL R A.The distributed store railgun,its efficiency,and its energy store implications[J].IEEE Transaction on Magnetics,1997,23(1):582-583.
[2]KAMRAN D,RAHIMZADEH M.Dynamic response and critical velocity studies in an electromagnetic railgun[J].IEEE Transaction on Magnetics,2007,43(1):126-127.
[3]THOMAS G,ENGEL Jese M.Efficiency and scaling of constant inductance gradient DC electromagnetic launchers[J].IEEE Transaction on Magnetics,2006,42(8):2044-2047.
[4]DAVID A H.Analysis of startup behavior in a Cshaped armature using linked EMAP3D LDYNA3D finite element codes[J].IEEE Transaction on Magnetics,1999,35(1):60-62.
[5]杨玉东,王建新,薛文.轨道炮速度趋肤效应的分析与仿真[J].强激光与粒子束,2011,23(7):1965-1968.YANG Yudong,WANG Jianxin,XUE Wen.Simulation and analysis for velocity skin effect of railgun[J].High Power Laser and Particle Beams.2011,23(7):1965-1968.(in Chinese)
[6]POWELL J D,ZIELINSKI A E.Ohmic heating in a double-taper sabot-armature[J].IEEE Transaction on Magnetics,2003,39(1):153-157.
[7]贾宏恩,李开泰,钟贺.算子分裂法求解对流-扩散-反应方程[J].工程数学学报,2012,29(1):89-91.JIA Hongen,LI Kaitai,ZHONG He.An operator splitting scheme for advection-diffusion-reaction equation[J].Chinese Journal of Engineering Mathematics,2012,29(1):89-91.(in Chinese)
[8]曹志先,魏良琰.对流扩散反应型方程的一种稳定的算子分裂格式[J].水动力学研究与进展A 辑,1991,6(1):60-62.CAO Zhixian,WEI Liangyan.An operator splitting scheme with stability for advection-diffusion-reaction equations[J].Journal of Hydrodynamics,1991,6(1):60-62.(in Chinese)
[9]李昕,翁春生.固体电枢电磁导轨炮非稳态电磁效应[J].南京理工大学学报,2009,2(1):108-109.LI Xin,WENG Chunshen.Unsteady electromagnetic effection solid armature railguns[J].Journal of Nanjing University of Science and Technology,2009,2(1):108-109.(in Chinese)
[10]李昕,翁春生.U 型电枢非稳态电磁场二维数值模拟[J].火炮发射与控制学报,2009,(1):1-3.LI Xin,WENG Chunshen.Two dimension numericalsimulation of unsteady electromagnetic in U shaped solid armature[J].Journal of Gun Launch&Control,2009,(1):1-3.(in Chinese)
[11]孙志忠.偏微分方程数值解法[M].北京:科学出版社,2005:120-137.SUN Zhizhong.Numer methods partial differential eq[M].Beijing:Science Press,2005:120-137.(in Chinese)
[12]POWELL J D,ZIELINSKI A E.Observation and simulation of solid-armature railgun performance[J].IEEE Transaction on Magnetics,1999,35(1):84-89.
