椭圆齿轮齿根过渡曲线拟合*
2014-11-26刘永平县喜龙
□ 刘永平 □ 王 鹏 □ 县喜龙
兰州理工大学 机电工程学院 兰州 730050
一对相互啮合的椭圆齿轮,因其机构紧凑、传动平衡、能实现单向循环变速运动和一定要求的变速传动[1~4],在许多机械动力机构中都有应用并且在工业上的应用越来越广,故对椭圆齿轮的设计与加工有了更高的要求[5,6]。目前,生成非圆齿轮齿廓的方案一般有两种,一种是模拟实际加工的过程,用展成运动通过VC等来获得包络后的齿廓数据,并提取其齿廓数据至AutoCAD(CAXA)等软件中对数据进行处理,然后在UG(Pro/E)等软件中生成三维模型,并对其进行运动仿真,或在ANSYS(ADMAS)中进行动力学分析。另外一种方法是用折算齿形法来绘制非圆齿轮的渐开线齿廓。本文对生成椭圆齿轮齿廓的第二种方法进行了研究。
1 椭圆齿轮设计的理论基础
1.1 椭圆齿轮的节曲线设计
椭圆齿轮的节曲线是比较常见的封闭型节曲线,如图1所示,当椭圆齿轮的回转中心在左焦点上O时,椭圆的极坐标方程为:


▲图1 椭圆齿轮节曲线
圆齿轮的轮齿在分度圆上位置是可以任意分布的,但非圆齿轮的轮齿不能随意分布,由于其两个相互啮合的非圆齿轮的节曲线的切点位置是一一对应的[7],因此必须保证轮齿在非圆齿轮节曲线上均匀分布,即椭圆齿轮的轮齿须均匀地分布于其节曲线上。不失一般性,假设椭圆齿轮的齿数为z,模数为m,椭圆的节曲线的周长为L,即此三者必须满足:

1.2 椭圆齿轮齿廓的数学模型
非圆齿轮的齿廓形状可由齿形渐屈线的渐伸线来确定,而渐伸线可以由作图法获得,其理论基础为根据渐屈线的求长法来确定渐伸线。但非圆齿轮节曲线的曲率中心和齿形渐屈线的曲率中心没有公共轨迹,因此齿形渐屈线不可能是齿轮节曲线的法向等距线,所以求齿形的渐屈线并用数学方程量化的描述有困难[8]。故采取相对于上述齿形渐屈线的渐伸线较为简单的折算齿形法来绘制椭圆齿轮的齿廓。

▲图2 折算齿形法绘制椭圆齿轮齿廓
椭圆齿轮的齿形较渐开线圆齿轮要复杂得多,因为其任意一轮齿其左右齿形是不相同的。用折算齿形法生成椭圆齿轮的渐开线齿形的数学模型如图2所示。图中:O为椭圆齿轮节曲线中心也是坐标系YOX的坐标原点;ρ为折算齿形轮齿节曲线的曲率半径;O1既是ρ的端点,又是坐标系Y1O1X1的坐标原点;A为折算齿形渐开线4上任意一点;B为渐开线齿形4在A点的法线与基圆6的交点;C为渐开线齿形的起点;μ为O1C与O1B的夹角;β为X轴与O1B的夹角;m、n分别为坐标系Y1O1X1的原点在坐标系YOX中的横、纵坐标;1为椭圆齿轮的节曲线,2为齿顶曲线,3为折算齿形的左侧渐开线,4为折算齿形的右侧渐开线,5为曲率圆,6为基圆,7为齿根曲线。
对于渐开线右齿形4的方程在坐标系Y1O1X1中可描述为:

坐标系Y1O1X1中的坐标可以通过变换矩阵M01转换至坐标系YOX中,即:

2 齿根过渡曲线的设计
齿根的过渡曲线对齿轮的啮合性能没有影响,当用滚刀或齿条刀加工渐开线齿轮时,齿根过渡曲线会自然生成[9],但其对齿轮的齿根强度和寿命影响很大。如图2所示,从渐开线的起点C至椭圆齿轮的齿根曲线是没有渐开线的,即每一个折算后的轮齿,其基圆内无渐开线,故用折算齿形法绘制齿廓齿根过渡曲线,有时候是无法生成的,只能通过拾取已得到的渐开线上的数据来拟合,理论上只要拾取的数据足够多,采取的方法合理,那么拟合的曲线就会有足够的精度。
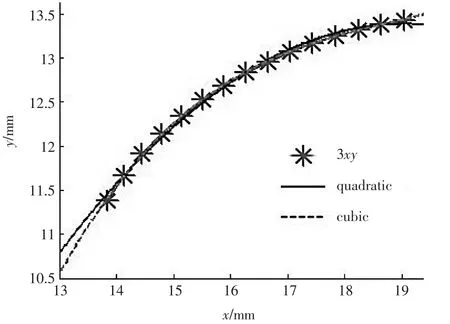
在图2中提取折算齿形渐开线3、4上的点见表1,用其坐标点拟合的曲线如图3、4所示。
图3中3xy为15个提取的样本点,quadratic为二次拟合曲线:

cubic为三次拟合曲线:

图4中4xy为15个提取的样本点,quadratic为二次拟合曲线:c
▲图3 渐开线3上点的拟合曲线

▲图4 渐开线4上点的拟合曲线

▲图5 椭圆齿轮折算齿形渐开线
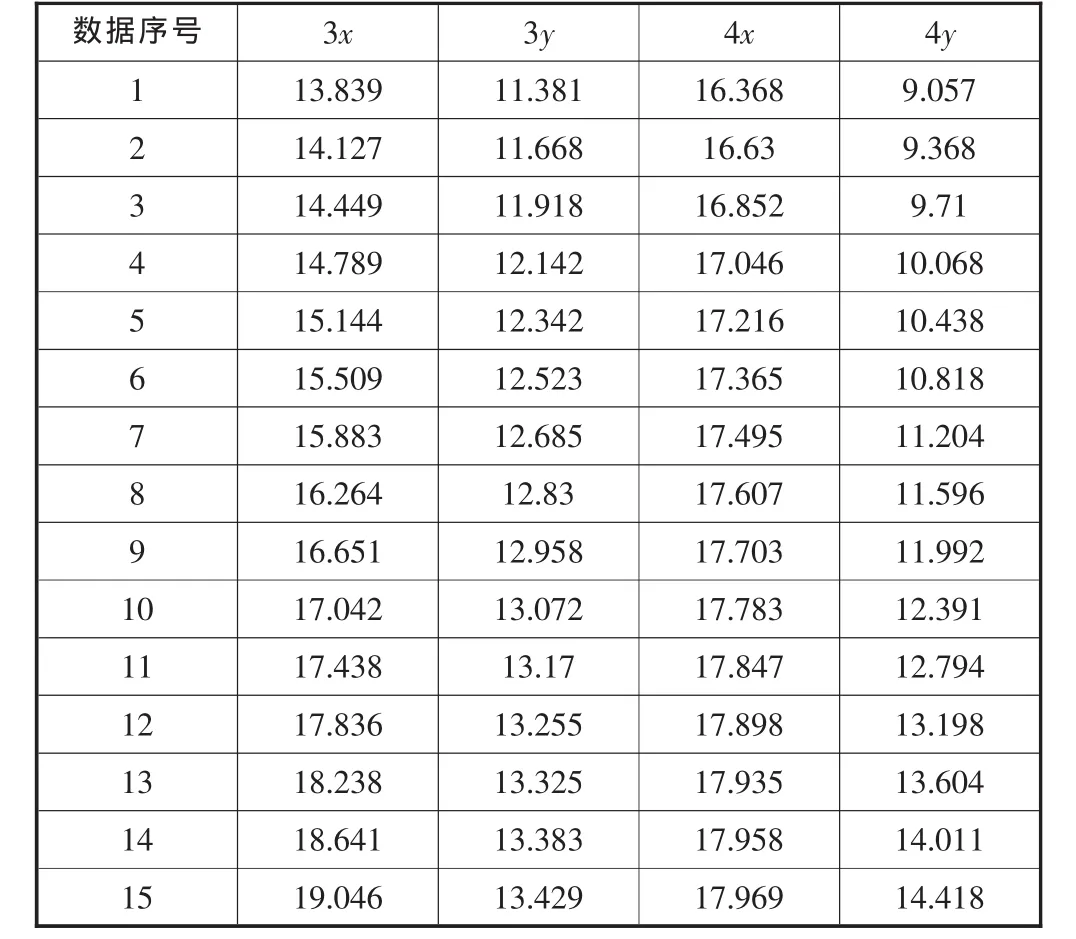
表1 渐开线3、4的坐标点/mm

ubic为三次拟合曲线:

通过上述图形可知,其拟合曲线采用三次拟合曲线方程较为合理。
用折算齿形法绘制齿廓时,从图5中可看到,在椭圆齿轮节曲线上不同点处,随着曲率半径的变化,渐开线至齿根曲线的距离是变化的,其趋势为随着曲率半径的增加,折算齿形渐开线的起点至齿根曲线的距离在减小,这在用折算齿形法绘制三阶椭圆时尤为明显,如图6所示。
因为圆齿轮分度圆大于基圆而齿顶圆大于齿根圆,但基圆和齿根圆的大小关系则不一定[10]。基圆直径和齿根圆直径分别为:


▲图6 三阶椭圆齿轮折算齿形渐开线
式中:ha*为齿顶高系数,一般为1;c*为顶隙系数,一般为0.25;α为刀具齿形角,一般为200。
当满足:Df≥Db,即:

将参数代入式(12)得:z≥41.454,即 z≥42 时,用折算齿形法可以得到整个齿廓曲线。
3 实例计算与说明
以椭圆齿轮为例。
实例1:当各参数为椭圆长半轴a=21.046 1 mm、短半轴b=16.836 9 mm、偏心率 e=0.6、模数 m=2 mm、齿数z=19时,如图5由对称性只须拟合X轴上方轮齿的数据即可,用上述方法拟合的三次曲线方程为:
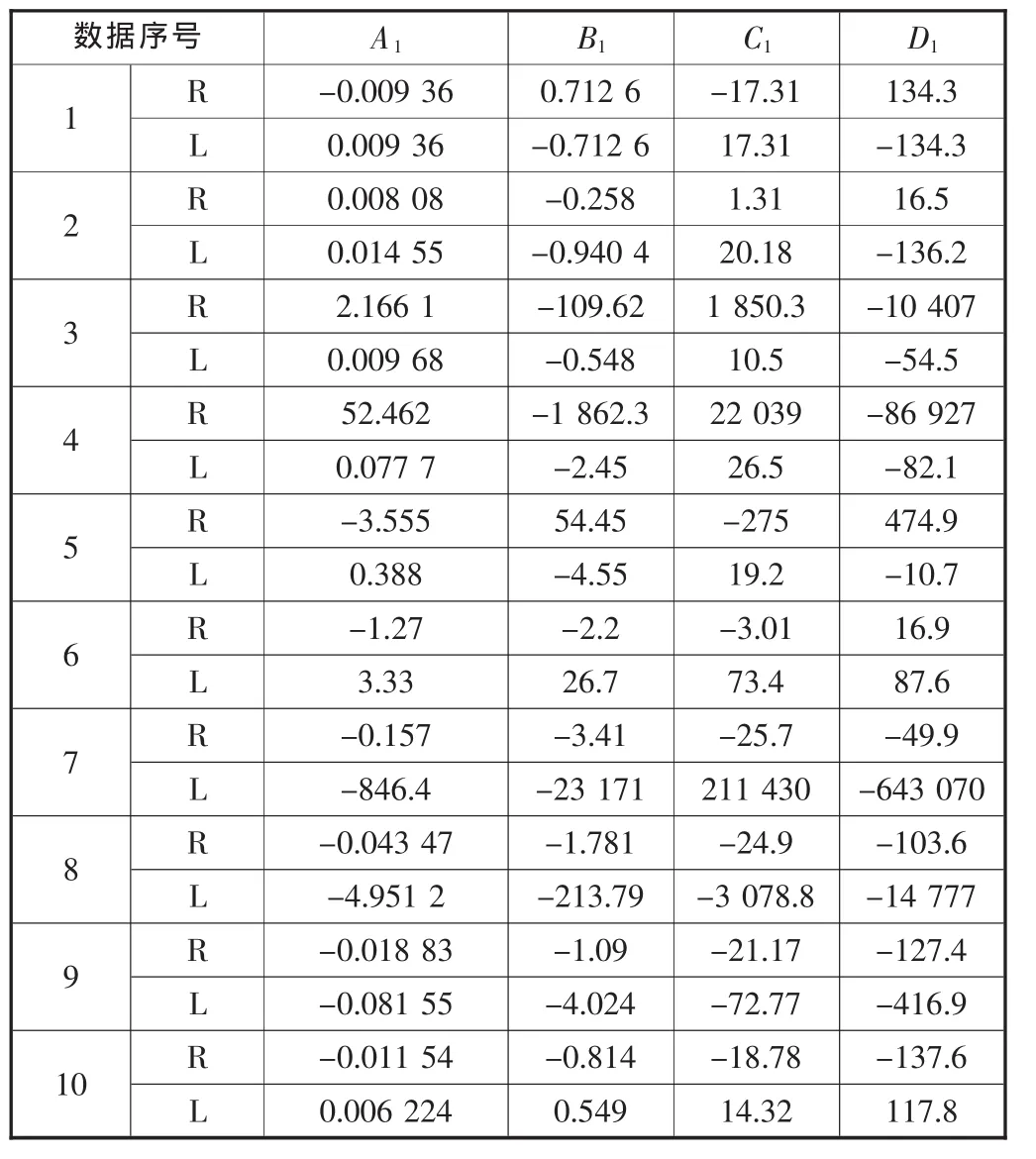
表2 实例1拟合曲线的系数

▲图7 实例2椭圆齿轮折算齿形渐开线
▲图8 椭圆齿轮三维模型

式中:A1、B1、C1、D1为 20 维的列向量矩阵数据,见表 2,表中1~10为图5中轮齿序号,R、L为其对应齿的左右齿廓。
实例2:当各参数为椭圆长半轴a=30 mm、短半轴b=24 mm、偏心率 e=0.6、模数 m=2 mm、齿数 z=28时,由对称性知只须绘制8个齿形即可,其顺序如图7所示,用上述拟合方法得到三次拟合曲线方程为:

图中,1~8为折算齿形法生成的齿廓,9为三阶椭圆齿轮齿根曲线,10为节曲线,11为齿顶曲线,A2、B2、C2、D2为20维的列向量矩阵数据,见表3。表中1~8为图7中轮齿序号,R、L为其对应齿的左右齿廓。
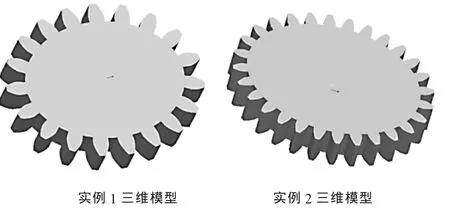
在Pro/E中通过调节渐开线与拟合曲线的曲率,使两者的曲线曲率能平滑过渡,得到的椭圆齿轮三维模型如图8所示。

表3 实例2拟合曲线的系数
4 结论
(1)通过作图与计算得到,当折算齿数大于41时,非圆齿轮的齿廓皆为渐开线。
(2)提出了用折算齿形渐开线的点来拟合齿根过渡曲线,并做了验证。通过作图得知:有的齿根曲线的拟合即使用上述三次曲线方程也得不到满意的结果,但有时轮齿左右齿廓的拟合曲线中有一条是较为合理的,这时可通过曲率半径的镜像得到另一条拟合曲线,从而代替不理想的拟合曲线。用这种方法来获取齿根过渡曲线计算量比较大,拟合曲线较复杂。
(3)通过其曲线曲率来控制,使拟合曲线与折算后的渐开线能平滑过渡,消除齿廓曲线的奇点比较复杂费时。
(4) 这种拟合过渡曲线的方法可用于高阶椭圆齿根过渡曲线的生成。
(5)齿廓曲线方程给线切割加工的编程能有所指导。
[1] 李华敏,李瑰贤.齿轮机构设计与应用[M].北京:机械工业出版社,2007.
[2] 武传宇,金玉珍,贺磊盈.基于包络特征的非圆齿轮齿廓计算方法研究[J].中国机械工程,2008,19(15):1796-1799.
[3] 史勇.非圆齿轮加工法研究及斜齿非圆齿轮滚齿加工过程仿真[D].上海:东华大学,2013.
[4] 胡赤兵,姚洪辉.基于MATLAB及Pro/E的参数化非圆齿轮设计[J].机械传动,2010,34(7):33-35.
[5] 贺敬良,吴序堂,李建刚.变性椭圆齿轮连杆机构的运动特性及齿轮副设计[J].机械工程学报,2004,40(1):62-65.
[6] 贺敬良,李建刚,王准,等.非圆齿轮的成形砂轮展成磨削原理[J].农业机械学报,2007,38(10):145-149.
[7] 吴序堂,王贵海.非圆齿轮及非匀速比传动[M].北京:机械工业出版社,1997:40-42.
[8] 李福生编译.非圆齿轮[M].北京:机械工业出版社,1975:49-58.
[9] 姚文席.非圆齿轮设计[M].北京:机械工业出版社,2013:71-73.
[10]磨齿工作原理编写组.磨齿工作原理[M].北京:机械工业出版社,1975:10-11.
