螺旋锥齿轮制造技术对比研究及应用

□ 李党育

河南西峡县内燃机进排气管有限责任公司 河南西峡 474500

螺旋锥齿轮（弧齿锥齿轮和准双曲面齿轮）是机械传动的基础零件,用于传递两相交或交错轴间的运动,具有重叠系数大、噪声小、承载能力高的优点，广泛应用于汽车、飞机、机床等高精、高速及矿山机械等重载设备。螺旋锥齿轮的设计、制造质量直接影响产品的工作性能，齿轮在传动运行中需要良好的齿形精度和啮合质量，这主要是通过切齿参数的调整来实现。由于螺旋锥齿轮在几何上的高度复杂性，要获得期望的切齿参数是很困难的，需要复杂的齿轮啮合和加工理论及相应的计算机辅助设计程序。

螺旋锥齿轮啮合和加工理论有局部共轭理论、局部综合法和三阶接触分析理论3种，他们的计算机程序应用分别以美国Gleason公司的CAGE 4Win程序、重庆理工大学郭晓冬教授的GSHgears程序、北京交通大学王小椿教授的Hyspiral程序为代表。本文分析了局部共轭理论、局部综合法、三阶接触分析等加工理论之间的差异点，并通过 CAGE 4Win、GSHgears、Hyspiral计算机程序对齿轮加工理论进行验证。

1 理论基础

1.1 Gleason局部共轭理论

Gleason技术是利用二阶齿面展成原理在齿轮副节点处形成局部共轭接触的条件来计算切齿调整参数的。局部共轭就是把小轮理论齿面修成一个与理论齿面相切而又能加工出来的实际齿面，此时将小轮实际齿面与大轮齿面相啮合，接触区不再布满整个齿面，而是形成一个以切点为中心的局部接触区，其主要思路如下。

（1）确定齿面计算点（接触区中心位置）。Gleason技术利用等距共轭曲面原理，将计算点确定在工艺节锥大轮的齿槽中点。

（2）根据接触区中心位置和选定的大轮刀具，计算大轮加工的调整参数。加工调整参数是根据保证轮副在计算点处的螺旋角、压力角以及共轭传动的充分条件求得。

（3）由大轮加工调整参数，可唯一确定大轮齿面，根据产形轮和大轮在切削中的线接触条件，可计算得到大轮齿面接触区中心的二阶几何参数。

（4）用齿轮副的共轭接触特性计算小轮齿面计算点的二阶几何参数，然后根据设计对接触区大小的要求，利用相切曲面的相对曲率原理对小轮齿面计算点的二阶几何参数进行修正。

（5）根据小轮切削时产形轮与小轮的线接触条件，确定小轮产形轮参数与小轮的相对位置，可以计算满足小轮计算点二阶几何参数要求的机床和刀具参数。

（6）用齿面接触分析法（TCA分析法）逐点计算出齿面上各接触点的位置和轨迹以及接触点处的瞬时接触椭圆的尺寸、方向和瞬时传动比等，在此过程中观察齿面的三阶接触质量情况，如果接触有缺陷，可适当改变切齿调整参数，重新计算，直到符合设计者的要求为止。

由上所述，Gleason切齿计算技术不能任意指定接触区中心的位置 ，不能准确地控制接触区的方向、大小和齿轮副的运动精度，小轮齿面控制参数多，不易操作使用，计算结果在很大程度上取决于设计者的经验和技术水平。

1.2 局部综合法

局部综合法的特点是首先确定出齿面计算点的位置（一阶接触参数）及计算点附近接触区长度、接触区方向和相对运动角加速度（二阶接触参数），这些啮合条件决定了接触区的位置与宽度、方向、传动误差的形状与幅值等传动质量，然后利用微分几何理论，推导出小轮齿面在计算点处的二阶几何参数，由此通过一次计算就可得到完全满足上述啮合条件的切齿参数。其主要思路与Gleason局部共轭理论的区别点如下所述。

（1）齿面计算点可以设定在齿面上任意的位置。

（2）预先规定啮合要求。接触区长度、接触区方向和相对运动角加速度，这些啮合要求可以全面确定齿轮副的传动质量。

（3）在确定大轮齿面接触区中心处二阶几何参数后，由齿轮副的共轭接触特性和预先规定的啮合条件直接算出小轮齿面在计算点处的二阶几何参数，而不是采取小轮齿面计算点的二阶几何参数修正的方法。

1.3 三阶接触分析理论

借助于局部综合法，可以利用二阶接触参数有效地预控齿面在计算点处及其附近的啮合性能，理论上由于齿面的光滑性和连续性，一般情况下在整个啮合区域都可保持要求的啮合性能，但是由于局部综合法对于三阶接触参数的设定与实际不符，因此在误差和变形较大的情况下，接触区可能出现接触迹线严重弯曲，瞬时接触椭圆长轴的长度变化剧烈等现象,这是由于齿面三阶以及更高阶接触参数的变化所引起的，此时就需要进一步进行三阶接触分析。

三阶接触分析理论可以通过自由选择部分机床调整参数来优化齿轮副的三阶接触参数，并以此来实现在整个传动过程中都有较好的接触性能，其主要思路与局部综合法的区别点如下所述。

（1）在计算得到大轮齿面接触区中心处的二阶几何参数的同时，计算大轮齿面的三阶几何参数。

（2）在计算出小轮齿面计算点处的二阶几何参数后，计算满足小轮计算点二阶几何参数要求的全部机床和刀具参数，同时计算小轮齿面的三阶几何参数。事实上，切齿机床上能够选择的机床调整参数的个数超过满足二阶几何参数所需要的个数，所以可以预先自由选择几个机床调整参数 （譬如变性机构或刀倾机构的参数），然后求得其余的机床调整参数。有了全部的机床调整参数之后，便可求得小轮齿面的三阶几何参数。自由选择的机床调整参数的改变不会影响齿面的二阶几何参数，只改变其三阶几何参数。

（3）齿面三阶接触特性分析。大、小轮齿面的二阶、三阶几何参数都已求得之后，就可以计算齿轮副的三阶接触特性。 齿轮副的三阶接触特性分为两大类，第一类为计算点处的二阶接触特性相对于小轮角速度或接触区弧长的变化率，它们直接影响齿轮副在理论安装距下的传动质量；第二类为齿轮副的二阶接触特性在V/H检验时对接触区中心沿大轮齿面齿长方向移动距离的变化率，它们表示了齿轮副传动特性对于加工、装配误差及受载变形的敏感性，V/H为垂直与水平位移值，mm。

（4）三阶接触特性的优化综合。将三阶接触特性参数与期望值结合设定目标函数，利用自由选择的机床调整参数的设置，优化计算小轮机床调整参数、小轮齿面的三阶几何参数以及齿轮副的三阶啮合特性。在优化过程中，大轮的齿面参数及小轮齿面的二阶几何参数是不变的，这样就有可能在保证二阶接触的同时，通过优选自由选择的机床调整参数而对三阶接触参数进行优化，以获得理想的三阶接触质量。

2 程序应用

举例对 CAGE、GSHgears、Hyspiral程序进行应用对比分析，通过计算机程序的应用对比，加深对螺旋锥齿轮加工理论的理解。CAGE 4Win、GSHgears、Hyspiral程序的主要设计计算功能见表1。

表1 软件功能表

应当注意的是表1中CAGE 4Win功能似乎不是很强大，譬如不能进行基于测量误差的切齿调整参数自动修正、没有FEA分析等，但是CAGE 4Win仅仅只是Gleason公司圆锥齿轮制造专家系统 （GEMS系统）的一个组成部分，GEMS系统是基于计算机网络的一体化制造系统，结合Gleason公司的Phoenix凤凰设备及齿轮测量系统，GEMS系统创造了一个真正的闭环设计和齿面修正的工艺系统，通常该闭环修正系统只需两次迭代就能优化齿面修正过程，功能异常强大。

文中例子采用目前汽车行业大批量生产的准双曲面齿轮，大轮采用成型法拉齿加工，小轮采用带刀倾机构刀倾法加工，亦即采用HFT法设计、加工。首先采用CAGE程序进行齿轮尺寸参数设计，然后以CAGE的计算结果作为已有设计，利用GSHgears、Hyspiral程序同样进行齿轮尺寸参数设计，验证程序的设计精度，结果见表2。

表2 齿轮参数表

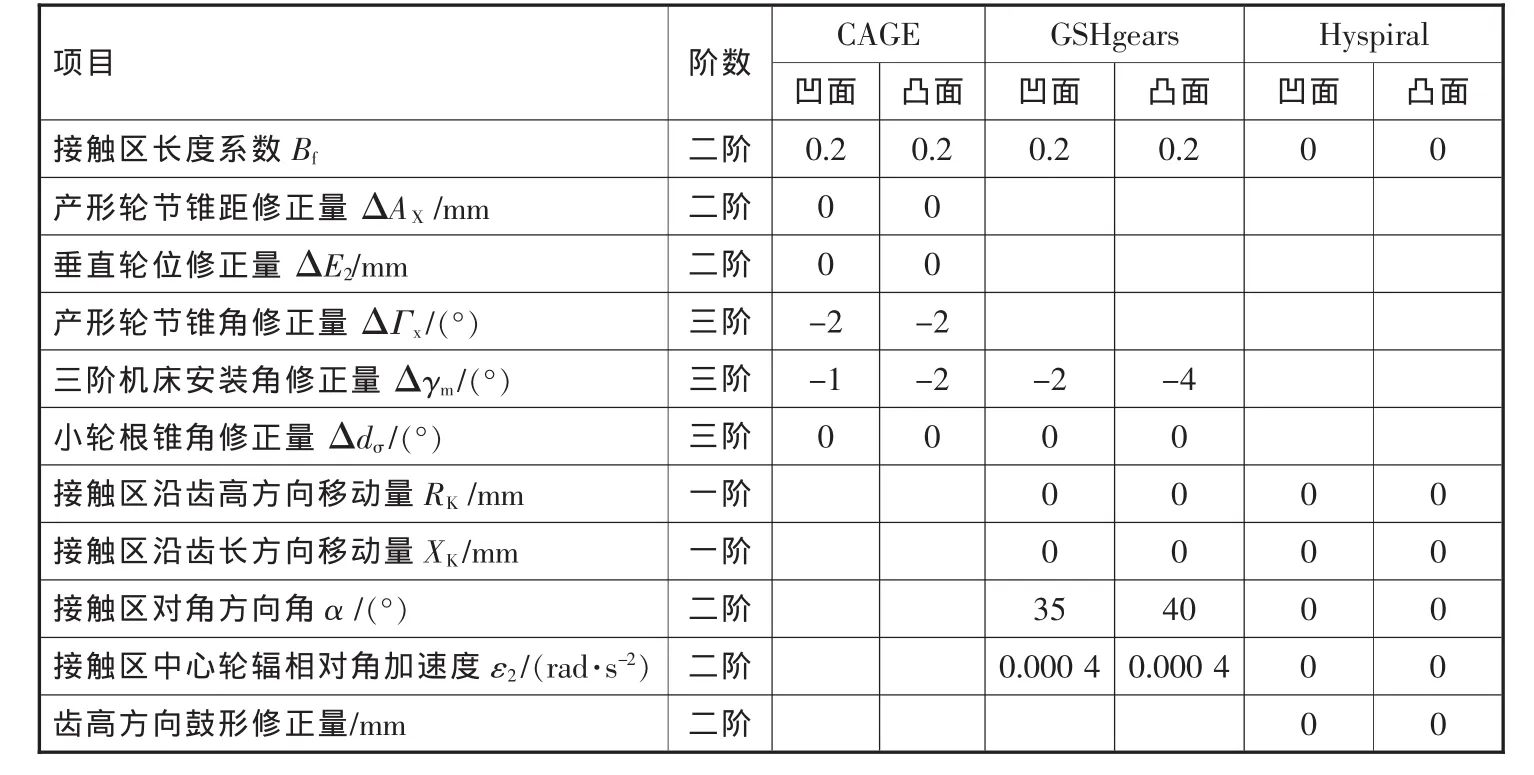
表3 小轮控制参数表

表2中带*的数据为程序在已有设计的情况下需要输入的齿轮参数（CAGE要求输入齿顶角、齿根角，可以由节锥角、面锥角、根锥角计算而得）。为了便于对比，表2中CAGE程序的数据全部是全新设计数据，而GSHgears、Hyspiral带 * 的 数 据是以CAGE的计算结果作为已有设计输入的数据，由此可以了解程序在已有设计的情况下各自需要输入什么参数。表中的带下划线数据是 GSHgears、Hyspiral程序计算结果与CAGE存在一定误差的数据，由此可以了解程序的计算误差。

其次利用程序进行齿轮加工计算，计算过程中，小轮的计算控制参数见表3。为了验证程序对设计者的经验要求，小轮控制参数仅对CAGE 4Win、GSHgears的接触区长度系数Bf进行调整，而GSHgears的TCA分析由程序自动完成，所以小轮控制参数初值均为0。Hyspiral、CAGE、GSHgears程序的TCA计算结果分别见图1、图2、图3，TCA分析计算V/H值结果见表4。

由表3可以看到，CAGE和GSHgears程序的小轮计算控制参数中有二阶和三阶控制参数，这就需要设计者具有丰富的经验，根据观察TCA图形接触区大小、形状、方向和运动曲线，配合V/H值确定符合要求的TCA分析结果。但相对于CAGE程序，GSHgears程序的三阶控制参数要少，相对容易掌握。Hyspiral程序仅有二阶控制参数，三阶控制参数由程序自动优化完成，对设计者的要求就不是太高了，当然，对程序优化的结果不满意时，也可以通过小轮控制数据进行重新计算。

TCA分析均设置在计算点和距大、小端1/4齿面宽处。由TCA分析结果可以看出，Hyspiral程序TCA分析结果非常方便，由程序自动完成优化，TCA图形、运动曲线、V/H分析值也几近完美。而CAGE、GSHgears由于没有进行多次调整，出现了诸如运动曲线不重叠不相交，产生边缘接触，GSHgears倒车面产生了鱼尾形接触等许多不良状况。如果要指导生产加工，那么应该重新调整小轮控制参数，进行再次计算修正。

▲图1 Hyspiral程序TCA分析结果

▲图2 CAGE程序TCA分析结果

表4 TCA分析V/H值计算结果/mm

TCA分析完成，机床调整参数同时计算完成。在实际生产中，根据现场调整经验，Hyspiral程序计算的切齿调整数据，在调整接触区的过程中，一般经过较少次数的调整，即可获得满意的接触区，而CAGE、GSHgears程序计算的切齿调整数据需要较多次数的调整才可获得满意的接触区，这与设计者的计算经验有一定的关系。

▲图3 GSHgears程序TCA分析结果

3 结束语

本文针对螺旋锥齿轮制造加工理论进行研究，分析了局部共轭理论、局部综合法、三阶接触分析等加工理论之间的差异点。局部综合法解决了螺旋锥齿轮切齿计算的繁琐和困难，且大大减少了所需的切齿试验次数。三阶接触分析理论在局部综合法的基础上通过设计变性机构或刀倾机构的参数，可以改善接触区形状以及二阶啮合特性对于啮合区移位的敏感性，可以自动完成比较满意的接触区计算。通过CAGE 4Win、GSHgears、Hyspiral计算机程序应用对比分析，对齿轮加工理论进行验证，有助于螺旋锥齿轮加工新技术的推广应用，提高螺旋锥齿轮设计和加工质量。

［1］ 曾韬．螺旋锥齿轮设计与加工［M］．哈尔滨：哈尔滨工业大学出版社，1989．

［2］ 郭晓东,郑昌启,林超．锥齿轮设计制造现代应用技术的研究［J］ ．重庆大学学报,1993，16（1）:37-44 ．

［3］ 王小椿,吴序堂．弧齿锥齿轮和双曲线齿轮的三阶接触分析和优化切齿计算［J］ ．齿轮,1989,13（2）:1-10 ．

［4］ 李党育，刘立新．准双曲面齿轮优化参数设计研究［J］．机械制造，1999（7）:15-17 ．