谐振式集成光学陀螺解调特性分析

郭丽君，宁 亮，孔 梅，陈拓源

(长春理工大学理学院，吉林长春130022)

1 引言

全球定位系统(Global Positioning System，GPS)/惯性组合导航技术是目前最先进、全天候、自主式制导技术。它建立在基于光学Sagnac效应的新型光学陀螺基础上。光学陀螺具有小型化、高精度、高可靠性、高寿命等众多优点［1］，有效克服了传统惯性导航精度随时间变差、难以小型化等困难。

光学陀螺是一种惯导器件，其应用非常广泛，如飞机、导弹、舰船、车辆的导航、雷达的方位测量和控制等需精确确定角度坐标的情况。光学技术的进步推动了光学陀螺的发展，激光陀螺(RLG)和光纤陀螺(FOG)的出现极大地满足了上述需求，同时，集成光学技术的发展也使微型光学陀螺(MOG)的研制成为可能。微型光学陀螺是光纤陀螺和激光陀螺的进一步小型化［1］、集成化。与激光陀螺相比，微型光学陀螺解决了闭锁问题［2］;与干涉式光纤陀螺相比，在达到同样灵敏度的情况下，它需要的波导长度要短得多。

光学陀螺可分为三类:激光陀螺、光纤陀螺和集成光学陀螺。目前，激光陀螺和干涉式光纤陀螺已经商品化，但激光陀螺存在闭锁问题［2-3］，干涉式光纤陀螺要达到高精度需要上千米的光纤。基于谐振原理的谐振式光纤陀螺仅需十多米的光纤或十多厘米的波导就能达到与上千米的干涉式光纤陀螺同样的精度，而谐振式光纤陀螺分为两种:一种是全光纤式，另一种是谐振式集成光学陀螺，相比于全光纤的谐振式光纤陀螺，谐振式集成光学陀螺更利于系统的集成化和一体化，同时，它可以采用成熟的半导体工艺制作，能够大批量生产，有利于降低成本。谐振式集成光学陀螺的种种技术优势，使其成为新一代惯性传感器件的发展方向［4-7］。

在20世纪80和90年代，美日等国开展了一系列谐振式集成光学陀螺的原理研究，微机械陀螺的出现一度阻碍了光学陀螺的研究，由于机械陀螺的精度不高，近年来谐振式集成光学陀螺得到了国内外学者的重视。目前，基于硅基光波导的谐振式集成光学陀螺研究较多，调制方案多采用LiNbO3相位调制技术［8-10］，由于调相检测方式引入了不同于硅基光波导材料的LiNbO3相位调制器，不利于陀螺的集成化，而小型化、集成化是谐振式集成光学陀螺的发展趋势，最终目标是把激光器、声光移频器、谐振器集成到一片硅基芯片上，因此可集成于硅基光波导的激光频率调频检测是比较理想的一种检测技术［11-12］。本文利用贝塞尔函数展开和光波场叠加的方法分析了谐振式集成光学陀螺在激光频率调制光谱技术下调频检测系统解调输出信号与谐振频率偏差之间的关系。根据解调输出信号的解析表达式，通过数值计算，分析了解调曲线的变化规律，得到了施加在激光器压电陶瓷(PZT)驱动器上调制波形的最佳调制系数，并在实验上得到解调曲线。

2 谐振式集成光学陀螺的信号检测

谐振式集成光学陀螺的基本结构如图1所示，从光源S发出的相干光由3 dB耦合器C1分成两束，然后借助于耦合器C2沿着相反方向注入谐振腔中。谐振腔中逆时针光波的谐振频率，通过耦合器C4由探测器D1检测，顺时针光波的谐振频率，通过耦合器C3由探测器D2检测。在没有旋转的情况下，逆时针和顺时针的谐振频率是相同的，当环形谐振腔以角速度Ω旋转时，两束反向传播的的谐振光波产生一个谐振频差［13］:

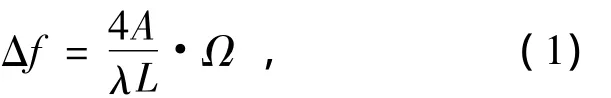
式中:A为谐振腔包围的面积;L为 腔长。4A/λL为谐振式集成光学陀螺的标度因子，只要检测出Δf，就可以确定旋转角速度Ω。

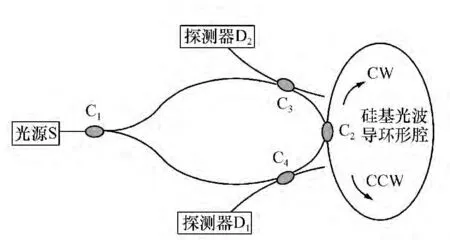
图1 谐振式集成光学陀螺的基本结构框架图Fig.1 Basic framework of R-IOG

谐振式集成光学陀螺不同于干涉型光纤陀螺，它不宜采用全开环的调制解调方式而必须采用锁定某一个方向传播的光波，使其处于谐振状态。通过间接探测另一方向传播的光波与它的频率差来得到旋转角速度。对于图1中的结构，环形谐振腔采用硅基二氧化硅环形谐振腔结构，由2个输入/输出3 dB耦合器、1个环形腔耦合器(耦合系数为0.1)构成，在谐振腔中沿逆时针方向传播的光的谐振频率，通过耦合器C4由探测器D1检测，可以用输出曲线上所观察到的谐振峰将激光器的光频率锁定在逆时针方向的腔谐振的中心频率上，锁定技术如图2所示，通过在fm上对激光器进行频率调制和在声光解调器中对D1的输出进行解调，输出为零对应的光频率为逆时针方向的腔的频率，由此利用伺服回路来锁定光源的光波频率。同理，沿顺时针方向传播的光通过耦合器C3由探测器D2检测，并在第二个声光解调器中解调。通过与光源的光波频率进行比较，这个解调器输出给出了旋转的幅值和方向。这就是谐振式集成光学陀螺的开环检测原理。

3 光器件的传输特性

光波在谐振式集成光学陀螺系统中传播所经过的光学器件主要包括激光器、声光晶体移频器、光波导环形谐振器、探测器。按照光的传输方向，讨论光波经过上述器件后最终在探测器得到的波形变化情况。

3.1 激光器频率调制光谱技术

在图2所示结构中，设激光载波电场强度为:

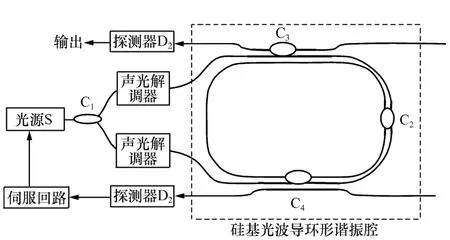
图2 谐振式集成光学陀螺开环检测原理Fig.2 Principle of open loop detection for resonator integrated optical gyro

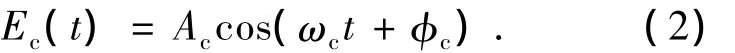
如果调制信号是一个时间的正弦函数，可写成:

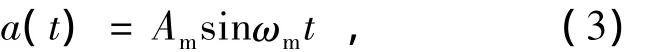
式中，Am和ωm分别是调制信号的振幅和角频率。

通过PZT对光源进行调制，并进行贝塞尔函数展开，得到激光器的输出为:

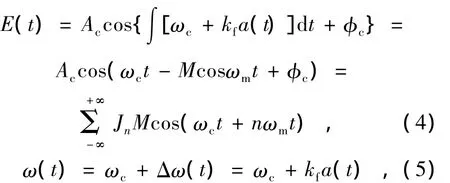
式中，Jn为第一类贝塞尔函数，M为调频系数，

3.2 声光移频器技术

结合式(4)，经过声光移频器后的输出可写成:

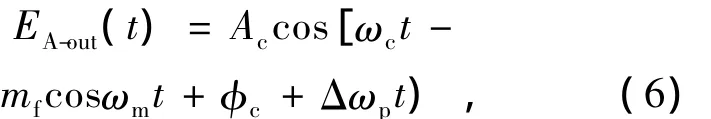
式中，Δωp=2πΔfp，Δfp为声光移频器的移频量。令 fc=f0－Δf+Δfp，ωc=2πfc，上式改写为:

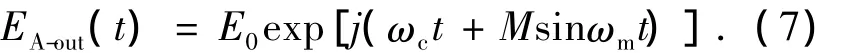
3.3 环形谐振腔技术

谐振腔对输入输出的影响可以写成频域内传递函数的形式:

看得出，老陈有些激动，他甚至握住了我的手，说小马啊，咱爷俩认识这么久了，还从没在一起喝喝呢。也不管我乐不乐意，老陈拽了我，叫我去他家。进了门，我才知道他已备好菜了，四个小菜，一瓶酒。我想老陈的意思肯定是因为打电话举报我向我道歉的。我坐下后，老陈倒上酒，说别的话就不说了，我先干为敬。

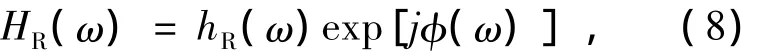
式中，HR(ω)为谐振腔传递函数的幅值部分，φ(ω)为相位延迟部分。

对于反射式谐振腔，根据耦合模理论，谐振腔的输出与输入光强之间的关系有［14］:

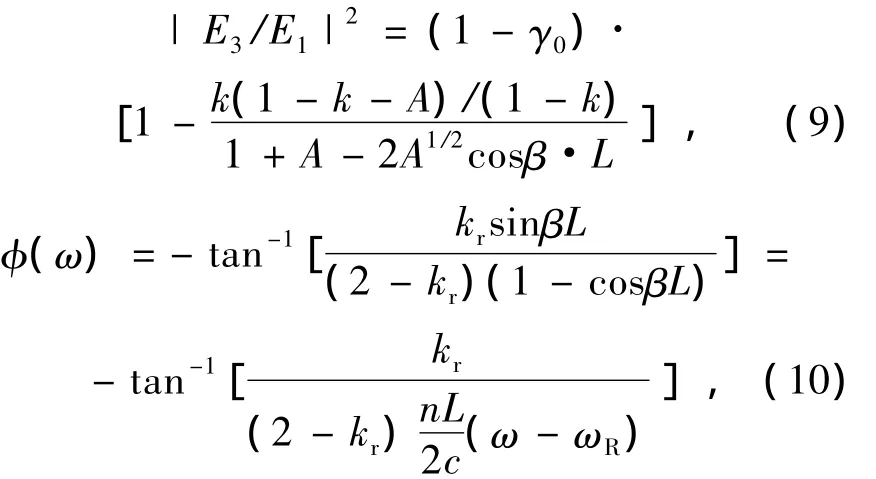
式中，α为波导的单位长度损耗，γ0环形耦合器的插入损耗，k为耦合器的光强耦合系数，kr为最优化光强耦合系数。

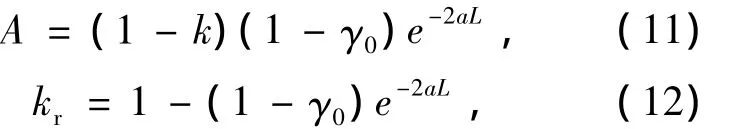
采用洛伦兹公式来描述谐振腔传递函数:

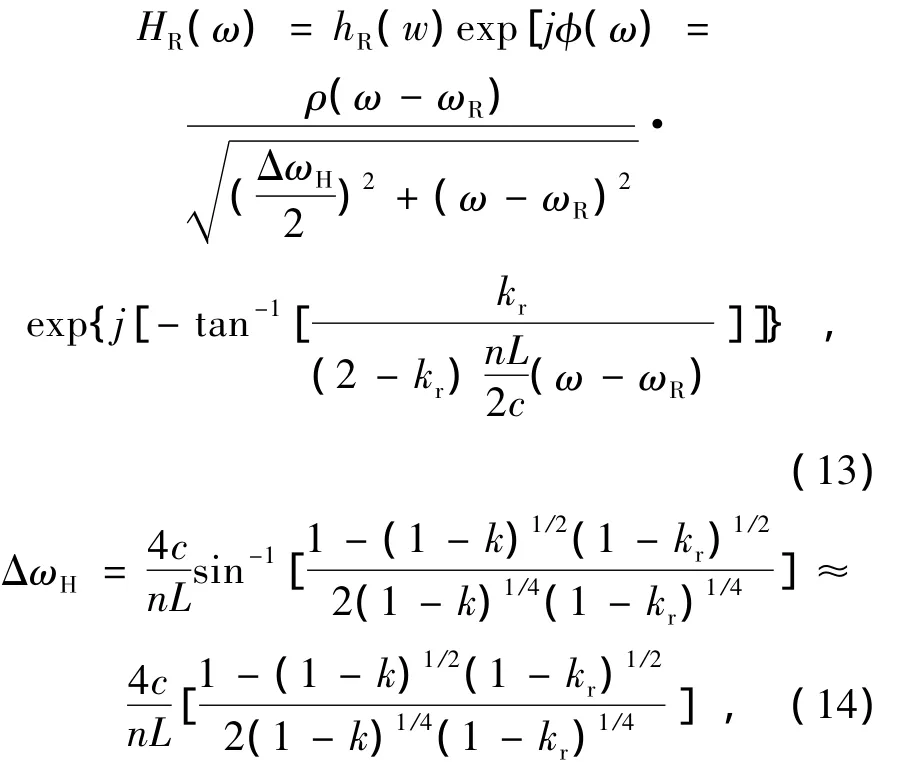
式中，ρ为谐振腔的谐振深度，ωR为谐振腔的谐振角频率，ω为谐振腔输入光的角频率。

则谐振腔输出为:

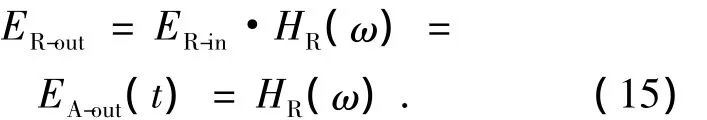
把上式用贝赛尔函数展开，令ωn=ωc+nωm，

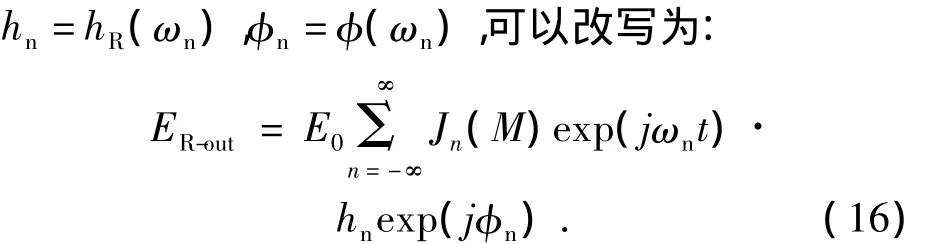
3.4 光电探测器技术

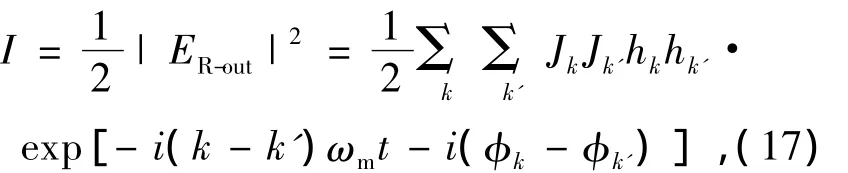
由于解调是利用一次谐波完成，因此上式只考虑k－k'=±1项。

由贝塞尔函数Jk(x)的性质可知，只要考虑k=0、±1即可，则:

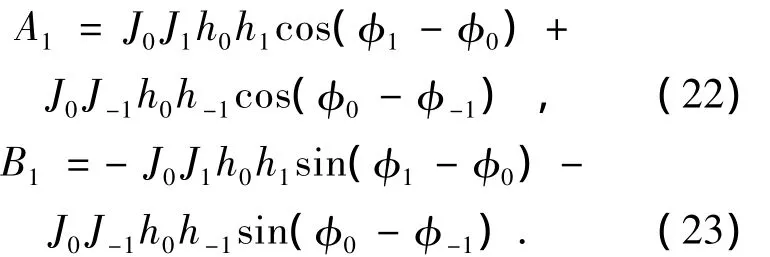
4 解调特性仿真与实验研究

4.1 解调特性仿真

在信号解调时用的是sinωm，利用正交锁相法将正弦项sinωm提出，则输出电压与频移的关系就用B1项表示。将环形谐振腔传递函数的具

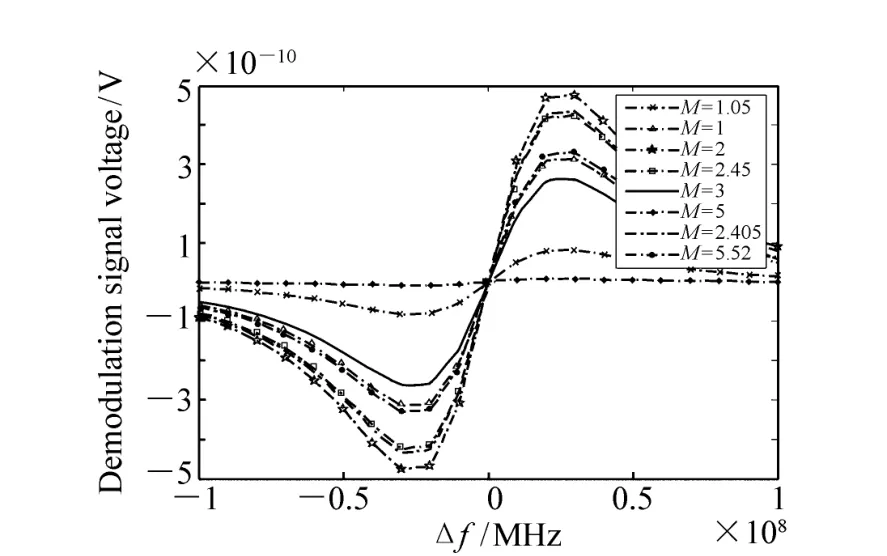
图3 解调曲线波形(k=0.1;α =0.02;L=0.04;c=3 ×108;n=1.45;fm=1 000 Hz)Fig.3 Waveforms of demodulation curve

体公式和贝塞尔函数带入B1中，就可以得到图3。由图3可知，在谐振点(Δf=0)附近，有一段较长的线段，这就是谐振式集成光学陀螺的线性工作区间，解调曲线具有很好的线性。在不同的调制系数下，谐振式集成光学陀螺的线性工作区范围、解调曲线的形状是不同的。优化设计的关键就是寻找最佳的调制系数，使解调曲线在谐振式集成光学陀螺线性工作区间的斜率最大，从而提高检测系统的响应灵敏度。通过数值模拟，当M=2时，线性工作区间斜率最大，解调曲线最好。

4.2 解调曲线测试

图4为基于激光频率调制解调测试框图。在R-谐振式集成光学陀螺解调实验中，测试所用的光源为中心波长为1 550 nm，线宽为50 kHz的光纤激光器，其输出波长(或频率)可通过外加电压进行调制。利用锯齿波发生器产生锯齿波，驱动光纤激光器内部的PZT对激光器输出光频率进行扫描，信号发生器提供的1 Hz三角波信号与1 kHz的调制正弦信号通过加法器(Adder)相加，通过PZT驱动器进行光放大，进而得到解调曲线，解调曲线如图5下半部分所示，由图可知，解调输出曲线的形状与图3相似。由于环形腔的偏振效应，从图4可观察到两类不同的解调曲线。信号较强、移动较慢的信号是由SiO2光波导的慢轴产生的，这是有用信号，另一个则对应于快轴，属于干扰信号。根据图5解调曲线，解调曲线的线性部分的振幅为5.04 V，对应的时间间隔为22 ms，FL工作频率的变化值与外加电压之间呈线性变化，变化率为18.73 MHz/V，因此FL的输出频率偏移随时间的变化关系为3 221.56 MHz/s，频率在较深的解调曲线的线性部分是 ±35.44 MHz。标度因子为17.72×103Hz/(rad/s)时，谐振式集成光学陀螺的动态范围为±2.0×103rad/s。这个结果与目前大多数采用的LiNbO3相位调制技术所得的结果在同一个数量级上［15］。

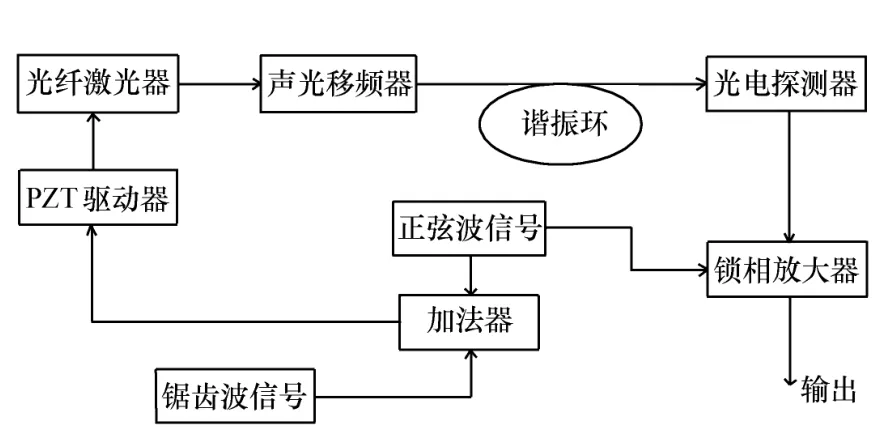
图4 调制解调测试框图Fig.4 Test Block Diagram of modulation demodulation

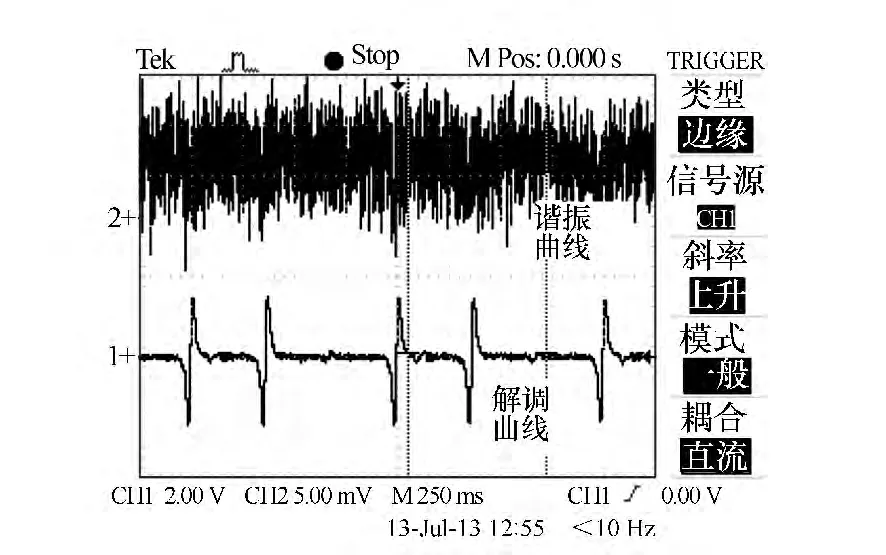
图5 实测的解调曲线Fig.5 Demodulation curve of test

5 结论

本文提出了一种基于激光器频率调制谱检测方案，通过理论分析、数值计算和实验，分析了调频调制检测系统解调输出信号与谐振频率偏差之间的关系，得到解调曲线的变化规律;同时对调频检测方案中的主要参数进行优化，当调制系数M=2时，线性工作区间斜率最大，解调曲线最好，并在实验上得到解调曲线。数值仿真和实验结果表明，实测形状与理论分析结果相符，从解调信号得到陀螺动态范围为±2×103rad/s。为谐振式集成光学陀螺检测系统的进一步优化设计提供理论和实验依据。

［1］ 刘福民，徐宇新，金锋.微型集成光学陀螺研究进展［J］.导航与控制，2004，3(4):43-49.LIU F M，XU Y X，JIN F.Research developments of micro-optic gyroscope［J］.Navigation and Control，2004，3(4):43-49.(in Chinese)

［2］ 郭伟，金仲和，唐衍哲，等.一种新结构的硅基无源环形波导式谐振腔［J］.半导体光电，2003，4(1):29-31.GUO W，JIN ZH H，TANG Y ZH，et al..A new configuration of passive Si-based ring waveguide resonant cavity［J］.Semiconductor Optoelectronics，2003，4(1):29-31.(in Chinese)

［3］ 米剑，张春熹，李铮，等.偏光干涉对光纤陀螺性能的影响［J］.中国光学，2005，26(8):1140-1144.MI J，ZHANG CX，LI Z，et al..Effect of polarization interference on fiber optic gyro performance［J］.Acta Optica Sinica，2005，26(8):1140-1144.(in Chinese)

［4］ REN Y，JIN ZH H，CHEN Y，et al..Optimization of the resonance frequency servo loop technique in the resonator micro optic gyro［J］.Zhejiang Univ.Sci.C，2011，12(11):942-950.

［5］ ZHI Y ZH，FENG L SH，LEI M，et al..Low-delay，high-bandwidth frequency-locking loop of resonator integrated optic gyro with triangular phase modulation［J］.Appl.Optics，2013，52:8024-8031.

［6］ FENG L SH ，LEI M，LIU H L，et al..Suppression of backreflection noise in a resonator integrated optic gyro by hybrid phase-modulation technology［J］.Appl.Optics，2013，52:1668-1675.

［7］ GUO L J，SHI B R，ZHAO M，et al..Direct-coupled large-diameter silica on silicon waveguide ring resonator used in microoptic gyro［J］.International J.Optomechatronics，2011，5:30-50.

［8］ MA H L，ZHANG X L，JIN ZH H，et al..Waveguide-type optical passive ring resonator gyro using phase modulation spectroscopy technique［J］.OE Letters，2006，45(8):080506-1-080506-3.

［9］ ZHANG X L，ZHOU K J.Open-loop experiments of resonator micro-optic gyro［J］.Optoelectronics Letters，2009，5(2):97-100.

［10］ ZHANG X L，MA H L，ZHOU K J，et al..Experiments by PM spectroscopy in resonator fiber optic gyro［J］.Optical Fiber Technology，2007，13:135-138.

［11］ CARROLL R，COCCOLI C D，CARDARELLI D，et al..The passive resonator fiber optic gyro and comparison to the interferometer fiber gyro［J］.SPIE，1986，719:169-177.

［12］ IMAI T，NISHIDE K，OCHI H，et al..The passive ring resonator fiber optic gyro using modulatable highly coherent laser diode module［J］.SPIE，1991，1585:153-162.

［13］ EZEKIEL S，BALSAMO R.Passive ring resonator laser gyroscope［J］.Appl.Phys.Lett.，1977，30:478-480.

［14］ ZHANG F，JOHN W Y，et al..Direct-coupling single-mode fiber-ring resonator［J］.Optical Society America，1988，5:1347-1355.

［15］ ZHANG X L，ZHOU K J.Open-loop experiments of resonator micro-optic gyro［J］.Optoelectronics Letters，2009，5(2):97-100.