基于冷中子谱的紧凑型中子自旋倒相器设计

李新喜，王 燕，王 云，黄朝强，张 莹

(中国工程物理研究院核物理与化学研究所中子物理学重点实验室，四川绵阳621999)

1 引言

中子具有自旋磁矩，可作为无损磁性探针探测磁性材料微观结构，研究磁性材料的微观结构性质［1］。常见的极化中子散射谱仪极化系统中，极化器的功能是将入射中子束流中单一取向的中子取出来，从而实现中子束流的极化。目前的极化器通常采用多层膜极化超镜，多层膜极化超镜利用磁性薄膜材料的反射与中子自旋取向有关，对于自旋向上和向下对应有两个反射临界角，调节饱和磁化下多层磁性膜对两种自旋取向中子束流的散射势，使单一自旋取向的中子全反射，另外一种全透射。无论采用反射束或透射束作为极化中子束流，实现不同自旋取向的入射极化中子束流探针，需要高效率中子自旋倒相器实现极化中子自旋取向翻转。中子自旋倒相器基于磁共振原理［2］，通过有效场的翻转设计，实现一种自旋取向的极化中子的跃迁［3-5］。中子自旋倒相器作为中子极化系统中一个重要的中子光学组件，其翻转效率直接影响着中子散射实验的精确度。对于翻转效率不高的中子自旋翻转器，后期的实验误差修正也相当的麻烦。随着磁性材料研究的快速发展，极化中子散射物理实验精度要求越来越高，相应的对整个极化系统的整体功能以及精确性要求也越来越高。国际上中子自旋倒相技术发展很快，相应的理论研究也逐步深入［6-12］。随着极化中子散射谱仪的研究逐渐增多，中子自旋倒相器的应用也越来越广泛［13-18］。国内中子散射研究处于起步阶段，随着中子源的发展，相关研究也逐渐增多［19-22］，20世纪70年代，宽通道缓变中子自旋倒相器在俄罗斯圣彼德堡研发成功［5］，目前已经广泛应用在多个中子散射中心极化中子散射谱仪上。国际上常用的中子自旋倒相器类型有Korneev型、RF-Adiabatic型。Korneev型中子自旋倒相器的工作区域较狭窄，主要用于窄中子束流高分辨谱仪的极化系统，相应的主体结构与绝热缓变型中子自旋倒相器也有较大的差别。RFAdiabatic型中子自旋倒相器由于中子束流通道宽而得到了广泛的应用，相应的技术发展也比较快。目前绝热梯度型中子自旋倒相器的设计，通常需要先进行理论计算进行参数选定，然后再采用中子束流实验进行少量的参数优化。中子束流比较昂贵，理论优化计算在设计中是相当必要的，可避免大量的实验修正。可通过正余弦方法［5］或蒙卡模拟计算软件进行计算。正余弦模型中自旋倒相器振荡场为正弦模式，梯度场为余弦模式。由于实际的复合磁场设计中，磁场很难完全满足这两种形式，因此有相当大的计算偏差，需要进行大量的实验参数修正。蒙卡粒子跟踪模拟软件有新近更新的VITESS模拟计算软件，VITESS模拟软件计算输入相对解析方式较为复杂。多数中子自旋倒相器为独立设计，配备有独立的梯度磁场及振荡磁场产生设施。在中子散射谱仪设计中，为节省光路空间，在满足使用需求的情况下，部件设计尽可能在空间利用上高效紧凑。

2 自旋倒相器的构成及数值计算原理

2.1 紧凑型中子自旋倒相器的结构

图1为紧凑型中子自旋倒相器的结构图，主要由前端极化器静磁场、自旋倒相器高频线圈、高强度铝窗、真空系统和支架等组成。为减少中子束流损失，整个极化系统放置在真空管中。使用时，需要高频电源供电，从而中子自旋倒相器高频线圈中心产生高频磁场。充分利用极化器静磁场在短距离的衰减形成的梯度场作为后端中子自旋倒相器的引导场，无需为后端的中子自旋倒相器设计专门的梯度引导场，从而形成更为紧凑的极化系统设计。

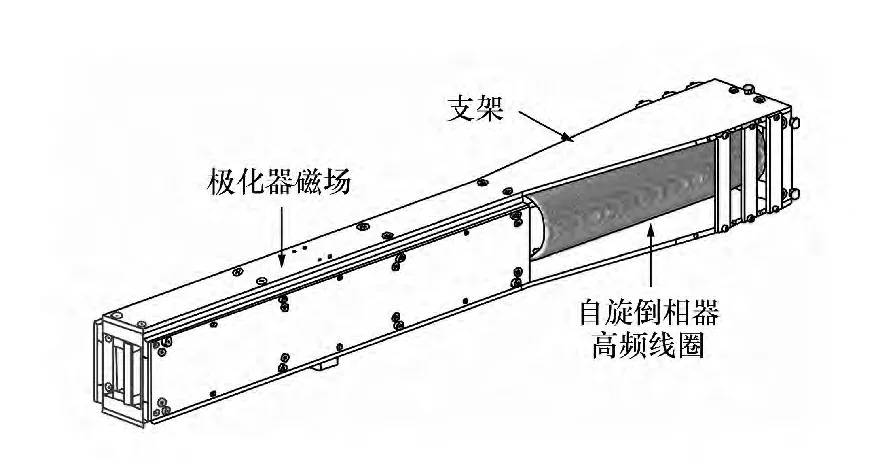
图1 紧凑型中子自旋倒相器结构Fig.1 Scheme of compact neutron spin flipper

2.2 自旋倒相器数值计算原理

从量子力学上理解，中子自旋取向在外场中是量子化的，只有平行与反平行于外磁场两种。中子的两种自旋取向是指中子磁矩具有两种本征态，当整个系统处于非本征态的任意状态时，也就是分别以一定的几率处于两个本征态。如果在系统中加一个交变磁场，微观自旋系统就会受激发生能级跃迁，从而实现中子自旋处于不同本征态的几率变化，对于单一能级中子，受激大几率跃迁实现自旋取向的翻转。缓变自旋倒相器即是利用上述基本原理，实现单一自旋取向中子在复合磁场中的自旋取向翻转。

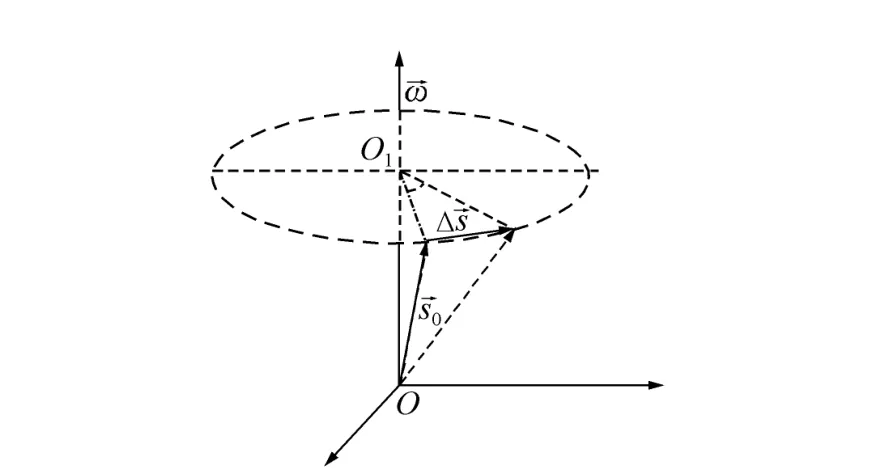
图2 中子自旋在有效磁场中的缓变示意图Fig.2 Scheme of neutron spin in effective magnetic field

中子自旋倒相器的复合磁场包含的磁场由梯度引导磁场和振荡磁场两部分构成，方向相互垂直。假定复合磁场中的中子自旋取向为矢量s，矢量s在复合磁场中的自旋取向缓变由图2很容易获得下式:

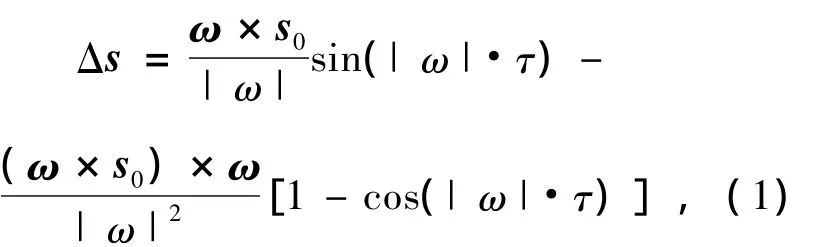
式中，s0为计算点的中子自旋投影，ω=γ·Beff为极化中子在计算点的进动频率，γ=1.83×108rad/s·T为旋磁比，Beff为单一自旋取向中子在计算点位置时感受到的有效磁场，有效磁场由振荡磁场和梯度磁场组成，τ为从计算点开始至下一个点的极化中子运动时间。

数值模拟从自旋中子进入到复合磁场开始，至自旋中子离开复合磁场结束，模拟在复合磁场整个运动的空间内沿中子束流方向的自旋取向翻转图像。

3 模拟计算与讨论

3.1 计算模型

紧凑型缓变中子自旋倒相器从结构上主要利用前端中子极化器的静磁场自然衰减，从空间上靠近前端极化器静磁场，调制中子自旋倒相器的交变场频率，在非常有限的空间下实现高效紧凑的中子自旋倒相器设计。

图3是紧凑型中子自旋倒相的复合磁场模型。极化器静磁场沿中子束流方向产生一个类指数衰减的自然下降，这个自然下降的磁场可作为中子自旋倒相器的梯度引导场，将高频交变线圈放置在梯度场上合适的位置，梯度静磁场与交变场形成中子自旋倒相器的复合磁场通道，在限定空间下，调制高频磁场线圈频率从而使极化中子通过复合磁场后实现高效率自旋取向翻转。

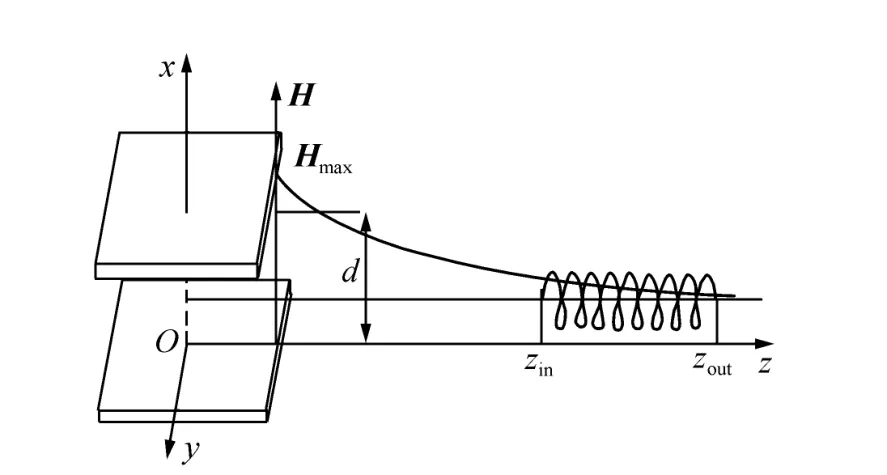
图3 紧凑型中子自旋倒相器复合磁场模型Fig.3 Synthetical magnetic field model of compact neutron spin flipper

图4给出了实际模型中极化器静磁场在后端沿束流的自然衰减实验曲线。由实验数据看出，在长度为50 cm内，静磁场自然衰减到零。中子自旋倒相器考虑选取较为平稳段作为梯度导向场，中子自旋倒相器起始端选取位置为距极化器Zin=100 mm处。

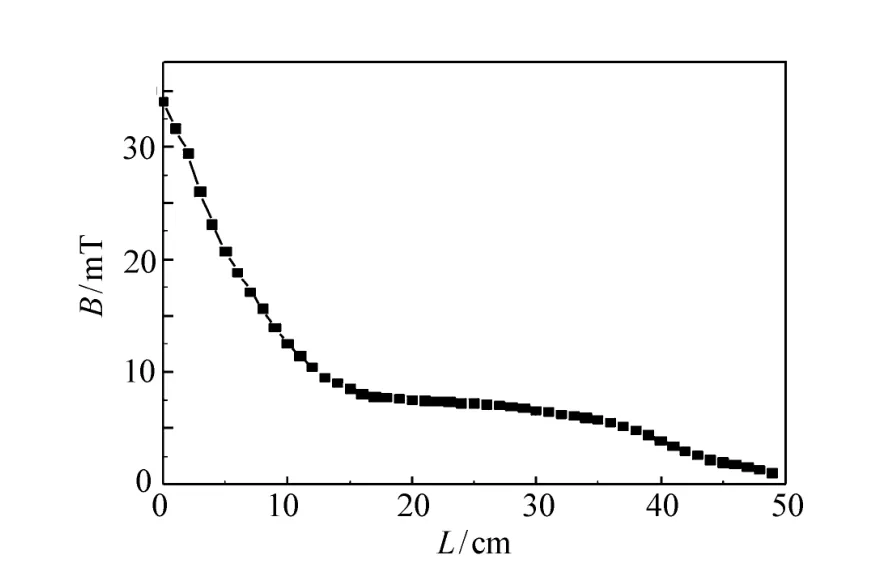
图4 梯度静磁场沿束流方向的自然衰减实验测量数据Fig.4 Spontaneous attenuation experiment data of gradient magnetic field along the neutron beam flight

3.2 振荡场频率的优化计算

中子自旋倒相器的交变磁场由高频振荡线圈提供，高频振荡线圈配有专门的高频磁场电源。在自旋倒相器设计参数中，交变场频率是较为容易调节的一个物理参数。由于通常的中子自旋倒相器设计模型比较理想，实际使用时按照设计参数中子自旋翻转效率通常会产生一定的偏差。因此，在实际使用中，中子自旋倒相器的高频磁场频率成为一个重要的修正参数。利用实际束流调制频率，可实现使用极化中子波段的高效率自旋取向翻转。对于高频电源的设计，依据中子自旋倒相器优化设计频率值，适当预留一定的频率调节空间，用于实际使用中的优化调制，同时针对可能由于静磁场的自然衰减导致的性能降低进行及时的优化，从而满足极化中子散射物理实验的需求。

设计考虑实际的冷中谱，波长为 0.25～12.5 nm。中子最小波长决定了整个波段的翻转效率，并且翻转效率与波长成正比［5］。因此，计算中只需要考虑最小波长0.25 nm即可。为实现实际设计的模型具有较高的翻转效率，模型设计中采用更小的波长0.25 nm，空间输入物理参数见表1。

表1 中子自旋倒相器物理参数Tab.1 Input parameters of neutron spin flipper(mm)

图5给出了中子自旋翻转率随交变场频率变化的计算结果。由计算结果可以看出，极化中子通过中子自旋倒相器后半段时，极化中子自旋翻转率有一个迅速的提高，达到较高的自旋翻转率后处于平稳状态。对于交变磁场的频率，达到较高自旋翻转效率有一个最佳频率约198 kHz，对于偏离198 kHz的交变频率，中子翻转效率均有下降，同时有明显的振荡。

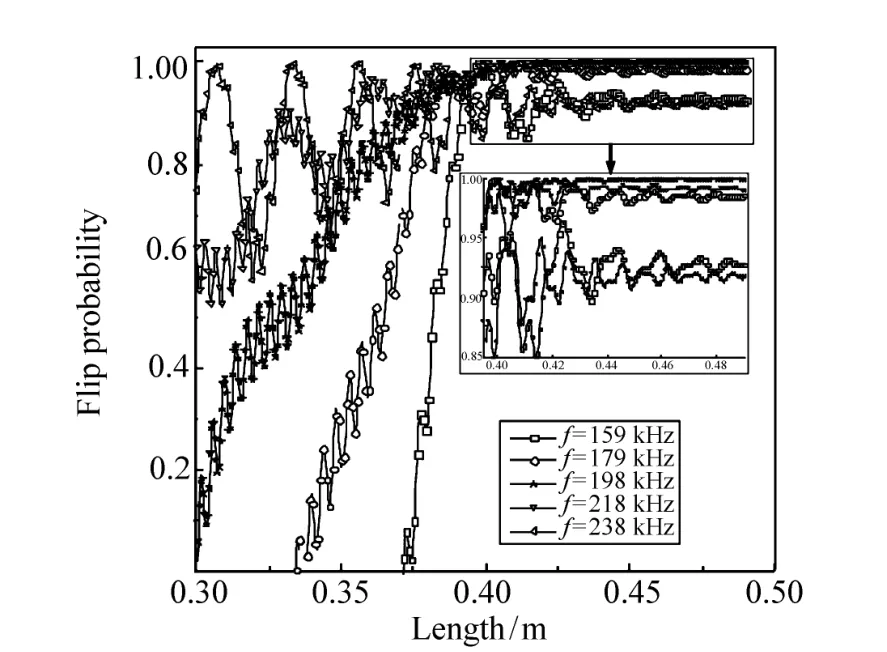
图5 自旋翻转率与交变场频率的关系计算Fig.5 Spin flip probability for different frequency of oscillating field

3.3 中子自旋倒相器翻转过程图像模拟

按照经典的处理方法，极化中子在自旋倒相器轴向空间飞行过程中是逐渐进动倒向的，翻转图像可以观察极化中子在复合匹配磁场通道中的振荡情况。

极化中子在自旋倒相器内沿飞行方向的自旋取向在初始极轴上的投影曲线见图6。由模拟计算的翻转图像投影可以看出，在整个自旋取向翻转过程中，在自旋倒相器的前半段有一些小的振荡。这可能是由自然衰减的梯度引导场的非理想梯度引起的。

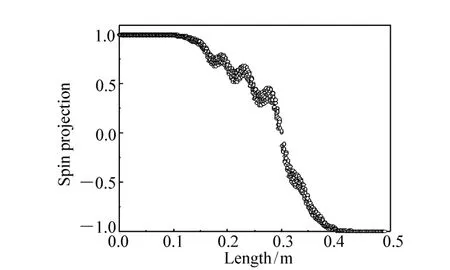
图6 中子自旋倒相器内的翻转图像投影Fig.6 Distribution of neutron spin projection in the flipper

3.4 紧凑型中子自旋倒相器翻转效率模拟

图7给出了优化频率翻转效率沿中子自旋倒相器轴向的变化曲线。由模拟计算结果可以看出，设计的紧凑型中子自旋倒相器性能良好，在中子自旋倒相器的出口相当长一段距离内，中子自旋翻转效率在99%以上，并且处于相当稳定的高翻转效率状态。

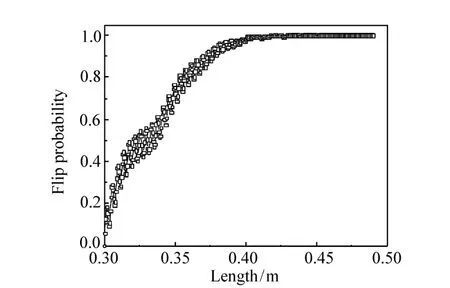
图7 翻转效率沿中子自旋倒相器轴向的变化Fig.7 Flip probability image along the axis of flipper

3.5 交流频率稳定性对效率的影响

实际使用的高频电源频率通常会有一定的波动，高效率中子自旋倒相器，需要其翻转效率具有相当高的稳定性。因此，对于中子自旋倒相器的优化设计，需要考察其对频率波动引起的翻转效率影响。

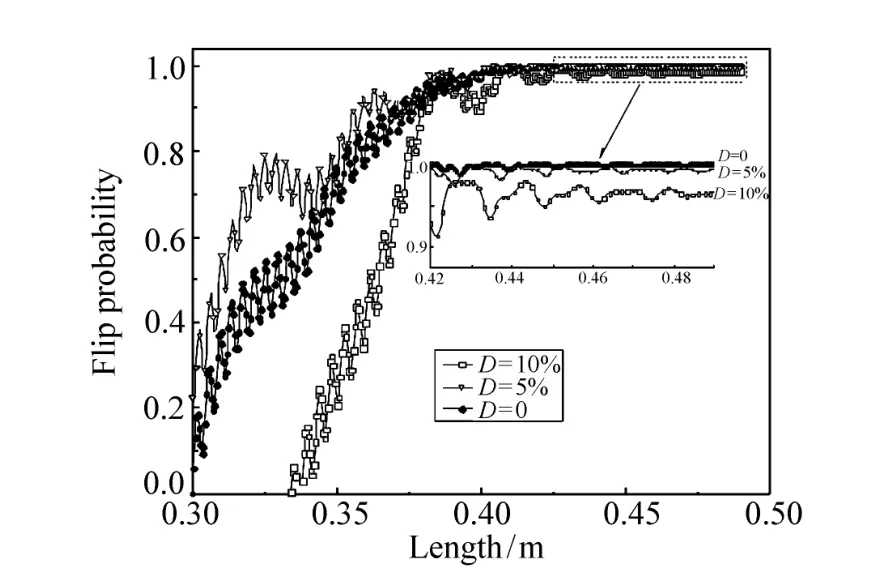
图8 交变频率对效率的稳定性影响计算Fig.8 Influence of small fluctuate frequency for flip probability

图8给出了交变频率对效率的稳定性影响曲线。计算主要考察在使用过程中交变场频率波动给翻转效率带来的影响，从而判断设计结构的效率稳定性。从计算结果来看，设计的紧凑型中子自旋倒相器的自旋翻转效率具有一定的稳定性。从放大的稳定区翻转效率来看，交变场频率偏差在5%以内，效率降低不是很大，均能在99%以上。对于频率交变场频率偏差在10%时，翻转效率有明显的下降。因此，对于交变场的电源频率设计，需要充分考虑设计高频的稳定性。

4 实验测量与结果

4.1 交变场电源的稳定性实验测量

中子自旋倒相器的交变场是密绕的螺线管提供的，设计的交变场电源电流的稳定性直接影响着交变场。螺线管轴线磁场［23］可用下式来表示:

式中，μ0为真空磁导率，n为螺线管匝数，K为螺线管空间物理参数。

实际使用中，交变场电源的频率和电流均是重要的性能调节参数。因此，其设计指标需要有较好的稳定性。

表2给出了交变场电源电流与设计值一致性的实验测试结果。由实验结果可以看出，实际测试电流偏差均在2%以内，使用电源表现出良好的性能。

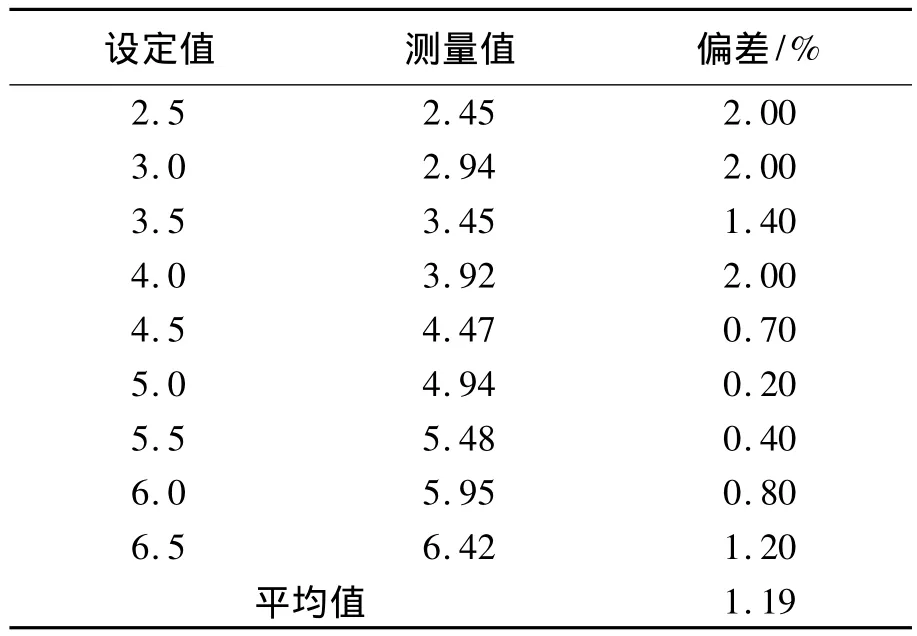
表2 振荡磁场线圈电流测试结果Tab.2 Electric current measuring results of oscillating winding (Unit:A)

4.2 中子自旋倒相器翻转效率测量

自旋翻转效率是中子自旋倒相器的重要指标参数。中子通过倒相器翻转的效率可看成单一自旋取向的中子由导向磁场方向朝导向磁场相反方向的变化几率。由于探测器探测到的仅仅是中子计数，无法区分极化中子的自旋取向。在中子自旋倒相器翻转效率的物理实验测量中，需要将待测中子自旋倒相器放置到由极化器、极化分析器、辅助中子自旋倒相器组成中子散射谱仪极化系统中。实验获得4个不同部件组合的中子束流强度分量，计算后获得中子自旋倒相器的翻转效率［5］。探测器为二维位敏探测器，入射束流采用狭缝系统进行了准直。

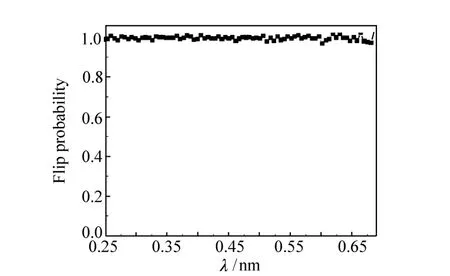
图9 翻转效率测试结果Fig.9 Measuring result of flip probability

图9给出了实验获得的紧凑型中子自旋倒相器翻转效率的实验测试结果。实验采用冷中子导管输出的强度最强的中子波段，实验曲线有些杂散信号，这可能是由于入射束流准直不够理想以及实验本底影响的结果。实验测试结果表明，设计的紧凑型中子自旋倒相器性能良好，翻转效率在99.2%以上。

5 结论

中子自旋倒相器是极化中子散射谱仪中非常重要的一个光学部件。对于极化中子散射谱仪设计，中子光路的设计空间是非常有限的，在光路上节省一定的空间，为其它中子光学部件(例如较大的环境加载设备)节省空间，同时由于中子光路基本都要处在真空环境中，空间的节省降低了成本。本文基于实际磁场模型，对中子自旋倒相器的相关物理参数进行了优化计算，考察了其稳定性，为辅助部件设计提供了理论方案。针对设计的紧凑型中子自旋倒相器，对其重要物理参数中子自旋翻转效率进行了实验测量，实验结果证明:中子自旋倒相器可与前极化器磁场形成高效紧凑型设计，翻转效率在99.2%以上。

［1］ 丁大钊，叶春堂，赵志祥.中子物理学［M］.北京:原子能出版社，2001.DING D ZH，YE CH T，ZHAO ZH X.Neutron Physics［M］.Beijing:Atom Energy Press，2001.(in Chinese).

［2］ 冯蕴深.磁共振原理［M］.北京:高等教育出版社，1992.FENG Y SH.Magnetic Resonance Principle［M］.Beijing:Higher Education Press，1992.(in Chinese)

［3］ NEWTON R R，KITTEL C.On a proposal for determining the thickness of the transition layer between ferromagnetic domains by a neutron polarization experiment［J］.Physical Review，1948，74:1604-1605.

［4］ ROBISCOE R T.A spin flip problem［J］.America J.Physics，1971，39:146-150.

［5］ GRIGORIEV S V，OKOROKOV A I，RUNOV V V.Peculiarities of the construction and application of a broadband adiabatic flipper of cold neutrons［J］.Nucl.Instr.and Meth A，1997，384:451-456.

［6］ SUMBATYAN A A，SLYUSAR V N，OKOROKOV A I，et al..Methods and devices for reversing neutron polarization［J］.Nuclear Experimental Technique，2009，3:30-34.

［7］ LEBEDEV V T，TÖRÖK G.Broadband neutron spin-flippers on magnetized foils［J］.Nuclear Instruments and Methods in Physics Research A，2002，195:449-454.

［8］ REKVELDT M TH，KELLER T，KRAAN W H.New instrumentation using Larmor precession of polarized neutrons［J］.Physica B，2001，297:18-22.

［9］ HOLLEY A T，BROUSSARD L J，DAVIS J L，et al..A high-field adiabatic fast passage ultracold neutron spin flipper for the UCNA experiment［J］.Review Scientific Instruments，2012，83:0735051-07350517.

［10］ TAKEDA T，YAMADA N L，SETO H，et al..Development of spin flippers with steady current for the TOF-NSE spectrometer［J］.Physica B，2003，335:211-214.

［11］ KRAAN W H，GRIGORIEV S V，REKVELDT M TH，et al..Test of adiabatic spin flippers for application at pulsed neutron sources［J］.Nuclear Instruments and Methods in Physics Research A，2003，510:334-345.

［12］ SLYUSAR V N，SOLOVEI V A，SUMBATYAN A A.A triangular-shaped current used in devices for reversing neutron polarization［J］.Instruments and Experimental Techniques，2009，4:50-53.

［13］ KITAGUCHIA M，HINOA M，KAWABATAA Y，et al..Development of neutron resonance spin flipper for high resolution［J］.Physica B，2006，385 386:1128-1130.

［14］ KRAAN W H，REKVELDT M T.Single domain wall in FeNi film on Si as a neutron spin flipper［J］.Nuclear Instruments and Methods in Physics Research A，2008，596:422-429.

［15］ OHOYAMA K，TSUTSUMI K，INO T，et al..Development of a non-adiabatic two-coil spin flipper for a polarized thermal neutron diffractometer with a3He spin filter［J］.Nuclear Instruments and Methods in Physics Research A，2012，680:75-81.

［16］ PYNN R.Broadband spin flippers constructed from thin magnetic films［J］.Physica B，2005，356:178-181.

［17］ WEINFURTER H，BADUREK G，RAUCH H，et al..Inelastic action of a gradient radio-frequency neutron spin flipper［J］.Z.Phys.B，1988，72:195-201.

［18］ FRANK A I，ANDERSON I，BONDAREKO I V，et al..Larmor spin precession and neutron optics［J］.Physics of Atomic Nuclei，2002，65(11):2066-2078.

［19］ 陈良，彭梅，孙良卫，等.使用山嵛酸银标定中子小角散射谱仪关键参数［J］.光学 精密工程，2013，21(7):1755-1762.CHEN L，PENG M，SUN L W，et al..Calibration of key parameters for small angle neutron scattering spectrometer by using silver behenate［J］.Opt.Precision Eng.，2013，21(7):1755-1762.(in Chinese)

［20］ 王晓影，李建，谢超美，等.中子衍射应力谱仪垂直聚焦单色器的优化设计［J］.光学 精密工程，2008，16(10):1880-1885.WANG X Y，LI J，XIE CH M，et al..Optimal simulation of vertical monochromator of neutron diffraction residual stress instrument［J］.Opt.Precision Eng.，2008，16(10):1880-1885.(in Chinese)

［21］ 李新喜，王燕，黄朝强，等.斩盘产生的中子脉冲特性［J］.光学 精密工程，2009，17(9):2112-2119.LI X X，WANG Y，HUANG CH Q，et al..Neutron pulse speciality produced by chop disk［J］.Opt.Precision Eng.，2009，17(9):2112-2119.(in Chinese)

［22］ 李新喜，王燕，黄朝强，等.中子反射谱仪的闸门与会聚导管组合设计［J］.光学 精密工程，2009，17(12):2983-2989.LI X X，WANG Y，HUANG CH Q，et al..Optimized combination of shutters and focus neutron guides for neutron reflectometers peciality produced by chop disk［J］.Opt.Precision Eng.，2009，17(9):2112-2119.(in Chinese)

［23］ 赵凯华，陈熙谋.电磁学［M］.北京:高等教育出版社，2002.ZHAO K H，CHEN X M.Electromagnetics［M］.Beijing:Higher Education Press，2002.(in Chinese)