蓝紫光氮化镓光子晶体面射型激光器

洪国彬，杨钧杰，卢廷昌*

(1.台湾交通大学光电系，中国台湾新竹30050;2.台湾交通大学光电工程研究所，中国台湾新竹30050)

1 引言

数十年来，由于半导体激光器等光电组件研发技术的突飞猛进，使得光电科技产业快速蓬勃发展。进而促使半导体光电科技工艺追求更快速、微小化、低耗能及高功率输出等优点的组件为研究发展目标。近十年来，由于光子晶体(Photonic Crystal)具有优益的光学特性，例如:光能隙(Photonic Bandgap)的形成及光子晶体中的波传调控［1-3］等因素引起产业界及学研机构极大的兴趣，因而在半导体光电组件领域受到许多专家学者的关注。光子晶体可应用于主动光电组件的发展，例如:发光二极管(Light Emitting Diodes)及光子晶体激光器［4-8］。

半导体光子晶体激光器发展至今，常见的型态大致可分成两类:第一类为光子晶体缺陷型激光器(Photonic Crystal Defect Laser)，其共振腔模态设计在光能隙内，因此光无法在缺陷以外的区域存在，使得光只会在此缺陷区域共振而形成光子晶体缺陷型激光器。此种光子晶体激光器可获得较高的品质因子(Quality Factor)、较小的模体积(ModalVvolume)、较大的珀塞尔效应(Purcell effect)及低阈值条件(Threshold Condition)［11-12］。第二类为光子晶体能带边缘型激光器(Photonic Crystal Band-edge Laser)，此种激光器操作于平坦的能带边缘上，由于光波在能带边缘处的群速度趋近于零，在满足特定布拉格绕射条件下而形成驻波。由于具有特定布拉格绕射的特性，某特定波长的光因需满足能量与动量守恒而成为垂直面发射的光，于是此类激光器又称为光子晶体面射型激光器(Photonic Crystal Surface Emitting Laser，PCSEL)［13-15］。其共振腔可以涵盖整个光子晶体结构，所形成的驻波在光子晶体内振荡易于与主动层重合，因此，光子晶体面射型激光器除具有大面积出光外，还有单模操作(Single-mode Operation)、低发散角(Divergence angle)及高功率输出等优点，非常适用于高密度光学储存、微投影机光源、生医感测以及激光器固态照明［3，16］。

在1990年初期，由于氮化镓(GaN)为宽带隙直接带隙半导体，在发光二极管及半导体激光器等领域具有极大的发展潜力，对于提升光电组件性能有相当大的帮助，因而成为研究热点［17-18］。然而早期大多数的面射型激光器均使用GaAs或InP三元或四元化合物为光子晶体的主要材料［19］，主要原因是GaAs及 InP的结晶质量远优于氮化物材料。除此之外，由于GaAs或InP这类化合物所设计的激光器波段为0.98～1.55 μm，使得光子晶体的晶格常数通常大于300 nm，在制作光子晶体时较为容易。相比之下，用于可见光的氮化物系材料所需的光子晶体晶格常数较小，因而不易制作。直到2008年后才有GaN系列光子晶体面射型激光器的文章被发表［4-10］。

另一方面，如何建立一套完善且成熟的数值分析工具用于设计光子晶体面射型激光器是一项艰难且具有挑战性的任务。设计光子晶体结构时，必须先确定使用的晶格常数、晶格种类(如:六角晶格、四角晶格、蜂巢晶格或其它类光子晶体)、光子晶体材料的折射率及其结构图案(边界形状)，进而计算出光子晶体的能带结构及阈值增益(threshold gain)等光子晶体激光器特性。目前常见的计算光能带结构及阈值增益的方法有:平面波展开法(plane wave expansion method)［20］、传输矩阵法(transfer matrix method)、耦合波理论(coupled wave theory)［21］、时域有限差分法(finitedifference time-domain)［22］及多重散射法(multiple scattering method)［23］等。而上述几种方法各自有其优点及极限，例如:平面波展开法受限于无限周期性晶格，对于实际光子晶体并不适用。传输矩阵法仅适合一维的层状结构。耦合波理论可以快速求得阈值条件，但对于边界条件须另外处理;而时域有限差分法则是存在消耗大量计算机资源及计算时间较久的问题;反观多重散射法虽仅适用圆形孔洞之光子晶体，但此法相较于其它方法具有许多优点，如计算时间短，可计算各种晶格之阈值增益及数值结果较为准确等。因此，本文除采用平面波展开法计算能带结构外，主要使用多重散射法探讨光子晶体面射型晶格常数、边界形状及晶格种类等对激光器特性的影响。同时与光子晶体激光器的实验测量结果进行比较。

本文主要研究内容架构大致如下:第2节主要针对多重散射法进行简单的说明及推演;第3节讲述GaN光子晶体面射型激光器的制作流程包含分布式布拉格反射器(Distributed Bragg Reflector，DBR)及光子晶体结构，并介绍激光器特性的光学量测系统;第四节探讨光子晶体晶格常数、边界形状及晶格种类对阈值增益、发散角及偏振度等激光器特性的影响，同时将多重散射法求得的阈值增益与实验测量结果比较;最后总结全文所探讨内容与重要发现。

2 多重散射法

此节主要介绍多重散射法的理论推演［24］。假设二维光子晶体材料性质具有各向同性且由均匀的增益介质所构成，此增益介质称为材料B，而介质中存在一些圆柱形散射体称为材料A。因材料B为增益介质，故介电常数为复数形式，其表示式为:

式中，εb为材料B随光波频率ω变化之介电常数。材料B的波数(wave number)为kB=kbik″b，其中 k″b为增益系数。若视主动层产生的光波进入光子晶体前的光为空间中的光波源，并将此波源所在位置定义为二维坐标系统的原点，如图1所示。

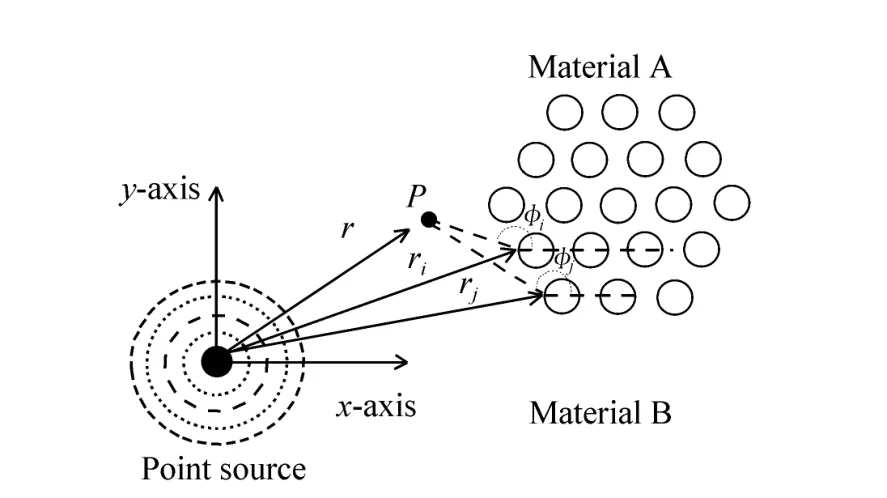
图1 光子晶体结构及点波源示意图Fig.1 Schematic drawing of photonic structure and light source

当空间中的散射体被坐标原点的频率为ω的单频波(monochromatic wave)所照射，这个单频波碰触到散射体后，会因散射体产生散射波向外传播而形成新的波源。而散射体产生的散射波会在各散射体间不断地来回产生多次散射，最后达到稳定状态。因此在空间中，位置r的P点接收到第j个散射体所散射出来的散射电场可表示成:

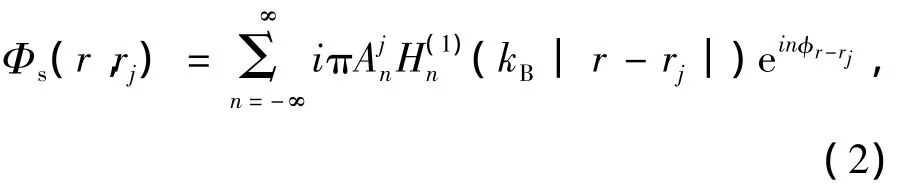
由于入射波在rj处不能有奇异点，于是入射波仅能用第一类贝塞尔函数(Bessel function)迭加展开。因此，第 i个(i=1，2，…，N;i≠j)散射体外的总入射电场可表示成:

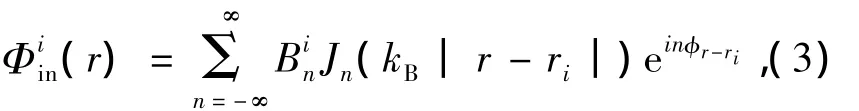
式中，Jn为第一类贝塞尔函数为散射体外入射电场的展开系数。因此，第i个散射体外的总电场为:

同理，第i个散射体内的总电场可表示成:

接着，将散射体内外的总电场可透过电场及其导数在散射体边界处连续的条件，并求解联立方程组则可获得待定系数间的关系式:

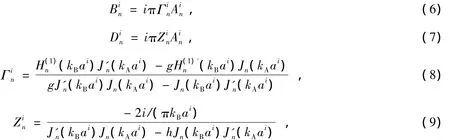
式中，g=f(kB/kA)，f为材料A及B介电常数的比值。h=kA/(gkB)，ai为第i个散射体的半径。由式(6)及式(7)得知，若能求得系数，即可求得散射场内外的电场。于是将入射波源及式(2)透过贝塞尔函数及汉克尔函数的加法定理(addition theorem)［25］，并配合式(3)则可整理出下式:

将式(6)及式(8)代入式(10)，则可整理成:

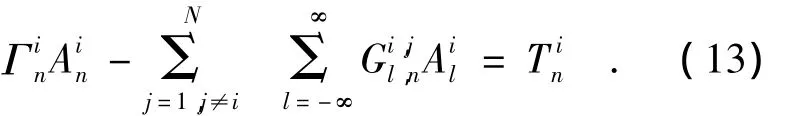
式(13)可整理成 MA=T的形式，因此，透过式(13)求得A，即n阶展开阶数，则散射体内外的电场将可由下列二式求得。

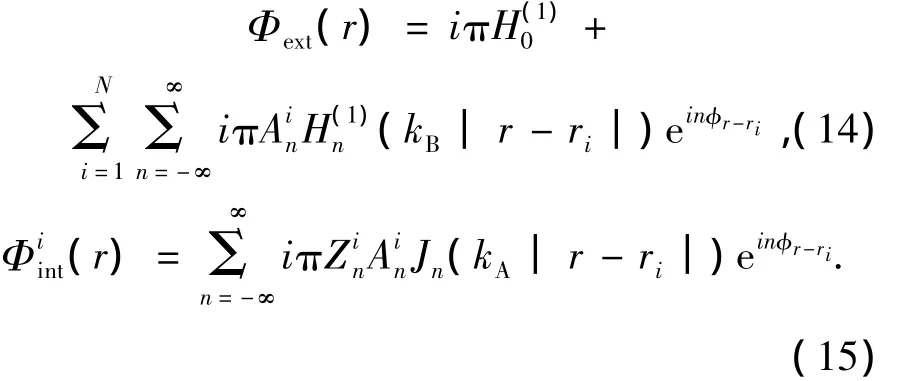
此外，若A/T的值为发散，则达到激光器振荡条件，因此，可由求解复数行列式方程det(M)=0获得一组阈值增益及经由k=ω/c得到归一化频率。

3 光子晶体激光器制作与测量系统

本节主要讲述光子晶体面射型激光器的制作流程及光学测量系统。制作流程可分成两个部分:一为氮化物布拉格反射器的生长;二为光子晶体结构的制作。

3.1 布拉格反射器及微共振腔制作流程

氮化物布拉格反射器及微共振腔的制作使用有机金属化学气相沉积法(metal-organic chemical vapor deposition)将此二结构生长在蓝宝石基板上，其生长过程及实验参数如下:首先，基板加热到1 100℃持续5 min作高温清洁处理，然后将温度降至500℃，并在基板上生长一层30 nm的GaN成核层(nucleation layer)。接着将温度再次提高至1 100℃以生长2 μm厚的GaN缓冲层(buffer layer)。之后同样在1 100℃的高温下生长25(或35)层的1/4λAlN/GaN布拉格反射器，并在DBR上方生长厚度约7个波长的微共振腔。此微共振腔的组成依序为560(或675)nm厚掺杂Si的n型GaN、10 层 In0.2Ga0.8N/GaN 量 子 阱 (quantum well)、24 nm的AlGaN作为电子阻挡层(Electron Blocking Layer)及最后再长上一层 200(或115)nm厚掺杂Mg的p型GaN。在生长布拉格反射器时，在这25层结构中穿插生长AlN/GaN超晶格(Superlattice)，这样有助于释放生长布拉格反射器时所产生的应变。且可进一步改善布拉格反射器界面的质量及提升反射率。除此之外，AlN/GaN布拉格反射器用途为扮演低折射率的角色将光场局限在主动层中。而AlGaN电子阻挡层的作用在于减少电子跑出p型氮化镓层外。

3.2 光子晶体结构制作流程

生长完布拉格反射器及微共振腔后，光子晶体激光器结构最重要的部分就是如何在磊晶晶圆上制作光子晶体。以下就光子晶体面射型激光器结构中，光子晶体纳米结构的制作流程加以说明。

制作光子晶体的步骤为:先在已生长布拉格反射器及微共振腔的晶圆上使用等离子体增强化学气相沉积(PECVD)生长200 nm厚的SiNx，然后在SiN上长一层150(或200)nm的聚甲基丙烯酸甲酯(PMMA)。为了在GaN上制作纳米级的周期性孔洞结构，先以电子束光刻(Electron Beam Lithography)在PMMA的表面定义出光子晶体的晶格常数、晶格种类及边界形状。接着以感应耦合等离子体干式蚀刻(Inductively Coupled Plasma Reactive Ion Etching，ICP-RIE)将光子晶体图案转印至GaN。即在p型GaN干蚀刻出孔洞，其深度约为400 nm。然后依序利用丙酮去除聚甲基丙烯酸甲酯，再用二氧化硅蚀刻液(BOE)将SiN洗掉，便完成光子晶体的制作。其中ICP-RIE蚀刻的深度为400 nm主要是为了将蚀刻出的孔洞穿过多层量子阱以达到光子晶体与主动层的耦合效应。经过上述的制作流程，最后制作出的光子晶体面射型激光器结构如图2所示。图3为六角晶格、四角晶格及蜂巢晶格的扫瞄式电子显微镜(Scanning Electron Microscopy，SEM)影像图。本文后续将针对这3种晶格的光子晶体对激光器特性之影响加以分析与讨论。

图2 光子晶体面射型激光器结构示意图Fig.2 Scheme of PCSEL structure

图3 光子晶体结构电子显微镜影像Fig.3 SEM images of photonic crystal structure

3.3 激光器特性测量系统

当光子晶体激光器结构制作完成后，则可透过光学测量系统，测量光子晶体激光器的激光光谱，角度解析光致发光、发散角等，了解光子晶体激光器基本模态的行为与特性。本文主要介绍的测量系统为角度解析光致发光系统(Angular-Resolved Photoluminescence，ARPL)，其系统设置如图4所示。

图4 角度解析光致发光系统Fig.4 Angular-resolved photoluminescence system

此系统主要由两个光激发源所构成:一为三倍频掺钕钒酸钇(Nd∶YVO4)355 nm脉冲激光器，其脉冲宽度为0.5 ns，重复率为1 kHz;二为325 nm的氦镉(He-Cd)连续波激光器。由改变此两种激光器光束照射至光子晶体的角度达到角度解析的目的，其变化角度为0～60°，最小可变动角度为0.5°。激光器光点大小约为50 μm，可以完整覆盖整个光子晶体。当上述两种激光器光束照射至光子晶体激光器结构，并激发多层量子阱后所产生的光，由放大倍率为15倍及数值孔径(Numerical Aperture，NA)为0.32的物镜收集并过滤掉激光后，经由光纤(纤芯600 μm)将信号送至电荷耦合组件(Charge-Coupled Device)进入光谱计(spectrometer)形成一高分辨率的图像，此光谱计的解析能力为0.07 nm。

4 数值分析与实验测量结果

本文成功生长并制作各种晶格常数、边界形状及晶格种类之GaN光子晶体面射型激光器结构，并通过光学测量系统，测得相关激光器特性，如阈值增益、发散角、偏振度等。利用平面波展开法获得光子晶体的光能带结构及多重散射法求得光子晶体的阈值增益，并与实验结果比较，其结果与实验测得的阈值增益相吻合。由此说明，本文提出的多重散射法作为设计光子晶体激光器结构的数值方法可靠。接下来将针对光子晶体的晶格常数、边界形状及晶格种类之GaN光子晶体面射型激光器特性的影响加以探讨与说明。

4.1 晶格常数的影响

此节为探讨光子晶体的晶格常数对激光器特性的影响。光子晶体制作之参数为六角晶格，如图5所示。其晶格常数(a)为190～300 nm，圆柱孔洞半径(r)与晶格常数之比值(r/a)固定为0.28。光子晶体边界形状为圆形，其直径约为50 μm。

图5 六角晶格于实空间及倒置空间示意图Fig.5 Schematic diagram of the hexagonal lattice in real and reciprocal spaces

图6为室温下测得的激光光强随激发能量密度变化图，样品所对应之晶格常数为290 nm。从图中可清楚地看出激光器的阈值条件激发能量密度为3.5 mJ/cm2，其对应的峰值功率密度为7 MW/cm2。当激发能量超过阈值条件，激光器的光强度则随之迅速增强。

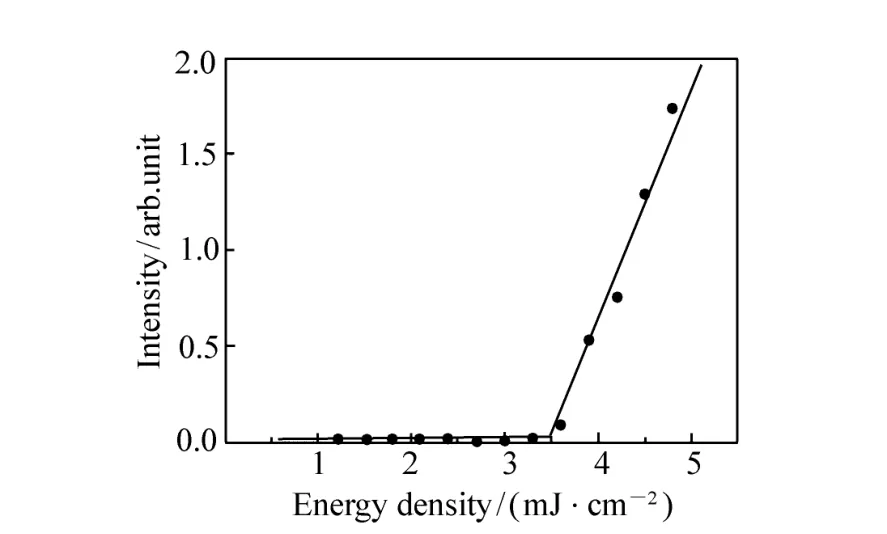
图6 激光器光输出强度Fig.6 Output intensity versus excitation energy density

图7 (a)1.33 倍;(b)1.17 倍;(c)1.00 倍;(d)0.66及(e)0.33倍之阈值能量时的激光器发射光谱Fig.7 Emission spectra of(a)1.33εth，(b)1.17εth，(c)1.00εth，(d)0.66εth，and(e)0.33εth，respectively

图7为室温下不同激发能量的激光器发射光谱，图中(a)～(e)分别表示1.33～0.33倍的阈值能量密度(εth)。从此图中可看出，光子晶体激光光谱只有一个峰值，其峰值波长为424.3 nm，半高宽(FWHM)为0.11 nm。值得注意的是，此单模激光仅出现在光子晶体图案区域内。另一方面，在无光子晶体的区域中，当激发能量密度超过光子晶体激光器阈值能量密度两倍或以上时，始发出多个峰值的光谱，推测其共振腔是由底层布拉格反射器与GaN/空气界面所形成的反射器所构成，说明了光子晶体面射型激光器与传统垂直共振面射型激光器的差异，光子晶体可使激光器结构产生单模操作的特性。

图8为归一化频率(a/λ)随晶格常数变化图，图中圆点为各晶格常数激光的归一化频率，其对应的激光波长为401～425 nm。结果表明，归一化频率随晶格常数变大而增大，且变化呈现不连续的步阶函数状分布。而实线为r/a=0.28的条件下所计算出光子晶体TE模态能带结构图。比较圆点与能带结构可发现，不同晶格常数的激光出现在不同的能带边缘处，如图中虚线所示。这些步阶状分布的圆点恰巧对应至倒置晶格第一布里渊区(Brillouin zone)中的Γ点、K点及M点(如图5(b)所示)。主要是因为这些特殊方向上的晶格点易满足布拉格绕射条件及有较高的状态密度(density of state)所致。

接下来探讨光子晶体激光器的晶格常数为190～260 nm，且r/a由0.18变化至0.3。同图8的分析，光子晶体激光的归一化频率可分成3个区段，分别为0.48、0.56及0.59，其对应的晶格常数为190、210及230 nm。本文将对应至Γ点、K点及M点上的模态定义为Γ1模态、K2模态及M3模态。并透过ARPL系统沿着Γ-K及Γ-M方向(如图5(b)所示)测量光子晶体的绕射图案，进而了解光子晶体激光器的垂直面发射特性。

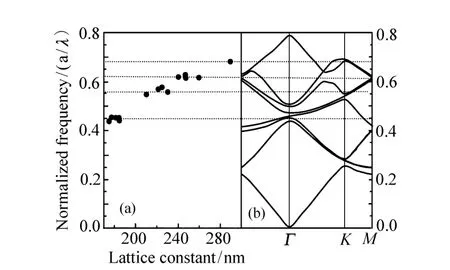
图8 归一化频率随晶格常数变化图Fig.8 Normalized frequency a versus the lattice constant

图9 Γ1模态之角度解析光致发光光谱Fig.9 Measured ARPL diagram near the Γ1mode

图9为透过ARPL系统测量的Γ1模态的绕射图案，图中虚线为Γ点附近的能带结构仿真结果。由于YVO4脉冲激光器的激发能量较高，可以清楚看出光子晶体激光器垂直面射的角度接近激光器结构表面的法线方向。另外，YVO4脉冲激光器因激发能量太强，激发光谱中无法明显观察到绕射线。然而，若使用He-Cd连续波激光器激发，其光谱中便可清楚地看到绕射图案。图中微向上弯曲曲线的产生，是由于激光器垂直方向上的p-i-n GaN层及氮化物布拉格反射器产生的干涉而衍生出法布里-珀罗效应(Fabry-Perot effect)所造成。除此之外，在图中可观察到一些不同斜率的绕射线，这些线代表着不同的绕散模态，其中一些绕射线与仿真结果(如虚线)匹配。而那些具有相同斜率的绕射线指的是光子晶体平面方向的波导模态。另一方面，从模拟结果得知，在Γ点附近应有4个相似的能带边缘模态，但是ARPL只观察到主要的激光峰值出现在第二低的能带边缘，而次要的峰值出现在最低的能带边缘。主要是此两能带边缘模态的光场相较于另两个较高的能带边缘模态与主动层的耦合较强，因而在光学测量上无法同时观察到这四个态模同时产生。同样地，在K点及M点的角度解析光致发光也有类似图9的情况。

图10为Γ1、K2及M3模态的发射角度和发散角度之比较图，由此图可清楚地了解不同模态发射角度与发散角度的差异。这3种模态的激光发射角度分别为 0°、29°及 59.5°，其所对应的发散角分别为1.2°、2.5°及2.2°。从发射角度的测量中可发现，测量结果与布拉格绕射机制理论值吻合。然而，K2及M3模态的发射角度与理论值(30°及61.87°)有着微小的差异，特别是M3模态。主要是因为ARPL系统部分组件在对齐样品上有一些困难，因而测量结果可能存在1°～2°的偏差。另外，图中K2及M3模态的光谱存在一些次要峰值，主要是因为K2及M3模态需较高的阈值增益才能激发出这些模态，因而较高的激发能量使得其它在氮化镓层及基板传播的波导模态出现在光谱上。

图10 Γ1、K2及M3模态之发射角度和发散角度Fig.10 Emission and divergence angles of Γ1，K2，and M3modes

以上结果说明光子晶体的晶格常数对激光器模态(Γ1、K2及M3)的产生有着极大的影响。这表示可由改变晶格常数的方式达到调变激光器模态的行为。另外值得注意的是，不论是何种模态，本文所制作的光子晶体激光器验证了光子晶体激光器具有单模操作及低发散角的优点。

4.2 边界形状的影响

此节将介绍光子晶体边界形状对光子晶体激光器的特性影响。本节所探讨的激光器结构的光子晶体由六角晶格组成，其晶格常数为190 nm，而孔洞半径与晶格常数之比值(r/a)为0.3。制作光子晶体激光器结构时，光子晶体的边界形状可分成圆形及六角形两种，其各自的电子显微镜影像如图11所示。

图11 光子晶体电子显微镜影像Fig.11 SEM images of photonic crystal

图12 光能带结构及归一化频率Fig.12 Photonic band diagram normalized frequencies

图12为平面波展开法求得Γ点附近之能带结构与多重散射法求得的归一化频率。由能带结构图可发现，在Γ点附近共有4个主要的共振模态，如图12(a)中标示的A至D，其中模态B及D为双重简并模态。而使用多重散射法计算出之归一化频率亦有4个共振模态，如图12(b)中4条曲线。从图12(b)可看出，当计算时的壳层数(如图5(a)之虚线圈数)大于20时，此4个模态的归一化频率即收敛至定值，且此4个模态分别对应至图12(a)中的模态A、B、C及D。特别值得一提的，多重散射法求得的模态B与C的归一化频率随着壳层数增加时有红移及蓝移的现象。其原因为模态B靠近Γ点附近的能带曲线为开口向上，而模态C则是开口向下。同理，模态A与D附近的能带变化为开口向下及向上，当壳层数增加时具有蓝移与红移的行为。由图12了解平面波展开法与多重散射法之间的关系与差异后，接下来将使用多重散射法计算光子晶体的阈值增益。

图13为阈值增益随填充因子(filling factor)变化关系图。计算阈值增益时，采用有效介电常数法［26-27］求得空气圆柱及GaN的有效介电常数，并代入多重散理论模型进而求得模态A至D的归一化频率。其有效介电常数的计算方式为Δε =εb－εa，f为填充因子，Ω =0.865为限制因子(confinement factor)及neff=2.482为有效折射率。经由上述的计算，当 r/a=0.3时，可求得εb=7.484及 εa=3.065，其中 εb为 GaN 光子晶体之介电常数的实部，如式(1)的实数部分，而εa则是空气圆柱的等效介电常数。

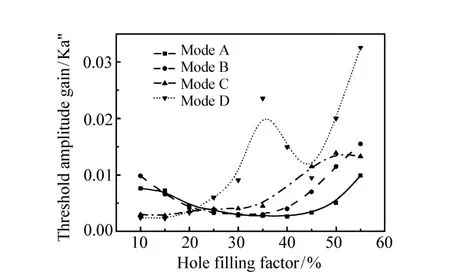
图13 阈值增益随填充因子变化曲线Fig.13 Threshold gain as a function of the filling factor

从此图可发现，4个模态ABCD的最小阈值增益出现在填充因子为35%、30%、10%及15%时。此结果说明制作光子晶体时，填充因子可作为调控激光器操作模态的控因，即选择特定的填充因子后便决定了激光的操作模态。另外，从角度解析光致发光光谱发现，光子晶体激光器操作于Γ点附近的模态B，其结果与多重散射法的分析结果相匹配。其理由为本节所探讨的光子晶体的填充因子约为32.6%，而从图13得知，当填充因子接近30%时，模态A与B有最小的阈值增益。并承上节ARPL的测量结果，Γ点附近仅有Γ1模态出现。且由于模态A的频率与主动层增益峰值之位置有较大的偏移量，于是模态A与主动层的耦合较差，因而ARPL的测量无法观察到模态A的存在。

图14 激光输出强度Fig.14 Output intensity versus excitation energy

由上述结果了解激光将操作于何种模态后，然后将比较不同边界形状的光子晶体激光器特性的差异。由激光器发射光谱的测量得知圆形边界与六角形边界的激光器波长分别为403 nm与406 nm，其光谱的半高宽为0.25 nm与0.28 nm。此外，图14为圆形边界与六角形边界的光子晶体激光器的激光输出光强度随激发能量密度的变化曲线，其激光强度在室温下由光点大小为50 μm的355 nm YVO4脉冲激光器所激发。其结果显示，圆形边界与六角形边界的阈值激发能量密度为2.8 mJ/cm2与3.1 mJ/cm2。同时，在相同参数下，多重散射法求得的阈值增益分别为2.784×10－3及 3.798 ×10－3。实验测量及理论计算的结果呈现了圆形边界之光子晶体有较小的阈值条件。其原因可能为圆形边界的光子晶体，因图形的对称性提供光在光子晶体内有较多的对称性反射，进而容易达到激光器阈值。

上述结果说明了多重散射法的模拟与实验结果相吻合，非常适用于设计光子晶体激光器结构。同时，光子晶体的边界形状对激光器波长及其半高宽的影响似乎无显著的变化。相较于六角边界，采用圆形边界其激光器阈值能量约可降低0.3 mJ/cm2。

4.3 晶格种类的影响

本节为比较不同晶格种类的差异，针对六角晶格、四角晶格、蜂巢晶格的晶格常数加以设计，使得这3种晶格具有相同的激光波长。因此，这3种晶格在具有相同的倒置晶格向量的条件下，其晶格常数的比例为 3.464∶3∶2［9］，而实际制作之光子晶体的晶格常数分别为 176、150及100 nm，其边界形状为圆形，直径约为40 μm。

图15 激光器光输出强度Fig.15 Emission intensity as a function of the pumping energy

图15为在室温下不同晶格的激光输出强度随激发能量密度的变化曲线。由此图可知六角晶格、四角晶格、蜂巢晶格的激光阈值条件分别为2.3、3.8及1.6 mJ/cm2。在此3种晶格中，蜂巢晶格的阈值能量密度最小。主要原因为靠近能带边缘处的光能带较其它晶格平坦，使得蜂巢晶格有较高的光子状态密度。因此，蜂巢晶格有较多的光子与主动层交互作用而使阈值条件降低［28-30］。

当激发能量高于阈值条件，则可测得激光光谱，如图16所示。在室温下测得六角晶格、四角晶格及蜂巢晶格的激光波长为别为391.4、391.7及393.8 nm。此数据说明了，这3种晶格之激光器结构操作在相似的光学增益范围。依据各晶格之晶格常数所计算出归一化频率分别为0.447、0.383及0.254。这些光子晶体激光器操作于Γ点能带边缘［24］，与本文设计相当接近。

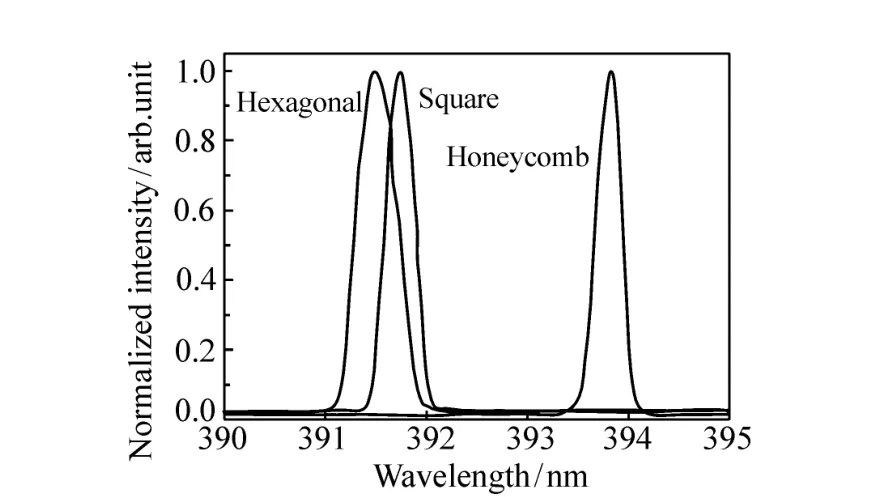
图16 激光器光发射光谱Fig.16 Emission spectra for different lattice types

图17为3种晶格的阈值能量密度实验测量值及多重散射法求得的阈值增益。由阈值能量密度实验值可以看出，蜂巢晶格的阈值能量较低，且六角晶格及四角晶格的阈值能量分布范围较蜂巢晶格大。相较于实验值，使用多重散射法时，空气圆柱与GaN的有效拆射率分别为1.87及2.65，在此参数下计算出Γ1模态阈值增益。结果显示蜂巢晶格的阈值增益在三者之中最小，而四角晶格的阈值增益最大，与实验结果有相同的趋势。

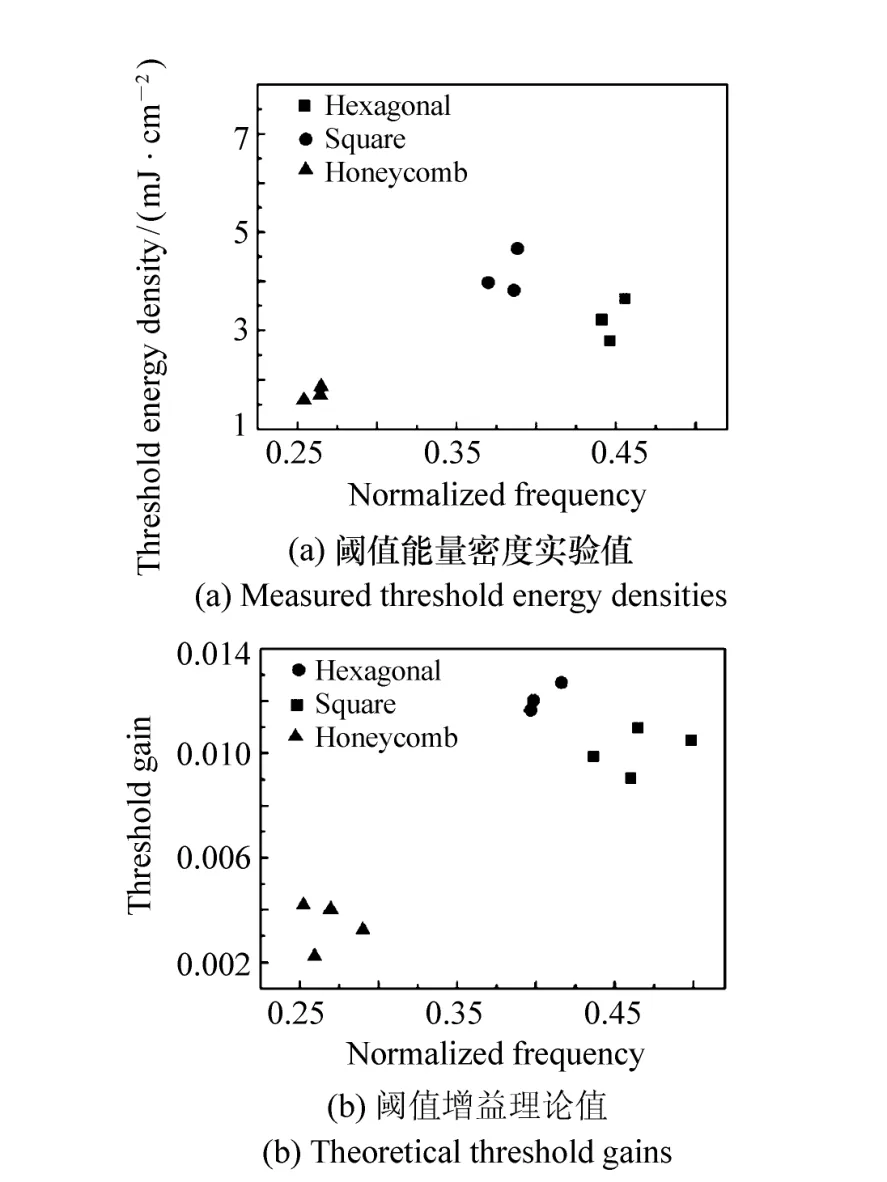
图17 阈值能量密度实验值及阈值增益理论值Fig.17 Measured threshold energy densities and theoretical threshold gains

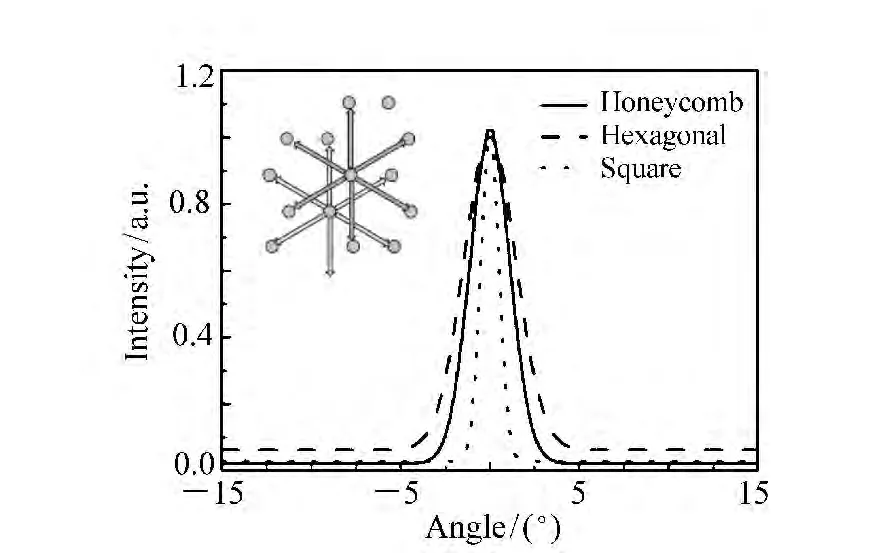
图18 Γ1模态之发散角Fig.18 Divergence angles of Γ1mode

图18为六角晶格、四角晶格及蜂巢晶格的发散角测量结果，其实验测量的角度分辨率为0.5°。测量结果显示，这3种晶格的发散角分别为1.7°、2.2°及 1.3°。这些数据说明，此 3 种晶格的激光垂直于激光器结构的表面。依据多方向分布反馈(Multidirectional Distributed Feedback)原理，若光子晶体面射型激光器垂直出光，即表示此激光器操作于Γ点能带边缘。此结果验证了本文的设计，同时，从测量结果可以发现，蜂巢晶格的发散角最小。其原因可归究于倒置空间中k向量的耦合。图18的插图为蜂巢晶格的倒置晶格，其箭头为倒置空间k向量。由于晶格结构的不同，蜂巢晶格比六角晶格及四角晶格有较多的倒置空间k向量，使其易于满足特定布拉格绕射条件而形成垂直面射出光的情况，因而蜂巢晶格有较小的发散角。

图19为六角晶格的极化曲线测量结果，图中黑点为实验值。四角晶格及蜂巢晶格也有相似的结果。本文为了解激光偏振程度(Degree of Polarization，DOP)，依据极化曲线量的测量结果可求得六角晶格、四角晶格及蜂巢晶格的偏振度分别为73%、70%及86%。

图19 六角晶格之极化曲线Fig.19 Measured polarization curves of hexagonal lattice

一般而言，对于GaN光子晶体面射型激光器，因倒置空间k向量提供的对称反馈机制使其偏振度较低。然而，实验结果呈现3种晶格的偏振度高达70%以上，其中以蜂巢晶格为最高。原因可能为激光器结构本身存在一些缺陷及光子晶体的周期性不够完美，造成本应提供对称反馈的k向量，无法在对称的晶格点上产生相同的绕射，而是在其它方向上产生绕射反馈，因而使得激光的偏振度相对提高。

5 结论

本文成功制备了GaN光子晶体面射型激光器结构，并由角度解析光致发光系统分析光子晶体面射型激光器的光学特性。同时，使用平面波展开法及多重散射法计算光子晶体的能带结构与阈值增益。实验结果显示，由改变光子晶体的晶格常数即可达到调变激光器发光模态的目的。此外，光子晶体的边界形状对激光波长及半高宽的影响并无显著的改变。相较于六角边界，采用圆形边界约可降低约0.3 mJ/cm2的阈值能量。另一方面，比较晶格种类对激光器特性的影响中发现，蜂巢晶格具有较小的激发能量密度(1.6 mJ/cm2)及发散角(1.3°)，但激光的偏振度高达86%。反观四角晶格的激发能量密度(3.8 mJ/cm2)及发散角(2.2°)为三者之中最大，且偏振度为70%。而六角晶格则介于两者之间，偏振度与四角晶格相似，但激发能量密度只有四角晶格的60%。在理论计算方面，多重散射法的模拟与实验结果相吻合，非常适用于设计光子晶体激光器结构。综上所述，光子晶体面射型激光器将有益于高功率低阈值激光器的发展。同时本文的激光器制作流程及多重散射法在未来可应用于GaAs、InP及ZnO等半导体光子晶体激光器，作为快速设计与制作的依据。

［1］ YABLONOVITCH E.Inhibited spontaneous emission in solid-state physics and electronics［J］.Phys.Rev.Lett.，1978，58(20):2059-2062.

［2］ JOHN S.Strong localization of photons in certain disordered dielectric superlattices［J］.Phys.Rev.Lett.，1987，58(23):2486-2489.

［3］ MEIER M，MEKIS A，DODABALAPUR A，et al..Laser action from two-dimensional distributed feedback in photonic crystals［J］.Appl.Phys.Lett.，1999，74(1):7-9.

［4］ SIRIGU L，TERAZZI R，AMANTI I，et al..Terahertz quantum cascade lasers based on two-dimensional photonic crystal resonators［J］.Opt.Express，2008，16(8):5206-5217.

［5］ MATSUBARA H，YOSHIMOTO S，SAITO H，et al..GaN photonic-crystal surface-emitting laser at blue-violet wavelengths［J］.Science，2008，319(5682):445-447.

［6］ LU T C，CHEN S W，LIN L F，et al..GaN-based two-dimensional surface-emitting photonic crystal lasers with AlN/GaN distributed Bragg reflector［J］.Appl.Phys.Lett.，2008，92(1):011129-011129-3.

［7］ KAWASHIMA S，KAWASHIMA T，NAGATOMO Y，et al..GaN-based surface-emitting laser with two-dimensional photonic crystal acting as distributed-feedback grating and optical cladding［J］.Appl.Phys.Lett.，2010，97(25):251112-251112-3.

［8］ LAI C F，KUO H C，YU P，et al..Highly-directional emission patterns based on near single guided mode extraction from GaN-based ultrathin microcavity light-emitting diodes with photonic crystals［J］.Appl.Phys.Lett.，2010，97(1):013108-013108-3.

［9］ IWAHASHI S，KUROSAKA Y，SAKAI K，et al..Higher-order vector beams produced by photonic-crystal lasers［J］.Opt.Express，2011，19(13):11963-11968.

［10］ WU T T，WENG P S，HOU Y J，et al..GaN-based photonic crystal surface emitting lasers with central defects［J］.Appl.Phys Lett.，2011，99(22):221105-221105-3.

［11］ PAINTER O，LEE R K，SCHERER A，et al..Two-dimensional photonic band-gap defect mode Laser［J］.Science，1999 284(5421):1819-1821.

［12］ PARK H G，KIM S H，KWON S H，et al..Electrically driven single-cell photonic crystal laser［J］.Science，2004，305(5689):1444-1447.

［13］ WENG P H，WU T T，LU T C，et al..Threshold gain analysis in GaN-based photonic crystal surface emitting lasers［J］.Opt.Lett.，2011，36(10):1908-1910.

［14］ CHEN S W，LU T C，KAO T T.Study of GaN-based photonic crystal surface emitting lasers with AlN/GaN distributed Bragg reflectors［J］.IEEE J.Select.Topics Quantum Electron.，2009，15(N3):885-891.

［15］ LU T C，CHEN S W，KAO T T，et al..Characteristics of GaN-based photonic crystal surface-emitting lasers［J］.Appl.Phys.Lett.，2008，93(11):111111-111111-3.

［16］ NAKAMURA S，SENOH M，IWASA N，et al..High-brightness InGaN blue，green and yellow light-emitting diodes with quantum well structures［J］.Jpn.J.Appl.Phys.，1995，34:L797-L799.

［17］ NAKAMURA S，SENOH M，NAGAHAMA S，et al..Room-temperature continuous-wave operation of InGaN multi-quantum-well-structure laser diodes with a long lifetime［J］.Appl.Phys Lett.，1997，70(7):868-870.

［18］ OHNISHI D，OKANO T，IMADA M，et al..Room temperature continuous wave operation of a surface-emitting two-dimensional photonic crystal diode laser［J］.Opt.Express，2004，12(8):1562-1568.

［19］ HUNG C T，SYU Y C，WU T T，et al..Design of low threshold photonic crystal surface emitting lasers［J］.IEEE Photon.Techn.Lett.，2012，24(N10):866-868.

［20］ SAKODA K，OHTAKA K，UETA T.Low-threshold laser oscillation due to group-velocity anomaly peculiar to two-and three-dimensional photonic crystals［J］.Opt.Express，1999，4(12):481-489.

［21］ LEE Y H，RYU H Y，NOTOMI M.Finite-difference time-domain investigation of band-edge resonant modes in finite-size two-dimensional photonic crystal slab［J］.Phys.Rev.B，2003，68(4):045209-045209-8.

［22］ SAKAI K，YUE J，NODA S.Coupled-wave model for triangular-lattice photonic crystal with transverse electric polarization［J］.Opt.Express，2008，16(9):6033-6040.

［23］ NOJIMA S.Theoretical analysis of feedback mechanisms of two-dimensional finite-sized photonic-crystal lasers［J］.J.Appl.Phys.，2005，98(4):043102-043102-9.

［24］ WENG P H，WU T T，LU T C.Study of band-edge modes in gan-based photonic crystal surface emitting lasers by the multiple scattering method［J］.IEEE J.Select.Topics Quantum Electron.，2012，18(6):1629-1635.

［25］ CHEN Y Y，YE Z.Propagation inhibition and wave localization in a two-dimensional random liquid medium［J］.Phys.Rev.E.，2002，65(5):056612-056612-5.

［26］ IMADA M，CHUTINAN A，NODA S，et al..Multidirectionally distributed feedback photonic crystal lasers［J］.Phys.Rev.B，2002，65(19):195306-195306-8.

［27］ CHEN S W，LU TC，HOU Y J，et al..Lasing characteristics at different band edges in GaN photonic crystal surface emitting lasers［J］.Appl.Phys.Lett.，2010，96(7):071108-071108-3.

［28］ KIM S，PARK Y，HWANGK，et al..High-power and large-alignment-tolerance fiber coupling of honeycomb-lattice photonic crystal Γ-point band-edge laser［J］.J.Opt.Soc.Am.B，2009，26(7):1330-1333.

［29］ LEE P T，LU T W，SIO K U.Multi-functional light emitter based on band-edge modes near Γ-point in honeycomb photonic crystal［J］.J.Lightwave Technol.，2011，29(12):1797-1801.

［30］ KIM D U，KIM S，LEE J，et al..Free-standing GaN-based photonic crystal band-edge laser［J］.IEEE Photon.Technol.Lett.，2011，23(20):1454-1456.