Simulation on the law of wave-front shaping with stochastic parallel gradient descent algorithm for adaptive optics
2014-11-26王卫兵,王挺峰,郭劲
1 Introduction
How to shape distortion wave-front produced by atmospheric turbulence is a study focus in optical communications and optical imaging.Recently,many institutions have been doing many researches on distortion wave-front shaping by controlling deformable mirrorwith stochastic parallelgradientdescent(SPGD)algorithm.This adaptive optics system without wave-front sensor can cut down the cost of system and solve the problem that wave-front can't be detected because of light spot scintillation[1].
In 1997,M.A.Vorontsov et.al successfully used SPGD algorithm in adaptive phase-distortion correction[2],and then used SPGD algorithm in laser focusing,laser communications,APPLE system[3]and astronomy imaging.In 2000,M.A.Vorontsov et.al investigated convergence rate of SPGD algorithm by controlling different elements liquidcrystal phase modulator[4].In 2009,Yang Huizhen et al.made many simulations for shaping distortion wave-front described by 3~104 order Zernike aberrations by controlling 61-unit deformable mirror with SPGD algorithm from convergence rate and image quality of SPGD algorithm,and achieved good shaping effects[5].It can be found from many relative papers[1-8]involved with SPGD algorithm that no one has investigated in detail and systematically the change laws of convergence rate,shaping capability and shaping effect of SPGD algorithm.In this paper we focus on the above problems.
We use 6 frames of different distortion degree of initial wave-front described by 3~119(117)order Zernike aberrations with Roddier method[9]as shaping objects and 6 kinds of different unit deformable mirror as shaping device,and construct wave-front shaping system with SPGD algorithm for adaptive optics by selecting appropriate algorithm parameters,and make detailed simulations for the law of adaptive optics for wave-front shaping with SPGD algorithm in atmospheric turbulence.
2 Principle of wave-front shaping with SPGD algorithm based on Zernike mode for adaptive optics in atmospheric turbulence
2.1 Wave-front shaping theory based on Zernike mode in atmospheric turbulence
The degree of atmospheric turbulence can be measured by atmospheric coherence length r0,and produced distortion wave-front can be analyzed by Zernike mode method.Results achieved by Noll show that Zernike mode is not independent in statistic.And Roddier solved this problem with Karhunen-Loeve function by metric computations,and all wave-front phase can be fitted by Zernike polynomials.Distortion wave-front described by 3~M+3(total:M)order Zernike aberrations(not including Zernike tilt aberrations)with Roddier method[9]is expressed as
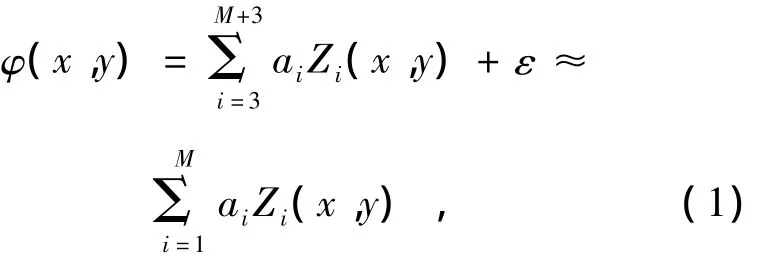
where ε is fit residua neglected,Zi(x,y)is i-th Zernike polynomial and aiis the corresponding coefficient.Expression(1)shows clearly that M,aiand Zi(x,y)all influence distortion degree of wavefront,and number of aiand Zi(x,y)is M.When M is fixed,Zi(x,y)is also fixed.So distortion degree of wave-front mainly depends on M and ai.By this way can we obtain different wave-front with different M and ai.Surface function(or phase compensation)of N-unit deformable mirror[5,7]is expressed as
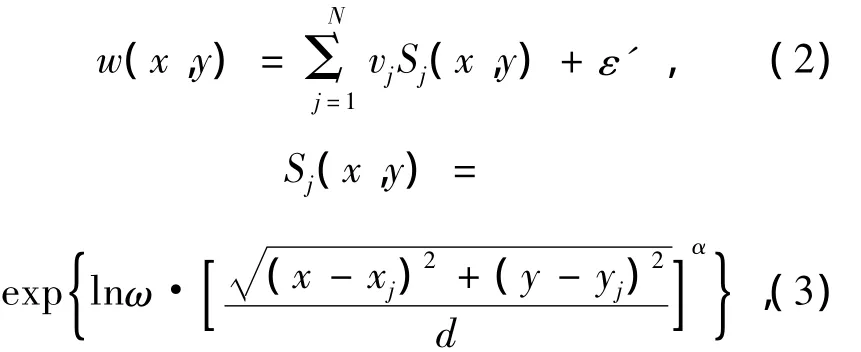
where ε'is fit residua neglected,ω is the coupling value between actuators,d is the distance between actuators and α is the Gaussian index.j is j-th actuator of deformable mirror,Sj(x,y)is response function of the j-th actuator,(xj,yj)is location of the jth actuator and vjis control voltage of the j-th actuator.
If using the same Zernike polynomials Zi(x,y)to fit Sj(x,y),Sj(x,y)can be expressed as
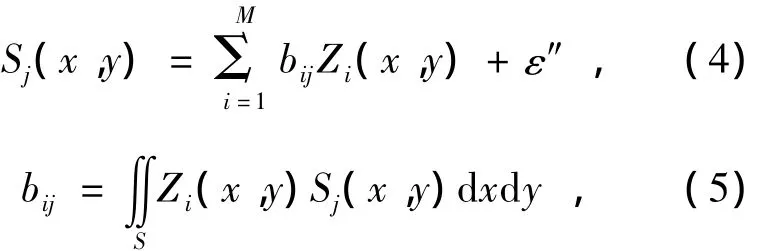
where ε″is fit residua neglected,bijis the constant coefficient coupled by Sj(x,y)and Zj(x,y).Because Sj(x,y)and Zj(x,y)are selected in advance,all bijcan compose a constant coupled metric BM×N.
Then residual wave-front φ(x,y)in the shaping course can be expressed as:
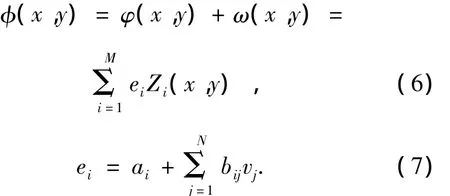
Strehl ratio(SR)is a universal performance evaluation index,and express far field intensity ratio between distortion wave-front and ideal wave-front at light axis.By the orthogonality of Zernike polynomials in unit circle and the principle of physics optics,performance index of residual wave-front J can be simplified as

Besides,expression(8)describes the principle of adaptive optics wave-front shaping and has some theoretical meanings.From above analysis we know that distortion wave-front depends on A and M;deformable mirror depends on N at some conditions;constant coupled metric B depends on M and N.So we can further achieve the relationship between performance index and shaping object,and shaping device can be expressed as

where J0is performance index of initial distortion wave-front and reflect distortion degree of initial wave-front at some extent.Expression(9)is more obvious to describe the essence of adaptive optics for wave-front shaping.We next investigate the law of wave-front shaping with SPGD algorithm by selecting different J0(by changing A),M and N.
2.2 SPGD algorithm
SPGD algorithm can shape distortion wave-front by controlling actuator voltage of deformable mirror,and the procedure of bilateral SPGD algorithm is as follows[1]:
(1)Produce initial actuator voltage V(0)=and obtain initial performance index
(2)The n-th iterative voltage isand the corresponding performance index is
(3)Produce the n-th small random perturbation voltageand the amplitude is
(4)Then obtain
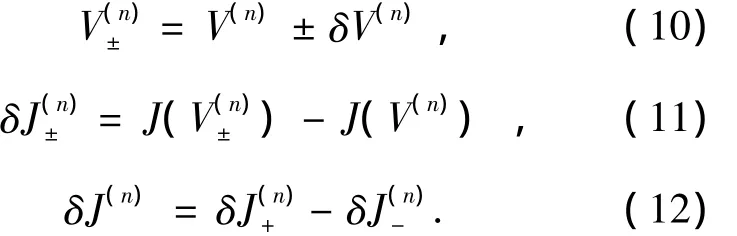
(5)Compute(n+1)-th iterative voltage is
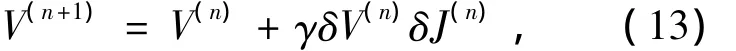
where γ is gain coefficient;
(6)Make program circulate from(2)to(5)until it satisfies stop condition of program,and iterations n or performance index J can be selected as the stop program.
3 Simulation model
Work principle of wave-front shaping system with SPGD algorithm for adaptive optics[7]shown in Fig.1 is that performance index J and its variety ΔJ can be computed by performance index analyzer from data collected by CCD,and then the control voltage of deformable mirror V=v1,v2,……vNis obtained from ΔJ by SPGD algorithm.Circulate this work course according to above procedure until satisfy the stop condition of SPGD algorithm.The essence of system is that the best control voltage of deformable mirror Vbest={v1,v2……vN}can be gradually found by SPGD algorithm,which makes performance index J gradually approach to 1 and residual wave-front φ(x,y)gradually become ideal planar wave-front by gradually changing surface function of deformable mirror w(x,y).
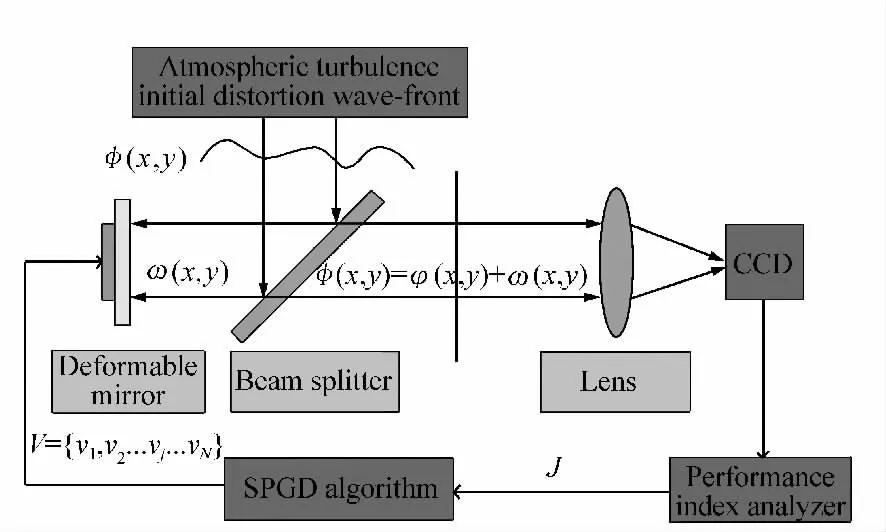
Fig.1 Wave-front shaping system for with SPGD algorithm for adaptive optics
127,91,61,37,19,7[4]-unit deformable mirror were selected as shaping devices and ω=0.08,α =2 shown in Fig.2.Atmospheric coherence length ro=13 cm[10]and caliber of receiving device D=1.2 m were selected,and then 6 frames of distortion wave-front were produced randomly including 3~119(117)order Zernike aberrations with Roddier method as shaping objects shown in Fig.3.And γ =30,δ=0.1 and V(0)={0,0…0…0}were selected in bilateral SPGD algorithm.Then we use Matlab7.8.0 to make simulation experiments respectively for the change law of convergence rate,shaping capability,shaping effect by selecting different combinations among J0,M and N in computer of Pentium(R)Dual-Core CPU E5300@2.60 GHz 2.62 GHz and 32-bit operating system,where J0is shown in Fig.3,M=117,88,63,42,25,12,and N=127,91,61,37,19,7.

Fig.2 N-unit deformable mirror(N:127,91,61,37,19,7)

Fig.3 6 frames of initial distortion wave-front distribution including 3 ~119(117)order Zernike aberrations(a:J10=0.0190,b:J20=0.0888,c:J30=0.1601,d:J40=0.2626,e:J50=0.3424,f:J60=0.5265)
4 Simulation results
4.1 Qualitative results of convergence rate of SPGD algorithm
We select iterations n=1 500 as the stop condition of SPGD algorithm,and achieve 216 sets of convergence curve about the relationship between J and n for different J0,M and N shown in Fig.4.A large scale of simulation figures are the same with Fig.4 in some range of J0,which mean that convergence course of SPGD algorithm is stable,so selecting randomly a set of results to analyze.We use curve slop dJ/dn to measure convergence rate of SPGD algorithm.Although the local results change,the whole results show that convergence rate increases as Zernike orders M decreases for given J0and N,increases as actuator number of deformable mirror N decreases for given J0and M,and increases as distortion degree of initial wave-front decreases or J0increases for given M and N,where the two latter is more obvious than the former.From expression(8)we can find that the element number MN of coupled constant metric B influences convergence rate,and the fewer MN is,the bigger convergence rate is.So the results are consistent with theoretic analysis.If we use needed iterations up to the same performance index described as nJor obtained performance index by the same iterations described as Jnto measure convergence rate,achieved conclusions are the same with above conclusions.Besides,it's difficult to obtain quantitative results about convergence rate because it have relations with parameters such as irritations n,voltage amplitude σ,gain coefficient γ and so on[7].
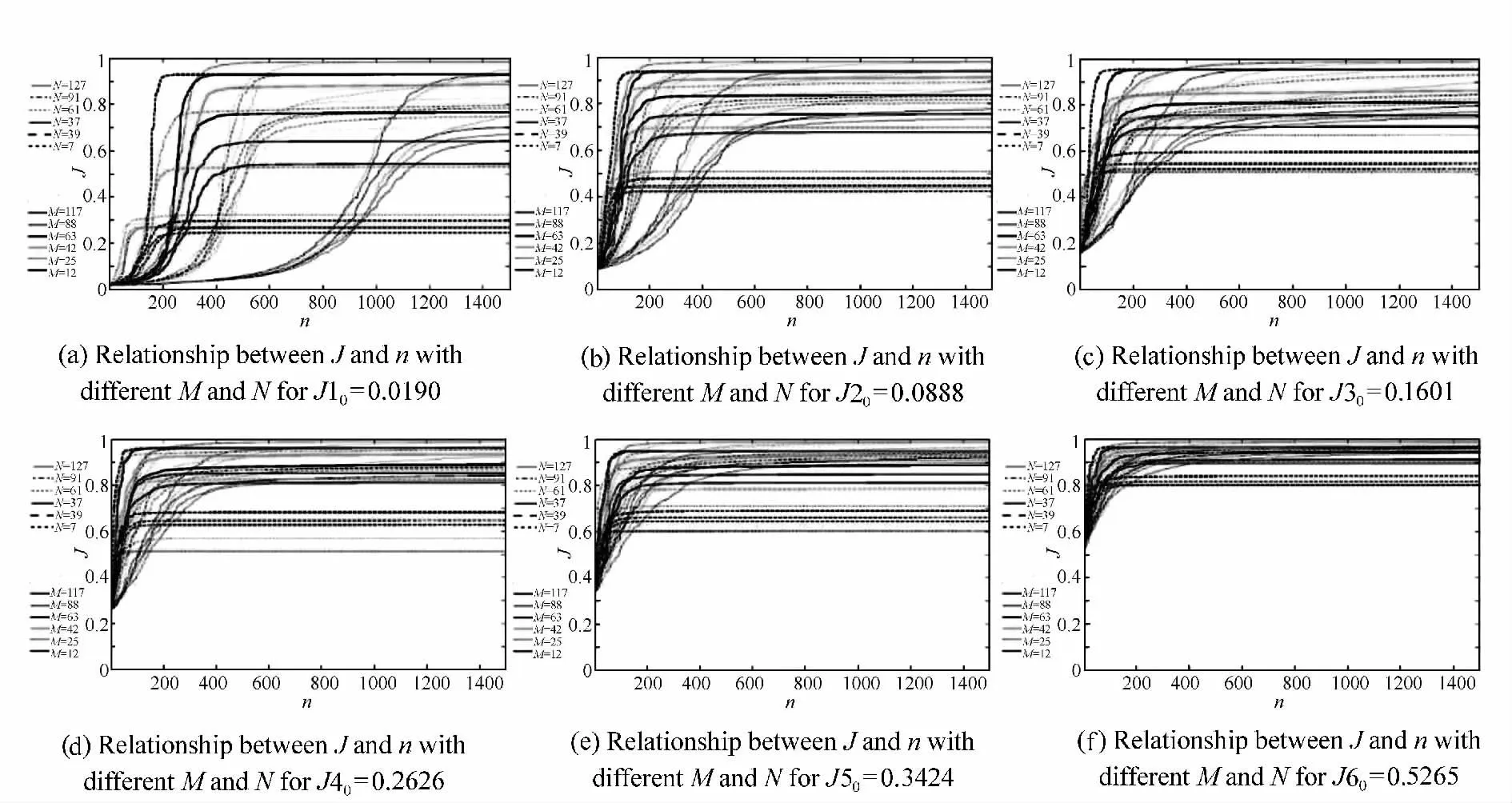
Fig.4 216 sets of convergence curves about the relationship between J and n for different J0,M and N(a.J10=0.0190,b.J20=0.0888,c.J30=0.1601,d.J40=0.2626,e.J50=0.3424,f.J60=0.5265)
4.2 Qualitative and quantitative results of shaping capability of SPGD algorithm
We can find that every curve will converge to performance index limitation Jlim.Here we select irritations n=5 000 as the stop condition of SPGD algorithm,make J5000=Jlimand use Jlimto measure shaping capability of SPGD algorithm.Shaping capability Jlimfor different J0,M and N are shown in Tab.1,and corresponding 3 dimension figure are shown in Fig.5(a).Although the local results change,the whole results show that shaping capability increases as Zernike orders M decreases when M≥25 and decreases as M decreases when M≤25 for given J0and N,increases as actuator number of deformable mirror N decreases when N≥91 and decreases as N decreases when N≤91 for given J0and M,and increases as distortion degree of initial wavefront decreases or J0increases for given M and N,where the two latter is more obvious than the former.Besides,the results also show that shaping capability is the best when M=42 and N=91.We can achieve quantitative expression(14)of shaping capability about different J0,M and N with the least square method,and corresponding fitting surfaces for 6 frames of different initial distortion wave-front are shown in figure Fig.5(b).Comparisons between Fig.5(a)and Fig.5(b)indicate that expression(14)can reflect the change law of shaping capability.We can obtain more accurate quantitative expression if we make segment solution or use more data to fit.
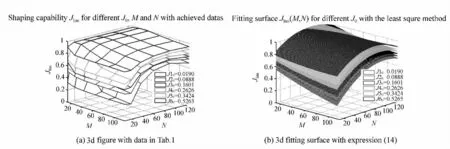
Fig.5 Shaping capability Jlimfor different J0,M and N

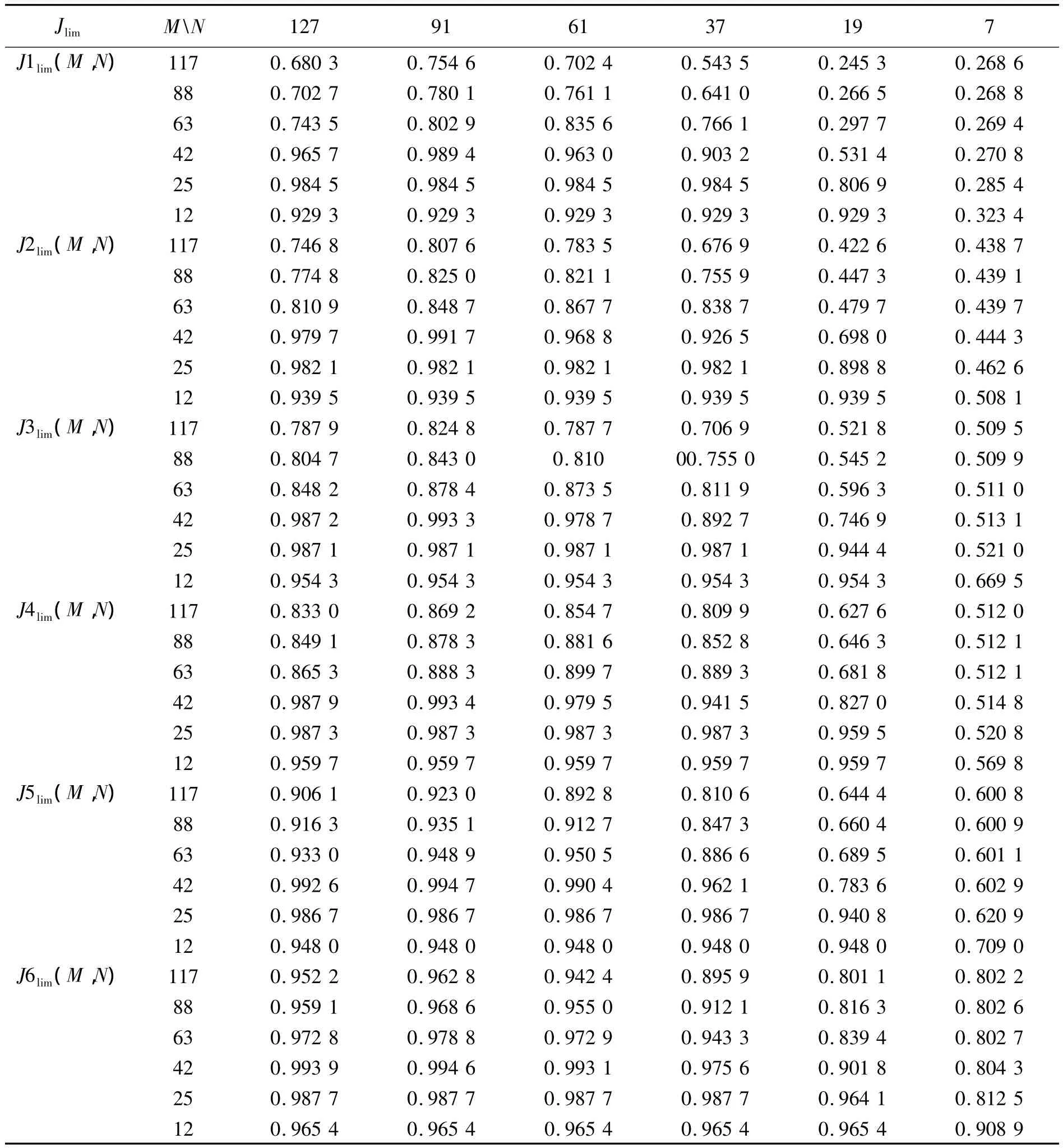
Tab.1 Shaping capability Jlimfor different J0,M and N
4.3 Qualitative and quantitative results of shaping effect of SPGD algorithm
We use RMSlimto measure shaping effect of SPGD algorithm.Shaping effect RMSlimfor different J0,M and N are obtained from expression(15).
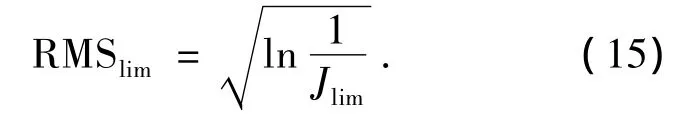
Although its change trend is reverse to that of shaping capability,two results are the same and achieved 6 frames of residual wave-front distribution corresponding to 6 frames of different initial distortion wave-front are shown in Fig.6.Comparisons between Fig.3(a ~f)and Fig.6(a ~ f)indicate SPGD algorithm has good shaping effect.

Fig.6 6 frames of residual wave-front distribution for M=42 and N=91(a:J10=0.0190,b:J20=0.0888,c:J30=0.1601,d:J40=0.2626,e:J50=0.3424,f:J60=0.5265)
5 Discussion
We found that shaping capability and shaping effect respectively are difficult to up to Jlim=1 or RMSlim=0.The reason is that deformable mirror don't shape residual high(117-M)order Zernike aberrations correspondingshown in Tab.2,but low M order Zernike aberrations of initial distortion wave-front.Besides,we can find that SPGD algorithm shapes low M order Zernike aberrations wholly when M≤25 and partly when M≥25,which depends on deformable mirror and parameters of SPGD algorithm.
The change laws of convergence rate,shaping capability and shaping effect about distortion degree of initial wave-front,Zernike order and actuator number of deformable mirror are similar,so expression(14)or(15)can analyze qualitatively the law of convergence rate.Besides,we can select the best deformable mirror for different initial distortion wavefront in atmospheric turbulence form expression(14)or(15).Considering the nature of real-time and simplification of adaptive optics it's better to select 37-unit deformable mirror to shape 3~27(25)order Zernike aberrations at the conditions of some shaping effect.
Tab.2 of 6 frames of initial distortion wave-front only including(117-M)order Zernike aberrations

Tab.2 of 6 frames of initial distortion wave-front only including(117-M)order Zernike aberrations
J10(117-M)1.000 0 0.999 1 0.996 9 0.991 0 0.984 5 0.929 3 J20(117-M) 1.000 0 0.998 7 0.996 1 0.992 4 0.982 1 0.939 5 J30(117-M) 1.000 0 0.999 0 0.996 7 0.993 6 0.987 1 0.954 3 J40(117-M) 1.000 0 0.998 8 0.997 2 0.993 8 0.987 3 0.959 7 J50(117-M) 1.000 0 0.999 3 0.997 8 0.994 8 0.986 7 0.948 0 J60(117-M) 1.000 0 0.999 5 0.995 8 0.994 6 0.987 7 0.965 4 RMS10(117-M)/λ 0 0.004 8 0.008 8 0.015 1 0.019 9 0.043 1 RMS20(117-M)/λ 0 0.005 7 0.009 9 0.013 9 0.021 4 0.039 8 RMS30(117-M)/λ 0 0.005 0 0.009 2 0.012 7 0.018 1 0.034 4 RMS40(117-M)/λ 0 0.005 4 0.008 4 0.012 6 0.018 0 0.032 3 RMS50(117-M)/λ 0 0.004 3 0.007 5 0.011 5 0.018 4 0.036 8 RMS60(117-M)/λ00.003 7 0.010 4 0.011 7 0.017 7 0.029 9
6 Conclusion
In this paper we mainly make detailed simulations for the laws of convergence rate,shaping capability and shaping effectaboutdistortion wave-front,Zernike order and actuator number of deformable mirror of wave-front shaping system with SPGD algorithm for adaptive optics in atmospheric turbulence.We use 6 kinds of deformable mirror as shaping devices and select 6 frames of distortion wave-front including 3~119(117)order Zernike aberrations with Roddier method as shaping objects with SPGD algorithm by selecting appropriate parameters to construct simulation model.The qualitative simulation results show that convergence rate increases with the decrease of Zernike order M,actuator number of deformable mirror N,and distortion degree of initial wave-front decreases.Shaping capability and shaping effect have the same terdency,which increase as Zernike orders M decreases when M≥25 and decrease as M decreases when M≤25,increase as actuator number of deformable mirror N decreases when N≥91 and decrease as N decreases when N≤91,and increase as distortion degree of initial wavefront decreases.Shaping capability and shaping effect are the best when M=42 and N=91.And it can be found from discussion that it's better to select 37-unit deformable mirror to shape 3~27(25)order Zernike aberrations at the conditions of some shaping effect considering the nature of real-time and simplification of adaptive optics system.
[1] WANG S H.Application of stochastic-parallel-gradient-descent adaptive optics techniques in bam cleanup[D].Changsha:National University of Defense Technology,2009.
[2] VORONTSOV M A,CARHART G W,RICKLIN J C.Adaptibe phase-distortion correction based on parallel gradient-descent optimization[J].Optics Letters,1997,22(12):907-909.
[3] VORONTSOV M A,GARHART G W,COHEN M,et al..Adaptive optics based on analog parallel stochastic optimization:analysis and experimental demonstration[J].J.Opt.Soc.Am.A,2000,17(8):1440-1453.
[4] VORONTSOV M.Adaptive photonics phase-locked elements(APPLE):system architecture and wavefront control concept[J].SPIE,2005,5895:1-9.
[5] YANG H Z,LI X Y,GONG C L,et al..Restoration of turbulence-degraded extended object using the stochastic parallel gradient descent algorithm:numerical simulation[J].Optics Express,2009,17(5):3052-3062.
[6] VORONTSOV M A,SIVOKON V P.Stochastic parallel-gradient-descent technique for high-resolution wave-front phasedistortion correction[J].J.Opt.Soc.Am.A,1998,15(10):2745-2757.
[7] YANG H Z,LI X Y,JIANG W H.Simulation and analysis of stochastic parallel gradient descent control algorithm for adaptive optics system[J].Acta Optica Sinica,2007,27(28):1355-1360.
[8] WANG W B,ZHAO S,GUO J,et al..Convergence rate of stochastic parallel gradient descent algorithm based on Zernike mode[J].Chinese Optics,2012,5(4):407-415.
[9] RODDIER N.Atmospheric wavefront simulation using Zernike polynomials[J].Optical Engineering,1990,29(10):1174-1180.
[10] WANG Y R,WANG J Y,XU P,et al..Comparison of experimental analysis of atmospheric coherence length in surface layer[J].J.Atmospheric and Environmental Optics,2010,5(4):263-268.
