基于IR-SFS算法空间目标红外影像3D重建
2014-05-16王汇源刘莹奇张振铎曾子晗
曾 蔚,王汇源*,刘莹奇,王 斌,张振铎,曾子晗
(1.山东大学信息科学与工程学院,山东济南250100;
2.中国科学院长春光学精密机械与物理研究所,吉林长春130033;
3.北京联合大学自动化学院,北京100095)
1 引言
光学成像是获取目标三维模型的重要手段之一,美国麻省理工大学的Horn认为图像的明暗变化隐藏三维信息[1-3],并于1970年提出明暗恢复形状(Shape From Shading,SFS)算法用于 NASA月球表面图像三维重建。传统的SFS算法假设光源为无限远处的点光源或平行光[2],但考虑到红外(Infrared,IR)目标具有自身辐射,灰度明暗变化不仅隐藏三维信息还包括温度信息,在SFS三维重构中的理论模型和具体实现方法有待研究。本文分析了空间目标红外成像特性,建立IR-SFS算法用于红外图像三维重建。
SFS算法是基于单幅灰度图像非接触式三维测量,无需相机标定和目标先验信息,该算法相关的研究主要解决下述问题[4-8]:辐射模型的建立、光照和反射率估计、欠定偏差分方程(Partial Differential Equation,PDE)方程组的解法,以及与其它三维重构方法的融合。其理论的核心思想是电磁波辐射理论与光度学,通过辐射模型将辐射源、辐亮度、物体的几何形状关联在一起,求解辐射方程组可以获得物体表面形状。SFS辐射模型与真实辐射模型相比存在较多的简化处理,比如光源位置和强度估计、反射率估计,欠定PDE方程组病态求解,物体形状的光滑约束,传感器成像过程模型被忽略等等。这样做的结果是,SFS算法的适应性和运算速度极高,但其精度却大打折扣,且数十年来被广泛研究而尚未形成完备的理论和应用体系。
主要的SFS辐射模型有漫反射辐射模型(Lambertian)、镜反射辐射模型(Phong),以及混合辐射模型,这3种经典的模型均只考虑了物体对辐射能量的反射,对于一般的可见光成像来说,这种假设是非常合理的,而对于不透明物体,其表面红外辐射能量是反射辐射和自身辐射的叠加。在红外成像领域对传统的SFS辐射模型进行扩展研究,构建充实完备的理论模型和具体算法,可以提高红外影像三维重建的精度。
上述3种模型中,Lambertian辐射模型应用最广泛,且与远距离暗弱目标成像领域的空间目标表面辐射模型比较相符。本文提出的IR-SFS算法正是对该模型在红外成像领域的理论模型和三维重建实现算法的扩展研究,研究对象是空间目标(包括卫星、航天飞机、空间站等)。为了尽量提高三维重建的精度,详细的理论研究、参数运算和算法设计是必不可少的,研究内容涵盖了:空间目标和地基传感器的坐标变换,外部红外光源的位置和强度的详细分析和计算,自身辐射强度计算,自身辐射对SFS三维重建影响的仿真分析;依据以上理论和仿真分析结果,提出SFS红外温度场概念,利用离散余弦变换(DCT)估计温度场形状,通过自身红外辐射能量和反射辐射能量的比例系数,获得红外差值图,然后进行三维恢复。一系列分析和计算,虽然算法比较复杂,但实验结果可获得更高的信噪比,验证了算法的有效性。该算法不能像立体视觉的方法那样获得尽可能高的模型精度,对于空间目标红外成像来说,立体视觉的方法难以实现。
本文第二部分讲述传统的SFS算法;第三部分分析空间目标红外成像特性并建立IR-SFS辐射模型;第四部分为IR-SFS辐射模型仿真分析;第五部分为IR-SFS算法说明;第六部分为实验结果和分析;第七部分为全文的总结。
2 传统的SFS算法
传统的SFS算法一般假设目标为朗伯体,表面光滑连续;存在唯一光源,发出平行光。其归一化表面辐射图和归一化灰度图相等,辐射方程为:
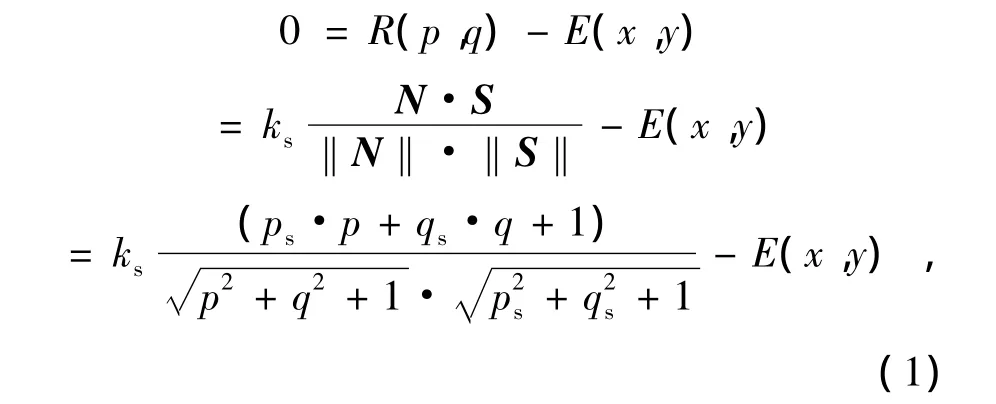

3 空间目标红外成像特性分析
参照传统SFS算法,空间目标红外成像特性分析的假设条件为:
(1)目标为朗伯体,表面光滑连续,在成像波段内有单一的反射率和发射率;
(2)外部辐射包括:太阳辐射、大气和地球反照的太阳辐射、地球红外辐射;
(3)目标具有温度场,发出自身红外辐射。
3.1 理论基础
在上述假设条件的基础上,展开红外辐射的基础理论分析,然后结合传统SFS算法的辐射模型,推导出IR-SFS辐射模型方程。
(1)坐标系
坐标系如图1所示,地平坐标系O-XYZ以传感器为原点,正东为X轴,正北为Y轴,天顶为Z轴,成像时的偏角和仰角为α和β;目标坐标系OXYZ以目标为原点,两者齐次坐标变换矩阵H如式(2)。传感器观测参数以前者为参考;三维模型Z=Z(x,y)以后者为参考。

图1 坐标系Fig.1 Coordinates

(2)外部辐射和自身辐射
太阳辐射Q1,大气和地球对太阳辐射的反照辐射Q2,地球红外辐射Q3,如式(3)~(5);自身辐射Q4如式(6)[9]。

式中,dA为微面元,ρ为反射率,ε为发射率,S为太阳辐射常数,γ1、γ3为成像波段因子,R为地球半径,h为轨道高度,λ为大气透过率;Q'4为等效黑体辐射强度,由温度T和成像波段[λ1,λ2]根据普朗克辐射定律、斯蒂芬-玻尔兹曼定律计算获得;Fs为成像类型因子,FΩ为大气和地球反射因子;F1、F2、F3、F4为形状因子,采用蒙特卡洛方法计算获得,基本计算式如式(7)~(10)。
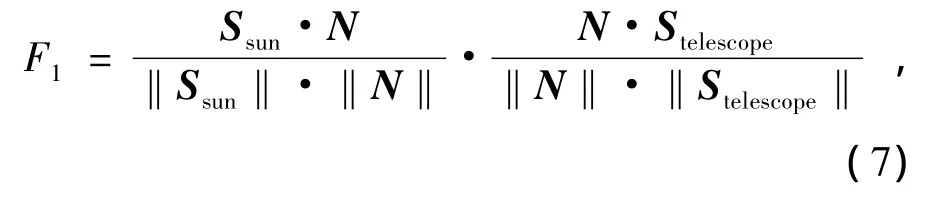

3.2 建立IR-SFS辐射方程
综合上述理论得红外辐射图Q=Q1+Q2+Q3+Q4,根据传统SFS辐射理论O=Q(x,y)-E(x,y),整理并离散化得IR-SFS辐射方程:

式中:c1是第一辐射常数;c2是第二辐射常数;σ是斯蒂芬-玻尔兹曼常数;T(i,j)是热力学温度场图。
4 IR-SFS辐射方程仿真分析
式(11)所示IR-SFS辐射方程与式(1)所示传统SFS辐射方程的差异在于ζ4(i,j)项。下面考虑两种情况分析它对目标几何形状的影响:(1)ζ4(i,j)=0,即自身辐射为 0,只考虑目标对外界辐射的反射,此时对应传统SFS算法的辐射模型;(2)ζ4(i,j)≠0,即自身辐射不为 0,同时考虑目标对外界辐射的辐射以及目标自身辐射,对应本文提出的IR-SFS辐射模型。三维重建过程中,欠定PDE方程组求解方法采用Ping-Sing Tsai and Mubarak Shah 的线性化方法[7],Newtong-Raphson迭代次数20次。
4.1 第一种情况 ζ4(i,j)=0
灰度级为L的图像中两相邻微面元dA1、dA2(如图2(a)),灰度值(g1,g2),光源矢量(0,0,1)。

图2 微面元dA1与dA2的灰度图和三维模型Fig.2 Gray image and 3D model of microfacet dA1,dA2
将各参数代入式(1),利用Tsai方法求解出三维模型见图2(b)。其中dA1,dA2在三维模型中梯度(p1,q1)、(p2,q2)为q1=q2=p1=0,p2=|z1-z2|。法向矢量夹角θ为:

仿真参数:L=8,g1=0,g2=0∶255 递增。
仿真结果:求得θ变化曲线如图3所示,其中最小、最大值分辨角分别为 θmin=0.81°和θmax=74.47°。
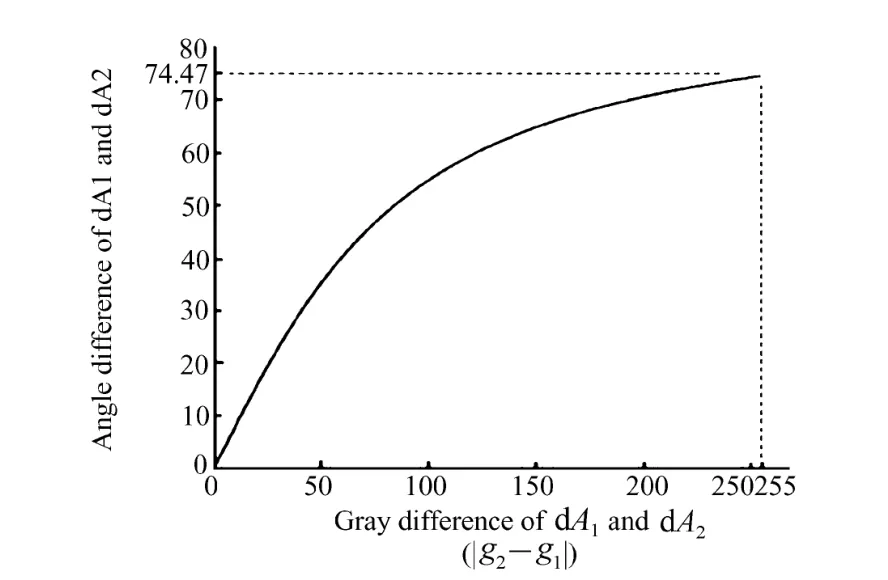
图3 仿真结果曲线[ζ4(i,j)=0,dA1和dA2的夹角为θ]Fig.3 Simulation results[ζ4(i,j)=0,θ is the angle between dA1and dA2](calculated by Tsai method)
仿真结果分析:像素间灰度差异越大,法向矢量角度越大,若像素灰度值变化则会导致三维形状失真;最大分辩角仅为74.47°,无法表示大于该角度的几何形状,这也是“假设物体表面光滑”的理论依据。
4.2 第二种情况 ζ4(i,j)≠0
第二种情况,分析ζ4(i,j)>0对三维重构模型的影响,即θ的变化情况。
假设条件:目标前景的温度和发射率一致,自身辐射强度等效灰度值ζ4(i,j)>0。不失一般性灰度级取值为L=8,前景灰度范围从(0,255)变为(0+ζ4,255+ζ4),背景灰度范围仍为(0,255)。dA1,dA2在新图像中灰度值(g'1,g'2)=[255·(g1+ζ4)/(255+ζ4),255·(g2+ ζ4)/(255+ζ4)],θ的新值为 θ'。
仿真参数:取 ζ4=0∶100∶10 000,g1=0,g2=0∶255。

图4 仿真结果曲线[ζ4(i,j)≠0,dA1和dA2的夹角θ']Fig.4 Simulation results[ζ4(i,j)≠0,θ'is the angle between dA1and dA2](calculated by Tsai method)
仿真结果:θ'的变化见图4(a);峰值信噪比(PSNR)估计见图4(b)。随着自身辐射的增强,角度估计值逐渐恶化,见表1;当ζ4=50时,最大角度失真达到2.76°;当ζ4=500时,最大角度失真达 23.92°。
仿真结果分析:自身辐射对三维模型有弱化效应,弱化程度与信噪比有关;随着温度逐渐升高弱化效应是渐变的。

表1 仿真结果Tab.1 Simulation results
5 基于IR-SFS三维重建算法
基于上述研究,提出针对空间目标红外影像三维重建的IR-SFS算法。
首先,根据已知条件进行目标红外成像特性分析,计算目标、太阳、地球的相互位置关系,外部辐射强度。其次,提出渐变温度场概念,温度场信息隐藏在图像的低频区域;通过DCT变换和低通频域滤波器H(i,j)得到温度场,利用普朗克辐射定律、斯蒂芬-玻尔兹曼定律计算其等效辐射强度,按照能量比例因子获得归一化自身辐射图ζ4,进而得红外差值图[E(i,j)- ζ'4(i,j)]。然后,根据Tsai方法求解目标三维模型。最后,根据SFS评价因子EQ1(收敛性)、EQ2(收敛到预期值)、EQ3(运算速度)、EQ4(鲁棒性)、EQ5(主观评价)对算法结果进行分析。
此外,基于温度场估计需要对温度场类型(即滤波器类型)、温度范围和温度场半径进行估计,不同的估计值会得出不同结果。因此,增加评价因子EQ6,即在不同的参数设定下,计算目标反射辐射和自身发射辐射强度,以及三维模型的截面周长、截面积、曲面面积、体积、平均高度和最大高度的等效估计值。本文提出的IR-SFS算法流程如图5(a)所示;传统的SFS算法并没有考虑红外影像中目标自身辐射,如果将其直接应用于红外影像则没有第二、三、四个环节,其算法流程如图5(b)所示。
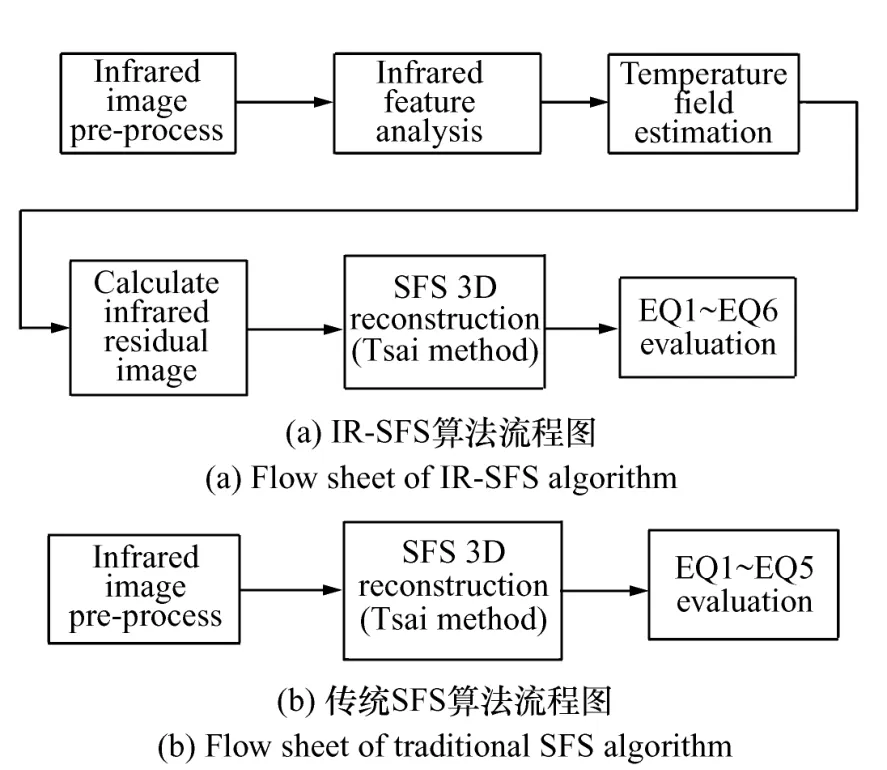
图5 算法流程图Fig.5 Flow sheet of IR-SFS algorithm and traditional SFS algorithm
5.1 温度场估计
温度场属于低频分量,通过低频滤波器提取温度场的空间分布特征,并根据前述的空间目标红外特性分析将温度场映射到合理的强度,获取红外差值图。
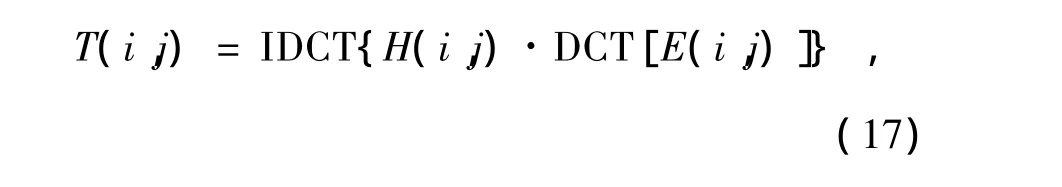
下式为温度场空间分布特征估计方法:式中:DCT是离散余弦变换;IDCT是离散余弦逆变换;H(i,j)是频域低通滤波器;T(i,j)是温度场估计值。限于本文的篇幅和研究重点,仅选用以下3种常用低通滤波器[13-16]进行算法测试:

式中:RT是温度场滤波器截止频率,σ1,σ2是温度场高斯低通滤波器方差,均称之为温度场半径。
5.2 红外差值图
经过前述红外特性分析获得外部辐射系数ζ1、ζ2、ζ3和温度场T(i,j),然后根据普朗克辐射定律、斯蒂芬-玻尔兹曼定律计算辐射强度,并归一化为ζ4(i,j),根据式(21)得到红外差值图:

5.3 评价因子EQ6

式中,Ω表示ROI区域,Ω'表示Ω的八连通边界。由于该算法的三维模型高度无量纲,EQ6对测试算法具有参考价值,但不都代表绝对物理量;如果高度信息经过标校的话,会具有较好的实际含义。
6 实验结果及分析
算法程序用 Matlab7.0在 Intel i5-3470的CPU,4GB内存的计算机上实现。图6为进行算法测试的STS107红外影像[10],它是“哥伦比亚航天飞机失事前四天,利用3.67 m望远镜长波红外摄像机获得的高清晰图像”[11],目标信息见表 2[10,12]。

表2 STS107目标参数Tab.2 Parameters of target STS107
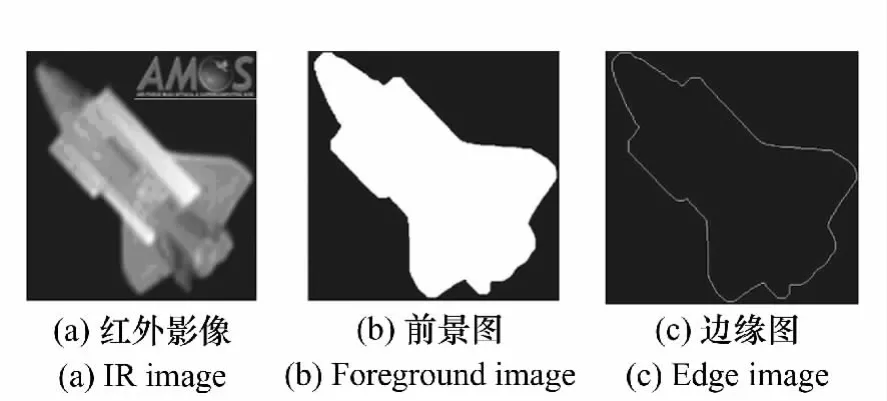
图6 STS107目标图像Fig.6 Image of target STS107
为描述方便,测试参数温度场估计滤波器、温度场半径、温度估计范围和迭代次数,分别以TF、TR、TD和Iter表示。由于缺乏STS107目标的真实三维模型,难以对重建结果进行客观评价,我们首先对人工合成的红外目标的红外影像进行算法测试。
6.1 人工合成目标实验
分别利用SFS算法和IR-SFS算法对人工合成的球体、圆柱体卫星的红外影像进行三维重建,比较两者重建模型的视觉效果、与真实模型的差值和峰值信噪比。
(1)合成球体卫星
假设存在一球体空间目标,半径r=10 m,我们能观察到卫星的一侧,其曲面方程为:

表面梯度为:

人工合成目标的条件和方法:假设成像类型是地影成像,等效红外光源矢量(0,0.15,1),轨道高度为280 km,卫星蒙皮反射率为0.7,成像波段为8.3~9.2 μm,大气透过率为0.45,根据式(12)~(14)计算出目标反射外界辐射平均强度为3.76 W/m2;卫星温度为250~400 K的随机值(本文测试值为300 K),红外发射率为0.3,只考虑成像波段内的红外辐射,根据式(14)计算出平均辐射强度为3.41~41.00 W/m2;根据式(28)、(29)生成理想球体卫星模型见图7(a、b),根据式式(11)、(21)合成的卫星红外图像如图7(c)所示。

图7 球体卫星图Fig.7 Images of hemi-sphere satellite
分别采用传统的SFS算法、本文提出的IRSFS算法对图7(c)表示的目标红外影像进行三维重构,其中欠定 PDE方程组求解方法采用Ping-Sing Tsai and Mubarak Shah的线性化方法[7],Newtong-Raphson迭代次数 20次。SFS算法测试参数Iter=20,生成三维模型见图8(a),与真实模型的差值图见图8(b);IR-SFS算法测试参数 TF=H3,TR=20,TD=250 ~350 K,Iter=20,生成三维模型见图8(c),与真实模型的差值图见图8(d);由于已知真实的三维模型,可以计算出迭代过程中的PSNR,见图9。

图8 球体卫星红外图三维重建模型Fig.8 3D reconstruction results of hemi-sphere satellite

图9 球体卫星红外图三维重建实验PSNRFig.9 3D reconstruction PSNR of hemi-sphere satellite
结果分析:从图8、9可以看出两种算法都可以重建出目标的三维模型,并且都存在一定的误差。进行比较发现:原SFS方法虽然也能收敛,但是由于没有考虑目标自身辐射对三维重建的影响,迭代过程中信噪比仅为5.3 dB左右;而本文IR-SFS算法一定程度上考虑了自身辐射,虽然没能完全消除误差,但是随着迭代过程误差减小的更快,PSNR比原SFS算法提高约13 dB。
(2)合成圆柱卫星
假设存在一个圆柱形的卫星,尺寸底半径r=4 m、高h=10 m,传感器能观察到目标的一侧,其曲面方程为:
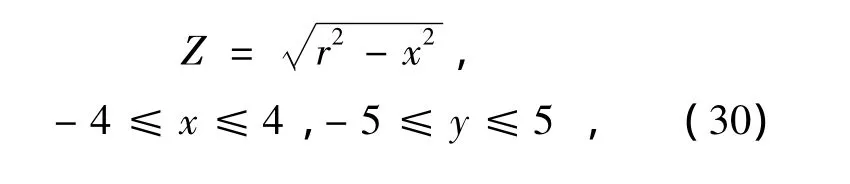
表面梯度为:

人工合成目标的条件和方法与前述球体卫星一致。理想半圆柱体卫星平面图见图10(a),其三维图见图10(b),红外图像见图10(c)。目标实际温度为恒定的300 K,在IR-SFS算法中估计目标温度为250~400 K,而SFS算法中忽略目标温度,因为目标的真实温度往往是未知的,IR-SFS算法通过对目标的红外特性分析,大致已知了其真实温度范围,理论上来说更逼近真实温度值;传统的SFS算法重建的三维模型、以及误差图见图11(a)、11(b),本文的IR-SFS算法重建的三维模型和误差图分别见图11(c)、11(d)。迭代过程中,与真实模型的PSNR,见图12。结果分析:从图11、12可以看出两种算法都可以重建出目标的三维模型,并且都存在一定的误差。进行比较发现:虽然新方法没能完全消除误差,但是较原SFS方法PSNR提高约25 dB。

图10 圆柱卫星Fig.10 Images of cylindrical satellite

图11 圆柱卫星红外图三维重建模型Fig.11 3D reconstruction results of cylinder satellite

图12 球体卫星红外图三维重建实验PSNRFig.12 3D reconstruction PSNR of cylinder satellite
6.2 STS107三维重建实验一
通过人工合成目标的仿真实验,验证了新算法在一定程度上提高了重建三维模型的准确度。下面在空间目标STS107真实红外影像上进行三维重建实验。

图13 实验结果Fig.13 Test results
初步测试参数:TF=H1,TR=50,TD=200~300 K,Iter=15。测试结果如图13所示,可以看出,红外差值图目标细节比原图有所改善,重建模型对目标各部位的细节表现丰富。
结论和分析:由温度场估计获得的红外差值图重建的三维模型具有较好的显示度。
6.3 STS107三维重建实验二
这部分详细地介绍三维重建实验以及实验分析。评价因子包括EQ1~EQ6,以及 SFS和 IRSFS效果对比。根据本文的重点,对EQ5、EQ6实验进行了较详细的说明。
(1)SFS和 IR-SFS的 EQ1、EQ2、EQ3对比实验
SFS 实验参数:Iter=50,光照方向(0,0,1);IR-SFS实验参数:TF=H1、H2、H3,TR=50,TD=200~350 K,Iter=50。
由于缺乏目标的真实模型作为参考,收敛均方误差(MSE)值为相邻两次迭代的均方误差;PSNR的参考模型是最后一次迭代的三维模型。

图14 SFS与IR-SFS的MSE和PSNR对比Fig.14 MSE and PSNR of IR-SFS compared with SFS
实验结果 MSE见图14(a),PSNR见图14(b),从图中可以看出IR-SFS较SFS均具更佳的收敛性。第50次迭代误差从2.58e-004减小为1.85e-5;PSNR统计平均提高11.47 dB;50次迭代的对比实验共耗时约12 s,能满足非实时数据处理的一般要求。
(2)鲁棒性评价(EQ4)
图15(a)为被高斯噪声污染的目标红外影像,图15b为经过中值滤波的影像,图15(c)为重建结果。重建的三维模型具有一定的主观评价,目标的机翼、机舱、尾翼等的三维模型均被明显重构出来,说明算法对噪声具有一定程度的鲁棒性。由于本文算法实质是考虑目标自身辐射作为一种噪声对SFS三维重构的影像,其它形式的噪声对SFS算法的鲁棒性影响将在后续论文中深入研究。
(3)主观评价(EQ5)

图15 EQ4测试Fig.15 Test results of EQ4
测试参数:TF=H1、H2、H3,TR=10、50,TD=200~280 K、200~350 K,Iter=15。

图16 IR-SFS三维重构图(TF=H1或H2或H3,TR=10或50,TD=200~280 K或200~350 K)Fig.16 3D models of IR-SFS algorithm(TF=H1、H2、H3,TR=10、50,TD=200 ~ 280 K,200 ~350 K)
测试结果:三维模型见图16,其中图16(a,b,c,d)为 TF=H1 产生的三维模型,图16(e,f,g,h)为 TF=H2 产生的三维模型,图 16(i,j,k,l)为TF=H3产生的三维模型,图下标3个参数分别表示TF、TR、TD的取值。将SFS算法直接应用于红外图像,得到的三维模型如图17所示。分析:从图16可以看出,滤波器为H1、H3,温度场半径等于50时,航天飞机顶部舱门、尾翼、机舱内方形部件具有较佳显示度;滤波器为H2,温度场半径等于10时,航天飞机机舱空间有明显凹陷感;SFS算法能重建出目标的三维模型,对各部分也具有显示度;对比两种算法对目标不同部件的表现度,如飞机尾翼的形状,机舱内方形部件形状,顶部两侧机翼的形状,主观比较之下新算法对目标细节的显示效果有所优化。

图17 SFS算法重建的三维模型Fig.17 3D model obtained with SFS algorithm
结论:IR-SFS算法参数 TF、TR 、TD、Iter的优化能表现出目标的不同特性,较SFS算法对目标细节的表现力有所改善。
(4)温度递增实验(评价因子EQ5和EQ6)
分别对TF=H1、H2、H3 3种温度场估计滤波器进行测试,由于对TF=H2、H3进行的测试结果与TF=H1基本一致,在此仅对TF=H1的情况进行说明。
测试参数:TF=H1,TR=50,TD=200 ~220∶1∶1 000 K,Iter=20。EQ6 测试结果见图 18,以及重构三维模型见图19。
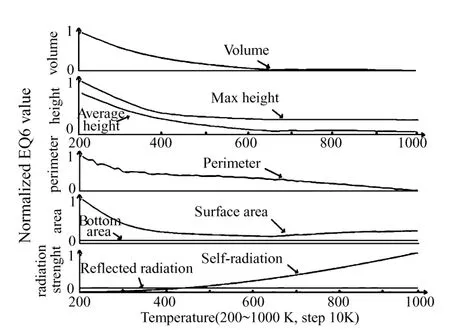
图18 EQ6(温度递增实验)的测试结果Fig.18 Test results of EQ6 with TD increasing
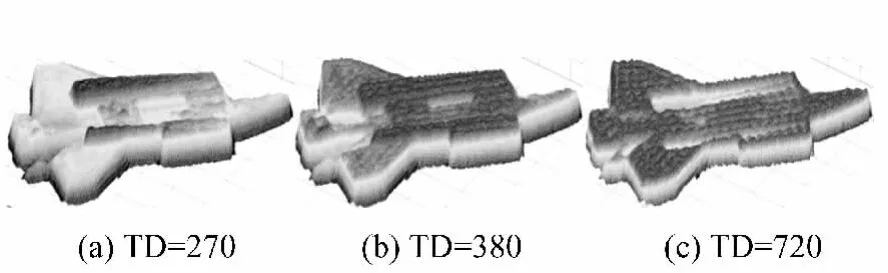
图19 温度递增实验三维模型Fig.19 3D models with TD increasing
分析:随着温度升高,自身辐射强度增大,几何形状参数不断减小,三维模型的主观评价在TD=380左右逐渐下降。
结论:温度估计差异对EQ6具有较大影响,不易获得稳定值;对于当前样本,温度估计为200~380 K时,3D模型具有较好的主观评价,这与文献[10]中对空间目标的实际温度范围估计一致。
(5)温度场半径递增实验(评价因子EQ5和EQ6)
测试参数:TF=H1、H2、H3,TR=1∶1∶455,TD=200~350 K,Iter=15。
TF=H1、H2、H3时的EQ6评价结果基本一致,在此仅将TF=H1的EQ6测试图列在图20中;TF=H1、H2、H3时重建的三维模型分别见图21、22、23,分别进行主观评价。

图20 EQ6(温度场半径递增实验)的测试结果Fig.20 Test results of EQ6 with TR increasing

图21 温度场半径递增实验三维模型(TF=H1)Fig.21 3D model with TR increasing at TF=H1
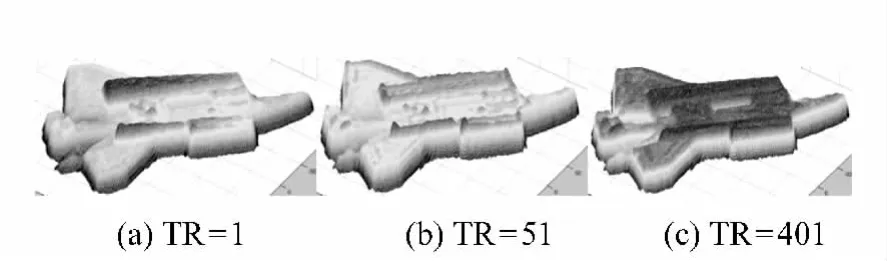
图22 温度场半径递增实验三维模型(TF=H2)Fig.22 3D model with TR increasing at TF=H2

图23 温度场半径递增实验三维模型(TF=H3)Fig.23 3D model with TR increasing at TF=H3
分析:当温度场半径小于50时,EQ6各参数存在极大值、极小值,目标不同细节的表现度差异较大;当温度场半径大于50时,EQ6参数趋于稳定,模型的形状变化不大,并且对航天飞机船舱、尾翼、机翼具有较好的细节表现度。
结论:通过优化温度场半径可以获得目标稳定的三维模型,且具有较好的主观评价,当前目标的TR优化参数为50。
7 结语
本文将SFS算法扩展为IR-SFS算法,建立了IR-SFS辐射模型和三维重建算法,并进行了仿真分析,在此基础上对合成球体、圆柱体卫星和真实的空间目标STS107的红外影像进行了算法验证。对于STS107红外影像,当参数优化为温度范围估计TD=200~350 K、温度场半径TR=50、迭代次数大于Iter=15次时,目标的顶部舱门、尾翼、机舱、机舱内的方形部件具有较好的显示度,算法的收敛性、信噪比和三维模型的主观评价较原SFS算法有一定程度的改善。在今后工作中,要对温度场估计方法和参数优化进行深入研究,比如滤波器的设计,温度场半径的选取,温度范围的设定方法等。
[1] HORN B K P.Shape from shading:a method for obtaining the shape of a smooth opaque object from one view[D].Boston:Massachu-setts Institute of Technology,1970.
[2] HORN B K P.Obtaining Shape from Shading Information[M].Cambridge:MIT Press,1989.
[3] HORN B K P.The Variational Approach to Shape from Shading[M].Cambridge:MIT Press,1989.
[4] ZHANG R,TSAI P S,CRYER J E,et al..Shape from shading:a survey[J].Pattern Analysis and Machine Intelligence,1999,8(21):690-706.
[5] DANIEL P,DENIS J.From deterministric to stochastic methods for shape from shading[C].Asian Conference on Computer Vision,Taipei,Taiwan,China:ACCV2000,2000:187-192.
[6] DUROU J D,FALCONE M,SAGONA M.Numerical methods for shape-from-shading:a new survey with benchmarks[J].Computer Vision and Image Understanding,2008,109(1):22-43.
[7] ZHENG Q F,CHELLAPPA R.Estimation of Illuminant Direction Albedo and Shape from Shading[C].Proceedings CVPR'91.,IEEE Computer Society Conference,Maui,Hawaii,3-6 Jun 1991.
[8] TSAI P S,SHAK M.Shape from shading using linear approxiamation[J].Image and Vision Computing,1994,12(8):487-498.
[9] WU X D,HUANG CH CH,LING Y SH.Surface temperature and infrared feature of a satellite[J].Infrared and Laser Engineering,2011,40(5):805-810.
[10] TOMBASCO J.Air force Maui optical& supercomputing site tutorial[C].AMOS 2006 conference proceedings,Hawaii,USA,2006:979-972.
[11] 王建立,陈涛,张景旭.地基高分辨率光电成像望远镜总体需求及关键技术分析[J].光学 精密工程,2008,5(16):1-16.
WANG J L,CHEN T,ZHANG J X.General requirement and key technologies for the ground-based high resolution EO imaging telescope[J].Opt.Precision Eng.,2008,5(16):1-16.(in Chinese)
[12] 张景旭.国外地基光电系统空间目标探测进展[J].光学 精密工程,2008,5(16):17-23.
ZHANG J X.Progress of foreign space target detection using the ground-based optoelectronic tracking system[J].Opt.Precision Eng.,2008,5(16):17-23.(in Chinese)
[13] . [J]. ,2011,4(5):503-508.
LIU W N.Dim target detection based on wavelet field diffusion filter[J].Chinese Optics,2011,4(5):503-508.(in Chinese)
[14] 靳永亮,王延杰,刘艳滢,等.红外弱小目标的分割预检测[J].光学 精密工程,2012,20(1):171-178.
JIN Y L,WANG Y J,LIU Y Y,et al..Pre-detection method for samll infrated target[J].Opt.Precision Eng.,2012,20(1):171-178.(in Chinese)
[15] 邓建青,刘晶红,刘铁军.基于DSP系统的超分辨率图像重建技术研究[J].液晶与显示,2012,27(1):114-120.
DENG J Q,LIU J H,LIU T J.Super-resolution image reconstruction technology based on DSP system[J].Chinese J.Liquid Crystals and Displays,2012,27(1):114-120.(in Chinese)
[16] 王娴雅,陈钱,顾国华.基于灰度相关的高分辨率红外图像重建[J].光学与光电技术,2009,7(2):33-36.
WANG X Y,CHEN Q,GU G H.High resolution infrared image reconstruction based on pixel gray correlation[J].Optics Optoelectronic Technology,2009,7(2):33-36.(in Chinese)
