动力煤期货价格预测模型
2014-11-26张智勇李宏军李冬武
张智勇 李宏军 杨 鹏 李冬武
(1.中国中煤能源股份有限公司销售中心,北京市西城区,100120;2.国务院研究室,北京市西城区,100017;3.中国矿业大学 (北京)管理学院,北京市海淀区,100083)
1 动力煤期货价格预测方法选择
无论是煤炭产业链上下游企业套期保值操作,还是进行投机获利,对期货价格进行合理的预测都是非常重要的。金融市场上价格预测的方法很多,如技术分析和基本面分析等,侧重点各有不同。动力煤期货上市时间不久,对其价格的预测多出于经验判断,得出的一般是相对模糊的结论,且容易受到人自身情绪的干扰,难以做到客观理性。
对于商品期货市场来说,一般都具有相对透明、自由流通、资金量巨大的特征,参与者基本都是价格的被动接受者,接近完全自由市场,因此适宜建立数量模型对价格进行预测。
本文并非简单的理论探讨,而是从最大化实用的角度出发,使用计量经济学VAR模型方法,建立动力煤期货价格预测模型。既要符合正确的理论,又要方便应用,实现对动力煤期货价格走势的理性判断。
2 模型变量的选择
2.1 变量的选择范围
动力煤期货的价格与动力煤的生产、运输、需求、库存、进出口等因素直接相关,也与我国的宏观经济情况息息相关。因此在建模过程选择与动力煤产业链相关的产、运、需、存相关因素,以及宏观经济因素作为模型的备选变量;此外,考虑到股票市场是国民经济的晴雨表,对宏观经济变化具有先行的特点,因此将沪深300指数与上证180指数纳入变量考虑范围,见表1。

表1 动力煤期货价格建模备选变量
煤炭行业个别数据有部分缺失 (尤其是12月份和1月份数据),一些缺失数据可由同期增长数据计算得出,无法获取的数据我们使用三次样条插入法来补足,使用Matlab软件编程计算。
2.2 期货历史价格的模拟
由于动力煤期货目前上市时间太短,没有足够的动力煤期货历史价格数据序列,因而在建立动力煤期货价格预测模型时,想要预测的变量的数据就没有来源,难以建模。考虑到期货与现货当期价格之间具有较大相关性,在参数估计时使用环渤海动力煤价格指数 (BSPI)替代期货的历史价格。
环渤海动力煤价格指数基本能综合反映动力煤的现货价格,而现货价格与期货价格的高度相关性,在期货市场上广泛存在,尤其是比较大的品种和比较成熟的品种,这种高度相关性在理论上也完全成立,这是由期货的交割机制决定的。比如国际原油现货价格与WIT原油期货价格的相关系数达到0.99。随机选取几个中国的期货品种,发现与现货价格相关性系数都较大。如太原螺纹钢期现货相关性系数为0.943,沪铜1311期货与现货相关性系数为0.934。
2.3 变量的筛选检验
表2中所列变量是一个选择范围,并不是全部选择。有些变量因素,主观上认为是动力煤市场产业链的重要因素,但由于市场的复杂性,经过系统的多次传导,该因素是否与最终的价格密切相关,主观的判断就不太可靠,需要通过数据统计检验来说明。通过相关性检验保留影响动力煤价格变化的最重要因素,剔除与之相关性较小的、对于前瞻性预测无作用的因素,使模型尽可能准确地预测动力煤价格变化。
在分析时间序列数据时,使用传统的相关性检验容易出现伪回归问题,因此要求变量之间存在协整关系以避免这个问题。对于我们这里的检验来说,主要目的只是为了实现筛选出有用变量、剔除无价值变量。由于伪回归是回归的必要不充分条件,且VAR模型对协整性没有要求,因此可以不考虑伪回归的问题。
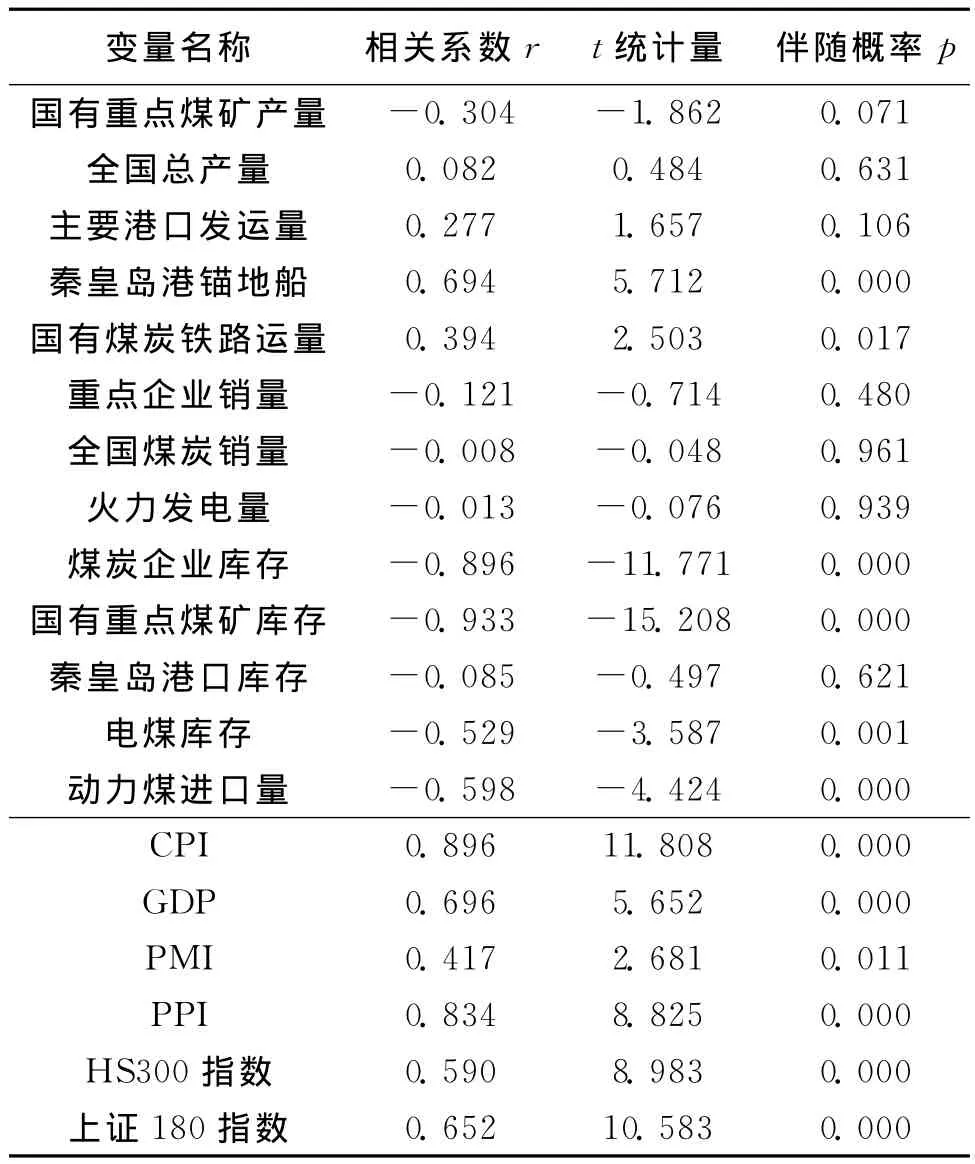
表2 变量的筛选检验
将前文所述每一个变量分别与环渤海指数做相关性检验,相关性较小的则剔除考虑范围。最终选取秦皇岛锚地船数量、国有煤炭铁路运量、国有重点煤矿库存、电煤库存、动力煤进口量、PPI、CPI、HS300指数作为模型变量。由于沪深指数与上证指数相关性非常高,达到0.994,因此只选取其中一个,用沪深指数作为变量即可。煤炭企业库存和国有重点煤矿库存的相关性也很高,达到0.90,只保留与环渤海指数相关度更高的国有重点煤矿库存。另外,GDP数据是以季度为时间单位发布的数据,我们的模型是月度预测模型,如果把GDP纳入变量,实际预测使用起来不太方便,因而舍去。
3 动力煤期货价格预测模型
3.1 模型形式及基本解释
本文建模的主要目的是为预测动力煤期货的价格,对价格形成原因的诠释则放在次要位置,使用Eviews_6.0作为计量经济计算软件,同时使用Matlab(R2012a版本)辅助计算。
TCFutures:动力煤期货价格,即Thermal CoalFutures;TCFutures(-2)为动力煤期货价格上2期 (滞后2期,上上个月)的值,TCFutures(-3)为动力煤期货价格上上一期 (滞后3期,往前推3个月)的值。其余变量与此类同。
3.1.1 时间单位
由于信息化的发展,通过金融交易平台,我们可以实时观察到价格变化,最小精确到秒,还可以是年、月、周、日、时、5分钟等。但是,考虑太小时间单位内的价格变动有时候是没有意义的。价格是市场参与主体对各类信息的综合反应,太小时间单位内的变动经常是属于 “市场噪音”,没有什么规律可循。即使勉强做出预测模型,其效果衰减的速度也会很快。
适当长的时间的价格变动,比如月、年,就有一定意义了,能够比较好地研究市场规律。如果时间周期更长,比如10年、20年,或许有意义,但对于参与主体来讲,应用价值较小。
对于我们的模型来说,预测周期是月。选择以月为单位主要原因是多数统计数据是按月发布的,对企业参与套期保值来说也更具操作意义。实际使用时,将变量的统计数据值带入模型,即可得出模型对当月价格的预测,这一预测值是当月价格的平均值。
3.1.2 模型阶数
VAR模型阶数太多会导致变量太多,模型自由度太大,根据建模经验,参考AIC、SC原则,最终确定为2阶。从动力煤价格模型预测实用的角度出发,本文对模型做以下调整:
(1)国有煤炭铁路运量、国有重点煤矿库存、电煤库存、动力煤进口量、PPI、CPI这几个变量的数据发布滞后时间比较长,有些常常滞后超过1个多月。我们使用-2和-3期两阶。如果采用-1期的话,则实际预测时有可能还没有发布。
(2)秦皇岛锚地船数量、HS300指数这两个指标的数据发布比较及时,采用-1和-2期两阶。
但是VAR模型变量必须是同阶的,所以输入变量的数据时间序列时,就把不同阶的数据序列提前或滞后一期输入,这样就能实现不同阶的VAR模型。经过这样的调整,模型在实际测算时就能确保可有效获取数据,带入前期数据求出下个月期货价格的预期增长量,预期增长量加本月的实际价格,就能求出下个月期货的预期价格,实现预测的目的。
3.2 模型结果
建立VAR模型前,首先对所有变量取差分运算。Eviews软件中,差分运算公式是D(y)=y-y(-1),其经济意义相当于环比增长。
所建立的动力煤期货价格预测模型如下:
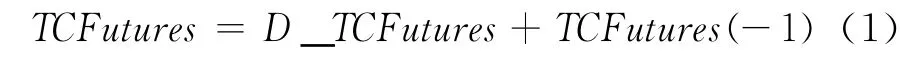
式中:TCFutures(-1)——某月前一个月期货平均价格,可以查看统计数据或金融数据终端得到;
D_TCFutures——某月期货价格理论差分值,也就是由模型计算得出的理论环比增长值;
TCFutures——某月的理论期货价格,也就是我们对此月期货价格的预测值,由上式相加得出。
其中:

式中:
D_CPⅠ——消费物价指数环比增长量;
D_HS300——沪深300股票指数环比增长量;
D_ⅠMPORT——动力煤进口量环比增长量;
D_PPⅠ——生产者物价指数环比增长量;
D_QB——秦皇岛港锚地船数量环比增长量;
D_STMK——国有重点煤矿库存环比增长量;
D_STPOWER——电煤库存环比增长量;
D_TRR——国有煤炭铁路运量环比增长量;
可以注意到,秦皇岛锚地船数量和HS300指数这两个变量的滞后期数是-1和-2,其余变量的滞后期数是-2和-3。
VAR模型稳定性检验的原则是:AR根的模都小于1,且位于单位圆内。符合这一条件的说明构建的VAR模型是稳定的。本模型的AR根检验结果见图1。

图1 模型的稳定性检验
从图1可见,所有的点落于单位圆内,即AR根的模都小于1,说明模型是稳定的。
模型计算完成后,把变量数据带入模型,回测出期货价格,与历史数据作对比,以检验模型的效果。模型回测值与历史价格数据的对比见图2,可以看到,模型回测的值与历史数据非常吻合,可以直观了解到该模型的预测效果是比较理想的,相关性系数达到0.997以上。模型回测数据与历史数据的残差值见图3,可见残差值较小,大致介于-12和14之间,标准差为9.3567,波动较小,且很接近随机正态分布,说明信息挖掘比较彻底,也是比较理想的。
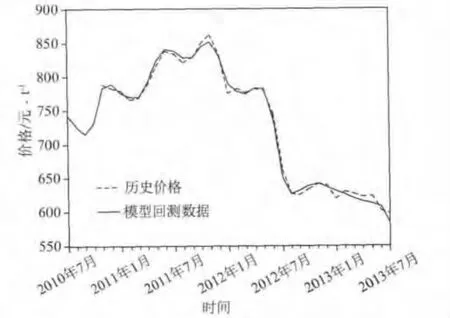
图2 模型回测值与历史价格数据的对比
回测值与历史数据的相关性检验结果为:相关系数0.997,t统计量75.33,p值0.00。

图3 预测残差的分布
残差的描述性统计结果为:最大绝对值13.79,均值0.418,标准差6.57,J-B值0.95。
3.3 模型的相关说明
3.3.1 模型应用
本文模型是用环渤海指数代替动力煤期货价格估计参数的,因此在动力煤上市初期会存在难以避免的基差。由于没有更好的能反映动力煤价格走势变化的统计数据,在误差较小的情况下,模型仍很有参考意义。经过验证,使用本模型来预测动力煤期货价格趋势完全可行,可以准确预测出上市初期的涨势。
3.3.2 突发事件因素
本模型考虑的是普通情况下的市场,没有考虑到突发状况。在发生金融危机或重大经济环境变化时,由于原有的市场规律会突然失效,陷入混乱,模型也会坍塌而失去预测效果,此时应该暂停使用模型,需要等待危机的消退重新预测。此时若要进行市场预测,可以考虑以基本面分析方法为主。
3.3.3 模型效果的衰减
本文模型是以历史数据为基础建立的,因此,模型所述的表达式能代表一定时期的市场内部规律。随着时间的推移,模型的预测效果会逐渐衰退,偏离逐渐变大,在时间足够长之后,原有模型就失效了。对于煤炭市场来说,考虑建模的方法、煤炭产业的周期等因素,预计模型失效时间粗略估计为3~5年。
应对模型失效这一问题,办法是每隔固定的一段时间,重新对模型的参数进行估计,重新估计参数的时间间隔不太长的话,变量不必重新选择,因为变量的总体关系变化一般不会太大。然后每隔更长的一个周期 (多年),对变量的参数也可以重新进行选择。
[1]李子奈,叶阿忠.高级应用计量经济学[M].北京:清华大学出版社,2012
[2]温渤,李大伟,汪寿阳.国际石油期货价格预测及风险度量研究[M].北京:科学出版社,2009
[3]高扬.大宗商品期货价格研究[M].北京:经济科学出版社,2011
[4]中国煤炭工业协会.2011中国煤炭工业发展研究报告[R].北京:中国经济出版社,2011
[5]魏毅,程跃,车永才.灰色理论在煤炭产品价格预测中的应用[J].中国煤炭,2006
[6]刘巍,陈昭.计量经济学软件EViews6.0建模方法与操作技巧[M].北京:机械工业出版社,2011
[7]高铁梅.计量经济分析方法与建模:EViews应用及实例 (第2版)[M].北京:清华大学出版社,2011
[8]李宏.中国煤炭运输:能力、消耗和价格[M].北京:中国市场出版社,2008
[9]张华明,赵国浩,焦斌.煤炭资源价格形成机制的政策体系研究[M].北京:冶金工业出版社,2011
